第1课时 菱形的性质与判定(1)课堂本
- 格式:ppt
- 大小:1.75 MB
- 文档页数:3




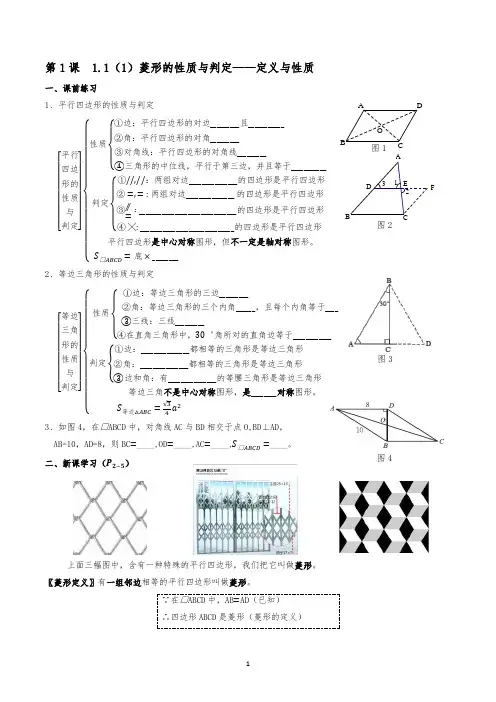




第一讲菱形的性质与判定(一)菱形的定义与性质1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.2.菱形的性质:(1)菱形的四条边都相等;(2)菱形的对角线互相垂直平分.并且平分一组对角。
(3)菱形既是中心对称图形,也是轴对称图形,对称轴是两条对角线所在的直线。
(4)菱形的面积计算:①菱形的面积等于底乘高②菱形的面积等于对角线乘积的一半;对角线互相垂直的四边形的面积都可以用两条对角线乘积的一半来进行计算3.菱形具有平行四边形的所有性质,应用菱形的性质可以进行计算和推理.典例分析:知识点1:利用菱形的性质求角的度数例1:如图,在菱形ABCD中,E,F分别是BC,CD上的点,∠B=∠EAF=60°,∠BAE=20°,求∠CEF的度数.知识点2:利用菱形的性质求线段长例2:(1)如图,已知菱形ABCD的对角线AC=8,BD=6,AC与BD相交于点O,求菱形ABCD 的周长与面积.(2)如图,P为菱形ABCD的对角线上一点,PE⊥AB于E,AP=5,AE=4,则点P到边AD 的距离等于_________.例2(2)图例2(3)图(3)如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.知识点3:利用菱形的对称性求最短距离例3:(1)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD 上一动点,则EP+FP的最小值为()A.1B.2C.3D.4例3(1)图例3(2)图(2)如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F 分别是AG、AD上的两个动点,则EF+ED的最小值是.知识点4:利用菱形的性质求面积例4:如图,菱形ABCD中,E是AB的中点,且DE丄AB,AE=2.求:(1)对角线AC,BD的长;(2)菱形ABCD的面积.知识点5:利用菱形的性质证明例5:(1)已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.①求证:AE=AF;②若∠B=60°,点E,F分别为BC和CD的中点,求证:△AEF为等边三角形.(2)如图,在菱形ABCD中,P是AB上的一个动点(不与A,B重合),连接DP交对角线AC于E,连接EB.求证:∠APD=∠EBC.(二)菱形的判定判定方法:1、定义法:有一组邻边相等的平行四边形叫做菱形2、对角线:①对角线互相垂直平分的四边形是菱形②对角线互相平分的平行四边形是菱形3、边:四条边都相等的四边形是菱形注:(1)菱形的判断可以从两个基本图形(四边形或平行四边形)考虑,进行证明.(2)菱形的性质定理和菱形的判定定理是互逆定理图文展示:典例分析:知识点6:利用定义判定菱形例6:已知:△ABC中,CD平分∠ACB交AB于D,DE∥AC交BC于E,DF∥BC 交AC于F.求证:四边形DECF是菱形.知识点7:利用“对角线互相垂直的平行四边形是菱形”判定菱形例7:如图:,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD,BC于点E,F,求证四边形BEDF是菱形.知识点8:利用“四边相等的四边形是菱形”判定菱形例8:如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点;求证:四边形EGFH是菱形.(三)菱形的性质与判定的综合应用例9:如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.例10:将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.(1)求证:△ABE≌△AD′F;(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.例11:如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.(1)求证:四边形ABCD是菱形;(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.例12:已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.夯实基础:1.下列性质中,菱形对角线不具有的是()A.对角线互相垂直B.对角线所在直线是对称轴C.对角线相等D.对角线互相平分2.已知▱ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB=BC;③AC平分∠BAD;④AO=DO.使得▱ABCD是菱形的条件有()A.1个B.2个C.3个D.4个3.如图,菱形ABCD的周长为8,高AE长为,则AC:BD=()A.1:2B.1:3C.1:D.1:第3题第4题4.菱形0BCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为.5.在菱形ABCD中,E,F分别是BC,CD上的点,若△AEF是等边三角形,且EF=AB,则∠BAD的度数是()A.100°B.105° C.110° D.120°6.已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为()A.12B.24C.48D.967.菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的周长为.第7题第8题第9题8.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为()A.24 cm2B.20 cm2C.16 cm2D.12 cm29.如图,菱形ABCD中,∠DAB=60°,DF⊥AB于点E,且DF=DC,连结PC,则∠DCF的度数为度.10.如图,菱形ABCD的对角线AC与BD相交于点O,已知AB=13cm,AC=24cm.(1)求:菱形ABCD的面积;(2)如过点D作DE⊥BC,垂足为E,求DE的长.11.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE,若∠E=50°,求∠BAO的大小.12.如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.(1)求证:AE=DF;(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.13.如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.(1)证明:四边形CFAE为菱形;(2)连接EF交AC于点O,若BC=10,求线段OF的长.14.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF ∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)证明四边形ADCF是菱形;(3)若AC=4,AB=5,求菱形ADCF的面积.15.如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.(1)求证:BE=CD;(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.16.已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.(1)求证:△AOE≌△COF;(2)若∠EOD=30°,求CE的长.。


第1讲 菱形的性质与判定 1.理解掌握菱形的概念性质及判定定理2.会用菱形的有关知识进行证明,会计算菱形的面积 知识点01 菱形的性质(1)菱形的定义:有一组邻边相等的平行四边形叫做菱形.(2)菱形的性质①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.(3)菱形的面积计算①利用平行四边形的面积公式. ②菱形面积12ab .(a 、b 是两条对角线的长度) 【知识拓展1】菱形的两条对角线长的比是32,面积是cm 12,则它的对角线的长分别是 cm , cm . (★)解答方法:∵ 设菱形的两条对角线的长分别为厘米厘米x x 3,2,∴ 122132=⋅⋅=x x S 菱形,∴ 解得舍去)(2,221-==x x , ∴ 对角线的长分别为cm cm 6,4。
答案:cm cm 6,4。
【总结方法】菱形的面积等于对角线乘积的一半。
【即学即练】两对角线分别是6cm 和8cm 的菱形面积是 _________ cm 2,周长是 _________ cm . (★) 解答方法:菱形面积是224286cm =÷⨯;∵菱形的对角线互相垂直平分,根据勾股定理可得,边长为5cm ,则周长是20cm . 知识精讲目标导航故答案为24,20.解答:24,20【知识拓展2】菱形的周长是它的高的8倍,则菱形较小的一个角为()(★★) A.60°B.45°C.30°D.15°解答方法:菱形的周长为边长的4倍,又∵菱形周长为高的8倍,∴AB=2AE,∵△ABE为直角三角形,∴∠ABC=30°.故选 C.答案:C【总结方法】本题考查了菱形各边长相等的性质,考查了直角三角形中的特殊角,本题中根据特殊角求得∠ABC=30°是解题的关键.【即学即练1】菱形的一条对角线与边长相等,则菱形中较小的内角是()(★★) A.60°B.15°C.30°D.90°解答方法:因为菱形的一条对角线与边长相等,所以该对角线和菱形的两边组成的是等边三角形,可得该菱形较小内角的度数是60°.解答:A【即学即练2】如果菱形的周长等于一条对角线长的4倍,那么这个菱形较小的一个内角等于度.(★★)解答方法:∵菱形的周长等于一条对角线长的4倍,∴AB=BD=AD,∴△ABD是等边三角形,∴∠A=60°.即这个菱形较小的一个内角等于60°.解答:60【知识拓展3】已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.求证:∠AFD=∠CBE. (★★)答案:证明:∵ 四边形ABCD 是菱形,∴ BCD CA CD CB ∠=平分,.∴ CE CE DCE BCE =∠=∠又.,∴ △BCE ≌△COB (SAS ).∴ ∠CBE=∠CDE .∵ 在菱形ABCD 中,AB ∥CD , ∴∠AFD=∠FDC∴ ∠AFD=∠CBE .【总结方法】通过菱形的基本性质可以得到三角形全等,进而推出对应角相等,然后利用平行内错角相等进行转化即可得到要证明的结论。
第1讲 菱形的性质与判定1. 理解菱形的概念;2. 探索并证明菱形的性质定理和判定定理,并能运用它们进行证明和计算;3. 通过经历菱形的性质定理和判定定理的探索过程,丰富学生的数学活动经验和体验,进一步培养和发展学生的合情推理能力;4. 通过菱形的性质定理和判定定理以及相关问题的证明和计算,进一步培养和发展学生的演绎推理能力。
知识点 1:菱形的性质菱形的定义:一组邻边相等的平行四边形叫做菱形。
※菱形的性质:(1)具有平行四边形的性质(2)且四条边都相等(3)两条对角线互相垂直平分,每一条对角线平分一组对角。
注意:菱形是轴对称图形,每条对角线所在的直线都是对称轴。
知识点2:菱形的面积菱形的面积等于两条对角线长的乘积的一半BD AC BD AC S S AOB Rt ABCD •=••⨯==∆2121212144菱形知识点3:菱形的判定※菱形的判别方法:一组邻边相等的平行四边形是菱形。
对角线互相垂直的平行四边形是菱形。
四条边都相等的四边形是菱形。
【题型1菱形的概念和性质】【典例1】如图,在菱形ABCD中,对角线AC,BD相交于点O,已知AC=10cm,BD=24cm,则△ABD的周长为()A.30cm B.36cm C.50cm D.52cm【变式1-1】如图,在菱形ABCD中,∠ABD=30°,则∠A的度数为()A.150°B.140°C.130°D.120°【变式1-2】在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定正确的是()A.AB=AD B.AC⊥BD C.∠DAC=∠BAC D.AC=BD 【变式1-3】如图,菱形ABCO中的顶点O,A的坐标分别为(0,0),,点C在x轴的正半轴上,则点B的坐标为()A.B.C.D.【典例2】(2022秋•绥化期末)下列不属于菱形性质的是()A.四条边都相等B.两条对角线相等C.两条对角线互相垂直D.每一条对角线平分一组对角【变式2-1】(2022秋•舞钢市期中)下列说法不正确的是()A.菱形的四条边都相等B.菱形的对角线相等C.菱形是轴对称图形D.菱形的对角线互相垂直【变式2-2】(2022春•兰陵县期末)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是()A.25°B.30°C.35°D.40°【变式2-3】(2022•赫章县模拟)如图,在平面直角坐标系中,四边形ABCD 为菱形,A,B两点的坐标分别是(4,0),(0,3),点C,D在坐标轴上,则菱形ABCD的周长等于()A.16B.20C.24D.26【典例3-1】(2021秋•榆林期末)如图,在菱形ABCD中,若AB=5,AC=8,则菱形ABCD的面积为()A.24B.20C.16D.12【典例3-2】(2022•文山州模拟)如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,DB=8,则点A到BC的距离为()A.B.6C.8D.(2021秋•深圳期末)已知菱形的两条对角线的长分别为6cm和8cm,【变式3-1】则这个菱形的面积是()A.20cm2B.24cm2C.48cm2D.100cm2【变式3-2】(2021秋•毕节市期末)如图,在菱形ABCD中,对角线AC与BD 相交于点O,且AC=6,DB=8,AE⊥BC于点E,则AE=()A.6B.8C.D.【题型2:菱形的判定】【典例4】依据所标识的数据,下列平行四边形一定为菱形的是()A.B.C.D.【变式4-1】在下列条件中,能够判定▱ABCD为菱形的是()A.AB=AC B.AC⊥BD C.AC⊥BC D.AC=BD【变式4-2】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO.添加下列条件,能判定四边形ABCD是菱形的是()A.AB=AD B.AC=BD C.∠ABC=90°D.AO=BO【变式4-3】要检验一张四边形的纸片是否为菱形,下列方案中可行的是()A.度量四个内角是否相等B.测量两条对角线是否相等C.测量两条对角线的交点到四个顶点的距离是否相等D.将这纸片分别沿两条对角线对折,看对角线两侧的部分是否每次都完全重合【典例5】(2022春•苍溪县期末)如图,在△AFC中,∠F AC=90°,B、E分别是FC、AB的中点,过点A作AD∥FC交FE的延长线于点D.(1)求证:BF=AD;(2)求证:四边形ABCD是菱形.【变式5-1】(2022秋•章丘区校级月考)已知:如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点F,E是AC的中点,过点A作AD∥BC,交FE的延长线于点D.(1)求证:四边形AFCD是平行四边形;(2)给△ABC添加一个条件,使得四边形AFCD是菱形.请证明你的结论.【变式5-2】(2022•天宁区校级一模)如图,在四边形ABCD中,AC与BD相交于点O.且AO=CO,点E在BD上,满足∠EAO=∠DCO.(1)求证:△AOE≌△COD;(2)若AB=BC,求证:四边形AECD是菱形.【题型3:菱形的性质与判定综合】【典例6】(2022•冷水滩区校级开学)如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于点D,交BC于点E,过点A作BC的平行线交ED于点F,连接AE,AF.(1)求证:四边形AECF是菱形;(2)若AB=10,∠ACB=30°,求菱形AECF的面积.【变式6-1】(2022秋•龙岗区期末)如图,在四边形ABCD中,AB∥CD,AD ∥BC,AC平分∠DAB,连接BD交AC于点O,过点C作CE⊥AB交AB延长线于点E.(1)求证:四边形ABCD为菱形;(2)若OA=4,OB=3,求CE的长.【变式6-2】(2022•新市区校级一模)如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE、CF.(1)求证:四边形AECF是菱形;(2)若,∠F AC=30°,∠B=45°,求AB的长.【变式6-3】(2022春•张家港市校级月考)如图,▱ABCD对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE,OE=CD.(1)求证:▱ABCD是菱形;(2)若AB=4,∠ABC=60°,求AE的长.1.(2022•河南)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E 为CD的中点.若OE=3,则菱形ABCD的周长为()A.6B.12C.24D.48 2.(2022•湘西州)如图,菱形ABCD的对角线AC、BD相交于点O,过点D 作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32,则CD的长为()A.4B.4C.8D.8 3.(2022•淄博)如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为()A.16B.6C.12D.30 4.(2022•甘肃)如图,菱形ABCD中,对角线AC与BD相交于点O,若AB =2cm,AC=4cm,则BD的长为cm.5.(2022•北京)如图,在▱ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.6.(2022•岳阳)如图,点E,F分别在▱ABCD的边AB,BC上,AE=CF,连接DE,DF.请从以下三个条件:①∠1=∠2;②DE=DF;③∠3=∠4中,选择一个合适的作为已知条件,使▱ABCD为菱形.(1)你添加的条件是(填序号);(2)添加了条件后,请证明▱ABCD为菱形.7.(2022•大连)如图,四边形ABCD是菱形,点E,F分别在AB,AD上,AE =AF.求证:CE=CF.8.(2022•广元)如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.(1)求证:四边形AECD为菱形;(2)若∠D=120°,DC=2,求△ABC的面积.9.(2022•凉山州)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD 的中点,过点A作AF∥BC交CE的延长线于点F.(1)求证:四边形ADBF是菱形;(2)若AB=8,菱形ADBF的面积为40.求AC的长.1.(2022•齐齐哈尔)如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是.(只需写出一个条件即可)2.(2021春•龙马潭区期末)如图,在菱形ABCD中,对角线AC,BD相交于点O,E是AB的中点,连结EO.若EO=2,则CD的长为()A.2B.3C.4D.5 3.(2022秋•丰城市校级期末)如图,菱形ABCD中对角线相交于点O,AB=AC,则∠ADB的度数是()A.30°B.40°C.50°D.60°4.(2022秋•南海区期中)如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的周长是()A.14cm B.16cm C.18cm D.20cm 5.(2021秋•建平县期末)如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的周长为()A.6B.8C.12D.16 6.(2022秋•碑林区校级期中)如图,已知菱形的两条对角线AC与BD长分别是12和16,则这个菱形的面积是()A.192B.48C.96D.40 7.(2022秋•三明期中)如图,在菱形ABCD中,AC交BD于点O,DE⊥BC 于点E,连接OE,若∠BCD=50°,则∠OED的度数是()A.25°B.30°C.35°D.20°9.(2022秋•浑南区期中)在下列条件中,能够判定四边形是菱形的是()A.两条对角线相等B.两条对角线互相垂直平分C.两条对角线互相垂直D.两条对角线相等且互相垂直10.(2022秋•二七区校级月考)如图▱ABCD的对角线AC和BD相交于点O,下列说法正确的是()A.若OB=OD,则▱ABCD是菱形B.若AC=BD,则▱ABCD是菱形C.若OA=OD,则▱ABCD是菱形D.若AC⊥BD,则▱ABCD是菱形11.(2022春•铁西区期末)已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC =60°,BC的垂直平分线分别交BC和AB于点D和点E,点F在DE的延长线上,且AF=CE.(1)∠BCE的度数为°.(2)求证:四边形ACEF是菱形.12.(2022春•长乐区期中)如图,▱ABCD的对角线AC,BD相交于点O,且AB=13,AO=12,BO=5.求证:▱ABCD是菱形.13.(2022秋•海淀区期中)如图,在△ABC中,∠ABC=90°,BD为△ABC的中线.BE∥DC,BE=DC,连接CE.(1)求证:四边形BDCE为菱形;(2)连接DE,若∠ACB=60°,BC=4,求DE的长.。