3.4.1基本不等式的证明

3.4.1基本不等式(1)一、学习目标1.了解基本不等式的证明过程，会用基本不等式证明一些简单的不等式；2.通过小组活动培养学生观察、联想的能力，并能体会出证明不等式的基本思想方法.二、教学重点、难点：基本不等式的证明.三、课前自学问题1： 把一物体放在天平的一个盘子上，在另一个盘子上放砝码使之平衡，称得物体质量为a ；后来发现天平制造的不精确，左右两臂长不相等（其他因素不计），那么a 并非物体的实际质量。

后来有人想到做第二次测量：把物体调换到天平的另一个盘上，此时，称得物体质量为b ，请思考：那么如何合理地表示物体的质量呢？简单的做法是，把两次称得物体的质量 “平均”一下,以2b a A +=表示物体的质量.这样做合理吗？问题2： 思考如何证明基本不等式 2b a ab +≤.问题3： 你能否根据下图给出基本不等式的几何解释？四、问题探究例1 设a ,b 为正数，证明下列不等式成立：（1）求证：2≥+b a a b ； （2）求证：21≥+aa .变式： (1)已知 m>0，求证：24624≥+m m ；(2)求证：)3(734>≥+-a a a .例2.(1)求证：2)2(222b a b a ab +≤+≤. (2) 若R b a ∈,，求证:ca bc ab c b a ++≥++222(3)已知：c b a ,,均为正数，求证：c b a cab b ac a bc ++≥++五、反馈小结 1已知a 、b 、c 都是正数，求证：（a ＋b ）（b ＋c ）（c ＋a ）≥８abc .2课本99练习 1,2,3,6.7课后作业：1.给出下列结论：（1）若0,0,x y >>则lg lg x y +≥（2）若0,x >则1cos 2cos x x +≥=（3）若0x <，则44x x +≤-=-（4）若0x <，则222x x -+>=其中正确的有2.证明下列不等式. ⑴求证：2)2(222b a b a +≤+；⑵22222-+≥+b a b a ；⑶设),0(,+∞∈b a ，求证：ab b a ab ≤+2.3.求证：⑴11122>++x x ；⑵22322>++x x .4．已知 a <b <c , x =))((a b b c --,y=2a c -,比较x ,y 的大小关系.5.某种产品的两种原料相继提价，因此，产品生产者决定根据这两种原料提价的百分比，对产品分两次提价，现在有三种提价方案：方案甲：第一次提价%p ，第二次体积%q ；方案乙：第一次提价%q ，第二次提价%p ； 方案丙：第一次提价%2q p +，第二次提价%2q p +. 其中0>>q p ，比较上述三种方案，哪一种提价少？哪一种提价多？6已知：a,b,c 是正数，且a+b+c=1. 求证：8)11)(11)(11(≥---c b a .。

3.4.1基本不等式课标要求：通过两个探究实例，引导学生从几何图形中获得两个基本不等式，了解基本不等式的几何背景，体会数形结合的思想。

在教学过程中，进一步提炼、完善基本不等式，并从代数角度给出不等式的证明，组织学生分析证明方法，加深对基本不等式的认识，提高逻辑推理论证能力。

结合课本的探究图形，引导学生进一步探究基本不等式的几何解释，强化数形结合的思想。

一、教学分析本节课是在系统的学习了不等关系和不等式性质，掌握了不等式性质的基础上展开的，作为重要的基本不等式之一,为后续的学习奠定基础。

要进一步了解不等式的性质及运用，研究最值问题，此时基本不等式是必不可缺的。

基本不等式在知识体系中起了承上启下的作用，同时在生活及生产实际中有着广泛的应用，因此它也是对学生进行情感价值观教育的好素材，所以基本不等式应重点研究。

二、教学目标1、知识与技能：(1) 师生共同探究基本不等式；(2) 了解基本不等式的代数、几何背景及基本不等式的证明；(3) 会简单运用基本不等式。

2、过程与方法：通过基本不等式的探索、发现，在知识发生、发展以及形成过程中培养学生观察、联想、归纳、分析、综合和逻辑推理的能力；遵循从特殊到一般的认知规律，让学生在实践中通过观察、尝试、分析、类比的方法导出基本不等式，培养学生数形结合的思维能力。

3、情感、态度与价值观：(1)培养学生举一反三的逻辑推理能力，并通过不等式的几何解释，丰富学生数形结合的想象力；(2) 通过具体的现实问题提出、分析与解决，激发学生探究的兴趣和欲望，树立学生求真的勇气和自信心，增强学生学好数学的心理体验，产生热爱数学的情感，体验在学习中获得成功的快乐。

三．重点难点重点：应用数形结合的思想理解不等式，并从不同角度探索不等式的证明过程。

难点：基本不等式等号成立条件及应用。

四、课时安排2课时五、教学方法：讨论法、演示法、启发法、练习法等六、教学设想（一）创设情景，提出问题；设计意图：数学教育必须基于学生的“数学现实”，现实情境问题是数学教学的平台，数学教师的任务之一就是帮助学生构造数学现实，并在此基础上发展他们的数学现实．基于此,设置如下情境:右图是在北京召开的第24届国际数学家大会的会标，会标是根据中国古代数学家赵爽的弦图设计的，颜色的明暗使它看上去像一个风车，代表中国人民热情好客。

3.4.1 基本不等式2ba ab +≤的证明在前两节课的研究当中，学生已掌握了一些简单的不等式及其应用，并能用不等式及不等式组抽象出实际问题中的不等量关系，掌握了不等式的一些简单性质与证明，研究了一元二次不等式及其解法，学习了二元一次不等式（组）与简单的线性规划问题.本节课的研究是前三大节学习的延续和拓展.另外，为基本不等式的应用垫定了坚实的基础，所以说，本节课是起到了承上启下的作用.教学目标：1.创设用代数与几何两方面背景，用数形结合的思想理解基本不等式；2.尝试让学生从不同角度探索基本不等式的证明过程；3.从基本不等式的证明过程进一步体会不等式证明的常用思路，即由条件到结论，或由结论到条件.教学重点：1.创设代数与几何背景，用数形结合的思想理解基本不等式；2.从不同角度探索基本不等式的证明过程；3.从基本不等式的证明过程进一步体会不等式证明的常用思路.教学难点：1.对基本不等式从不同角度的探索证明；2.通过基本不等式的证明过程体会分析法的证明思路.教学方法：应用观察、类比、归纳、逻辑分析、思考、合作交流、探究，得出基本不等式，实行启发、探究式教学并使用多媒体辅助.教学过程：本节课是通过让学生观察第２４届国际数学家大会的会标图案中隐含的相等关系与不等关系而引入的.通过度析得出基本不等式：2ba ab +≤，然后从三种角度对基本不等式展开证明及对基本不等式展开一些简单的应用,进而更深一层次地从理性角度建立不等观点.讲解过程中应作好点拨，利用几何背景，数形结合做好归纳总结、逻辑分析，并鼓励学生从理性角度去分析探索过程，进而更深层次理解基本不等式，鼓励学生对数学知识和方法获得过程的探索，同时也能激发学生的学习兴趣，一．引入新课由北京召开的第24届国际数学家大会的会标引入，请学生在这个图中找出一些相等关系或不等关系。

.通过直观情景导入有利于吸引学生的注意力，激发学生的学习热情，并增强学生的爱国主义热情由上图抽象出如下图形通过引导和学生间的合作交流的第一个不等式：一般地，对于任意实数a 、b ，我们有a 2+b 2≥2ab ，当且仅当a =b 时，等号成立.并由学生自己完成证明过程，老师做适当点评。

3.4 基本不等式: 2b a ab +≤(1) 学习目标：1.创设代数与几何背景,用数形结合的思想理解基本不等式；2.从不同角度探索基本不等式的证明过程;；3.从基本不等式的证明过程进一步体会不等式的常用思路.一、新课引入探究： 上图是在北京召开的第24届国际数学家大会的会标，会标是根据中国古代数学家赵爽的弦图设计的，颜色的明暗使它看上去像个风车，代表中国人民热情好客，你能在这个图中找出一写相等关系或不等关系吗？问题(1)：正方形的面积与四个直角三角形的面积之和有什么关系？你能证明这个关系吗?问题(2) ：正方形的面积与四个直角三角形的面积之和什么情况下相等？（或什么情况下取等号）结论：一般地，对于任意实数b a 、，都有 . 问题（3）：当0,0>>b a 时，是否可以用b a 、代替不等式中的b a 、？代替后是： ，你能给出证明吗？我们常把2b a +叫做正数b a 、的 ，把 叫做正数b a 、的几何平均数. 探究：如图，AB 是圆的直径，点C 是AB 上的一点，.,b BC a AC ==过点C 作垂直于AB 的弦DE 连接.BD AD 、你能利用这个图形，得出不等式2b a ab +≤的几何解释吗？总结：基本不等式2b a ab +≤使用应注意： 二、例题：例1. (1) 把36写成两个正数的积,当这 (2) 把18写成两个正数的和,当这两个正数取什么值时,它们的和最小? 两个正数取什么值时,它们的积最大?例2. (1)用篱笆围一个面积为2100m 的矩形菜园，问这个矩形的长、宽各为多少时，所用篱笆最短.最短的篱笆是多少？(2)一段长为m 36的篱笆围成一个矩形菜园，问这个矩形的长、宽各为多少时，菜园的面积最大.最大面积是多少？变式：一段长为m 30的篱笆围成一个一边靠墙的矩形菜园，墙长m 18，这个矩形的长、宽各为多少时，菜园的面积最大？最大面积是多少？例3. 某工厂要建造一个长方体形无盖 水池，其容积为34800m ，深为m 3.如果池底每平方米的造价为150元，池壁每平方米的造价为120元，怎样设计水池能使总造价最低？最低总造价是多少？变式：做一个体积为332m ，高为m 2的长方体纸盒，底面的长与宽取什么值时用纸最少？作业：1.0>x ，当x 取什么值，xx 1+的值最小？最小是多少？2. 已知直角三角形的面积等于50，两条直角边各为多少时，两条直角边的和最小，最小值是多少？3.已知矩形的周长为36，矩形绕它的一条边旋转形成一个圆柱，矩形的长、宽各为多少时，旋转形成的圆柱的侧面积最大？4.某单位建造一间背面靠墙的小房，地面面积为212m ，房屋正面每平方米的造价为1200元，房屋侧面每平方米的造价为800元，屋顶的造价为5800元.如果墙高为m 3，且不计房屋背面和地面的费用，问怎样设计房屋能使总造价最低？最低总造价是多少？5.已知()+∞∈,0b a 、，求证：2233ab b a b a +≥+.6．用 cm 20长的铁丝折成一个面积最大的矩形，应当怎样折？7.已知y x 、都是正数，求证：2≥+y x x y .8. 已知c b a 、、都是正数，求证：.8))()((abc c b c a b a ≥+++。

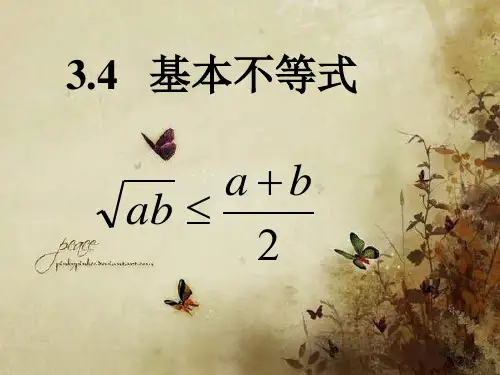
3.4 基本不等式ab ≤a ＋b2(a ≥0，b ≥0)3.4.1 基本不等式的证明1．理解基本不等式的内容及证明．(重点) 2．能运用基本不等式证明简单的不等式．(重点) 3．能用基本不等式求解简单的最大(小)值问题．(难点)[基础·初探]教材整理1 算术平均数与几何平均数 阅读教材P 96，完成下列问题．对于正数a ，b ，我们把a ＋b2称为a ，b 的算术平均数，ab 称为a ，b 的几何平均数．若两个正数a ，b 的算术平均数为2，几何平均数为2，则a ＝ ，b ＝ .【解析】由题意可知⎩⎪⎨⎪⎧a ＋b 2＝2，ab ＝2，∴⎩⎪⎨⎪⎧a ＋b ＝4，ab ＝4，∴a ＝2，b ＝2. 【答案】 2 2教材整理2 基本不等式阅读教材P97～P98，完成下列问题．如果a，b是正数，那么ab≤a＋b2(当且仅当a＝b时取“＝”)，我们把不等式ab≤a＋b2(a≥0，b≥0)称为基本不等式．判断(正确的打“√”，错误的打“×”)(1)对任意a，b∈R，都有a＋b≥2ab成立．()(2)不等式a2＋4≥4a成立的条件是a＝2.()【答案】(1)×(2)√[小组合作型]用基本不等式证明不等式已知a，b，c为不全相等的正数．(1)求证：a＋b＋c>ab＋bc＋ca；(2)求证：a2b＋b2c＋c2a≥a＋b＋c.【精彩点拨】(1)利用a＋b≥2ab，a＋c≥2ac，b＋c≥2bc求证；(2)利用a2b＋b≥2a2；b2c＋c≥2b2；c2a＋a≥2c2求证．【自主解答】(1)∵a>0，b>0，c>0，∴a＋b≥2ab，a＋c≥2ac，b＋c≥2bc.又a，b，c为不全相等的正数，∴a＋b＋c≥ab＋ac＋bc.又a，b，c互不相等，故等号不能同时取到， 所以a ＋b ＋c >ab ＋ac ＋bc . (2)∵a ，b ，c ，a 2b ，b 2c ，c 2a 均大于0， ∴a 2b ＋b ≥2a 2b ·b ＝2a ， 当且仅当a 2b ＝b 时等号成立． b 2c ＋c ≥2b 2c ·c ＝2b ， 当且仅当b 2c ＝c 时等号成立． c 2a ＋a ≥2c 2a ·a ＝2c ， 当且仅当c 2a ＝a 时等号成立．相加得a 2b ＋b ＋b 2c ＋c ＋c 2a ＋a ≥2a ＋2b ＋2c ， ∴a 2b ＋b 2c ＋c 2a ≥a ＋b ＋c .利用基本不等式证明不等式的条件要求：(1)利用基本不等式证明不等式，关键是所证不等式中必须有“和”或“积”式，通过将“和”式转化为“积”式或将“积”式转化为“和”式，从而达到放缩的效果.(2)注意多次运用基本不等式时等号能否取到.[再练一题]1．已知a ，b ，c ∈(0，＋∞)，且a ＋b ＋c ＝1. 求证：1a ＋1b ＋1c ≥9.【证明】 法一 ∵a ，b ，c ∈(0，＋∞)，且a ＋b ＋c ＝1，∴1a ＋1b ＋1c＝a ＋b ＋c a ＋a ＋b ＋c b ＋a ＋b ＋c c＝3＋⎝ ⎛⎭⎪⎫b a ＋a b ＋⎝ ⎛⎭⎪⎫c a ＋a c ＋⎝ ⎛⎭⎪⎫c b ＋b c ≥3＋2＋2＋2＝9.当且仅当a ＝b ＝c ＝13时等号成立．法二 ∵a ，b ，c ∈(0，＋∞)，且a ＋b ＋c ＝1， ∴1a ＋1b ＋1c ＝⎝ ⎛⎭⎪⎫1a ＋1b ＋1c (a ＋b ＋c )＝3＋⎝ ⎛⎭⎪⎫b a ＋a b ＋⎝ ⎛⎭⎪⎫c a ＋a c ＋⎝ ⎛⎭⎪⎫c b ＋a c ≥3＋2＋2＋2＝9，当且仅当a ＝b ＝c ＝13时等号成立．[探究共研型]应用基本不等式应注意的问题探究1 不等式“x ＋1x ≥2x ·1x ＝2”成立吗？为什么？【提示】 不成立．如当x <0时，x ＋1x <0，显然不成立．探究2 当x <0时，能否应用基本不等式求解，x ＋1x 的范围是多少？ 【提示】 可以，当x <0时，－x >0， ∴x ＋1x ＝－⎣⎢⎡⎦⎥⎤(－x )＋⎝ ⎛⎭⎪⎫－1x≤－2(－x )·1(－x )＝－2.当且仅当－x ＝－1x ，即x ＝－1时等号成立， ∴x ＋1x ∈(－∞，－2]．探究3当x≥0时，如何求“x＋1x＋1”的最小值？【提示】x＋1x＋1＝(x＋1)＋1x＋1－1≥2(x＋1)·1x＋1－1＝2－1＝1，当且仅当x＋1＝1x＋1，即x＝0时等号成立．求函数y＝(x＋5)(x＋2)x＋1(x>－1)的最小值，并求相应的x值．【精彩点拨】y＝(x＋5)(x＋2)x＋1――→变形y＝(x＋1)＋kx＋1＋b――――→基本不等式求最小值【自主解答】y＝(x＋5)(x＋2)x＋1＝(x＋1)2＋5(x＋1)＋4x＋1＝(x＋1)＋4x＋1＋5，∵x>－1，∴x＋1>0，∴y≥2(x＋1)·4x＋1＋5＝4＋5＝9.当且仅当x＋1＝4x＋1，即x＝1时，等号成立．∴函数y＝(x＋5)(x＋2)x＋1(x>－1)的最小值为9，此时x＝1.1．基本不等式使用的条件为“一正、二定、三相等”，三个条件缺一不可．在解题过程中，为了达到使用基本不等式的条件，往往需要通过配凑、裂项、转化、分离常数等变形手段，创设一个应用基本不等式的情境．2．应用基本不等式求函数最值，常见类型如下：(1)构造积为定值，利用基本不等式求最值；(2)构造和为定值，利用基本不等式求最值．[再练一题]2．(1)已知0<x <13，求函数y ＝x (1－3x )的最大值； (2)已知x >54，求函数y ＝4x －2＋14x －5的最小值.【导学号：92862095】【解】 (1)∵0<x <13，∴1－3x >0，∴y ＝x (1－3x )＝13·3x (1－3x )≤ 13⎣⎢⎡⎦⎥⎤3x ＋(1－3x )22＝112， 当且仅当x ＝16时，函数y ＝x (1－3x )取得最大值112. (2)∵x >54，∴4x －5>0， ∴y ＝4x －2＋14x －5＝4x －5＋14x －5＋3 ≥2(4x －5)·14x －5＋3＝5.当且仅当4x －5＝14x －5，即x ＝32时取等号．∴当x ＝32时，y 取最小值为5.1．a ＋1≥2a (a >0)中等号成立的条件是 ． 【解析】 等号成立的条件是两项相等，即a ＝1. 【答案】 a ＝12．函数f (x )＝2x ＋8x (x >0)有最小值为 ． 【解析】 2x ＋8x ≥22x ·8x＝8，当且仅当x ＝2时等号成立． 【答案】 83．已知x ，y 为正实数，且x ＋4y ＝1，则xy 的最大值为 .【导学号：92862096】【解析】 ∵x >0，y >0，∴1＝x ＋4y ≥24xy ＝4xy ， ∴xy ≤116，当且仅当x ＝12，y ＝18时，等号成立． ∴(xy )max ＝116. 【答案】 1164．设b >a >0，且a ＋b ＝1，则四个数12，2ab ，a 2＋b 2，b 中最大的是_ ． 【解析】 ∵b >a >0，∴a 2＋b 2>2ab . 又∵a ＋b ＝1，∴b >12.又b ＝b (b ＋a )＝b 2＋ab >b 2＋a 2， 故b 最大． 【答案】 b5．已知a ，b ，c ，d 都是正实数．求证：ad ＋bc bd ＋bc ＋adac ≥4.【证明】 ∵a ，b ，c ，d 都是正实数， ∴ad ＋bc bd ＋bc ＋ad ac ＝a b ＋c d ＋b a ＋d c ＝⎝ ⎛⎭⎪⎫b a ＋a b ＋⎝ ⎛⎭⎪⎫d c ＋c d ≥2b a ·ab ＋2d c ·cd ＝4.当且仅当a ＝b 且c ＝d 时取“＝”．。