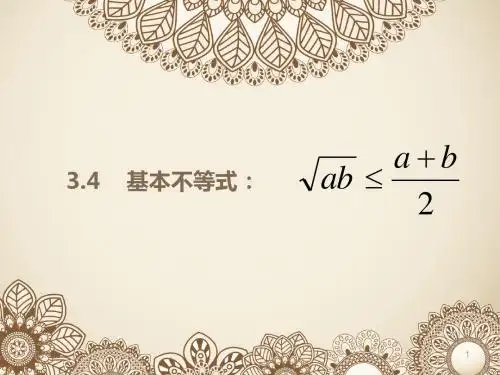当前位置：文档之家 › 基本不等式的证明ppt课件

基本不等式的证明ppt课件

  • 格式：ppt
  • 大小：519.50 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

基本不等式课件(共43张PPT)

基本不等式课件(共43张PPT)

02
基本不等式的证明方法
综合法证明基本不等式
利用已知的基本不等式推导
01
通过已知的不等式关系，结合不等式的性质（如传递性、可加
性等），推导出目标不等式。
构造辅助函数
02
根据不等式的特点，构造一个辅助函数，通过对辅助函数的分
析来证明原不等式。
利用数学归纳法
03
对于涉及自然数n的不等式，可以考虑使用数学归纳法进行证明。
分析法证明基本不等式
寻找反例
通过寻找反例来证明某个不等式不成 立，从而推导出原不等式。
利数，可以利用中间值定理 来证明存在某个点使得函数值满足给 定的不等式。
通过分析不等式在极限情况下的性质， 来证明原不等式。
归纳法证明基本不等式
第一数学归纳法
通过对n=1和n=k+1时的情况进行归纳假设和推导，来证 明对于所有正整数n，原不等式都成立。
拓展公式及其应用
要点一
幂平均不等式
对于正实数$a, b$和实数$p, q$，且$p < q$，有 $left(frac{a^p + b^p}{2}right)^{1/p} leq left(frac{a^q + b^q}{2}right)^{1/q}$，用于比较不同幂次的平均值大小。
要点二
切比雪夫不等式
算术-几何平均不等式（AM-GM不等式）：对于非负实数$a_1, a_2, ldots, a_n$，有 $frac{a_1 + a_2 + ldots + a_n}{n} geq sqrt[n]{a_1a_2ldots a_n}$，用于求解最值问题。
柯西-施瓦茨不等式（Cauchy-Schwarz不等式）：对于任意实数序列${a_i}$和${b_i}$，有 $left(sum_{i=1}^{n}a_i^2right)left(sum_{i=1}^{n}b_i^2right) geq left(sum_{i=1}^{n}a_ib_iright)^2$，用于证明与内积有关的不等式问题。

基本不等式的证明_课件

基本不等式的证明_课件
证：∵ a2 b2 2ab
b2 c2 2bc c2 a2 2ca 以上三式相加：2(a2 b2 c2 ) 2ab 2bc 2ca
当且仅当a=b=c时等号成立
∴ a2 b2 c2 ab bc ca
例3：1.已知a,b, c都是正数,
求证(a b)(b c)(c a) 8abc.
猜想：对任意两个正数a、b,
ab a b (a 0,b 0) 2
此不等式是可以证明的，而且证明方法有很多种。
证法1：a
2
b
ab
1 [( a )2 ( b)2 2 a b] 2
1 ( a b)2 0
2
当且仅当 a b 即 a b 时，取“ ”。
证法2：要证
ab a b 2
基本不等式
不等式的一些常用结论： 1、如果a b,则a - b 0,反之也成立; 如果a＜b,则a - b＜0,反之也成立; 如果a＝b,则a - b＝0,反之也成立; 2、a 2 0; | a | 0;
问题引入 ab
• 1、两个正数a，b的等差中项是__2___;
• 两个正数a，b的等比中项是___a_b_;
cos x
cos x
x 0 ，则 x 4 2 x 4 4
x
x
（4）若 x 0
2x 2x 2 2x 2x 2
其中正确的有 （3）,（4）
回顾小结：
1.基本不等式其应用条件； 2.不等式证明的三种常用方法； 3.利用基本不等式去证明其它不等式或求最值。
•2、对两个正数a,b， a b又叫做正数a与b的
___算__术__平___均_.数
2
ab •3、对两个正数a,b， 又叫做正数a与b的
___几__何__平___均_.数

基本不等式ppt课件

基本不等式ppt课件
对于任意实数a和b，$(a-b)^2 \geq 0$，即 $a^2 - 2ab + b^2 \geq 0$。
利用均值不等式证明
对于任意实数a和b，$a^2 + b^2 \geq 2ab$，即$(a-b)^2 \geq 0$。
利用导数证明
对于任意实数a和b，设f(x) = x^2 - 2x(a+b) + (a+b)^2，则f'(x) = 2x - 2(a+b) = 2(x-ab)，当x≥a+b时，f'(x) ≥0；当x ≤ a+b时， f'(x) ≤0。故f(x)在区间[a+b, +\infty)上单调 递增，在区间(-\infty, a+b]上单调递减。于 是有f(x) ≥ f(a+b) = a^2 - 2ab + b^2 ≥0 。
02
基本不等式的应用
几何意义
直线和圆
利用基本不等式可以判断直线和圆的 位置关系，以及求解圆中弦长等几何 问题。
面积和体积
利用基本不等式可以求解一些涉及面 积和体积的问题，例如在给定周长的 条件下，求矩形或立方体的最大面积 或体积等。
代数意义
方程
利用基本不等式可以求解一些涉及方程的问题，例如利用基本不等式求根，判 断方程解的个数等。
证明方法
利用代数公式和实数的性质进行 证明。
基本不等式的性质
非负性
对于任意实数a和b，总有$(a-b)^2 \geq 0$，即$a^2 - 2ab + b^2 \geq 0$。
等号成立条件
当且仅当a=b时，基本不等式取等号。
传递性
若a≥b，c≥d，则ac≥bd。
基本不等式的证明

高中数学基本不等式 PPT课件 图文

高中数学基本不等式 PPT课件 图文
2. 一段长为30 m的篱笆围成一个一边靠墙 的矩形菜园，墙长18 m，问这个矩形的长 、宽各为多少时，菜园的面积最大？最大 面积是多少？
谢谢！ 学妹给我打电话，说她又换工作了，这次是销售。电话里，她絮絮叨叨说着一年多来工作上的不如意，她说工作一点都不开心，找不到半点成就感。 末了，她问我：学姐，为什么想找一份 自己热 爱的工 作这么 难呢？ 我问她上一份工作干了多久，她说不到 三个月 ，做的 还是行 政助理 的工作 ，工作 内容枯 燥乏味 不说， 还特别 容易得 罪人， 实在不 是自己 的理想 型。 我又问了她前几份工作辞职的原因，结 果都是 大同小 异，不 是因为 工作乏 味，就 是同事 不好相 处，再 者就是 薪水太 低，发 展前景 堪忧。 粗略估计，这姑娘毕业不到一年，工作 却已经 换了四 五份， 还跨了 三个行 业。 但即使如此频繁的跳槽，她也仍然没有 找不到 自己满 意的工 作。 2 我问她，心目中理想型的工作是什么样 子的。 她说， 姐，你 知道苏 明玉吗 ？就是 《都挺 好》电 视剧里 的女老 大，我 就喜欢 她样子 的工作 ，有挑 战有成 就感， 有钱有 权，生 活自由 ，如果 给我那 样的工 作，我 会投入 我全部 的热情 。 听她说完，我尴尬的笑了笑。 其实每一个人都向往这样的成功，但这 姑娘却 本末倒 置了， 并不是 有了钱 有了权 有了成 就以后 才全力 以赴的 工作， 而是全 力以赴 工作， 投入了 自己的 全部以 后，才 有了地 位名望 钱财。 你要先投入，才会有收获，当你真正投 入做一 件事后 ，会明 白两件 事：首 先你会 明白， 把一件 事认认 真真做 好，所 获得的 收益远 大于同 时做很 多事； 你会明白，有人风风火火做各种事仍未 有回报 ，是因 为他们 从未投 入过。 从“做 了”到 “做” ，正如 “知道 ”到“ 懂得” 的距离 。 3 之前

3.4基本不等式(共37张PPT)

3.4基本不等式(共37张PPT)
式又有何最值呢？
，此时
16:23
19
练习：课本100页2,3,4
16:23
20
bc ac ab 7.已知 a, b, c R ，求证： 6. a b c
也可写成
ab ab (a 0, b 0) 2
当且仅当 a=b 时“＝”号成 立 此不等式称为基本不等式
9
如果a>0,b>0 ，用 a , b 分别代替a,b.我 们将得到什么结果？
ab ab (a 0, b 0) 2
算术平均数 几何平均数
16:23
10
ab 若a 0, b 0, 则 ab . 2
解：设矩形菜园的长为xm,宽为ym, 则2x+2y=36, 即x+y=18，矩形菜园的面积为xy m2 结论2：两个正数 和为定值，则积 有最大值. 当且仅当x=y,即x=9，y=9时等号成立。 因此，这个矩形的长为9m、宽为9m时，菜 园的面积最大，最大面积是81 m2 。
16:23 17
最值定理：若x、y皆为正数，则
若a 0, b 0, 则a b 2 ab .
a≥0，b≥0
( a b ) 0 其中a,b∈R？
2
a R， a 0
2
a, b R, (a b) 0
2
a, b R, a 2 b2 2ab
16:23 11
证明:当
时,
.
ab 证明:要证 ab ① 2
2x y 40
等号当且仅当
x y
时成立,此时
x y 10
因此,这个矩形的长和宽都是10m时,所用的篱笆 最短,最短为40m 结论1.两个正数积为定值，则和有最小值

《基本不等式》课件

《基本不等式》课件
《基本不等式》PPT课件
欢迎来到《基本不等式》PPT课件！在本次课程中，我们将深入探讨基本不等 式的概述、定义、性质以及证明方法。通过应用实例，我们将进一步理解如 何求最小值和进行定理证明。让我们一起展望本课件带来的新知识和启示！
基本不等式的概述
基本不等式是数学中的重要概念，用于比较两个数或者两个代数式的大小关 系。它是我们学习不等式的基石，掌握基本不等式对于解决更复杂的不等式 问题至关重要。
乘法性
将不等式的两边同时乘以 （或除以）相实数时， 不等式的符号反向。
基本不等式的证明方法
数学归纳法
通过归纳假设和递推关系，逐 步证明基本不等式的成立。
代数证明
将基本不等式转化为代数表达 式，通过代数运算和推导来证 明。
几何证明
借助几何图形和几何关系，通 过几何推理来证明基本不等式。
应用实例1：求最小值
基本不等式在求解数学问题时扮演着重要角色。通过对一些实际问题的分析，我们可以利用基本不等式的性质 来找到函数的最小值，有效地解决各种优化问题。
应用实例2：定理证明
基本不等式被广泛运用于数学定理的证明中。通过灵活应用基本不等式的定 义和性质，我们可以推导出一系列重要的数学结论和定理，拓展数学领域的 边界。
基本不等式的定义
基本不等式指的是一类具有特定形式的不等式，其中常见的包括平均数不等 式、均方根不等式和柯西-施瓦茨不等式。这些定义为我们解决各种数学问题 提供了强大的工具。
基本不等式的性质
单调性
基本不等式满足严格单调性， 即当其中的变量递增（或递 减）时，不等式的符号也相 应地改变。
加法性
将不等式的两边同时加上 （或减去）相同的实数时， 不等式的符号保持不变。
总结和展望

基本不等式的证明方法-PPT课件

基本不等式的证明方法-PPT课件
用综合法证明不等式的逻辑关系
A B1 B2 Bn B (已 知)(逐 步 推 演 不 等 式 成 立 的必 要 条 件)(结 论)
例1 已知a, b, c 0, 且不全相等,
求证a(b2 c2 ) b(c2 a2 ) c(a2 b2 ) 6abc
证明: b2 c2 2bc,a 0,a(b2 c2) 2abc c2 a2 2ac,b 0,b(c2 a2) 2abc a2 b2 2ab,c 0,c(a2 b2) 2abc
即证： 2 x1 x2 2 1 x1 x2 x1x2 ≥2 x1 x2 2 1 x1 x2 只要证： x1x2 ≥ 0
x1x2 ≥ 0 成立，故原不等式也成立。
3.(课本第 26 页习题 2.2 第 9 题)(分析法是解题的绝招) 已知 a 1 , b 1 ,求证: 1 ab a b
用分析法证“若A则B”这个命题的模式是: 为了证明命题B为真, 只需证明命题B1为真,从而有…… 只需证明命题B2为真,从而有……
…… 只需证明命题A为真. 而已知A为真,故B必真.
例3 求证 2 7 3 6
证明: 2 7和 3 6都是正数, 所以要证 2 7 3 6, 只需证( 2 7 )2 ( 3 6)2 , 展开得9 2 14 9 2 18, 只需证 14 18, 只需证14 18,14 18成立, 所以 2 7 3 6成立.
求证：lg a b ＋lg b c ＋lg c a ＞lga+lgb+lgc
2
2
2
证明: 要证 lg a b＋lg b c ＋lg c a ＞lga+lgb+lgc
2
2
2
只需证 lg a b b c c a ＞lgabc
222

基本不等式ppt 课件-

基本不等式ppt 课件-

解答：
AC=a，BC=b。过点 C作垂直于AB 的弦
可证△ACD∽△DCB，因而 CD= .由
DE，连接 AD，BD。你能利用这个图形，
于 CD 小于或等于圆的半径，用不等
得出基本不等式的几何解释吗?Leabharlann 式表示为+≤

显然，当且仅当点 C 与圆心重合，即
当a= 时，上述不等式的等号成立
2.2.4
分析：
(1) 矩形菜园的面积是矩形的两邻边之积，于是问题转
化为：矩形的邻边之积为定值，边长多大时周长最短。
(2) 矩形莱园的周长是矩形两邻边之和的 2倍，于是问
题转化为：矩形的邻边之和为定值，边长多大时面积
最大。
解答：
应用
例4：某工厂要建造一个长方体形无盖贮水池，
其容积为4 800 m³，深为3 m。如果池底每平
证明
证明方法一：作差法
证明方法二：借助完全平方公式
证明方法三：分析法
要证
≤
+

只要证 2 ≤ a+b
只要证 2 -a-b≤0
只要证 -( - )²≤0
只要证 ( − )²≥0
显然，最后一个成立，当且仅当a=b时，等号成
立
2.2.3
基本不等式的
几何解释
几何解释
如图：AB 是圆的直径，点C是AB 上一点
方米的造价为 150 元，池壁每平方米的造价为
解答：
设水池底的相邻两条边的边长分别为xm，ym，
水池的总价为z元，根据题意，有
120 元，那么怎样设计水池能使总造价最低?最
低总造价是多少?
由容积为4800m³，可得3xy=4 800，

基本不等式课件(共43张PPT)

基本不等式课件(共43张PPT)

重要不等式：一般地，对于任意实数a、b，总有
立
a2 b2≥2ab 当且仅当a=b时，等号成
适用范围： a,b∈R
文字叙述为: 两数的平方和不小于它们积的2倍.
如果a 0,b 0,我们用 a, b分别代替a,b, 可得到什么结论？
即： a b≥ ab (a 0,b 0) 2
通常我们把上式写作： ab≤ a b (a 0,b 0) 2
课堂练习： 已知 a，b，c∈{正实数}，且 a＋b＋c＝1.
求证：1a＋1b＋1c≥9.
解：证明：1a＋1b＋
1c ＝ a＋ab＋c ＋ a＋bb＋c ＋
a＋b＋c c
＝3＋
(ba＋ab)＋(ac＋ac)＋(bc＋bc)
≥3＋2＋2＋2＝9.
当且仅当a＝b＝c＝13时取等号．
小结 基本不等式 ab a b (a 0,b 0)
第三章 不等式
§3.4 基本不等式
这是2002年在北京召开的第24届国际数 学家大会会标．会标根据中国古代数学家赵爽 的弦图设计的，颜色的明暗使它看上去象一个 风车，代表中国人民热情好客。
D
a2 b2
b
G
F
A
a HE
探究１：
1、正方形ABCD的
面积S=＿a＿＿2 ＿＿b2
C ２、四个直角三角形的
例1.(1) 已知 x 0, 求证x 1 2, 并指出等号
成立的条件.
x
(2) 已知 ab 0, 寻找 a b 与2的大小关系, ba
并说明理由.
(3) 已知 ab 0, a b 能得到什么结论? 请说明理由. b a
[例 2] 若 a>b>1，P＝ lga·lgb，Q＝lga＋2 lgb，R＝lg(a＋2 b)， 试比较 P、Q、R 的大小．

高中数学必修五3.4.1 基本不等式的证明教学课件共18张PPT

高中数学必修五3.4.1 基本不等式的证明教学课件共18张PPT

C
S=ab
c=2(a+b)
积
和
物品放天平左边称砝码显示重量为a
物品放天平右边称砝码显示重量为b
2．主动引导 激发需求
物品放天平左边称砝码显示重量为a，放右边
称砝码显示重量为b，那么这个物品的实际重量是 多少？ M | l1 | l2 |
M
| l1 | l2 |
3．合作活动 提炼建模
活动 1 如图 5，请同学们先将一个正方形纸片沿它 们的对角线对折，然后用剪刀沿纸片对角线剪开，分成 两个全等的等腰直角三角形纸片． （课前请同学们预先 准备）
3．合作活动 提炼建模
活动 2 完成活动 1 后， 请同桌两位同学各取一个等
a b 腰直角三角形纸片（纸片的面积分别为 ， ） ，按如图 2 2 a +b 6 所示拼接成面积为 的多边形纸片． 2
3．合作活动 提炼建模
活动 3 完成活动 2 后，再请同桌两位同学合作，将
a +b 拼接成面积为 的多边形纸片按图 7 中虚线裁剪，去 2
普通高中课程标准实验教科书 数学（必修 5）
3.4 基本不等式的证明
1．自主阅读 提出问题
【阅读材料】五世纪，欧洲大地上贵族发起大规模 的圈地运动，其中有一种观点认为 “所圈矩形形状的地 的周长越长，则所圈地面积越大”． 你认同此观点吗？能从此观点中抽象出什么数学 问题吗？
A
a
D
b
b
B
a
ab ≥ ab ． a b ≥ 2 ab ， 2 ab 所以， 如果 a， b 是正数， 那么 ab ≤ （当 2
且仅当 a＝b 时取“＝”）． 当 a ≥ 0 ，b ≥ 0 时，这个不等式仍然成立．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
筒单地说就是“执果索因”.
9
说明：①分析法是“执果索因”，
步步寻求上一步成立的充分条件，它
论证“若A则B”这个
命题的模式是：为了证明命题B真，
只需要证明命题B1为真，从而有…… 只需要证明命题B2为真，从而又有……
……
只需要证明命题A为真
而已知A为真，故B必真
【变式】已知a,b,c都是互不相等的正数, 且abc=1,求证：
a b c111 abc
19
①教科书第93页习题3.4第1,2,3 ②《学习与评价》第11课时
20
（二）综合法——结合已知条件，再利用熟知的事 实或已经证明过的不等式作为基
础推导出所要求证的不等式。
（三）分析法——从- 求证的不等式出发，寻求使
它成立的充分条件，直至这些
条件都已具备，那么就可以断
定原不等式成立。
13
(三)定理：如果a,b是正数，那么
ab a b (当且仅当a b时取""号). 2
●两个非负数的算术平均数不小于它们的几何平均数.
★定理的变形公式：
(1)ab ( a b)2(当且仅当a b时取""号). 2
(2)a b 2 ab(当且仅当 a b时取""号).
(3)当ab 0时, a b 2(当且仅当a b时取""号). ba
(4)a2 b2 2ab(当且仅当 a b时取""号). 14
2
问题一：把一个物体放在天平的一个盘子上,在另一 个盘子上放砝码使天平平衡,称得物体的质量为a.如果 天平制造得不准确,天平的两臂长略有不同(其它因素 不计),那么并非实际质量.不过,我们可作第二次测量： 把物体调换到天平的另一盘上,此时称得物体的质量为 b.那么如何合理地表示物体的质量呢？
1.猜测： 物体的实际质量应为 a b
bd
ac
17
(一)证明不等式 例2.证明：若0<x<2,则 3x(6 3x) 3 【变式1】若0<x<2,证明： x(6 3x) 3 【变式2】若x>0,y>0且2x+y=1,证明： xy 1
8
18
(一)证明不等式 例3.已知a,b,c都是正数,且a+b+c=1,求证：
1 1 1 9 abc
n
a a a (当且仅当 1
2
时取"
n
"号).16
(一)证明不等式
例1.证明：
a2
1 a2
1
1(当且仅当a
0时取""号).
【变式1】已知a,b.c是不全相等的实数,证明：
a2 b2 c2 ab bc ac 【变式2】已知a,b.c,d都是正数,证明：
ad bc ab cd 4
4
【问题2】两个非负数的算术平均数与几何 平均数之间具有怎样的大小关系呢？ 1.试验： 2.猜测：ab a b (当且仅当a b时取""号).
2
3.证明：
5
●证明：如果a,b是正数，那么
ab a b (当且仅当a b时取""号). 2
证法一：
6
证明不等式的方法一：比较法
1. 依据： a b a b 0 ab ab0
(四)定理的几何解释
“半径不小于半弦”
15
(五)定理的拓广：
1.如果a,b,c是非负数，那么
3 abc a b c (当且仅当a b c时取""号). 3
三个非负数的算术平均数
不小于它们的几何平均数.
2.如果 a1,a2,,an 都是非负数,那么
n
a1a2 an
a1 a2 an
2.比较法（作差法）的解题步骤： 作差——变形——判断——结论
7
●证明：如果a,b是正数，那么
ab a b (当且仅当a b时取""号). 2
证法二：
8
证明不等式的方法二：分折法 证明不等式时，有时可以从求证的不
等式出发，分析使这个不等式成立的充分 条件，把证明不等式转化为判定这些充分 条件是否具备的问题，如果能够肯定这些 充分条件都已具备，那么就可以断定原不 等式成立，这种方法通常叫做分析法.
2.讨论：
2
3.提示： 应用力学原理求解 4.求解：
5.结论： 物体的实际质量应为 ab 3
(一)定义新概念
1.算术平均数：对于正数a,b,我们把 a 叫做a,b的算术平均数
2
b
2.几何平均数：对于正数a,b,我们把 ab
叫做a,b的算术平均数
(二)提出新问题
【问题2】两个非负数的算术平均数与几何 平均数之间具有怎样的大小关系呢？
高二数学(必修五)多媒体课件
3.4.1 基本不等式的证明
1
【问题1】
把一个物体放在天平的一个盘子上, 在另一个盘子上放砝码使天平平衡,称得 物体的质量为a.如果天平制造得不准确,天 平的两臂长略有不同(其它因素不计),那么 并非实际质量.不过,我们可作第二次测量： 把物体调换到天平的另一盘上,此时称得 物体的质量为b.那么如何合理地表示物体 的质量呢？
10
●证明：如果a,b是正数，那么
ab a b (当且仅当a b时取""号). 2
证法三：
11
证明不等式的方法三：综合法
利用某些已经证明过的不等式（如 基本不等式）和不等式的性质推导出所 要证明的不等式成立，这种证明方法通 常叫做综合法 。
筒单地说就是“由因导果”.
12
证明不等式的方法
（一）比较法—— 作差—变形—判号—结论。