横截面上切应力分布规律
- 格式:ppt
- 大小:2.28 MB
- 文档页数:3




材料力学笔记之——弯曲切应力、梁的强度条件横力弯曲的梁横截面上既有弯矩又有剪力,所以横截面上既有正应力又有切应力。
下面,讨论几种常见截面梁的弯曲切应力。
矩形截面从发生横力弯曲的梁上截取长度为dx的微段,该段梁上没有载荷作用,微段两侧截面上的剪力相等,但方向相反。
右侧截面上的弯矩相对左侧截面有增量,因为弯矩不等,因而两截面上的正应力也不相同。
对于狭长矩形截面,由于梁的侧面上无切应力,根据切应力互等定理,截面上两侧边各点处的切应力与边界相切,即与边界平行,梁发生对称弯曲,对称轴y轴上的切应力一定沿着y方向,在狭长截面上切应力沿宽度方向变化不大。
于是,关于横截面上切应力的分布规律,作以下假设:横截面上各点的切应力的方向都平行于剪力;切应力沿截面宽度均匀分布,即与中性轴平行的横线上各点的切应力大小相等。
截面高宽比大于2的情况下,以上述假定为基础得到的解与弹性理论的精确解相比,有足够的精确度。
根据切应力互等定理,横截面垂直的纵向截面上应存在与横截面上大小相等的切应力。
沿矩中性轴距离y的纵向面把微段截开,取纵向面下侧微元,受力如图所示。
左侧截面上正应力的合力为右侧截面上正应力的合力为显然这两个合力大小不等,纵向截面上必存在一个沿轴向的力使微段保持平衡,这个力为切应力的合力,这也证明了纵向截面上存在切应力,由于d x 是小量,则设纵向面的切应力均匀分布根据平衡条件即其中由切应力互等定理及剪力与弯矩之间的微分关系可得其中:b为截面上矩中性轴为y的横线的宽度,对于矩形截面为常数;I z为整个横截面对中性轴的惯性矩;S z*为横截面上矩中性轴为y的横线以外部分的面积对中性轴的静矩;F s为横截面上的剪力。
其中代入切应力计算公式切应力沿截面高度为抛物线分布,当y=0时,即中性轴处有截面上的最大切应力角应变为可见角应变大小沿截面高度也为抛物线分布,此时横力弯曲时横截面翘曲形状如下图,验证了横力弯曲变形不满足平面假设。
剪力不变的横力弯曲,相邻横截面上的切应力相同,翘曲程度也相同,纵向纤维的长度不因截面翘曲而改变,因此不会引起附加的正应力。

材料力学第三章答案材料力学第三章答案【篇一:材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( a )a ②③对b①③对c①②对d 全对7.扭转切应力公式?mnp?i?适用于(d)杆件。
pa 任意杆件;b 任意实心杆件;c 任意材料的圆截面;d 线弹性材料的圆截面。
9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的( d a 2倍; b 4倍; c 8倍; d 16倍。
三、计算题1.试用截面法求出图示圆轴各段内的扭矩t,并作扭矩图2.图示圆轴上作用有四个外力偶矩me1 =1kn/m, me2 =0.6kn/m,)me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图;⑵若me1与me2的作用位置互换,扭矩图有何变化?(1)(2)解:me1与me2的作用位置互换后,最大扭矩变小。
3.如图所示的空心圆轴,外径d=100㎜,内径d=80㎜,m=6kn/m,m=4kn/m.请绘出轴的扭矩图,并求出最大剪应力解:扭矩图如上,则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜,l=500tr4?103?50?103ip5.8?104.图示圆形截面轴的抗扭刚度为g ip,每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二:《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动,转速n?200r/min,轴上装有五个轮子,主动轮ii输入的功率为60kw,从动轮,i,iii,iv,v依次输出18kw,12kw,22kw和8kw。

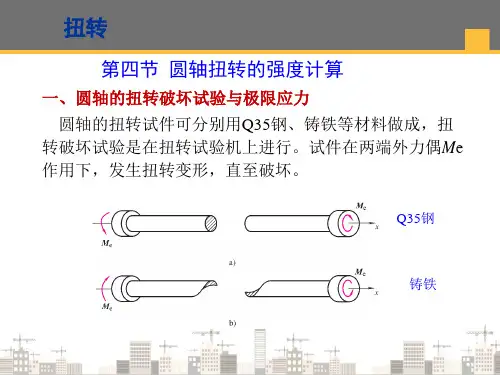
一、横截面上的切应力实心圆截面杆和非薄壁的空心圆截面杆受扭转时,我们没有理由认为它们在横截面上的切应力象薄壁圆筒中那样沿半径均匀分布导出这类杆件横截面上切应力计算公式,关键就在于确定切应力在横截面上的变化规律。
即横截面上距圆心τp任意一点处的切应力p与p的关系为了解决这个问题,首先观察圆截面杆受扭时表面的变形情况,据此做出内部变形假设,推断出杆件内任意半径p处圆柱表面上的切应变γp,即γp与p的几何关系利用切应力与切应变之间的物理关系,再利用静力学关系求出横截面上任一点处切应力τp的计算公式实验表明:等直圆杆受扭时原来画在表面上的圆周线只是绕杆的轴线转动,其大小和形状均不变,而且在小变形情况下,圆周线之间的纵向距离也不变图8-56扭转时的平面假设:等直圆杆受扭时它的横截面如同刚性圆盘那样绕杆轴线转动显然这就意味着:等直圆杆受扭时,其截面上任一根沿半径的直线仍保持为直线,只是绕圆心旋转了一个角度φ图8-57现从等直圆杆中取出长为dx的一个微段,从几何、物理、静力学三个方面来具体分析圆杆受扭时的横截面上的应力图8-581.几何方面小变形条件下dφ为dx长度内半径的转角,γ为单元体的角应变图8-59或因为dφ和dx是一定的,故越靠近截面中心即半径R越小,角应变γ也越小且γ与R成正比例(或线性关系)由平面假设:对同一截面上各点θ表示扭转角沿轴长的变化率,称为单位扭转角,在同一截面上其为常数所以截面上任一点的切应力与该点到轴心的距离p成正比p为圆截面上任一点到轴心距离,R为圆轴半径图8-60上式为切应力的变化规律2.物理方面(材料在线性弹性范围内工作)由剪切胡克定律由于G和为常数,所以上式表明受扭等直圆杆在线性弹性范围内工作时,横截面上的切应力在同一半径p 的圆周上各点处大小相同,但它们随p做线性变化同一横截面上的最大切应力在横截面的边缘处。
这些切应力的方向均垂直于各自所对应的半径,指向与扭矩对应3.静力学方面前面已找出了受扭等直圆杆横截面上的切应力τp随p变化的规律,但还没有把与扭矩T联系起来。


第18讲教学方案——弯曲切应力、弯曲强度条件§7-3 弯曲切应力梁受横弯曲时,虽然横截面上既有正应力σ,又有剪应力 τ。
但一般情况下,剪应力对梁的强度和变形的影响属于次要因素,因此对由剪力引起的剪应力,不再用变形、物理和静力关系进行推导,而是在承认正应力公式(6-2)仍然适用的基础上,假定剪应力在横截面上的分布规律,然后根据平衡条件导出剪应力的计算公式。
1.矩形截面梁对于图6-5所示的矩形截面梁,横截面上作用剪力Q 。
现分析距中性轴z 为y 的横线1aa 上的剪应力分布情况。
根据剪应力成对定理,横线1aa 两端的剪应力必与截面两侧边相切,即与剪力Q 的方向一致。
由于对称的关系,横线1aa 中点处的剪应力也必与Q 的方向相同。
根据这三点剪应力的方向,可以设想1aa 线上各点剪应力的方向皆平行于剪力Q 。
又因截面高度h 大于宽度b ,剪应力的数值沿横线1aa 不可能有太大变化,可以认为是均匀分布的。
基于上述分析,可作如下假设:1)横截面上任一点处的剪应力方向均平行于剪力 Q 。
2)剪应力沿截面宽度均匀分布。
基于上述假定得到的解,与精确解相比有足够的精确度。
从图6-6a 的横弯梁中截出dx 微段,其左右截面上的内力如图6-6b 所示。
梁的横截面尺寸如图6-6c 所示,现欲求距中性轴z 为y 的横线1aa 处的剪应力 τ。
过1aa 用平行于中性层的纵截面11cc aa 自dx 微段中截出一微块(图6-6d )。
根据剪应力成对定理,微块的纵截面上存在均匀分布的剪应力 τ'。
微块左右侧面上正应力的合力分别为1N 和2N ,其中*1I 1**z zAzA S I M dA I My dA N ===⎰⎰σ (a ) *1II 2)()(**z z Az A S I dM M dA I y dM M dA N +=+==⎰⎰σ (b)式中,*A 为微块的侧面面积,)(II I σσ为面积*A 中距中性轴为 1y 处的正应力,⎰=*1*A z dA y S 。
材料力学(应力应变部分)→规定载荷作用下,强度要求,就是指构件应有足够的抵抗破坏的能力。
刚度要求,就是指构件应有足够的抵抗变形的能力。
→变形的基本假设:连续性假设,均匀性假设,各向同性假设。
→沿不同方向力学性能不同的材料,称为各向异性材料,如木材、胶合板和某些人工合成材料。
→ 分布力 表面力集中力(火车轮对钢轨压力,滚珠轴承对轴的反作用力) 体积力是连续分布于物体内各点的力,例如物体的自重和惯性力等。
→动载荷,静载荷→应力p 应分解为正应力σ ,切应力τ 。
→应力单位pa ,1pa=1N/m 2;常用Mpa ,1Mpa=106pa 。
第二章 拉伸、压缩与剪切2.2 轴向拉伸或压缩时横截面上的内力和应力→习惯上,把拉伸的轴力规定为正,压缩时的轴力规定为负。
→用横截面上的应力来度量杆件的受力程度。
→F N =σA ;σ(x)=F N (x)/A(x)2.3 直杆轴向拉伸或压缩时斜截面上的内力和应力 α轴向拉伸(压缩)时,在杆件的横截面上,正应力为最大值;在与杆件轴线成45°的斜截面上,切应力为最大值。
最大切应力在数值上等于最大正应力的二分之一。
此外,α=90°时,σα=τα=0 ,这表示在平行于杆件轴线的纵向截面上无任何应力。
(应力,p=F/A ,45°斜截面上,力→√22,面积→√22。
) 2.7 安全因数许用应力和安全因数的数值,可以在有关部门的一些规范中查到。
目前一般机械制造中,在静载的情况下,对塑性材料可取n s =1.2~2.5。
脆性材料均匀性较差,且断裂突然发生,有更大的危险性,所以取n b =2~3.5,甚至取到3~9。
2.8 轴向拉伸或压缩时的变形→胡克定律,当应力不超过材料的比例极限时,应力与应变成正比。
σ=Eε ,弹性模量E 的值随材料而不同。
∆l l=ε=σE =F AE ;∆l =FLAE即,对长度相同,受力相等的杆件,有EA 越大则变形Δl越小,所以称EA 为杆件的抗拉/压刚度。
第三章杆件横截面上的应力应变分析利用截面法可以确定静定问题中的杆件横截面上的内力分量,但内力分量只是横截面上连续分布内力系的简化结果,仅根据内力并不能判断杆件是否有足够的强度。
如用同一种材料制成粗细不同的两根杆,在相同的拉力作用下,两杆的轴力是相同的,当拉力增大时,细杆必定先被拉断。
这说明拉杆的强度不仅与轴力大小有关,还与横截面面积有关,因此还必须引入内力集度的概,即应力的概念。
本章在此基础上分别讨论了杆件在拉压、扭转和弯曲三种基本变形和组合变形下横截面上应力的分布规律,导出了应力计算公式,为后面对杆件进行强度计算打下了基础。
第一节应力、应变及其相互关系一、正应力、剪应力观察图3-1a所示受力杆件,在截面上围绕K点取微小面积,其上作用有微内力,于是在上内力的平均集度为:(3-1)亦称为面积上的平均应力。
一般来说截面上的内力并不均匀分布,因此平均应力随所取ΔA的不同而变化。
当ΔA趋向于零时,的大小方向都将逐渐趋于某一极限。
(3-2)式中,p称为K点的应力,它反映内力系在K点的强弱程度。
p是一个矢量,一般说既不与截面垂直,也不与截面相切。
通常将其分解为垂直于截面的应力分量和相切于截面的应力分量(图3-1b)。
称为正应力,称为切应力。
在国际单位制中,应力的单位是牛顿/米2(N/M2),称为帕斯卡,简称帕(Pa)。
由于这个单位太小,通常使用兆帕(MPa),1MPa = 106Pa。
二、正应变、切应变杆件在外力作用下,其尺寸或几何形状将发生变化。
若围绕受力弹性体中任意点截取一个微小正六面体(当六面体的边长趋于无限小时称为单元体),六面体的棱边边长分别为Δx 、Δy 、Δz (图3-2 )。
把该六面体投影到xy平面(图3-2b)。
变形后,六面体的边长和棱边夹角都将发生变化(图3-2c)。
变形前长为Δx的线段MN,变形后长度为Δx+Δs。
相对变形(3-3)表示线段MN单位长度的平均伸长或缩短,称为平均应变。
当Δx趋向于零,即点N趋向于M点时,其极限为(3-4)式中,ε称为M点沿x方向的线应变或正应变,ε为无量纲量。
绪论单元测试1.在下列各工程材料中,()不可应用各向同性假设。
A:玻璃B: 松木C:铸铜D:铸铁答案:B2.根据均匀性假设,可认为构件的()在各处相等。
A:应力B:弹性常数C:位移D:应变答案:B3.研究变形体构件的平衡时,应按照变形后的尺寸计算。
A:对B:错答案:B4.小变形假设认为()。
A:构件不变形B:构件不破坏C:构件仅发生弹性变形D:构件的变形远小于其原始几何尺寸答案:D5.各向同性假设认为,材料沿各个方向具有相同的()。
A:力学性质B:位移C:内力D:变形答案:A6.下列不属于杆件变形基本形式的是()。
A:挤压B:扭转C:轴向拉伸(压缩)D:弯曲E:剪切答案:A7.构件的强度、刚度和稳定性()。
A:与上述两者均无关B:与上述两者均有关C:与构件的形状尺寸有关D:与材料的力学性质有关答案:B8.材料力学研究的对象几何特征是()。
A:块体B:杆件C:板壳D:构件答案:B9.材料力学的三个基本假设是()。
A:各向同性、连续性和弹性假设B:弹性、小变形和平面假设C:各向同性、连续性和均匀性假设D:弹性、均匀性和平面假设答案:C10.下列结论中正确的是()。
A:材料力学主要研究各种材料的力学问题B:材料力学主要研究各种材料的力学性质C:材料力学主要研究各种材料中力与材料的关系D:材料力学主要研究杆件受力后变形与破坏的规律答案:D第一章测试1.结构中有三根拉压杆,设由这三根杆的强度条件确定的结构许用荷载分别为,且,则结构的实际许可荷载为()。
A:B:C:D:答案:A2.图示拉伸(压缩)杆1-1截面的轴力为()。
A:B:C:D:答案:C3.用截面法求一水平杆某截面的内力时,是对()建立平衡方程求解的。
A:整个杆B:该截面右段C:该截面左段D:该截面左段或右段答案:D4.一般而言,我们采用材料的强度极限指标作为极限应力。
A:错B:对答案:A5.轴向拉伸杆,正应力最大的截面和切应力最大的截面()。
A:分别是横截面、45°斜截面B:都是45°斜截面C:都是横截面D:分别是45°斜截面、横截面答案:A6.轴向拉伸(压缩)作用下,杆件破坏一定发生在横截面上。