五年级数学组合图形面积练习试题

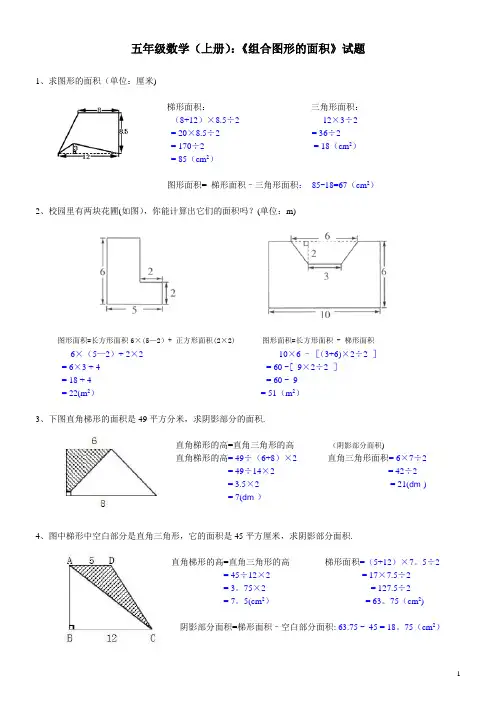
五年级数学（上册）：《组合图形的面积》试题1、求图形的面积(单位：厘米)梯形面积：三角形面积：（8+12）×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18（cm2）= 85（cm2）图形面积= 梯形面积–三角形面积：85-18=67（cm2）2、校园里有两块花圃(如图)，你能计算出它们的面积吗?(单位：m)图形面积=长方形面积6×（5-2）+ 正方形面积（2×2）图形面积=长方形面积 - 梯形面积6×（5-2）+ 2×2 10×6 –[（3+6）×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22（m2）= 51（m2）3、下图直角梯形的面积是49平方分米，求阴影部分的面积。

直角梯形的高=直角三角形的高（阴影部分面积）直角梯形的高= 49÷（6+8）×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21（dm²）= 7（dm²）4、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。

直角梯形的高=直角三角形的高梯形面积=（5+12）×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5（cm2）= 63.75（cm2）阴影部分面积=梯形面积–空白部分面积：63.75 - 45 = 18.75（cm2）5、阴影部分面积是40平方米，求空白部分面积。

（单位：米）梯形的高=三角形的高（阴影部分三角形）梯形面积=（6+10）×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8（m2）= 64（m2）空白部分面积=梯形面积–阴影部分面积：64–40 = 24（m2）6、如图，平行四边形面积240平方厘米，求阴影部分面积。

五年级数学（上册）：《组合图形的面积》试题1、求图形的面积（单位：厘米)梯形面积：三角形面积：（8+12）×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18（cm2）= 85（cm2）图形面积= 梯形面积–三角形面积：85-18=67（cm2）2、校园里有两块花圃(如图），你能计算出它们的面积吗？(单位：m)图形面积=长方形面积6×(5—2）+ 正方形面积(2×2) 图形面积=长方形面积 - 梯形面积6×（5—2）+ 2×2 10×6 –［（3+6)×2÷2 ］= 6×3 + 4 = 60 -[ 9×2÷2 ］= 18 + 4 = 60 - 9= 22(m2）= 51（m2）3、下图直角梯形的面积是49平方分米，求阴影部分的面积.直角梯形的高=直角三角形的高（阴影部分面积)直角梯形的高= 49÷（6+8）×2 直角三角形面积= 6×7÷2= 49÷14×2 = 42÷2= 3.5×2 = 21(dm²)= 7(dm²）4、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积.直角梯形的高=直角三角形的高梯形面积=（5+12）×7。

5÷2= 45÷12×2= 17×7.5÷2= 3。

75×2 = 127.5÷2= 7。

5(cm2）= 63。

75（cm2)阴影部分面积=梯形面积–空白部分面积: 63.75 - 45 = 18。

75（cm2）5、阴影部分面积是40平方米,求空白部分面积.（单位:米）梯形的高=三角形的高（阴影部分三角形）梯形面积=（6+10)×8÷2= 40÷10×2 = 16×8÷2= 4×2 = 128÷2= 8（m2）= 64（m2)空白部分面积=梯形面积–阴影部分面积: 64–40 = 24(m2）6、如图，平行四边形面积240平方厘米，求阴影部分面积.梯形的下底=平行四边形的底梯形面积=（15+20）×12÷2= 240÷12 = 35×12÷2= 20(cm）= 420÷2= 210（cm2)阴影部分面积= 平行四边形面积–梯形面积: 240–210 = 30(cm2) 7、下图ABCD是梯形,它的面积是140平方厘米，已知AB＝15厘米，DC＝5厘米。

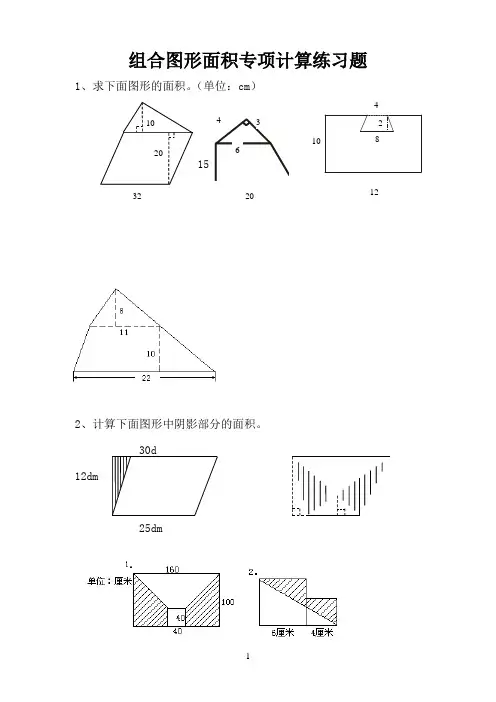
组合图形面积专项计算练习题1、求下面图形的面积。

（单位：cm ）2、计算下面图形中阴影部分的面积。

30d12dm25dm3、求下列阴影部分的面积。

②已知S 平＝48dm 2，求S 阴。

③已知：阴影部分的面积为24④求S 阴。

平方厘米，求梯形的面积。

4、求下面各图形的面积。

（单位：分米）16cm12cm 8dm8dm5、“实践操作”显身手：6、如右图所示，平行四边形的面积是48平方厘米，求阴影部分的面积。

7、如右图所示，梯形中阴影部分的面积是150平方厘米，求梯形的面积16cm2、求下面图形的面积。

25组合图形是由两个或两个以上的简单的几何图形组合而成的。

组合的形式分为两种：一是拼合组合，二是重叠组合。

由于组合图形具有条件相等的特点，往往使得问题的解决无从下手。

要正确解答组合图形的面积，应该注意以下几点：1．切实掌握有关简单图形的概念、公式，牢固建立空间观念；2．仔细观察，认真思考，看清所求图形是由哪几个基本图形组合而成的；3．适当采用增加辅助线等方法帮助解题；4．采用割、补、分解、代换等方法，可将复杂问题变得简单。

一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？1．求四边形ABCD的面积。

（单位：厘米）2．已知正方形ABCD的边长是7厘米，求正方形EFGH的面积。

3．有一个梯形，它的上底是5厘米，下底7厘米。

如果只把上底增加3厘米，那么面积就增加4.5平方厘米。

求原来梯形的面积。

正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

1．（如下图）已知大正方形的边长是12厘米，求中间最小正方形的面积。

2．正图长方形ABCD的面积是16平方厘米，E、F都是所在边的中点，求三角形AEF的面积。

3．求下图长方形ABCD的面积（单位：厘米）。

四边形ABCD和四边形DEFG都是正方形，已知三角形AFH的面积是7平方厘米。

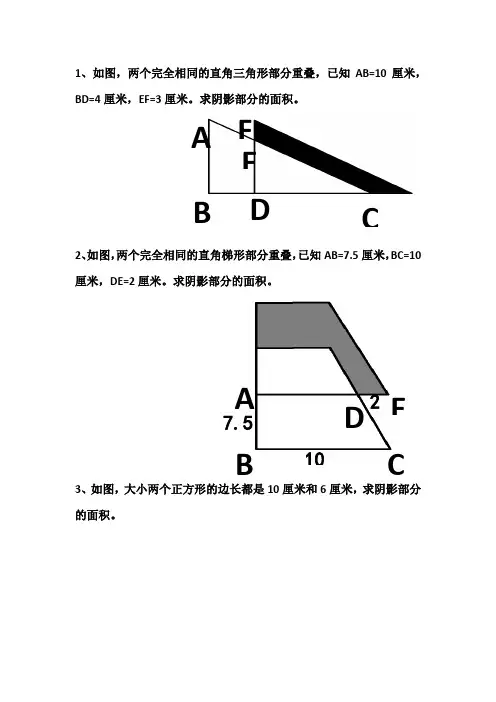
1、如图，两个完全相同的直角三角形部分重叠，已知AB=10厘米，BD=4厘米，EF=3厘米。

求阴影部分的面积。

2、如图，两个完全相同的直角梯形部分重叠，已知AB=7.5厘米，BC=10厘米，DE=2厘米。

求阴影部分的面积。

3、如图，大小两个正方形的边长都是10厘米和6厘米，求阴影部分的面积。

ABCDEFADEBC107.524、如图，大小两个正方形的边长都是10厘米和6厘米，求阴影部分的面积。

5、如图，由长方形ABCD 和直角梯形BEFC 组成，其中阴影部分的面积是36.5平方厘米，CD 是5厘米。

求长方形ABCD 的面积。

6、如图，平行四边形ABCD 的底BC 长12厘米，线段EF 长8.3厘米，求图中阴影部分的面积总和是多少平方厘米？ABCDEFABCDFEG7、如图，梯形上底长5.4厘米，下底长8.6厘米，高长4厘米，求三角形甲的面积比三角形乙的面积小多少平方厘米？8、如图，ABCD 是长方形，AB=8厘米，BC=6厘米，三角形ABF 的面积比三角形DEF 的面积大12平方厘米，求DE 长多少厘米？9、如图，平行四边形ABCD 的底BC 长10厘米，直角三角形FBC 的直角边FC 长8厘米。

已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。

求EF 的长度。

甲乙ABCDEF8681010、如图，△ABC 和△DCB 都是直角三角形，已知AB=3.4厘米，BC=7.2厘米，且甲比乙的面积大3.6平方厘米，求CD 的长。

11、如图，CA=AB=4厘米，三角形ABE 的面积比三角形CDE 的面积小2平方厘米，求CD 的长。

12、如图，甲的面积比乙的面积大36平方厘米，已知AB 长8厘米，BC 长12厘米，CD 长6厘米，求DE 的长。

ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图，D 是AC 的中点，E 、F 是BC 边上的三等分点，已知阴影部分的面积为20平方厘米，求三角形ABC 的面积。

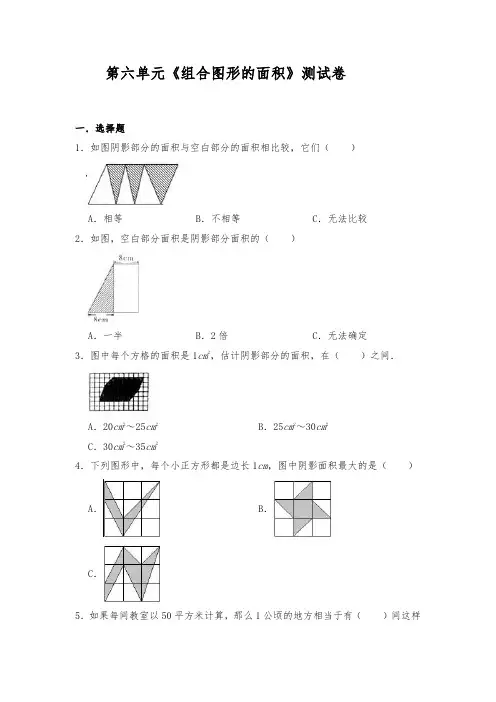
第六单元《组合图形的面积》测试卷一．选择题1．如图阴影部分的面积与空白部分的面积相比较，它们（）A．相等B．不相等C．无法比较2．如图，空白部分面积是阴影部分面积的（）A．一半B．2倍C．无法确定3．图中每个方格的面积是1cm2，估计阴影部分的面积，在（）之间．A．20cm2～25cm2B．25cm2～30cm2C．30cm2～35cm24．下列图形中，每个小正方形都是边长1cm，图中阴影面积最大的是（）A．B．C．5．如果每间教室以50平方米计算，那么1公顷的地方相当于有（）间这样A．20 B．200 C．2000 D．506．北京故宫的占地面积是720000平方米，合（）公顷。

A．72 B．720 C．72007．平方千米和公顷之间的进率是（）A．10 B．100 C．1000 D．100008．乐乐在计算如图中树叶的面积时作了一些标记。

如果每个方格的面积是1平方厘米，这片树叶的面积大约是（）平方厘米。

A．22 B．40 C．70二．填空题9．如图中阴影部分的面积大约是cm2（每个小格是1cm2）．10．把两个完全一样的正方体拼成一个长方体，拼成的长方体的表面积是原来两个正方体表面积和的．11．如图，大小两个正方形拼在一起，阴影部分面积为28平方厘米，小正方形边长为4厘米，则图中空白部分的面积是平方厘米．12．2公顷= 平方米 90000平方米= 公顷17平方千米= 公顷 400公顷= 平方千米13．一个风景区的占地面积是4平方千米50公顷，合起来是公顷，也就是平方米。

14．如图，AB＝BC＝CD＝4厘米，DF＝3厘米，则阴影部分的面积是平方15．用方格纸估计一个不规则图形的面积时，数出这个图形一共包含58个整格和26个不满整格．如果每个小方格表示1平方分米，这个图形的实际面积比平方分米大一些，比平方分米小一些．16．一个零件的横截面如图（单位：厘米），它的面积是．三．判断题17．一间教室的面积约为50平方米，那么200间这样的教室总面积约为1公顷．（）18．3滴水有1升．（）19．小学生的一步大约长50厘米．（）20．是一个仓库侧面墙的示意图．要给这面墙粉刷涂料，粉刷的面积可以用长方形的面积加上梯形的面积．（）21．计算的面积，只能把它分成一个正方形和一个三角形来计算．（）四．计算题22．算出图形的面积。

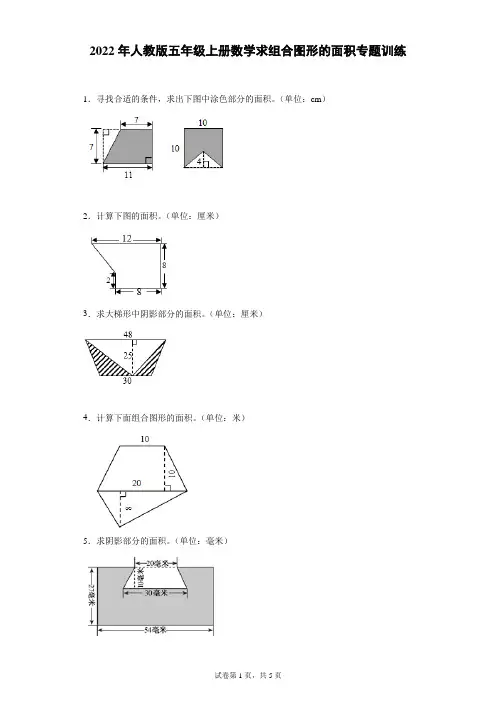
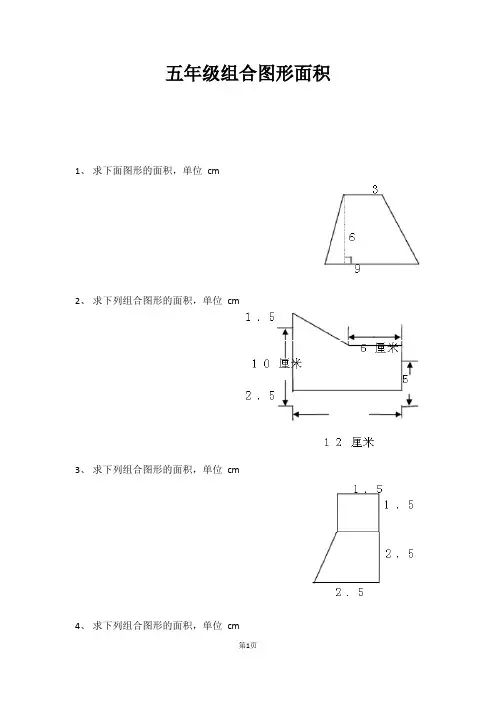
人教版五年级上册数学求组合图形的面积专题训练1．计算下列各图形的面积。

2．求出下面各图形的面积。

（单位：cm）
3．求下图的面积。

（单位：厘米）
5．求出下面图形的面积。

6．下图是两个不同边长的正方形拼成的图形，求出图中阴影部分的面积。

（单位：厘米）7．计算下面图形阴影部分的面积。

（1）（2）
9．求阴影部分的面积。

（单位：cm）
10．计算阴影部分的面积。

（1）（2）11．计算下面图形的面积。

（单位：厘米）
12．求下面各组合图形的面积。

（单位：dm）
（1）
（2）
13．求下列图形中涂色部分的面积。

14．如图，两个正方形的边长分别为6厘米和4厘米，求阴影部分的面积。

15．求涂色部分的面积。

（单位：cm）
（1）
（2）
16．一张长方形纸，向内折起了一个角（如下图），求阴影部分的面积。

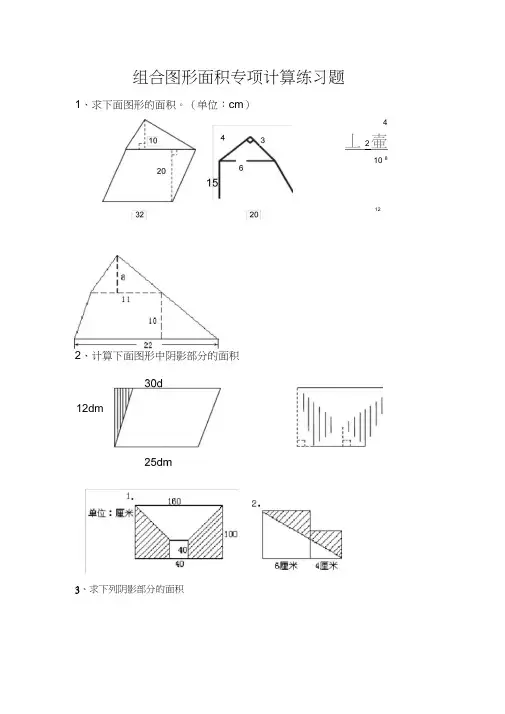
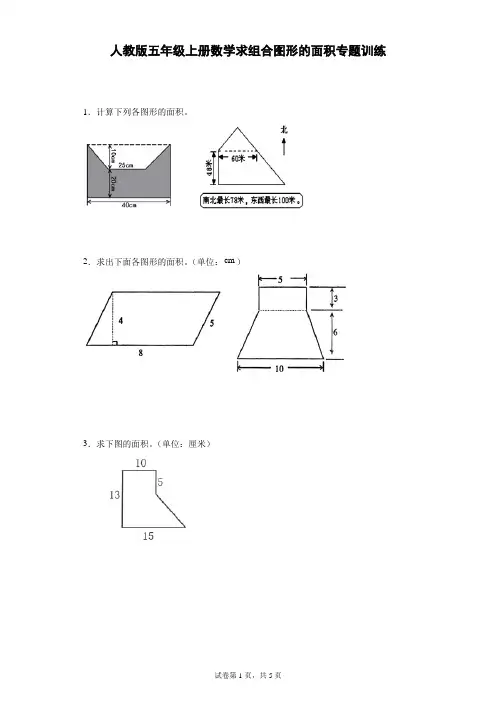
组合图形面积专项计算练习题1、求下面图形的面积。

（单位：cm ）4丄2壷10 82、计算下面图形中阴影部分的面积12dm3、求下列阴影部分的面积1220②已知S 平=48dm 2，求S 阴。

13cm * 16cm卜阳毫戕 ・4、求下面各图形的面积。

（单位：分米）丁D③已知：阴影部分的面积为24平方厘米，求梯形的面积。

④求S 阴。

7 cm12cm4dm5、“实践操作”显身手：1、求下面图形中阴影部分的面积。

14cm16cm6、如右图所示，平行四边形的面积是48平方厘米，求阴影部分的面积。

7、如右图所示，梯形中阴影部分的面积是150平方厘米，求梯形的面积25组合图形是由两个或两个以上的简单的几何图形组合而成的。

组合的形式分为两种：一是拼合组合，二是重叠组合。

由于组合图形具有条件相等的特点，往往使得问题的解决无从下手。

要正确解答组合图形的面积，应该注意以下几点: 1•切实掌握有关简单图形的概念、公式，牢固建立空间观念；2•仔细观察，认真思考，看清所求图形是由哪几个基本图形组合而成的；3•适当采用增加辅助线等方法帮助解题；4•采用割、补、分解、代换等方法，可将复杂问题变得简单。

一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米1 •求四边形ABCD的面积。

（单位：厘米）2 .已知正方形ABCD的边长是7厘米，求正方形EFGH的面积3 •有一个梯形，它的上底是5厘米，下底7厘米。

如果只把上底增加3厘米, 那么面积就增加平方厘米。

求原来梯形的面积。

正图正方形中套着一个长方形，正方形的边长是 12厘米，长方形的四个角的 顶点把正方形的四条边各分成两段， 其中长的一段是短的2倍。

求中间长方形的 面积。

1.（如下图）已知大正方形的边长是 12厘米，求中间最小正方形的面积。

2•正图长方形ABCD 的面积是16平方厘米，E 、F 都是所在边的中点，求三角形 AEF 的面积。

3•求下图长方形ABCD 的面积（单位：厘米）。

【同步专练A】6.4 组合图形的面积(基础应用篇)一、单选题(共8题)1.如图，长方形ABCD的周长是14cm，在它的每条边上各画一个以该边为边长的正方形，已知这四个正方形的面积是50cm2，那么长方形ABCD面积是( )平方厘米．A. 12B. 6C. 10D. 492.一个正方形边长是6真米，如果把它的边长增加2厘米，则它的面积增加( )。

A. 4B. 12C. 283.两个( )的梯形可以拼成一个平行四边形。

A. 形状相同B. 等底等高C. 完全一样D. 大小相等4.在如图梯形中，两个阴影部分的面积相比( )A. 甲大于乙B. 乙大于甲C. 甲等于乙D. 无法比较5.如图A、B分别是长方形长和宽的中点，阴影部分面积是长方形的( )A. B. C. D.6.下图中每个大三角形的大小、形状完全相同，都是正三角形，从第二排选出合适的图形，把这一个图形的序号填在( )里．A. B. C. D.7.下图中阴影甲、阴影乙是梯形中的两个三角形，它俩的面积( )。

A. 相等B. 甲大C. 乙大8.2个边长3厘米的正方形拼成一个长方形，拼成的长方形的周长比原来2个正方形周长和减少了( )厘米。

A. 9B. 6C. 4D. 2二、判断题(共8题)9.任何一个梯形都可以分成两个等高的三角形。

( )10.梯形的上底下底越长，面积越大。

( )11.两个完全一样的梯形可以拼成一个平行四边形。

( )12.用8个1立方厘米的小方块拼成一个正方体．如果拿去一个小方块，它的表面积不变． ( )13.面积相等的图形，形状一定相同．( )14.平行四边形的面积大于梯形面积。

( )15.把一个长方形框架拉成平行四边形，它的面积不变． ( )16.用4个边长1cm的小正方形拼成两个不同的图形，这两个图形的周长不同，面积也不同。

( )三、填空题(共8题)17.下图中每个方格的边长是1厘米，整个图形的周长是________厘米，面积是________平方厘米。

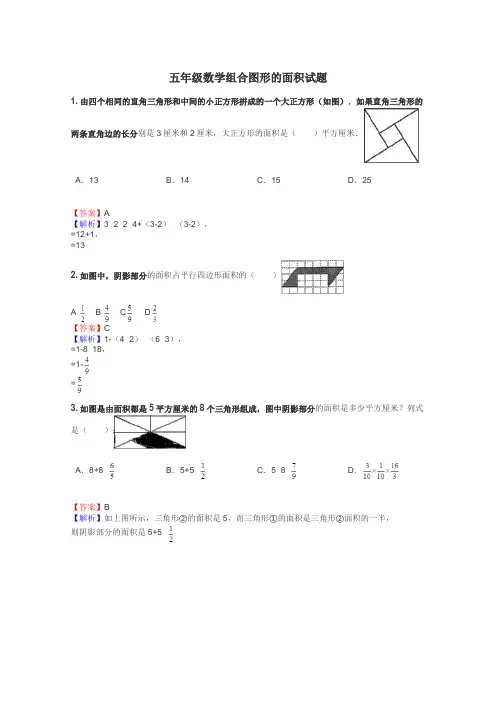
五年级数学组合图形的面积试题1.由四个相同的直角三角形和中间的小正方形拼成的一个大正方形（如图）．如果直角三角形的两条直角边的长分别是3厘米和2厘米，大正方形的面积是（）平方厘米．A．13B．14C．15D．25【答案】A【解析】3×2÷2×4+（3-2）×（3-2），=12+1，=132.如图中，阴影部分的面积占平行四边形面积的（）A B C D【答案】C【解析】1-（4×2）÷（6×3），=1-8÷18，=1-=3.如图是由面积都是5平方厘米的8个三角形组成，图中阴影部分的面积是多少平方厘米？列式是（）A．8+8×B．5+5×C．5×8×D．【答案】B【解析】如上图所示，三角形②的面积是5，而三角形①的面积是三角形②面积的一半，则阴影部分的面积是5+5×4.下列图形的面积是（）A．800B．700C．750D．600【答案】A【解析】观察图形可知，这个图形的面积等于上面的三角形的面积与下面的平行四边形的面积之和，据此利用三角形和平行四边形的面积公式计算即可解答问题。

32×10÷2+32×20=160+640=8005.图中图形的面积最大的是（）A．A B．B C．C【答案】B【解析】设三个图形的高都是h，则：三角形的面积=12h÷2=6h；平行四边形的面积=7h；梯形的面积=（8+3）h÷2=5.5h；7h＞6h＞5.5h，所以平行四边形的面积最大。

6.用同一条铁丝围成下列图形，围成的图形（）的面积最大。

A．圆 B．长方形 C．正方形【答案】A【解析】假设铁丝的长度为12.56分米，则围成的正方形的边长是：12.56÷4=3.14（分米），正方形的面积是：3.14×3.14=9.8596（平方分米）；长方形的长和宽的和是：12.56÷2=6.28（分米），长和宽越接近面积越大，若长可为3.15分米，宽为3.13分米，长方形的面积是：3.15×3.13=9.8595（平方分米）；圆的半径是：12.56÷2÷3.14=2（分米），圆的面积是：3.14×22=12.56（平方分米）；9.8595＜9.8596＜12.56；所以围成的圆的面积最大。

五年级组合图形面积1、求下面图形的面积，单位cm2、求下列组合图形的面积，单位cm3、求下列组合图形的面积，单位cm4、求下列组合图形的面积，单位cm5、求下列组合图形的面积，单位cm6、求阴影图形的面积，单位cm7、求阴影图形的面积，单位cm8、求阴影图形的面积，单位cm9、求阴影图形的面积，单位cm10、求阴影图形的面积，单位cm11、求阴影图形的面积，单位cm12、求组合图形的面积，单位cm13、图中的甲和乙都是正方形，求阴影部分的面积。

（单位：厘米）14、求阴影部分的面积，单位cm15、求阴影部分的面积，单位cm16、图中长方形草地长16米，宽12米，中间有一条宽为2米的道路，求草地（阴影部分的面积）17、长方形的长是8cm，宽是6cm，A和B是宽的中点，求长方形内阴影部分的面积18、求阴影部分的面积。

（单位：cm）19、求下面图形的面积，单位cm20、求下面图形的面积，单位cm21、求下面图形的面积，单位cm22、求下面图形的面积，单位cm23、求下面图形的面积，单位cm24、求阴影部分的面积。

25、求阴影部分的面积。

（单位：cm）26、求阴影部分的面积。

（单位：cm）27、求下面图形的面积。

28、下图是一个饲养场的平面图，一面靠墙，三面用铁丝围起来。

已知铁丝的长度是450米。

求这个饲养场的面积。

29、王大伯利用一面墙围成一个鸡圈（如图），已知所用篱笆全长11.5m，请你帮王大伯，算出这个鸡圈的面积是多少？30、在公路中间有一块三角形草坪（见右图），1平方米草坪的价格是12元，种这块草坪需要多少钱？31、有一个停车场原来的形状是梯形，为扩大停车面积，将它扩建为一个长方形的停车场（如下图），扩后面积增加了多少平方米？32、下图中正方形的周长是32cm，求平行四边形的面积。

33、用总长40米的篱笆，靠墙围成一块梯形（如图）。

已知梯形的高是10米，求菜地的面积？34、下图中，边长为10和15的两个正方形并放在一起，求三角形ABC（阴影部分）的面积，单位cm。

组合图形面积专项计算练习题1、求下面图形的面积.（单位：cm）152、计算下面图形中阴影部分的面积.30d12dm25dm3、求下列阴影部分的面积.201064 34821032 20 12①②已知S平＝48dm2.求S阴.③已知：阴影部分的面积为24 ④求S阴.平方厘米.求梯形的面积.4、求下面各图形的面积.（单位：分米）13cm16cm12cm7cm 8dm8dm3dm5、“实践操作”显身手：6、如右图所示.平行四边形的面积是48平方厘米.求阴影部分的面积.7、如右图所示.梯形中阴影部分的面积是150平方厘米.求梯形的面积16cm12cm14cm 24m10m8m1、求下面图形中阴影部分的面积.2、求下面图形的面积.5625组合图形是由两个或两个以上的简单的几何图形组合而成的.组合的形式分为两种：一是拼合组合.二是重叠组合.由于组合图形具有条件相等的特点.往往使得问题的解决无从下手.要正确解答组合图形的面积.应该注意以下几点：1．切实掌握有关简单图形的概念、公式.牢固建立空间观念；2．仔细观察.认真思考.看清所求图形是由哪几个基本图形组合而成的；3．适当采用增加辅助线等方法帮助解题；4．采用割、补、分解、代换等方法.可将复杂问题变得简单.一个等腰直角三角形.最长的边是12厘米.这个三角形的面积是多少平方厘米？1．求四边形ABCD的面积.（单位：厘米）2．已知正方形ABCD的边长是7厘米.求正方形EFGH的面积.3．有一个梯形.它的上底是5厘米.下底7厘米.如果只把上底增加3厘米.那么面积就增加4.5平方厘米.求原来梯形的面积.正图正方形中套着一个长方形.正方形的边长是12厘米.长方形的四个角的顶点把正方形的四条边各分成两段.其中长的一段是短的2倍.求中间长方形的面积.1．（如下图）已知大正方形的边长是12厘米.求中间最小正方形的面积.2．正图长方形ABCD的面积是16平方厘米.E、F都是所在边的中点.求三角形AEF 的面积.3．求下图长方形ABCD的面积（单位：厘米）.四边形ABCD和四边形DEFG都是正方形.已知三角形AFH的面积是7平方厘米.三角形CDH的面积是多少平方厘米？1．图中两个正方形的边长分别是6厘米和4厘米.求阴影部分的面积.2．下图中两个完全一样的三角形重叠在一起.求阴影部分的面积.（单位：厘米）3．下图中.甲三角形的面积比乙三角形的面积大多少平方厘米？下图中正方形的边长为8厘米.CE为20厘米.梯形BCDF的面积是多少平方厘米？1．如下图.正方形ABCD中.AB=4厘米.EC=10厘米.求阴影部分的面积.2．在一个直角三角形铁皮上剪下一块正方形.并使正方形面积尽可能大.正方形的面积是多少？（单位：厘米）3．图中BC=10厘米.EC=8厘米.且阴影部分面积比三角形EFG的面积大10平方厘米.求平行四边形的面积.图中ABCD是长方形.三角形EFD的面积比三角形ABF的面积大6平方厘米.求ED的长.1．如图.平行四边形BCEF中.BC=8厘米.直角三角形中.AC=10厘米.阴影部分面积比三角形ADH的面积大8平方厘米.求AH长多少厘米？2．图中三个正方形的边长是1厘米、2厘米和3厘米.求图中阴影部分的面积. 3．正方形的边长是2(a+b).已知图中阴影部分B的面积是7平方厘米.求阴影部分A和C的和是多少平方厘米？。

小学五年级数学组合图形的面积试题及答案集团档案编码：[YTTR-YTPT28-YTNTL98-UYTYNN08]五年级数学（上册）：《组合图形的面积》试题1、求图形的面积(单位：厘米)梯形面积：三角形面积：（8+12）×8.5÷212×3÷2=20×8.5÷2=36÷2=170÷2=18（cm2）=85（cm2）图形面积=梯形面积–三角形面积：85-18=67（cm2）2、校园里有两块花圃(如图)，你能计算出它们的面积吗?(单位：m)图形面积=长方形面积6×（5-2）+正方形面积（2×2）图形面积=长方形面积-梯形面积6×（5-2）+2×210×6–[（3+6）×2÷2]=6×3+4=60-[9×2÷2]=18+4=60-9=22（m2）=51（m2）3、下图直角梯形的面积是49平方分米，求阴影部分的面积。

直角梯形的高=直角三角形的高（阴影部分面积）直角梯形的高=49÷（6+8）×2直角三角形面积=6×7÷2=49÷14×2=42÷2=3.5×2=21（dm2）=7（dm2）4、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。

直角梯形的高=直角三角形的高梯形面积=（5+12）×7.5÷2=45÷12×2=17×7.5÷2=3.75×2=127.5÷2=7.5（cm2）=63.75（cm2）阴影部分面积=梯形面积–空白部分面积：63.75-45=18.75（cm2）5、阴影部分面积是40平方米，求空白部分面积。

（单位：米）梯形的高=三角形的高（阴影部分三角形）梯形面积=（6+10）×8÷2=40÷10×2=16×8÷2=4×2=128÷2=8（m2）=64（m2）空白部分面积=梯形面积–阴影部分面积：64–40=24（m2）6、如图，平行四边形面积240平方厘米，求阴影部分面积。

第六单元《多边形的面积》第4课时组合图形的面积一．选择题1．(2012•碑林区校级自主招生)如图,三角形ADF与三角形ABE、四边形AFCE的面积相等,9BC=厘米,6CD=厘米,求阴影部分的面积()A．5(平方厘米)B．25(平方厘米)C．15(平方厘米)D．10(平方厘米)2．(2012•康县)如图中,两三角形的面积之和占长方形面积的()A．12B．13C．14D．163．(2012•常熟市自主招生)如图所示,甲和乙两幅图的面积相等,其阴影面积相比,下列说法正确的是()A．甲>乙B．甲<乙C．甲=乙4．(2019秋•大兴区期末)如图所示,把一个长方形分成一个梯形和一个三角形．已知梯形的面积比三角形的面积大18厘米2,那么梯形的上底长为()厘米．A．2B．3C．4D．65．如图ABCD是长方形,已知4AB=厘米,6BC=厘米,三角形EFD的面积比三角形ABF的面积大6平方厘米,求(ED=)厘米．A．9B．7C．8D．6二．填空题6．(2019春•海淀区月考)如图,有一块长方形场地,长62=,从A、B两处入口的小路宽都AD mAB m=,宽41是1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为2m．7．(2019春•静安区月考)如图的三角形分成两部分,甲的面积是210cm,乙的面积是2cm．8．(2019•徐州)如图中,阴影部分的面积占大长方形的．9．(2019春•湖北月考)如图,梯形的面积是．10．(2019•长沙县)如图,D是BC的三等分点,E是AC的四等分点,三角形ABC的面积是三角形ADE的面积的 倍．11．(2019春•杨浦区月考)如图,已知AE EC =,:2:3BD DC =,AFE ∆的面积比BFD ∆的面积多2,则ABC ∆的面积是12．(1999•广州自主招生)一个宽是3厘米的长方形,如果将长和宽都增加3厘米,那么面积增加81平方厘米；如果将长和宽都减少2厘米,那么面积减少 平方厘米．三．判断题13．如图所示,梯形的上底长等于下底长的一半,空白面积也等于阴影部分面积的一半． (判断对错)四．计算题14．(2018秋•环江县期末)计算下面图中阴影部分的面积．(单位：分米)15．(2019•武侯区)计算下面图形的面积．(单位：)cm16．(2017•西安模拟)求图中阴影部分的面积(单位：厘米) 17．(2015秋•徐州月考)求下列各图形面积18．(2017秋•栖霞区校级期中)求阴影部分面积．19．(2016秋•贵州月考)计算如图各图形的面积．20．计算下面图形中阴影部分的面积．(单位：分米)五．应用题21．(2019春•无棣县期末)在一块长方形地上,种上三种不同的蔬菜,如图．(1)黄瓜地的周长是多少米？(2)西红柿地的面积是多少？22．(2017•武汉模拟)如图,在直角三角形ABC里面裁剪一个正方形CDEF,剩下两个三角形,已知=,则图中阴影部分的面积是多少平方厘米？BE cm=,43AE cm23．(2017秋•巴南区期中)有一块长方形的地如图,中间有两条2m宽的水泥小路,其余部分为草坪,求草坪的面积？24．实验小学评比“卫生文明班级”需要制作一些流动红旗(如图)。

小学五年级数学组合图形的面积试题及答案Prepared on 24 November 2020五年级数学（上册）：《组合图形的面积》试题1、求图形的面积(单位：厘米)梯形面积：三角形面积：（8+12）×÷2 12×3÷2= 20×÷2 = 36÷2= 170÷2 = 18（cm2）= 85（cm2）图形面积= 梯形面积–三角形面积： 85-18=67（cm2）2、校园里有两块花圃(如图)，你能计算出它们的面积吗(单位：m)图形面积=长方形面积6×（5-2）+ 正方形面积（2×2）图形面积=长方形面积 - 梯形面积6×（5-2）+ 2×2 10×6 –[（3+6）×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22（m2） = 51（m2）3、下图直角梯形的面积是49平方分米，求阴影部分的面积。

直角梯形的高=直角三角形的高（阴影部分面积）直角梯形的高= 49÷（6+8）×2 直角三角形面积= 6×7÷2= 49÷14×2 = 42÷2= ×2 = 21（dm2）= 7（dm2）4、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。

直角梯形的高=直角三角形的高梯形面积=（5+12）×÷2= 45÷12×2 = 17×÷2= ×2 = ÷2= （cm2） = （cm2）阴影部分面积=梯形面积–空白部分面积：- 45 = （cm2）5、阴影部分面积是40平方米，求空白部分面积。

（单位：米）梯形的高=三角形的高（阴影部分三角形）梯形面积=（6+10）×8÷2= 40÷10×2 = 16×8÷2= 4×2 = 128÷2= 8（m2） = 64（m2）空白部分面积=梯形面积–阴影部分面积：64–40 = 24（m2）6、如图，平行四边形面积240平方厘米，求阴影部分面积。

1、如图，两个完全相同的直角三角形部分重叠，已知
AB=10厘米，
BD=4厘米，EF=3厘米。

求阴影部分的面积。

2、如图，两个完全相同的直角梯形部分重叠，已知AB=7.5厘米，BC=10厘米，DE=2厘米。

求阴影部分的面积。

3、如图，大小两个正方形的边长都是
10厘米和6厘米，求阴影部分的面积。

A B C
D E
F A
D
E B C
107.52
4、如图，大小两个正方形的边长都是
10厘米和6厘米，求阴影部分
的面积。

5、如图，由长方形ABCD 和直角梯形BEFC 组成，其中阴影部分的面积是36.5平方厘米，CD 是5厘米。

求长方形ABCD 的面积。

6、如图，平行四边形ABCD 的底BC 长12厘米，线段EF 长8.3厘米，求图中阴影部分的面积总和是多少平方厘米？
A
B
C D E F
A
B C D F E G。

五年级数奥数：《组合图形的面积》梯形而积：(8+12) X8.54-2= 20X8.5 十2=1704-2=85 (cm2)图形面积二梯形面积-三角形面积：85-18=67 (cm2)图形面积=长方形曲积6X (5-2) +正方形面积(2X2) 6X(5-2) +2X2=6X3+4=18 + 4=22 (m2)3、下图直角梯形的面积是49平方分米，求阴影部分的而积。

直角梯形的高二直角三角形的高直角梯形的高=49一(6+8) X2= 494-14X2= 3.5X2=7 (dm2)(阴影部分面积)直角三角形面积=6X7F2= 424-2=21 (dm2) 4、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。

直角梯形的高二直角三角形的高= 45-M2X2= 3.75X2= 7.5 (cm2)梯形面积二(5+12) X7.54-2=17X7.5 一2=127.54-2=63.75 (cm2)阴影部分面积二梯形面积-空白部分面积：63.75 - 45 = 18.75 (cm2)122、校园里有两块花圃(如图), 你能计算出它们的面积吗?(单位：m)101、求图形的面积(单位：厘米)三角形而积:12X34-2= 364-2=18 (cm2)图形面枳二长方形面积-梯形面枳10X6 - [ (3+6) X24-2]=60-[ 9X2H-2]= 60-9=51 (m2)梯形面积二(6+10) X84-2=16X84-2 =1284-2 =64 (m 2)6、如图，平行四边形面积24()平方厘米，求阴影部分面积。

梯形的下底二平行四边形的底= 2404-12=20 (cm)梯形面积二(15+20) XI24-2= 35X12 — 2 = 4204-2 = 210 (cm 2)阴影部分面积二平行四边形面积-梯形面积：240-210 = 30 (cm 2)7、下图ABCD 是梯形，它的面积是140平方厘米，已知AB=15厘米，DC=5厘米。

人教版数学五年级上册6.4 组合图形的面积练习卷一、选择题1．如图，阴影部分的面积是16dm2，平行四边形的面积是（）dm2．A．48B．32C．642．下图为一幅图形的密铺方案，则此影阴部分的面积与空白部分的面积比为（）A．2∶1B．7∶9C．1∶1D．3∶43．如图，长方形ABCD中，AB=12厘米，BC=8厘米，平行四边形BCEF的一边BF 交CD于G，若梯形CEFG的面积为64平方厘米，则DG长为（）A．3B．4C．5D．64．图中每个小方格的面积为1cm2，脚印的面积大约是（）。

A．5cm2——50cm2B．10cm2——28cm2C．28cm2——50cm2 5．如下图，每个方格的面积为1平方厘米。

请你估一估，这个图案的面积约为（）。

A．20平方厘米B．11平方厘米C．9平方厘米D．7平方厘米6．估计一下，下图不规则土地的面积约是（）。

A．216m 36m B．224m C．2二、图形计算7．[多种思路求面积]．你能计算出图中这个多边形的面积吗？8．计算下面图形的面积。

（单位：厘米）三、填空题9．如图，两个正方形的边长分别是6厘米、4厘米，阴影部分的面积是_____平方厘米。

10．如图，A是平行四边形BC边上的中点，阴影部分面积是2平方厘米，则平行四边形的面积是平方厘米．11．下图中，长方形长10厘米，宽6厘米，E为AB边上任一点，三角形EDC（即阴影部分）的面积是________平方厘米．12．如图，5个相同的小长方形拼成一个周长是88厘米的大长方形，那么大长方形的面积是_____平方厘米。

13．下图中每个小方格的面积表示21cm，估算一下，阴影部分的面积大约是( )2cm。

14．如图中三个正方形的边长分别为10，20，30，那么图中阴影部分的面积是．15．如图，大小两个正方形拼在一起，阴影部分面积为28平方厘米，小正方形边长为4厘米，则图中空白部分的面积是平方厘米．16．如图，四边形ABCD是一个梯形，由三个直角三角形拼成；它的面积是_____cm2。

组合图形的面积1.组合图形的面积（1）下面组合图形的面积是______平方厘米。

（2）下面组合图形是由一个正方形和有一个平行四边形组成，它的面积是______平方厘米。

（3）下面组合图形的面积是______平方厘米。

（4）下面组合图形的面积是______平方厘米。

（5）下图阴影部分的面积是______平方厘米。

（单位：厘米）（6）下图阴影部分的面积是______平方分米。

（单位：分米）2.替换法求三角形或梯形的面积（1）三角形ABC与三角形DFE是两个完全相同的直角三角形，把它们的一部分叠放在一起，如下图所示，阴影部分的面积是_____平方厘米。

(单位：cm)（2）如右图，三角形ABC与三角形DFE是两个完全相同的直角三角形，把它们的一部分叠放在一起，如下图所示，阴影部分的面积是_____平方厘米。

(单位：cm)（3）三角形ABC与三角形EFD是两个完全相同的直角三角形，把它们的一部分叠放在一起，如下图所示，阴影部分的面积是______平方厘米。

(单位：cm)（4）如下图所示，两个完全相同的梯形重叠放在一起，阴影部分的面积是______平方厘米。

(单位：cm)（5）如下图所示，两个完全相同的梯形重叠放在一起，阴影部分的面积是______平方厘米。

(单位：cm)（6）如右图所示，两个完全相同的梯形重叠放在一起，阴影部分的面积是______平方厘米。

(单位：cm)3.面积差不变-线段围成的图形（1）已知长方形的长为6厘米，宽为2.5厘米，三角形的底边长为6厘米，高为2厘米，这两个图形有一小部分重合了，则它们没有重合的部分的面积相差______平方厘米（2）边长为5厘米和4厘米的两个正方形有一小部分重合，则它们没有重合的部分的面积相差______平方厘米（3）已知梯形的上底长4厘米,下底长为7厘米,高为3厘米,这个梯形与一个边长为3厘米的正方形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米（4）已知三角形ABC的底边BC长为4厘米,高为3厘米,三角形DEF的底边EF 长为5厘米,高为6厘米,这两个三角形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米（5）已知平行四边形的底边长为7厘米,高为3厘米,三角形的底边长为6厘米,高为5厘米,这两个图形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米（6）图中甲的面积比乙的面积大4平方厘米,三角形ABC的底边长为4厘米,高为2.5厘米,那么三角形DEF的面积是______平方厘米（7）图中甲的面积比乙的面积小5平方厘米，正方形ABCD的边长为5厘米，那么三角形ABF的面积是______平方厘米4.有关直角梯形的面积（1）如图所示，直角梯形ABCD的高AB长26厘米，AD长24厘米，△DEF的面积是175.5平方厘米，EF的长度是BC的二分之一，梯形ABCD的面积是______平方厘米。

五年级数奥数：《组合图形的面积》1、求图形的面积(单位：厘米)梯形面积：三角形面积：（8+12）×÷2 12×3÷2= 20×÷2 = 36÷2= 170÷2 = 18（cm2）= 85（cm2）图形面积= 梯形面积–三角形面积： 85-18=67（cm2）2、校园里有两块花圃(如图)，你能计算出它们的面积吗(单位：m)图形面积=长方形面积6×（5-2）+ 正方形面积（2×2）图形面积=长方形面积 - 梯形面积6×（5-2）+ 2×2 10×6 –[（3+6）×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22（m2） = 51（m2）3、下图直角梯形的面积是49平方分米，求阴影部分的面积。

直角梯形的高=直角三角形的高（阴影部分面积）直角梯形的高= 49÷（6+8）×2 直角三角形面积= 6×7÷2= 49÷14×2 = 42÷2= ×2 = 21（dm²）= 7（dm²）4、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。

直角梯形的高=直角三角形的高梯形面积=（5+12）×÷2= 45÷12×2 = 17×÷2= ×2 = ÷2= （cm2） = （cm2）阴影部分面积=梯形面积–空白部分面积： - 45 = （cm2）5、阴影部分面积是40平方米，求空白部分面积。

（单位：米）梯形的高=三角形的高（阴影部分三角形）梯形面积=（6+10）×8÷2= 40÷10×2 = 16×8÷2= 4×2 = 128÷2= 8（m2） = 64（m2）空白部分面积=梯形面积–阴影部分面积：64–40 = 24（m2）6、如图，平行四边形面积240平方厘米，求阴影部分面积。