三年级奥数教程第12讲三阶幻方

三年级三阶幻方教案教学目标：1.认识幻方的概念与特点2.观察规律，独立思考，培养创新能力3.提高孩子们的数字观念、计算能力和逻辑思维能力教学重点：1.认识幻方的概念，并熟练掌握三阶幻方的构造方法2.在构造幻方的过程中培养孩子们的逻辑思维和创新能力教学难点：1.帮助学生理解并掌握幻方的构造方法，以及规律的产生2.培养学生探究和解决问题的能力教学方法：1.探究式授课，教师启发学生思考，并引导学生自主探索2.幻方题材的小游戏，引发学生的兴趣教学步骤：一、导入（5分钟）学生们围坐在一起，老师让他们自由讨论一下：在生活中，有没有什么东西是由数字组成的？学生举手回答：电影票，电话号码，截止时间等等。

然后老师介绍一下数字的重要性，并向学生们简单介绍一下幻方。

二、学习三阶幻方构造方法（20分钟）1、什么是幻方？介绍幻方的概念。

2、幻方的规律是什么？如何构造三阶幻方？具体方法如下：首先，把1放在第一行的正中间，即第一行第二列的位置上。

然后，从2开始依次向右上方移动。

例如:2放在第一行第三列，3放在第一行第四列，4放在第二行第四列，5放在第三行第四列，依此类推。

当填满最后一个数字9时，构成了一个三阶幻方。

3、举例说明构造幻方的方法。

三、动手实践掌握方法（15分钟）让学生们在黑板上模仿示范，用纸与笔模拟三阶幻方的构造过程。

引导学生们分别画出三阶幻方的所有行、列、对角线的和，帮助他们了解幻方规律。

四、小游戏巩固知识（15分钟）让学生组成小组，在班级大屏幕上进行幻方小游戏，比赛哪个小组先完成一道三阶幻方。

对于初学幻方的学生，老师可以将部分三阶幻方数字进行提前给出，让学生根据此构造幻方。

五、总结（5分钟）通过学习与实践，学生们对幻方有了更广泛的了解，老师总结本堂课的内容，帮助学生回顾今天所学的知识点，鼓励他们在后续学习中勇敢尝试。

六、作业布置（5分钟）1、让学生自己动手构造一个三阶幻方。

2、让学生在家里找一些数字物品，写下他们的数字，并尝试构造幻方。

三阶幻方最简单的口诀1. 幻方的魅力你有没有听说过三阶幻方？这东西可有意思了，简单来说，就是一个3×3的方阵，里面填上1到9的数字，要求每一行、每一列和两个对角线的数字加起来都得是同一个数。

听起来是不是有点复杂？别着急，咱们慢慢聊。

首先，咱们得知道，这个“同一个数”其实是15。

因为1+2+3+4+5+6+7+8+9加起来是45，而这个45再分成三组，每组15。

想想看，真的挺神奇的吧！这就像是数学里的魔法，既简单又有趣。

说到这，谁还没被这样的魔法吸引呢？2. 如何排列2.1 排列步骤要想轻松搞定三阶幻方，我们得有个简单的口诀。

听好了，首先，把数字1放在中间上方的格子里。

然后，接下来放的数字要遵循一个“左上右下”的原则。

具体点说，就是当你放了一个数字之后，接下来的数字应该在它的右上方，如果那个位置已经有数字了，那就往下移动一格，继续放。

2.2 举个例子比如说，第一步你放上1，然后接下来的数字2，你就要放在1的右上方，结果发现位置空着，就放上去。

接着放3，你会发现3的右上方位置又空着，继续放。

如果不小心越过了边界，别担心，直接从对面的边界进来就行。

记住，永远都不能让数字重叠。

这样排下去，慢慢的，你会发现所有的数字都能填满，最后的结果可真是让人眼前一亮。

虽然看起来好像有点绕，但其实只要试几次，你就能熟能生巧，像老手一样轻松掌握。

3. 幻方的乐趣3.1 朋友聚会的小把戏你可以想象一下，在朋友聚会的时候，突然用这个三阶幻方给大家来一段小表演，肯定能吸引眼球。

大家围过来，啊呀，怎么做到的呀！你就可以得意洋洋地跟他们说：“这可是我最近学会的绝活！”多么拉风啊，简直就像是从魔术师的手中变出来的一样。

3.2 学习中的好帮手而且，这三阶幻方还不仅仅是个游戏。

它还可以锻炼我们的逻辑思维，特别适合那些喜欢挑战自己的朋友们。

就像古人说的“开卷有益”，我们在玩乐中学习，顺便培养我们的耐心和专注力，真是一举两得。

在这个快节奏的生活中，抽出一点时间，和家人朋友一起围坐，动动脑筋，不仅能拉近彼此的距离，也能享受那种解谜后的成就感。

三阶幻方原理及填法嗨，朋友们！今天咱们来聊聊一个超级有趣的数学小玩意儿——三阶幻方。

这三阶幻方啊，就像是数学世界里的一个神秘小魔法阵，可有意思啦。

我先给你们说说啥是三阶幻方。

简单来讲，就是用1到9这九个数字，填在一个3×3的方格里面，使得每行、每列还有两条对角线上的数字之和都相等。

这个相等的和呢，就叫幻和。

你想啊，这九个数字就像九个调皮的小娃娃，要把它们安排在这九个格子里，还得让每行每列和对角线上的数字之和都一样，是不是感觉像在玩一个超级有挑战性的数字拼图游戏呢？那这个幻和是多少呢？这可不难算哦。

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45，因为三阶幻方有三行（或者三列），所以幻和就是45÷3 = 15。

这就像是我们找到了这个魔法阵的一个关键密码一样。

我有个朋友，之前第一次接触三阶幻方的时候，就皱着眉头跟我说：“这怎么填啊？感觉无从下手呢！”我就跟他说：“嘿，别急，这里面可有不少小窍门呢。

”有一种比较简单的填法。

咱们先把1放在这个3×3方格的最中间那一行最左边的那个格子里。

这就像是先在魔法阵里种下一颗数字的种子。

然后呢，按照斜着往上走的规则来填数字。

如果斜着往上走的时候，走出了这个方格，那就像这个数字小娃娃调皮地跑到方格外面去了，怎么办呢？这时候就把它拉回来，拉到这个方格相对应的另一边的位置上。

比如说，如果斜着往上走，数字跑到方格的左上角外面去了，那就把它放到右下角的格子里。

当我们按照这个方法填到数字3的时候，就会发现如果再斜着往上走，那个格子已经有数字1了。

这就像两个小娃娃抢一个小格子，那可不行。

这时候呢，我们就把数字3填在数字2的下面。

就像数字3说：“既然上面的地方被占了，那我就乖乖在2下面呆着吧。

”按照这个规则一直填下去，就能把这个三阶幻方填出来啦。

哇，当你把最后一个数字填好的时候，那种成就感就像是你自己创造了一个小奇迹一样。

不过呢，还有其他的填法哦。

三年级三阶幻方教案1. 简介幻方是一种古老而有趣的数学谜题，被广泛用于培养学生的逻辑思维和数学推理能力。

本教案主要介绍如何在三年级教学中引入三阶幻方，帮助学生学习和理解该数学概念，并通过实践操作提高他们的解决问题能力和团队合作能力。

2. 教学目标•了解幻方的概念和特点•能够构造出三阶幻方•提高学生的逻辑推理和解决问题能力•培养学生的团队合作和沟通能力3. 教学准备•幻方的定义和特点•三阶幻方的构造方法•三阶幻方的实例•学生黑板和白板笔•学生练习册和作业本•计时器•分组命名牌4. 教学过程步骤1：引入幻方概念（15分钟）•向学生简单介绍幻方的定义和特点，强调幻方中每行、每列和对角线上的数之和都相等。

•展示一些幻方实例，并让学生观察规律和特点。

步骤2：构造三阶幻方（30分钟）•向学生讲解构造三阶幻方的方法：1.将数字1放在第一行的中间位置；2.从数字2开始，按照右上方45度方向填充数字，如果方格已被填充则向下一行移动；3.如果移动到最右上角，则转移到最左下角继续填充。

•按照上述方法，现场演示如何构造出一个三阶幻方。

•让学生分组练习构造三阶幻方，并设定时间限制。

步骤3：讨论和总结（15分钟）•让每个小组展示他们构造的三阶幻方，并让其他小组检查其正确性。

•引导学生讨论构造幻方时的策略和规律，总结构造三阶幻方的步骤和技巧。

步骤4：解决问题和拓展（30分钟）•提出一些有关幻方的问题，让学生在小组内讨论和解决，例如找出对角线上所有数字之和等于某个特定值的幻方。

•鼓励学生分享解决问题的方法和思路。

•将解决问题的时间限制在一定范围内，促进学生合作和集体智慧。

步骤5：作业和反思（10分钟）•发放练习册和作业本，让学生完成相关练习题。

•邀请学生分享他们在本节课中的学习感悟和困惑。

5. 教学拓展•引导学生尝试构造其他阶数的幻方，如四阶、五阶等，并探究其构造方法和规律。

•引导学生寻找幻方与数学中其他概念的联系，如平方数、素数等。

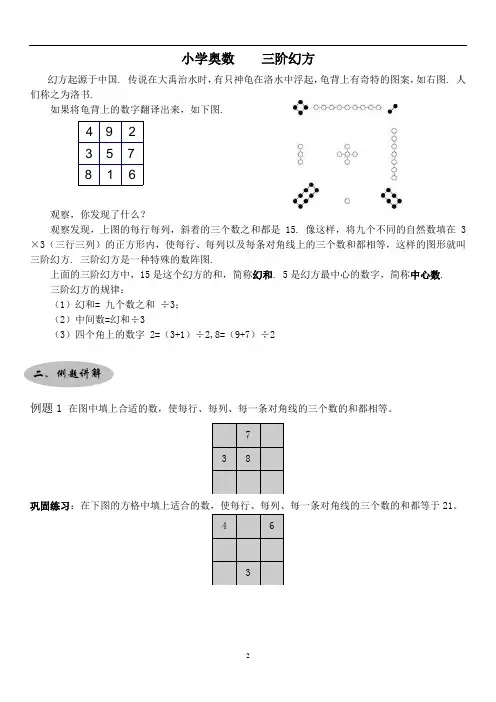
小学奥数 三阶幻方幻方起源于中国. 传说在大禹治水时，有只神龟在洛水中浮起，龟背上有奇特的图案，如右图. 人们称之为洛书.如果将龟背上的数字翻译出来，如下图.观察，你发现了什么？观察发现，上图的每行每列，斜着的三个数之和都是15. 像这样，将九个不同的自然数填在3×3（三行三列）的正方形内，使每行、每列以及每条对角线上的三个数和都相等，这样的图形就叫三阶幻方. 三阶幻方是一种特殊的数阵图.上面的三阶幻方中，15是这个幻方的和，简称幻和. 5是幻方最中心的数字，简称中心数. 三阶幻方的规律：（1）幻和= 九个数之和 ÷3； （2）中间数=幻和÷3（3）四个角上的数字 2=（3+1）÷2,8=（9+7）÷2例题1 在图中填上合适的数，使每行、每列、每一条对角线的三个数的和都相等。

巩固练习：在下图的方格中填上适合的数，使每行、每列、每一条对角线的三个数的和都等于21。

73 84 63 二、例题讲解 672159834例题2在下图中填上适当的数，使每行、每列、每条对角线上的三个数的和都相等。

巩固练习：根据三阶幻方的特点，完成下列幻方。

例题3 在下图的每个空格中填入小于12且互不相同的九个自然数，使得每行、每列及每条对角线上的三个数之和都等于21。

巩固练习：在下列右图空着的方格内填上合适的数，使得每一横行、每一竖列和对角 线上的三个数之和都等于27。

例题4 将1～9这九个自然数填在下面图中的九个方格里，使每行、每列、两条对角线上的三个数的和都相等。

19 1410 18 812介绍杨辉法：介绍公式法：口诀：九子斜列，上下对易，左右相更，四维挺出。

想一想还有没有其他填法：第一种：816 357 492第二种：618 753 294第三种：492357816第四种：294753618第五种：672159834第六种：834159672第七种：276951438第八种：438951276巩固练习：用3-11构造一个三阶幻方课堂练习1、把4～12九个数填入方格中，使每行、每列、每一条对角线的三个数的和都相等。

三阶幻方的解法最简单的口诀三阶幻方是指一个 $3\\times 3$ 的矩阵，其中填入了 $1$ 至 $9$ 的数字，使得每个数字在该矩阵中出现且仅出现一次，并且每行、每列和两条对角线的数字和均相等。

解决三阶幻方问题最简单的口诀如下：1. 定义首先，我们需要明确一些基本的概念和定义。

矩阵：$m \\times n$ 的矩阵是一个由 $m$ 行、$n$ 列数字（称为元素）所组成的矩形数组，通常用方括号表示，如下所示：$$\\begin{bmatrix}a_{11} & a_{12} & \\cdots & a_{1n} \\\\a_{21} & a_{22} & \\cdots & a_{2n} \\\\\\vdots & \\vdots & \\ddots & \\vdots \\\\a_{m1} & a_{m2} & \\cdots & a_{mn}\\end{bmatrix}$$矩阵元素：矩阵中每一个数字称为矩阵元素。

对角线：矩阵中从左上角到右下角和从右上角到左下角的线称为对角线。

主对角线：从左上角到右下角的对角线称为主对角线。

副对角线：从右上角到左下角的对角线称为副对角线。

2. 解法接下来，我们将逐步介绍如何解决三阶幻方问题。

步骤 1：确定中间的数字由于每行、每列和两条对角线的数字和均相等，因此中间的数字必须是$5$。

$$\\begin{bmatrix}\\emptyset & \\emptyset & \\emptyset \\\\\\emptyset & 5 & \\emptyset \\\\\\emptyset & \\emptyset & \\emptyset\\end{bmatrix}$$步骤 2：填充四个角的数字要求每行、每列和两条对角线的数字和均相等，因此填充四个角的数字时需要保持对称。

三阶幻方同学们：在33⨯（三行三列）的正方形方格中，既不重复又不遗漏地填上1—9这9个连续的自然数，使每行、每列、每条对角线上的三个自然数的和均相等，这样的图形叫做三阶幻方。

如果在44⨯（四行四列）的正方形方格中进行填数，就要不重复，不遗漏地在44⨯方格内填上16个连续自然数，且使每行、每列、每条对角线的四个自然数之和均相等，这样的图形叫四阶幻方。

一般地，在几×几（几行几列）的方格里，既不重复又不遗漏地填上几×几个连续自然数，（注意这几×几个连续自然数不一定非要从1开始），每个数占一个格，且每行、每列、每条对角线上的几个自然数和均相等，我们把这个相等的和叫做幻和，几叫做阶，这样排成的数的图形叫做几阶幻方。

（一）思路指导与解答例1. 用1～9这九个数编排一个三阶幻方。

a bc def g hi图1 图2分析：我们先用a 、b 、c 、d 、e 、f 、g 、h 、i 分别填入九个空格内以代表应填的数。

看图（2）：（1）通过审题，我们知道幻和是多少才好进行填数。

同时可以看到图（2）中，e 是一个中间数，也是关键数。

因为它分别要与第二行、第二列以及两条对角线上的另外两个数进行求和运算，结果都等于幻和；其次是三阶幻方中四个角上的数：a 、c 、g 、i 它们各自都要参加一行，一列及一条对角线的求和运算。

如果e 以及四个角上的数被确定之后，其它的数字便可以根据幻和是多少填写出来了。

（2）求幻和：幻和=++++++++÷()1234567893=÷=45315（3）选择突破口，显然是e ，看图2。

因为：a e i b e h c e g d e f ++=++=++=++=15 所以：()()()()a e i b e h c e g d e f +++++++++++ =+++=1515151560也就是：()a b c d e f g h i e +++++++++⨯=360 又因为：a b c d e f g h i ++++++++=45 所以45360+⨯=e 36045⨯=-ee =5也就是说，图1中的中心方格中应填5，请注意，这个数正好是1～9这九个数中正中间的数。

三阶幻方知识点总结
以下是一份关于“三阶幻方知识点总结”的文稿：
前言
嘿，朋友！你可知道三阶幻方有多神奇吗？就好像一个神秘的魔法盒子，里面藏着好多奇妙的秘密等待我们去发现呢！今天就让我们一起揭开三阶幻方的神秘面纱吧！
正文
三阶幻方，简单来说，就是把 9 个数字填到一个3×3 的格子里，让每行、每列和对角线上的数字之和都相等。

就像搭积木一样，得把这些数字巧妙地组合起来。

比如说，1、2、3、4、5、6、7、8、9 这九个数字，你得
把它们摆得恰到好处才行呢！
那怎么才能摆好呢？这就得讲究技巧啦！中心位置很关键呀，就好比是球队的核心球员一样重要。

一般中心位置填的数字得好好斟酌。

而且，幻方中相对的两个数字之和通常也是相等的哦，你说神奇不神奇！比如，左上角和右下角的数字拿出来一加，嘿，和右上角和左下角的数字之和一样呢！
想想看，这就像是一个精巧的拼图游戏，每个数字都有它自己的位置，找对了位置，整个图案就完整了。

我们来举个例子感受一下吧。

喏，看这个三阶幻方，每行每列和对角线的和都是 15 呀，是不是超级酷？
结尾
哎呀呀，三阶幻方是不是特别有趣啊！它就像一个充满惊喜的小宝藏，越挖越有料！大家快去试试，看看自己能不能也创造出神奇的三阶幻方吧！。

三阶幻方的解题方法嘿，朋友们！今天咱来聊聊三阶幻方的解题方法，这可有意思啦！三阶幻方呢，就像是一个神秘的小魔法阵。

你看啊，它就像是一个九宫格，要把一些数字巧妙地放进去，让每行、每列以及对角线上的数字之和都相等。

这可不是随便乱放就能行的哦！咱先来说说怎么开始。

就好像你要搭积木，得先找到那个最关键的基石。

在三阶幻方里，中间那个格子就特别重要。

一般来说，先把中间的数字确定好，就像是给这个魔法阵找到了中心一样。

然后呢，你可以试着从一些比较特殊的数字入手。

比如说，最小的数字或者最大的数字，把它们放在合适的位置。

这就好比你挑衣服，先选一件最喜欢的，其他的再慢慢搭配嘛。

接着呀，你得不断地尝试和调整。

这可不是一蹴而就的事儿，就跟你走路一样，可能会走几步弯路，但最后总能找到正确的方向。

有时候你觉得这个数字放这儿挺好，可再一看，哎呀，不行，得换个地方。

别着急，慢慢来，就像解开一个小谜题。

你想想看，这三阶幻方不就像是一个小小的智力挑战游戏吗？每次尝试都是一次冒险，每次调整都是一次探索。

当你终于找到了那个完美的组合，哇，那种成就感，简直比吃了蜜还甜！比如说，你看这个三阶幻方，一开始可能乱七八糟的，数字们就像调皮的小孩子到处乱跑。

但你耐心地哄着它们，让它们一个个找到自己的位置，最后整整齐齐的，多棒呀！而且哦，解三阶幻方还能锻炼你的大脑呢！让你的思维变得更敏捷，就像给大脑做了一次健身操。

这多好呀，既能玩得开心，又能变得更聪明。

所以啊，大家别害怕三阶幻方，大胆地去尝试吧！别觉得它很难，只要你用心，肯定能搞定它。

就像爬山一样，虽然过程有点累，但当你站在山顶俯瞰风景的时候，一切都值得啦！三阶幻方就是这样一个有趣又有挑战的东西，等着你们去征服它呢！。

三阶幻方公式简易口诀三阶幻方是指由1到9的九个数字组成的一个3x3的方阵，使得方阵中的每一行、每一列以及对角线上的数字之和都相等。

下面是一个简单的口诀来求解三阶幻方的公式：首先，我们需要把9个数字按照一定的规律填入到3x3的方阵中。

设置一个3x3的方阵如下：abcdefghi第一步：选取任意一个数字填入中间的位置，比如选取数字5，填入方阵的中心位置e：abcd5fghi第二步：根据魔方的特性，可以得出以下规律：1.真正的幻方中心位置的值将会是(n^2+1)/2，对于三阶幻方来说，中心位置的值为(3^2+1)/2=52.方阵的每个角的位置必须是n的倍数，对于三阶幻方来说，四个角的值即为1、3、7、9根据以上两个规律，我们可以进行以下步骤填充幻方：第三步：将数字1填入到方阵的上一个位置g（此处的上指的是在方阵中“上方”相对于中心位置e的方向）：abc15fghi第四步：根据规律2，将数字9填入到方阵的下一个位置f（此处的下指的是在方阵中“下方”相对于中心位置e的方向）：abc159ghi第五步：根据规律2，将数字3填入到方阵的下一个位置h（此处的下指的是在方阵中“下方”相对于中心位置e的方向）：abc159g3i第六步：根据规律2，将数字7填入到方阵的下一个位置d（此处的下指的是在方阵中“下方”相对于中心位置e的方向）：abc15973i第七步：根据规律1，将数字8填入到方阵的下一个位置b（此处的下指的是在方阵中“下方”相对于中心位置e的方向）：a8c15973i第八步：根据规律1，将数字4填入到方阵的下一个位置f（此处的下指的是在方阵中“下方”相对于中心位置e的方向）：a8c159734最终得到了一个三阶幻方。

利用以上口诀和规律，我们可以通过简单的步骤来构造三阶幻方。

通过这个口诀，我们可以快速而准确地创建出一个三阶幻方，仅需一些简单的数字填充操作。

三年级三阶幻方教案一、教学目标通过本节课的学习，学生将能够:1.理解什么是幻方及其基本概念；2.掌握构建三阶幻方的方法；3.进行三阶幻方的验证和解答。

二、教学准备1.幻方定义及基本概念的PPT；2.三阶幻方构建方法的示意图；3.操作练习的练习册；4.学生桌上分发的幻方纸板。

三、教学步骤步骤一：引入幻方的定义和基本概念（10分钟）1.准备一张PPT，向学生展示幻方的定义和基本概念。

解释幻方是指由n行、n列的方阵组成的数表，其中每行、每列和对角线上的元素之和都相等。

2.与学生互动讨论，让他们理解幻方的概念并举例说明。

步骤二：讲解三阶幻方构建方法（15分钟）1.在PPT上使用示意图演示三阶幻方构建的方法。

解释每个步骤的含义和操作方法。

2.强调每行、每列和对角线上的和都应该相等，提示学生观察规律和自己思考。

步骤三：操作实践练习（20分钟）1.给每个学生发放一张幻方纸板，并让他们按照步骤二的方法构建一个三阶幻方。

2.学生按照步骤操作，并在纸板上填写数字，确保每行、每列和对角线上的和相等。

3.鼓励学生互相合作，相互交流和讨论，并提供必要的帮助。

步骤四：验证和解答（15分钟）1.让学生逐个展示他们构建的幻方，然后让其他学生验证其是否正确。

2.对于错误的幻方，指导学生找出错误并进行修改。

3.带领学生一起解答构建三阶幻方的过程，总结规律。

步骤五：课堂总结（10分钟）1.回顾本节课的学习内容，让学生总结三阶幻方构建的方法和规律。

2.强调幻方思维的重要性，培养学生的观察力和逻辑思维能力。

四、课后练习1.布置学生完成练习册上相关练习题，巩固幻方的构建方法和规律；2.提醒学生完成课后作业，写一篇关于幻方的文章，介绍幻方的定义、构建方法以及一些有趣的幻方例子。

五、教学反思本节课通过引入幻方的定义和基本概念，讲解三阶幻方的构建方法，以及操作实践练习和验证解答，使学生掌握了构建三阶幻方的方法和规律。

通过课堂互动和讨论，加深了学生对幻方概念的理解和思维能力的培养。

三阶幻方概念及求法三阶幻方啊，这可是个挺有趣的东西呢。

就像是一个小小的数字魔法阵。

啥是三阶幻方呢？简单来说，就是一个三行三列的正方形格子，每个格子里都得填个数字，这些数字从1开始，一直到9，不多不少正好九个数字。

而且填进去之后啊，这个方阵就有神奇的性质了。

你看啊，不管是横着加，每一行数字加起来的和都相等；竖着加呢，每一列数字加起来的和也和那行的和一样；就连从左上角到右下角的对角线，还有从右上角到左下角的对角线，这两条对角线上数字加起来的和，都跟行和列的和是相同的。

这就好像是一群小伙伴，不管怎么组队，他们的力量总和都是一样的，是不是很神奇呢？那这三阶幻方的数字该怎么填呢？这就像是在解一个有趣的谜题。

有一种比较简单的方法。

咱们先把1放到这个方阵的最下面一行中间的格子里。

这就像在游戏里先找个起点一样。

然后呢，咱们要按照一定的规则把剩下的数字放进去。

下一个数字要放在这个数字的右上方的格子里。

但是呢，如果这个右上方的格子跑到方阵外面去了，那就得像玩贪吃蛇一样，从方阵的另一边钻进来。

比如说，要是1的右上方跑到方阵外面了，那就得把下一个数字放到这个方阵最上面一行的最右边的格子里。

还有啊，如果这个右上方的格子已经被别的数字占了，那就得把下一个数字放到这个数字的正下方的格子里。

咱们按照这个规则来填数字。

1放好了，它的右上方应该放2，可是跑到方阵外面了，那2就放到最上面一行最右边的格子。

2的右上方是3，那就把3放到2的右上方的格子里。

3的右上方是个已经有数字的格子，那4就只能放到3的正下方。

接着按照这个规则一直填下去，直到把9也放进去。

这样啊，一个三阶幻方就完成了。

你可能会想，这有啥用呢？嘿，这可不仅仅是个数字游戏呢。

这就好比是数学里的一颗小宝石，它能锻炼咱们的思维能力。

你想啊，就像搭积木一样，每个数字都得放到合适的位置，这得动不少脑筋呢。

而且啊，三阶幻方在数学的历史长河里也有不少故事呢。

在古代，很多数学家都对它感兴趣。

三年级三阶幻方教案一、引言幻方是一种特殊的正方形矩阵，其中每一行、每一列和对角线的元素之和相等。

在数学教育中，通过幻方的学习和探索，可以培养学生的逻辑思维、数学运算能力、空间认知能力等。

本文档将介绍三年级学生学习三阶幻方的教学方法和相关练习。

二、教学目标1.了解幻方的定义和特点；2.能够构造和解答三阶幻方；3.培养学生的逻辑思维和数学运算能力。

三、教学内容1.幻方的概念和特点–定义：幻方是一个由数字组成的正方形矩阵，其中每一行、每一列和对角线的元素之和相等。

–特点：幻方中的数字范围从1到n²，n为幻方的阶数，每个数字只能使用一次。

2.三阶幻方的构造方法–基本构造法：从1开始，依次填入幻方的每个位置。

| 2 | 7 | 6 ||---|---|---|| 9 | 5 | 1 || 4 | 3 | 8 |–数学公式法：根据规律填入幻方的每个位置。

| 8 | 1 | 6 ||---|---|---|| 3 | 5 | 7 || 4 | 9 | 2 |3.三阶幻方的解答方法–列消元法：根据幻方的特点，将三阶幻方的第一列转化为123（n²的每个数字只能使用一次）。

–辅助数法：根据幻方的特点，通过填入辅助数字来解答幻方。

例如，将幻方的第一行填入1,2,3，然后推导出其他位置的数字。

四、教学步骤1.引入幻方的概念和特点，让学生了解幻方的定义和规律。

2.展示三阶幻方的不同构造方法，引导学生思考幻方的构造规律。

3.分组活动：让学生用基本构造法和数学公式法进行幻方的构造，并分享自己的思路和结果。

4.学生自主解答三阶幻方的解答方法，通过列消元法和辅助数法进行解答。

5.分组对练：学生进行三阶幻方的解答比赛，以提高学生的逻辑思维和解题速度。

6.结束活动：复习幻方的构造和解答方法，并对学生的表现进行评价和总结。

五、教学评价方法1.老师观察学生的课堂表现，包括学生对幻方概念的理解、构造方法的掌握和解答能力的运用。

三年级三阶幻方教案
一、教学目标：
1.能够掌握幻方的基本概念、构成要素。

2.能够使用幻方笔记本，求解各种三阶幻方问题。

3.掌握基本的求解步骤，根据求解思路解决幻方问题
二、学习内容：
1.幻方的基本概念和构成要素
2.使用幻方笔记本，求解各种三阶幻方问题
3.掌握基本的求解步骤，根据求解思路解决幻方问题
三、教学过程：
第一步：了解学生对幻方的基本概念和构成要素
（1）教师让学生集体说出他们对幻方的理解，引出讨论，让学生掌握幻方的概念。

（2）朗读幻方的基本介绍，让学生了解幻方的基本构成要素。

第二步：使用幻方笔记本，求解各种三阶幻方问题
（1）准备幻方求解模板和笔记本，教师演示一个三阶幻方的求解过程。

（2）让学生分组使用模板和笔记本，练习求解几个三阶幻方
第三步：掌握基本的求解步骤，根据求解思路解决幻方问题
（1）让学生分组讨论，提出求解三阶幻方的基本步骤。

（2）准备各种三阶幻方，让学生根据求解思路，运用刚才掌握的步骤求解。

四、课后作业：
1.自选一个三阶幻方，尝试着用笔记本求解。

2.选择几道三阶幻方，用书面文字描述求解的步骤。

3.尝试画出三种以上不同的三阶幻方。

三年级奥林匹克数学专题讲解——三阶幻方理论A 篇幻方实际上是一种填数游戏，它不仅有三阶，还有四阶、五阶……直到任意阶。

一般地，在n 行n 列的方格里，既不重复也不遗漏地填上n n ⨯个连续的自然数，每个数占一格，并使排在每一行、每一列以及每条对角线上n 个自然数的和相等，我们把这几个相等的和叫做幻和，n 叫做阶，这样排成的图形叫做n 阶幻方。

三阶幻方：在三行三列的正方形方格中，既不重复也不遗漏地填上33⨯个连续的自然数，每个数占一格，并使排在每一行、每一列以及每条对角线上3个自然数的和均相等。

通常这样的图形叫做三阶幻方。

三阶幻方的一些基本规律：幻和=九个数之和÷3，中间数=幻和÷3。

九个连续的自然数中，第五个数是中间数，第二、四、六、八个数是四个角上的数。

例题1 在下面的方格中填上适当的数，使每行、每列和每条对角线上的三个数的和都等于24。

分析： 解决问题的突破口：找出每行、每列和每条对角线上的任意两个数，就可以根据幻和求出第三个数。

例题2 下图中，每个字母代表一个数。

已知每行、每列、每条对角线上的三个数和都相等，若4,16,17,5a l d h ====。

求b 与f 为多少？分析： 根据幻和相等：a e l c e g b e h d e f ++=++=++=++，这4个算式中都有中间数e ，所以有：a l c g b h df +=+=+=+。

再代入4,16,17,5a l d h ====即可。

一、知识介绍二、例题讲解例题3 编出一个三阶幻方，使其幻和为27。

分析： 先根据幻和求中间数，然后填其他数。

请你试一试：调换数的位置，还可以得到几种答案？例题4 将1～9这九个自然数填在下面图中的九个方格里，使每行、每列、两条对角线上的三个数的和都相等。

分析： 先求幻和，再根据幻和求中间数，然后填其他数。

例题5 下图中，a g 7个字母，各代表7个数字，要使三阶幻方成立，“a ”所代表的数字是多少？分析： 根据幻方的概念：每一行、每一列以及每条对角线上3个自然数的和均相等。

三阶幻方同学们：在（三行三列）的正方形方格中，既不重复又不遗漏地填上1—9这9个连续的自然数，使每行、每列、每条对角线上的三个自然数的和均相等，这样的图形叫做三阶幻方。

如果在（四行四列）的正方形方格中进行填数，就要不重复，不遗漏地在方格内填上16个连续自然数，且使每行、每列、每条对角线的四个自然数之和均相等，这样的图形叫四阶幻方。

一般地，在几×几（几行几列）的方格里，既不重复又不遗漏地填上几×几个连续自然数，（注意这几×几个连续自然数不一定非要从1开始），每个数占一个格，且每行、每列、每条对角线上的几个自然数和均相等，我们把这个相等的和叫做幻和，几叫做阶，这样排成的数的图形叫做几阶幻方。

（一）思路指导与解答例1. 用1～9这九个数编排一个三阶幻方。

分析：我们先用a、b、c、d、e、f、g、h、i分别填入九个空格内以代表应填的数。

看图（2）：（1）通过审题，我们知道幻和是多少才好进行填数。

同时可以看到图（2）中，e是一个中间数，也是关键数。

因为它分别要与第二行、第二列以及两条对角线上的另外两个数进行求和运算，结果都等于幻和；其次是三阶幻方中四个角上的数：a、c、g、i它们各自都要参加一行，一列及一条对角线的求和运算。

如果e以及四个角上的数被确定之后，其它的数字便可以根据幻和是多少填写出来了。

（2）求幻和：幻和（3）选择突破口，显然是e，看图2。

因为：所以：也就是：又因为：所以也就是说，图1中的中心方格中应填5，请注意，这个数正好是1～9这九个数中正中间的数。

（4）四个角上的数，a、c、g、i的特点。

我们先从a开始：想：a是奇数还是偶数。

如果a为奇数，因为，所以也是奇数。

因为奇＋奇＝偶。

又因为，所以d与g同是奇数或同是偶数。

分两种情况：<1>当d、g都是奇数时，因为，，其中e，i都是奇数，所以f、h也只能是奇数。

这样在图1中应填的数有a、d、e、f、g、h、i这七个奇数，而1～9中九个数只有五个奇数，所以矛盾，说明d、g不可能为奇数。