幻方与数阵试题

幻方与数阵图1.在幻方中．每行、每列和每条对角线上的数的和都相同，那么在下图所示的未完成的幻方中该是____。

2.幻方是将n2个数（不重复）排列成纵、横各有n个数的方阵，使其每行、每列和两条对角线上n个数相加的和都相等．请问下图3×3的幻方中丁是多少？3.在下图所示的O内填入不同的数，使得三条边上的三个数的和都是12．若A、B、C的和为18，则三个顶点上的三个数的和是________。

4.下图3×3正方形的每个方格内的字母都代表一个数，已知其每行，每列以及两条对角线上三个数之和都相等，若“a=4，d=19，l=22，那么6=_______，h=______。

5.在图1、图2的空格中分别填人适当的数，使得横、竖及对角线上的三个数之和都相等，那么“？”处的数字分别为多少？．6．在下图中每个小方格中填人一个数，使每一行每一列都有1、2、3、4、5，那么，右上角小方格内填人的数字，应该是________。

7.下图是一个3×3幻方，满足每行、每列及两条对角线上三数之和都相等，那么其中“★代表的数是__________。

8.下边的一排方格中，除9、8外，每个方格中的汉字都表示一个数（不同的汉字可表示相同的数），已知其中任意3个连续方格巾的数加起来都为22，则“走”+“进”+“数”+“学”+“花”+“园”=__________。

9.所谓“三阶乘法幻方”是指在3×3的方格中填入9个不等于0的整数，使得每行、每列及每条对角线上的三个数之积都相等，请将下图的“乘法幻方”补充完整，则其中的“”所代表的数是___________。

10.将1至8这八个自然数分别填入下图中的正方体的八个顶点处的o内，并使每个面上的四个O内的数字之和都相等，求与填人数字1的O有线段相连的三个O内的数的和的最大值．11.将从8开始的11个连续自然数填入下图中的圆圈内，要使每边上的三个数之和都相等，中间数共有__________种填法．12.将1--12这十二个自然数分别填人下图的12个圆圈内，使得每条直线上的四个数之和都相等，这个相等的和为___________。

尤新教育奥数标准教程第八讲简单的数阵与幻方【知识点与方法】一、数阵和幻方的概念：（1）数阵：每一条直线段的数字和相等。

（2）幻方：在一个由若干个排列整齐的数组成的正方形中，任意一横行、一纵行及对角线的和都相等。

二、联系之前所学的高斯求和的知识，首先找到中心项：首项、末项、中间项。

然后对称找和相等的成对的项。

【经典例题】例1、将1、2、3、4、5这五个数分别填入下图中，使横行3个数的和与竖行3个数的和相等。

例2、将1、4、7、10、13这五个数分别填入下图中，使横行3个数的和与竖行3个数的和都等于25。

例3、将1～7这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都相等。

例4、将5～11这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都等于24。

例5、将1～9这九个自然数填入下图的九个方格内，使得它成为一个幻方（每行、每列、每条对角线和都相等）。

练习与思考1.将3、6、9、12、15这五个数分别填入下图中，使横行3个数的和与竖行3个数的和相等。

2. 将1、3、5、7、9这五个数分别填入下图中，使横行3个数的和与竖行3个数的和为17。

（2题图）（3题图a）（3题图b）3. 将1～9这九个数分别填入右上图的小方格里，使横行和竖列上五个数之和相等。

(至少找出两种本质上不同的填法)4.将3～9这七个数分别填入左下图的○里，使每条直线上的三个数之和等于20。

（4题图）（5题图）5.将1～11这十一个数分别填入右上图的○里，使每条直线上的三个数之和相等，并且尽可能大。

6. 将2～10这九个自然数填入下图的九个方格内，使得它成为一个幻方（每行、每列、每条对角线和都相等）。

7.将1～7这七个数分别填入下图的○里，使得每条直线上三个数之和与每个圆圈上的三个数之和都相等。

蔚然教育精品班导学案例题1从小华家到学校有3条路可走，从学校到文峰公园有4条路可走。

从小华家到文峰公园，有几种不同的走法？例题2 用红、绿、黄三种信号灯组成一种信号，可以组成多少种不同的信号？思路导航：要使信号不同，要求每一种信号颜色的顺序不同，我们可以把这些信号进行列举：例题3一个长方形的周长是22米，如果它的长和宽都是整米数，那么这个长方形的面积有多少种可能？思路导航：由于长方形的周长是22米，可知它的长与宽之和为11米。

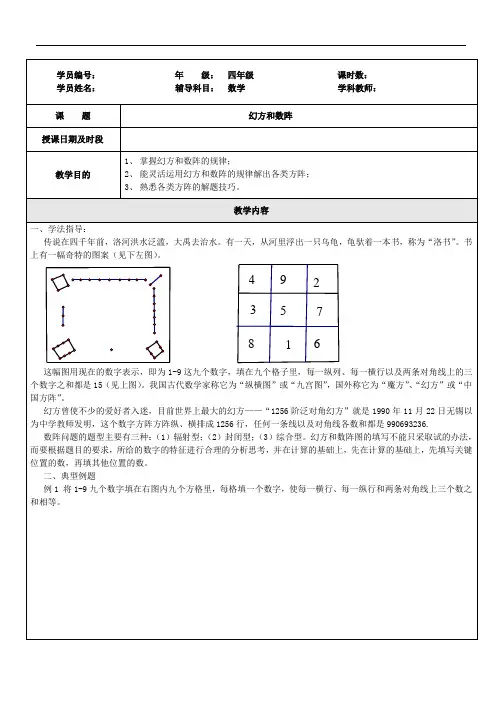
第6讲幻方和数阵图传说在五千年前，大禹治水的时代，人们在黄河中发现一只大龟，龟背上有一些奇怪的图案，经过破译，人们将龟背上的神奇的图案译成了如下图这样的数阵图，也称做幻方。

幻方和数阵是我国文化遗产之一，早在公元前4世纪就有“河图”、“洛书”的传说与记载。

到了宋朝，杨辉对幻方已有较详细的记述，并探索出一些编制方法。

明朝程大位、清朝张潮等人，创制了绚丽多彩的幻方与数阵图式，其中九宫图是最简单的三阶幻方。

将三阶幻方推广，结合某些几何图形，把一些数字填入图形的某种位置上，并使数字满足一定的约束条件，这类问题，通常被称为“数阵图”。

幻方是特殊的数阵图。

大约在15世纪初，幻方传到国外，引起了欧洲很多数学家的兴趣，发现许多新成果。

人们发现幻方不仅仅是一种数字游戏，而且与实验方案的设计及一些高深数学分支有关，幻方已成为数阵图中最重要的课题，是数学研究中的一个重要分支。

数阵图大致分三种：封闭型数阵图、开放型数阵图和复合型数阵图。

幻方的特点：一个幻方每行、每列、每条对角线上的几个数的和都相等。

这个相等的和叫“幻和”。

要求在n行n列的方格里，既不重复又不遗漏地填上n×n个连续的自然数。

这些自然数所组成的一列数有极强的规律性，按顺序排列后，每一项都比它前面的一项大1，即知识梳理它们构成了差相等的数列，是等差数列。

因此在解答这类问题时，常用的知识有：1．等差数列的求和公式总和=（首项+末项）×项数÷22．数字的奇偶性奇数±奇数=偶数偶数±偶数=偶数奇数±偶数=奇数可简记为：同性为偶，异性为奇（注：同性是同奇或同偶，异性是指一奇一偶）。

数阵图【例1】★如图所示，在三个圆圈中各填入一个自然数，使每条线段两端的两个数之和均为奇数。

请问这样的填法存在吗?如不存在，请说明理由；如存在，请写出一种填法。

【解析】不存在，设所填的数分别是a，b，c，如图所示。

假设 a+b=奇数． a+c=奇数，b+c=奇数，左边=2(a+b+c)，是偶数，右边=三个奇数相加，是奇数，偶效≠奇数。

拓展、把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于8和10。

例2、将1—7七个自然数分别填入图中的圆圈里，使每条线上三个数的和相等。

拓展、将1～7这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都等于10。

例3、把1～5这五个数填入下图中的○里(已填入5)，使两条直线上的三个数之和相等。

拓展、将 10～20填入下图的○内，其中15已填好，使得每条边上的三个数字之和都相等。

例4、将1—10这十个数填入下图小圆中，使每个大圆上六个数的和是30。

拓展、将1~8个数分别填入图中,使每个圆圈上五个数和分别为20,22。

例5、把1—10这十个数分别填入下图的○内，使每个四边形顶点的○内四个数的和都相等，且和最大。

拓展、将1～11这十一个数分别填入下图的○里，使每条直线上的三个数之和相等，并且尽可能大。

例6、将1—6六个数分别填入下图的○内，使每边上的三个○内数的和相等。

拓展、将1—8八个数分别填入下图的○内，使每条边上三个数的和相等。

例7、将1—8这八个数分别填入下图○内，使外圆四个数的和，内圆四个数的和以及横行、竖行上四个数的和都等于18。

拓展、将1—8八个数填入下图方格里，使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。

例8、将1—9九个数分别填入下图○内，使外三角形边上○内数之和等于里面三角形边上○内数之和。

拓展、将1—9填入下图的○中，使横、竖行五个数相加的和都等于25。

例9、如下图，将1～9这九个数字填在方格里，使每行、每列、每条对角线上的三个数之和都相等。

拓展、将1—9九个自然数分别填入下图的九个小三角形中，使靠近大三角形每条边上五个数的和相等，并且尽可能大。

这五个数之和最大是多少？例10、将4～12这九个数字填在下图所示的3×3的方格中，使每行、每列及两条对角线上的三个数的和都相等。

拓展、下图的每个空格中，填入不大于12且互不相同的九个自然数，使每行、每列、每条对角线上的三个数之和都等于21。

三年级奥数幻方与数阵训练题
奥林匹克数学竞赛或数学奥林匹克竞赛，简称奥数。

奥数考试想要拿高分，练习题训练是少不了的，因为练习题可以巩固知识，下面是小编整理的相关练习，希望对你有帮助!
1、根据表中数字排列规律，在空格中填上适当的数。

12345
23456
3456
2、根据图中直行数字的排列规律，在○内填上适合的数。

3、自然数按下面规律排列，第8行的第2个数是什么?28应该是第几行左起的第几个数。

12345
109876
1112131415
2019181716
4、在下面数阵中，第8行的第8个数是多少?
1
23
456
78910
1112131415
…………………
5、观察下面各题中数的变化规律，然后填上各题中所缺的数。

5306
4287
38
8715
146
9318
6、下面哪一项数字可以代替表格中的问号? 6257
83177
92177
7410?
A24
B30
C18
D12
E26。

幻方与数阵图扩展第4讲——复杂数阵图情课堂激例1：请将1至10填入图中的10个圆圈中(9已经填好)，使得除了第一行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差。

9练习1：请将1至6填入图中的6个圆圈中(3已经填好)，使得除了第一行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差。

3例2：将1~9全部填入图中，除了正方形四个角上填入同一个数字，其余8个圆圈填入互不相同的数字，使得每条直线上的4个数之和以及大圆上的4个数之和都相等，那么这个和是________。

例3：将数字1,2,3,4,5,6,7填入图中的小圆圈内，使得每个圆周上的3个数之和与每条直线上的3个数之和都相等。

练习2：将1,3,5,9,11,13这6个数填入图中的6个小圆内，使得每条直线上的两数之和相等，两个大圆上3个数的和也相等。

例4：将1至9填入图中的9个圆圈内，使4个大圆周上的4个数之和都等于16。

练习3：将1至12填入图中的12个区域内，其中一部分已经填好，使得每个圆圈内的4个数之和都相等。

例5：图中一共有10个方格，现在把2至11这10个自然数填到里面每个方格各填一个。

如果要求图中的3个2×2的正方形中的4个数之和都相等，那么这个和最小可能是______，请给出一种填法。

6 107 128 9练习4：图中一共有7个区域，现在把1至7这7个自然数都填到里面，每个方格各填一个。

如果要求图中的3个大三角形中的3个数之和都相等，那么这个和最小是______，请给出一种填法。

例6：如图，大三角形被分成了9个小三角形。

试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内，每个小三角形内填一个数，要求靠近大三角形三条边的每5个数相加的和相等。

这5个数的和最大可能是_______，请给出一种填法。

练习5：如图，大三角形被分成了9个小三角形。

试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内，要求每4个小三角形组成的新三角形内(如图中阴影部分为其中一个)的4个数之和相等。