超磁致伸缩滚珠丝杠副智能预紧技术 著作
- 格式:docx
- 大小:37.66 KB
- 文档页数:4


科技信息1.超磁致伸缩材料的特点与应用1.1超磁致伸缩材料的特点磁致伸缩材料主要有三大类:磁致伸缩的金属与合金、铁氧体磁致伸缩材料和稀土金属间化合物磁致伸缩材料。
前两种称为传统磁致伸缩材料,其磁致伸缩应变过小,没有推广应用价值。
而稀土金属间化合物磁致伸缩材料也称为稀土超磁致伸缩材料。
与其他智能材料相比,稀土超磁致伸缩材料具有以下特点:应力负载大(可达700MPa)、能量转换率高(机电耦合系数可达0.75)、温度适应范围宽(小于200℃)、响应快(微秒级)、驱动电压低(小于30V)等。
另外具有频率特性好,工作频带宽;稳定性好,无疲劳,无过热失效等优点。
因此有专家认为,稀土超磁致伸缩材料可广泛应用到机械、电子、航天、农业等其他领域,是21世纪的战略材料。
1.2超磁致伸缩材料的应用分析迄今已有1000多种超磁致伸缩材料器件问世,应用面涉及航空航天、国防军工、电子、机械、石油、纺织、农业等诸多领域,大大促进了相关产业的技术进步。
超磁致伸缩材料在声频和超声技术方面也有广阔的应用前景,国外已用超磁致伸缩材料来制造出超大功率的超声波换能器。
日本已用稀土超磁致伸缩材料来制造海洋声学断层分析系统和海洋气候声学温度测量系统的水声发射换能器,可用于测量海水温度和海流的分布图。
德国材料研究所已将超磁致伸缩薄膜材料应用于微型泵的研究之中。
随科技发展的日新月异,超磁致伸缩材料的重要性必将越来越突出,应用也将更广泛。
预计未来超磁致伸缩材料的应用领域包括航空航天、超精密机械加工、海洋工程、汽车制造、石油产业等。
1.3超磁致伸缩材料在我国的研究与应用在国内,北京钢铁研究总院于1991年率先制备出GMM棒材,此后又开展了低频水声换能器、光纤电流检测、大功率超声焊接换能器等的研究。
北京科技大学采用具有自主知识产权的一步法工艺和设备生产稀土超磁致伸缩材料,减少了过程污染,杂质和氧含量低,合金成分控制准确,提高了材料的性能和产品的一致性;同时易于实现自动化控制,生产效率比传统工艺提高了100-150倍,成本大大降低。
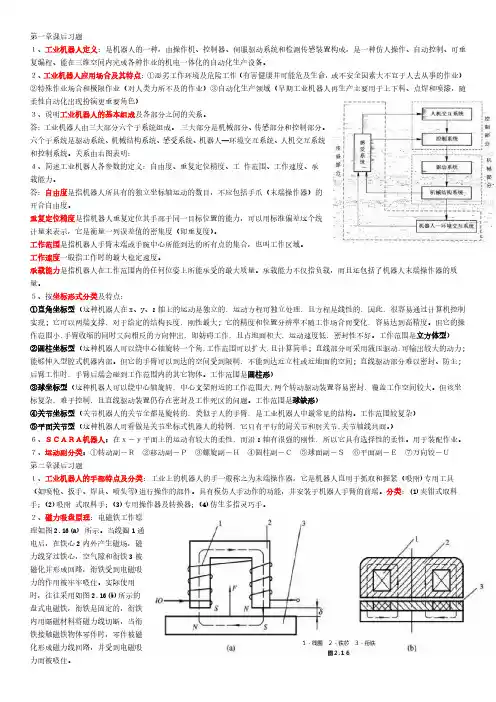
第一章课后习题1、工业机器人定义:是机器人的一种,由操作机、控制器、伺服驱动系统和检测传感装置构成,是一种仿人操作、自动控制、可重复编程、能在三维空间内完成各种作业的机电一体化的自动化生产设备。
2、工业机器人应用场合及其特点:①恶劣工作环境及危险工作(有害健康并可能危及生命,或不安全因素大不宜于人去从事的作业)②特殊作业场合和极限作业(对人类力所不及的作业)③自动化生产领域(早期工业机器人再生产主要用于上下料、点焊和喷漆,随柔性自动化出现扮演更重要角色)3、说明工业机器人的基本组成及各部分之间的关系。
答:工业机器人由三大部分六个子系统组成。
三大部分是机械部分、传感部分和控制部分。
六个子系统是驱动系统、机械结构系统、感受系统、机器人—环境交互系统、人机交互系统和控制系统。
关系由右图表明:4、简述工业机器人各参数的定义:自由度、重复定位精度、工 作范围、工作速度、承载能力。
答:自由度是指机器人所具有的独立坐标轴运动的数目,不应包括手爪(末端操作器)的开合自由度。
重复定位精度是指机器人重复定位其手部于同一目标位置的能力,可以用标准偏差这个统计量来表示,它是衡量一列误差值的密集度(即重复度)。
工作范围是指机器人手臂末端或手腕中心所能到达的所有点的集合,也叫工作区域。
工作速度一般指工作时的最大稳定速度。
承载能力是指机器人在工作范围内的任何位姿上所能承受的最大质量。
承载能力不仅指负载,而且还包括了机器人末端操作器的质量。
5、按坐标形式分类及特点:①直角坐标型(这种机器人在x、y、z轴上的运动是独立的, 运动方程可独立处理, 且方程是线性的, 因此, 很容易通过计算机控制实现; 它可以两端支撑, 对于给定的结构长度, 刚性最大; 它的精度和位置分辨率不随工作场合而变化, 容易达到高精度。
但它的操作范围小,手臂收缩的同时又向相反的方向伸出, 即妨碍工作, 且占地面积大, 运动速度低, 密封性不好。
工作范围是立方体型)②圆柱坐标型(这种机器人可以绕中心轴旋转一个角,工作范围可以扩大,且计算简单; 直线部分可采用液压驱动,可输出较大的动力; 能够伸入型腔式机器内部。


永磁同步电机的书籍永磁同步电机是一种具有高效率、高功率密度和低噪音的电机,目前正被广泛应用于电动汽车、风力发电、工业机器人等领域。
想要深入了解永磁同步电机的原理、结构和应用,可以参考以下几本书籍。
1.《永磁同步电机设计与控制》作者:姚剑平本书介绍了永磁同步电机的设计方法和控制策略,包括永磁电机的基本原理、磁场分析、参数计算、热特性分析等。
另外,本书还详细讨论了永磁同步电机的控制技术,包括IPMSM开环控制、矢量控制等,并提供了控制算法的代码实现。
2.《永磁同步电机设计制造技术与应用》作者:宋桂木,潘树伟,徐银平该书以永磁同步电机的设计、制造和应用为主线,介绍了永磁材料、电磁分析和磁场调制等技术的应用,系统地分析了永磁同步电机的磁路、电路和控制系统,并以汽车驱动电机、机器人电机等实际应用为例进行了说明和分析。
3.《永磁电机及其控制技术》作者:王亮,赵天杰本书系统地介绍了永磁同步电机的原理和控制技术,包括永磁电机的动态特性、电磁场分析、参数计算、磁场调制和控制策略等。
此外,本书还讨论了永磁电机在电动汽车、风力发电、轨道交通等领域的应用实例,并对永磁同步电机未来的发展趋势进行了展望。
4.《永磁同步电机控制技术与应用》作者:王亮,任忠贤本书全面介绍了永磁同步电机的控制技术和应用实例,包括控制器的设计和控制方法的选择等。
此外,本书还系统地阐述了永磁同步电机在电动汽车驱动、工业机器人等领域的应用,并对未来永磁同步电机的市场前景进行了分析和展望。
综上所述,永磁同步电机是一种功能强大的电机,其应用领域广泛。
这些书籍可以帮助读者全面认识永磁同步电机的原理和控制技术,有助于深入了解和应用永磁同步电机。

磁滞伸缩驱动器磁滞特性的Persiach模型建模冒鹏飞;王传礼;喻曹丰;钟长鸣【摘要】Giant magnetostrictive material (GMM) exists intrinsic magnetic hysteresis nonlinearity, large hysterisis error will happened when it is used for precision positioning, accurate mathematical model to describe the hysteresis nonlinearity seems very important in control the output accuracy of the giant magnetostrictive actuatort.%超磁致伸缩材料具有本征磁滞非线性,用于精密定位时具有较大的回程误差.为控制超磁致伸缩驱动器的输出位移精度,需要建立准确的数学模型来描述其磁滞非线性.基于经典的Preisach磁滞模型,通过对Preisach磁滞模型的离散化,建立了超磁致伸缩驱动器的Preisach磁滞数学模型;并进行了超磁致伸缩驱动器输出位移实验研究.实验结果表明:模型计算的结果和实验结果基本吻合,证明所建模型能够较好地反映实际情况.【期刊名称】《科学技术与工程》【年(卷),期】2017(017)009【总页数】4页(P149-152)【关键词】超磁致伸缩材料(GMM);磁滞非线性;Preisach磁滞模型;离散化【作者】冒鹏飞;王传礼;喻曹丰;钟长鸣【作者单位】安徽理工大学机械工程学院,淮南 232001;安徽理工大学机械工程学院,淮南 232001;安徽理工大学机械工程学院,淮南 232001;安徽理工大学机械工程学院,淮南 232001【正文语种】中文【中图分类】TB34超磁致伸缩材料(gaint magnetostrictive material,GMM)是铁磁性功能材料[1],具有磁致伸缩应变大、能量密度高、响应速度快、输出力大、磁机耦合系数大、居里温度高等优点[2],并且能够实现电磁能—机械能的可逆转化,被称作是21世纪战略性高科技材料[2,3]。

专利名称:PHASE INTERPOLATOR发明人:SHI, Ming申请号:EP19219260.7申请日:20191223公开号:EP3675359A3公开日:20200708专利内容由知识产权出版社提供专利附图:摘要:The invention relates to the technical field of high-speed data transmission, and more particularly, to a phase interpolator. The phase interpolator comprises a phase adjusting circuit, and the phase adjusting circuit comprises a first phase adjusting module and a second phase adjusting module, the first phase adjusting module outputs a firstclock signal, and the second phase adjusting module outputs a second clock signal; the first phase adjustment module and the second phase adjustment module are connected in parallel to output an interpolation signal. The technical scheme provided by the invention has the beneficial effects that through the first phase adjustment module and the second phase adjustment module the first clock signal and the second clock signal with the same frequency and different phases are mixed in proportion by adopting a voltage mode to generate an interpolation signal with the same frequency and the phase between the first clock signal and the second clock signal so as to achieve the purpose of phase adjustment, and meanwhile, the circuit can be carried out under lower voltage, so that the power consumption of the phase adjusting circuit is further reduced.申请人:Amlogic (Shanghai) Co., Ltd.地址:Room 207 No. 518 Bibo Road China (Shanghai) Pilot Free Trade Zone Pudong Shanghai 201203 CN国籍:CN代理机构:Kondrat, Mariusz更多信息请下载全文后查看。


![【精品】《机电一体化系统》春数控技术(机电)专科[1]..](https://uimg.taocdn.com/955a0620c8d376eeafaa3148.webp)
《机电一体化系统》春数控技术(机电)专科[1]..教育部人才培养模式改革和开放教育项目湖州广播电视大学《机电一体化系统》形成性考核作业学生姓名学号班级湖州广播电视大学编制一、填空题第一章1. 机电一体化是和相互融合的产物,是机械的、、和上引进微电子技术,并将机械装置与电子装置与相关软件有机结合而构成系统的总称。
2. 机电一体化正朝着、、、和系统化方向发展。
3. 机电一体化系统主要由5个子系统构成、、、和。
4. 常用的机电一体化设计方法有、和。
第二章5. 机械系统一般由、、、和组成。
6. 机械系统的功能是。
在整个机械系统中,控制、和组成的子系统完成单一的机械运动,若干个子系统通过计算机协调完成完整的机械运动。
7. 机械传动要完成机械运动,、、要相互影响、相互作用。
8. 按传递力的方法分类,机械传动装置可分为装置和装置。
9. 常见的传动装置有和装置。
10. 滚珠丝杆副传动装置由、、以及滚珠循环装置。
11. 滚珠丝杆副可将变为直线运动,又可将直线运动变为。
12. 滚珠丝杆副中滚珠的循环方式有和两种。
13. 滚珠丝杆副的螺纹滚道截面型式有和两种。
14. 滚珠丝杠副的轴向间隙是工作时与接触点的弹性变形引起的螺母位移量。
15. 齿轮传动装置是、和的变换器。
16.齿轮传动消除间隙的方法有和两种。
17.在双螺母垫片式调隙法中,调整使两个螺母产生,从而消除几何间隙和轴向间隙。
18. 滚珠丝杆的支撑常采用以为主的轴承组合。
19.求体积小、重量轻的齿轮传动系统常采用的原则。
20. 以提高传动精度和减小回程误差为主的降速传动齿轮系采用原则。
21. 导轨副是导向装置的常见件,由和两部分组成。
22. 滚动直线导轨的运动方向为,支承导件与运动件的两接触面见为,中间介质为滚动体。
二、简答题第一章1.简述机电一体化技术的特征。
2.简述机电一体化技术的重要性。
3.简述与机电一体化系统相关的技术。
4.简述机电一体化系统的设计原则。
5.简述机电一体化系统的设计步骤。

先进制造技术复习题一、填空题1.先进制造技术包含、和三个技术群。
2.制造系统是由制造过程及其所涉及、和组成的一个有机整体。
4.根据产品的信息来源,反求工程可分为,和。
5.先进制造工艺技术的特点除了保证优质、高效、低耗外,还应包括和。
6.微细加工中的三束加工是指,,。
8. 柔性制造系统的组成包括:,,和一套计算机控制系统。
12. CIMS的三要素分别为、、。
20.快速原型制造技术的熔丝沉积成形法通常采用的原材料是。
21.精密与超精密加工有色金属时,常用的刀具材料为。
22.FMS的机床配置形式通常有,和。
23.超精密机床导轨的主要形式有:,和25.与传统制造技术比较,先进制造技术具有的特征是:,,和。
26.从时间维的角度划分,产品设计的四个阶段分别为:,,,。
27.优化设计的三要素是:,,。
28.反求工程的主要影响因素包括:,,。
32.超硬磨料砂轮通常采用的结合剂形式包括:,,。
33.高速主轴采用的轴承有:滚动轴承,,,。
34.高速切削机床的工作台的快速进给多采用和来实现。
35. MRPⅡ可分为、和三大子系统。
37.工业机器人一般由,,和等几个部分组成。
38. MRP和MRPII分别是指和,而ERP是指,其核心思想是。
43.高速切削通常使用的刀具材料有:1)硬质合金涂层刀具23)4)44.工业机器人的按系统功能分:1)2)3)4)45.工业机器人的性能特征:、、、、。
48.MRPⅡ是一个集、、和财务为一体的信息管理系统.49.微量进给装置有机械或液压传动式,、、、、压电陶瓷式等多种结构形式。
50.一个典型的FMS刀具运储系统通常由、、、以及计算机控制管理系统组成。
二、单项选择题1.反求工程形体几何参数获得的破坏性测量方法是()a. 三坐标测量b. 光学测量c. 自动断层扫描2.高速加工机床的进给系统机构大多采用()a. 直线电机b. 滑动丝杠传动机构c. 摩擦传动机构3.不适合用精密与超精密机床的进给系统的方式为()a. 滚珠丝杠螺母机构b. 压电陶瓷驱动装置c. 弹性变形机构5. ERP的含义是()a. 制造资源计划b. 物料需求计划c. 企业资源计划d. 产品数据管理9.FMS非常适合()a. 大批大量生产方式b. 品种单一、中等批量生产方式c. 多品种、变批量生产方式10.在进行纳米级测量非导体的零件表面形貌时,常采用的测量仪器为()a. 光学显微镜b. 扫描隧道显微镜c. 原子力显微镜12.不同的材料高速切削速度范围是不同的,其中铝合金和钛的高速切削速度范围是()a. 1000~5000m/min ;1000~3000m/min;b. 500~2000m/min ; 800~3000m/min;c. 1000~7000m/min ; 100~1000m/min;13.光刻加工的工艺过程为:()a. ①氧化②沉积③曝光④显影⑤还原⑦清洗b. ①氧化②涂胶③曝光④显影⑤去胶⑦扩散c. ①氧化②涂胶③曝光④显影⑤去胶⑦还原14.光刻加工采用的曝光技术中具有最高分辨率的是()a. 电子束曝光技术b. 离子束曝光技术c. X射线曝光技术15.硅微体刻蚀加工和硅微面刻蚀加工的区别在于()a. 体刻蚀加工对基体材料进行加工,而面刻蚀加工不对衬底材料进行加工;b. 体刻蚀加工不对基体材料进行加工,而面刻蚀加工对衬底材料进行加工;c. 体刻蚀加工可获得高纵横比的结构,而面刻蚀加工只能获得较低纵横比的结构;16.工业机器人有多种分类方式,下列不属于按驱动方式分类的是()a.气压传动机器人;b. 液压传动机器人;c. 电器传动机器人;d.智能机器人;17.高速切削使用的刀具材料有很多种,其中与金属材料亲和力小,热扩散磨损小,高温硬度优于硬质合金,当韧性较差的是()a. 陶瓷刀具;b.; 聚晶金刚石刀具c.立方氮化硼刀具;22.磨削铸铁时,采用下列哪种磨料较好()a.刚玉;b.人造金刚石c.立方氮化硼23.微细加工技术中的刻蚀工艺可分为下列哪两种()a离子束刻蚀、激光刻蚀 b. 干法刻蚀、湿法刻蚀 c. 溅射加工、直写加工24.LIGA技术中不包括的工艺过程为()a.涂胶b.同步辐射X射线深层光刻c.电铸成形d.注塑25. 衡量机器人技术水平的主要指标是()a.自由度b. 工作空间c. 提取重力d.运动速度26. 在机器人控制系统中下列不属于按其控制方式划分的是()a.集中控制方式b. 主从控制方式c.分散控制方式d.点位式30. 微细加工主要指微细尺寸零件大小在________以下,加工精度为________的加工。
第32卷第10期中国机械工程V o l .32㊀N o .102021年5月C H I N A M E C HA N I C A LE N G I N E E R I N Gp p.1181G1190几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响席静谣㊀周长光㊀冯虎田㊀张鲁超南京理工大学机械工程学院,南京,210094摘要:建立了一种考虑几何误差(滚珠尺寸误差㊁丝杠导程误差和滚道齿形误差)和倾覆力矩的双螺母滚珠丝杠副载荷分布模型;通过试验测得4010型滚珠丝杠副的力与位移变形曲线,验证了理论模型的正确性;通过仿真分析研究了轴向外载荷㊁几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响.研究结果表明:轴向外载荷一定时,倾覆力矩会导致双螺母滚珠丝杠副的载荷分布迅速变差;滚珠尺寸误差和滚道齿形误差会使双螺母滚珠丝杠副中滚珠的受载显著增大或减小;由于丝杠轴向误差累计的作用,导程误差会使双螺母滚珠丝杠副中一侧螺母受载增大,另一侧螺母受载减小;在误差大小一定的情况下,导程误差对载荷分布的影响程度大于尺寸误差和齿形误差,即双螺母滚珠丝杠副的载荷分布对导程误差的敏感度更高.关键词:双螺母滚珠丝杠副;载荷分布;滚珠几何误差;倾覆力矩中图分类号:T H 122D O I :10.3969/j .i s s n .1004 132X.2021.10.006开放科学(资源服务)标识码(O S I D ):L o a dD i s t r i b u t i o no fD o u b l eN u t B a l l S c r e w sw i t hC o n s i d e r a t i o no f G e o m e t r i cE r r o r s a n dO v e r t u r n i n g Mo m e n t X I J i n g y a o ㊀Z HO U C h a n g g u a n g㊀F E N G H u t i a n ㊀Z H A N GL u c h a o S c h o o l o fM e c h a n i c a l E n g i n e e r i n g ,N a n j i n g U n i v e r s i t y o f S c i e n c e a n dT e c h n o l o g y ,N a n j i n g,210094A b s t r a c t :Al o a dd i s t r i b u t i o nm o d e l o f d o u b l en u t b a l l s c r e w sw a s e s t a b l i s h e db y c o n s i d e r i n g th e g e o m e t r i c e r r o r s (b a l l s i z e e r r o r ,l e a de r r o ra n dr a c e w a yp r o f i l ee r r o r )a n do v e r t u r n i n g mo m e n t .T h e f o r c e a n dd i s p l a c e m e n td e f o r m a t i o nc u r v e so f a t y p i c a l 4010b a l l s c r e w w e r e m e a s u r e dt ov e r i f y th e c o r r e c t n e s s o f t h e t h e o r e t i c a lm o d e l .T h e e f f e c t s o f a x i a l l o a d s ,g e o m e t r i c e r r o r s a n do v e r t u r n i n g mo Gm e n t o n t h e l o a d d i s t r i b u t i o n o f d o u b l e n u t b a l l s c r e ww e r e s t u d i e d b y s i m u l a t i o n a n a l ys i s .T h e r e s u l t s s h o wt h a tw h e n t h e a x i a l l o a d s a r e o f a c o n s t a n t ,t h e o v e r t u r n i n g m o m e n tm a y ca u s e t h e l o a d d i s t r ib u Gt i o no f d o u b l en u tb a l l sc r e w s t ode t e r i o r a t er a p i d l y .T h eb a l l s i z ee r r o r sa n dr a c e w a yp r of i l ee r r o r s m a yl e a d t o t h e l o a d s o f t h e b a l l s e i t h e r i n c r e a s e o r d e c r e a s e .D u e t o t h e a c c u m u l a t i o no f t h e e r r o r s i n t h e s c r e wa x i a l d i r e c t i o n ,t h e l e a d e r r o r sm a yl e a d t o t h e i n c r e a s e o f t h e l o a dw i t h i n o n ew i d e n u tw h i l e t h e d e c r e a s e o f t h e l o a dw i t h i n t h e o t h e r s i d en u t .W h e n t h e e r r o r s i z e sk e e p co n s t a n t ,t h e i n f l u e n c e s o f l e a d e r r o r s o n t h e l o a d d i s t r i b u t i o n i s g r e a t e r t h a n t h a t o f t h e b a l l s i z e e r r o r s a n d r a c e w a y pr o f i l e e r Gr o r s ,n a m e l yt h e l o a dd i s t r i b u t i o n o f d o u b l e n u t b a l l s c r e w s i sm o r e s e n s i t i v e t o t h e l e a d e r r o r s .K e y wo r d s :d o u b l en u t b a l l s c r e w ;l o a dd i s t r i b u t i o n ;b a l l g e o m e t r i c e r r o r ;o v e r t u r n i n g m o m e n t 收稿日期:20200526基金项目:国家科技重大专项(2019Z X 04010001)0㊀引言滚珠丝杠副是实现力与力矩转换的传动装置,具有承载能力强㊁刚性高㊁定位精度高㊁使用寿命长等[1]优良特性,近年来被广泛应用于航空航天㊁军工核电等领域.滚珠丝杠副载荷分布是直接影响承载能力和刚性的关键因素,对其进行研究与优化可有效提高滚珠丝杠副的机械性能[2].滚珠丝杠副的结构参数与材料特性决定了其载荷分布情况,但由于加工过程存在因制造精度㊁热变形等因素带来的滚珠尺寸误差㊁丝杠导程误差以及滚道齿形误差等几何误差,所以每个滚珠实际受力情况各不相同[3].在滚珠丝杠副的使用过程中,自由端的移动(固定支撑安装方式)会导致丝杠受到额外的倾覆力矩,同样会造成滚珠受力不均的现象[4].因此,研究几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响具有重要意义.国内外学者在滚珠丝杠副摩擦[5G6]㊁温升预测[7]㊁寿命预测[8G9]和健康诊断[10G12]等方面进行了1811大量研究.在滚珠丝杠副载荷分布研究方面,W E I 等[13]建立了滚珠丝杠副动力学模型并分析了转速对接触力的影响,但是模型中假设所有滚珠受力相同;C H E N 等[14]得到了基于完整滚动体的单螺母滚珠丝杠副的载荷分布,结果表明每个滚珠的法向接触力是逐渐递减的.L I N [15]采用数值计算的方法对滚珠丝杠副的受力情况进行仿真,发现每个滚珠的法向力各不相同,但其变化趋势并不是单纯的递减,而是存在一定的波动情况.B E R T O L A S O 等[16]采用光测弹性仪与标记追踪技术对承载状态下每个滚珠的位移量进行监测,并以此计算出其法向接触力,试验结果表明滚珠的法向接触力逐渐减小.L I U 等[17]建立了一种考虑倾覆力矩的单螺母载荷分布模型,并分析了螺母位置对载荷分布的影响.以上研究在计算滚珠丝杠副载荷分布时未考虑误差的影响,因此模型在应用时会出现一定偏差.M E I 等[18]在考虑丝杠和螺母的变形情况下,分析了几何误差对单螺母滚珠丝杠副的载荷分布的影响.Z H E N 等[19]和Z H A O 等[20]建立了轴向载荷和力矩作用下的单螺母滚珠丝杠副载荷分布模型,并分析了滚珠尺寸误差对丝杠副疲劳寿命的影响.L I N 等[21]对单螺母滚珠丝杠副载荷分布的研究考虑了几何误差带来的影响,但计算过程中只针对一个滚珠施加了几何误差,误差值并不随机,且误差被直接转化为滚珠尺寸的变化,计算的准确性仍需验证.以上研究虽然考虑了尺寸误差对单螺母滚珠丝杠副载荷分布的影响,但是计算过程中将导程误差㊁齿形误差转化为滚珠尺寸误差,且误差值并不随机,因而计算结果与实际情况仍有差异.综上所述,目前关于滚珠丝杠副载荷分布的研究主要集中在单螺母,对双螺母载荷分布的研究则相对较少.为此,本文建立了一种考虑几何误差(滚珠尺寸误差㊁丝杠导程误差和滚道齿形误差)和倾覆力矩的双螺母滚珠丝杠副载荷分布模型.1㊀载荷分布模型的建立本文在建立双螺母滚珠丝杠副载荷分布模型时,作如下假设:①滚珠与丝杠㊁螺母滚道的接触变形均在弹性范围内;②丝杠和螺母滚道的曲率中心与滚珠的中心在同一直线上;③忽略滚珠与滚道之间的摩擦.如图1所示,在一端固定一端支撑的安装方式下,滚珠丝杠副会受到倾覆力矩的作用,导致丝杠轴线与螺母轴线存在一定的偏角.为了便于分析,假定两个螺母固定,且丝杠顺时针方向倾斜为正,F a 是轴向外载荷,F p 是预紧力,T 是丝杠受到的倾覆力矩,θᶄ是丝杠轴线与螺母轴线之间的倾斜角.滚珠与滚道的接触状态见图2,可知,螺母A 和螺母B 分别受到轴向外载荷和预紧力的共同作用,其轴向力与每颗滚珠的法向接触载荷之间的关系为F Aa=ðNi =1PA n is i n βAi c o s λ(1)F Ba=ðNi =1PB n is i n βBi c o s λ(2)图1㊀在倾覆力矩作用下丝杠与螺母的相对位置图F i g .1㊀D i a g r a mo f t h e r e l a t i v e p o s i t i o no f t h e s c r e wa n dn u t u n d e r t h e o v e r t u r n i n g mo m e nt 图2㊀轴向载荷较小时滚珠与滚道的接触状态F i g .2㊀T h e c o n t a c t s t a t e o f t h eb a l l a n d t h e r a c e w a y un d e r t h e s m a l l a x i a l l o a d2811 中国机械工程第32卷第10期2021年5月下半月式中,F A a ㊁F Ba分别为螺母A 和螺母B 受到的轴向力;P A n i ㊁P B n i 分别为滚珠与螺母A ㊁螺母B 滚道的法向接触载荷;βA i ㊁βB i 分别为滚珠与螺母A ㊁螺母B 滚道接触点处的接触角;λ为丝杠的螺旋升角;N 为螺母A 与螺母B 的滚珠个数.未施加轴向外载荷时,两个螺母仅受预紧力作用,此时滚珠所受法向接触载荷分别为P A n i 0=P A s i 0=F pN s i n β0c o s λ(3)P B n i 0=P B s i 0=F p N s i n β0c o s λ(4)式中,P A n i 0㊁P A s i 0㊁P B n i 0㊁P B s i 0为仅在预紧力作用下各个滚珠在丝杠㊁螺母接触点处的法向接触载荷;β0为初始接触角,β0=45ʎ.由赫兹弹性接触理论可知,滚珠与丝杠或螺母滚道的接触区域呈椭圆形,滚珠法向接触载荷与滚珠变形量δi 0之间的关系为P A s i 0=P B s i 0=K δ3/2i 0(5)K =[2k s (e )πm a s3132(3E ᶄ)2ðρs +2k n (e )πm a n3132(3E ᶄ)2ðρn ]-32(6)1E ᶄ=1-μ21E 1+1-μ22E 2(7)式中,k s (e )㊁k n (e )分别为滚珠与丝杠和螺母接触椭圆的第一椭圆积分;m a s ㊁m a n 分别为滚珠与丝杠㊁螺母接触椭圆的短半轴系数;E ᶄ为等效弹性模量;ρs ㊁ρn 分别为两个接触椭圆的主曲率;μ1㊁μ2分别为两个接触椭圆的有效泊松比;E 1㊁E 2分别为两个接触椭圆的有效弹性模量.在轴向外载荷的作用下,垫片会产生相应的轴向位移和轴向变形,轴向位移量用x m 表示,轴向变形量δm =F ak m(8)其中,k m 为垫片的刚性系数,则垫片的位移量及变形量在法平面上的横向位移为(x m +δm )c o s λ.由于倾覆力矩的存在,丝杠轴线与螺母轴线存在一定的偏角,故在沿着螺母轴线的不同横截面处,每颗滚珠的径向位移是不同的.滚珠的位置角表示如图3所示,在下面的讨论中均选定该情况下的径向位移为正值.假定第一颗滚珠的初始位置角为σ,相邻两颗滚珠球心的角度为φ,则任意一颗滚珠的位置角ψi =(i -1)φ+σ(9)假设螺母中滚珠循环圈数为Z ,丝杠的螺距为L p ,则φ=(2πZ )/N .ΔL 为相邻两颗滚珠的轴向距离,则ΔL =Z L p /N .根据图3所示的几何位置关系,可以得到螺母A 和螺母B 中任意一颗滚珠的径向位移分别为(a)三维视图(b)轴向视图图3㊀滚珠位置角F i g .3㊀T h eb a l l p o s i t i o na n gl e δA r i =[(i -1)ΔL s i n θᶄ+δAr 1]c o s ψi (10)δB r i =[(i -1)ΔL s i n θᶄ+δB r 1]c o s ψi(11)按照之前的假定,螺母滚道中心O n 视为在空间固定,则在轴向外载荷和倾覆力矩作用下,滚珠球心以及丝杠和螺母滚道曲率中心的几何位置变化如图4所示.其中,P 点与Q 点分别为轴向外载荷和倾覆力矩作用前滚珠与丝杠和螺母滚道的接触点,P ᶄ点和Q ᶄ点分别为轴向外载荷和倾覆力矩作用后滚珠与丝杠和螺母滚道的接触点,O n ㊁O s 和O b 分别为轴向外载荷和倾覆力矩作用图4㊀滚珠与丝杠㊁螺母滚道曲率中心的位置关系变化图F i g .4㊀T h e p o s i t i o n a l r e l a t i o n s h i p c h a n g e d i a gr a mo f t h e c u r v a t u r e c e n t e r o f t h eb a l l ,s c r e wa n dn u t r a c e w a y3811 几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响 席静谣㊀周长光㊀冯虎田等前的螺母滚道曲率中心㊁丝杠滚道曲率中心和滚珠球心,Oᶄs和Oᶄb分别为轴向外载荷和倾覆力矩作用后的丝杠滚道曲率中心和滚珠球心,βi为轴向外载荷和倾覆力矩作用后的接触角.丝杠在法平面的旋转角θ与在轴平面的旋转角θᶄ不同,根据空间几何关系,其相互转化关系为t a nθ=t a nθᶄc o sλ(12)在滚珠没有受到外加轴向载荷和倾覆力矩的情况下,各滚珠接触点处丝杠滚道中心与螺母滚道中心的距离M0=O n O s=r n+r s-2r b(13)式中,r n㊁r s㊁r b分别为螺母滚道曲率半径㊁丝杠滚道曲率半径和滚珠半径.在螺母仅受预紧力的情况下,各滚珠接触点处丝杠滚道中心与螺母滚道中心的距离M=M0+δi0(14)在轴向外载荷和倾覆力矩作用后,螺母A中各个滚珠接触点处丝杠滚道中心与螺母滚道中心的距离O n Oᶄs={(M c o sβ0+δA r i)2+[M s i nβ0+(x m+δm)c o sλ+θR∗i]2}1/2(15) R∗i=r m+(r s-r b)c o sβ0式中,R∗i为丝杠滚道中心的旋转半径;r m为丝杠的公称半径.螺母A中各滚珠的接触变形δA i=O n Oᶄs-O n O s={(M c o sβ0+δA r i)2+㊀[M s i nβ0+(x m+δm)c o sλ+θR∗i]2}1/2-M0(16)螺母A中各滚珠的接触角㊀βA i=a r c s i n(M s i nβ0+(x m+δm)c o sλ+θR∗iO n Oᶄs)(17)同理,螺母B中各个滚珠接触点处丝杠滚道中心与螺母滚道中心的距离O n Oᵡs={(M c o sβ0+δB r i)2+㊀㊀㊀[M s i nβ0-(x m+δm)c o sλ+θR∗i]2}1/2(18)螺母B中各滚珠的接触变形δB i=O n Oᵡs-O n O s={(M c o sβ0+δB r i)2+㊀[M s i nβ0-(x m+δm)c o sλ+θR∗i]2}1/2-M0(19)螺母B中各滚珠的接触角㊀βB i=a r c s i n(M s i nβ0-(x m+δm)c o sλ+θR∗iO n Oᵡs)(20)根据赫兹弹性接触理论,螺母A和螺母B中每颗滚珠法向接触载荷与变形量之间的关系为P A n i=Kδ3/2A i(21)P B n i=Kδ3/2B i(22)当丝杠受到倾覆力矩时,相对于螺母轴线的力矩平衡方程为T=ðN i=1P n i s i nβi c o sλ(r m-r b)c o sψi(23)联立式(1)㊁式(17)㊁式(21)㊁式(23),可以得到螺母A受到的力和力矩的平衡方程:F A a=ðN i=1{Kδ3/2A i[M s i nβ0+(x m+δm)c o sλ+θR∗i]c o sλ/O n Oᶄs}T A=ðN i=1{Kδ3/2A i[M s i nβ0+(x m+δm)c o sλ+θR∗i]c o sλ(r m-r b)c o sψi/O n O s}üþýïïïïïïï(24)联立式(1)㊁式(20)㊁式(22)㊁式(23),得到螺母B受到的力与力矩的平衡方程:F B a=ðN i=1{Kδ3/2B i[M s i nβ0-(x m+δm)c o sλ+θR∗i]c o sλ/O n Oᵡs}T B=ðN i=1{Kδ3/2B i[M s i nβ0-(x m+δm)c o sλ+θR∗i]c o sλ(r m-r b)c o sψi/O n Oᵡs}üþýïïïïïïï(25)螺母A与螺母B两者之间的力与力矩的平衡关系为F a=F A a-F B aT=T A+T B}(26)如图5所示,双螺母滚珠丝杠副的几何误差主要包括滚珠的尺寸误差㊁丝杠的导程误差以及丝杠和螺母滚道的齿形误差三种.由图5可知,丝杠导程误差可等效看成丝杠沿轴向产生变形,则螺母A和螺母B中每颗滚珠的变形量如下:δᶄA i=O n Oᶄs-O n O s+E A i+e A i={(M c o sβ0+δA r i)2+[M s i nβ0+(x m+δm+E s)c o sλ+θR∗i]2}1/2-M0+E A i+e A i(27)δᶄB i=O n Oᵡs-O n O s+E B i+e B i={(M c o sβ0+δB r i)2+[M s i nβ0-(x m+δm+E s)c o sλ+θR∗i]2}1/2-M0+E B i+e B i(28)式中,E A i㊁E B i分别为螺母A和螺母B中任意滚珠的随机尺寸误差;e A i㊁e B i分别为螺母A和丝杠滚道以及螺母B 和丝杠滚道的齿形误差;E s为丝杠的导程误差.图5㊀三种几何误差下滚珠与滚道的位置关系图F i g.5㊀P o s i t i o n r e l a t i o n s h i p d i a g r a mo fb a l l a n dr a c e w a y u n d e r t h r e e g e o m e t r i c e r r o r s螺母A和螺母B中每颗滚珠与滚道接触点处的接触角修正为βᶄA i=a r c s i n(M s i nβ0+(x m+δm+E s)c o sλ+θR∗iO n Oᶄs+E A i+e A i)(29)4811中国机械工程第32卷第10期2021年5月下半月βᶄB i =a r c s i n (M s i n β0-(x m +δm +E s )c o s λ+θR ∗i O n O ᶄs +E B i +e B i)(30)联立式(24)~式(30),得到几何误差和倾覆力矩作用下螺母A 和螺母B 受到的力和力矩平衡方程:F A a=ðNi =1{K (δA i +E A i +e A i )32[M s i n β0+(x m +δm +E s )c o s λ+θR ∗i ]c o s λ/(O n O ᶄs +E A i +e A i)}T A=ðNi =1{K (δA i +E A i +e A i )32[M s i n β0+(x m +δm +E s )c o s λ+θR ∗i ]c o s λ(r m -r b )c o s ψi/(O n O ᶄs +E A i +e A i )}üþýïïïïïïïï(31)F Ba=ðNi =1{K (δB i +E B i +e B i )32[M s i n β0-(x m +δm +E s )c o s λ+θR ∗i ]c o s λ/(O n O ᶄs +E B i +e B i )}T B=ðNi =1{K (δB i +E B i +e B i )32[M s i n β0-(x m +δm +E s )c o s λ+θR ∗i ]c o s λ(r m -r b )c o s ψi/(O n O ᶄs +E B i +e B i )}üþýïïïïïïïï(32)整个滚珠的受载模型可以通过MA T L A B 中牛顿迭代法工具箱计算得到,通过计算每颗滚珠的受力就可以分析出整个双螺母滚珠丝杠副的载荷分布情况.2㊀实验验证使用南京理工大学自主研发的轴向静刚度试验台测量双螺母滚珠丝杠副的轴向变形量,将测量结果与理论计算结果进行对比分析,以验证载荷分布模型的正确性.实验过程中采用 螺母固定 的测量方式,对滚珠丝杠旋转现象采取防转措施,并使用具有旋转补偿功能的新型滚珠丝杠副轴向静刚度测量装置,如图6所示.本实验选用的三个厂家生产的4010型滚珠丝杠副的相关参数值见表1,精度等级为3级,预紧方式为双螺母垫片预紧,动态摩擦力矩为(1.634ʃ0.0817)N m .表1㊀C U T G2平台轴承参数表(实验)T a b .1㊀B a l l s c r e w pa r a m e t e r t ab l e (e x pe r i m e n t a l )厂家A 厂家B 厂家C 滚珠半径r b (mm )3.1753.1753.175公称半径r m (mm )202020螺旋升角λ(ʎ)4.554.554.55初始接触角β0(ʎ)454545导程L p (mm )101010额定动载荷C a (k N )45.7633.1241.69循环圈数Z 4.753.754螺母外径D (mm )827082丝杠或螺母适应度0.5400.5550.530图6㊀滚珠丝杠副轴向静刚度测量装置F i g .6㊀A x i a l s t a t i c s t i f f n e s sm e a s u r i n g de v i c e of b a l l s c r e w ㊀㊀移动横梁下方连接压力传感器,当丝杠受力时,压力传感器可以实时获取丝杠的受力情况,刚度测量装置中安装4个接触位移传感器(型号:P r e t e c 2940N ,分辨力为0.1μm )记录滚珠丝杠副轴向变形量.实验前,以滚珠丝杠副额定动载荷C a 的30%为外加载荷,对滚珠丝杠副预压3次,消除测量装置之间的间隙.实验时,移动横梁以0.2mm /m i n 的速度对丝杠进行缓慢加载,外加载荷F a 达到0.3C a (取整)后进行卸载,直到外加载荷为0.丝杠测量基准上,3个轴线方向的接触式位移传感器测得的丝杠轴向变形量分别为d 1㊁d 2㊁d 3;旋转方向上,接触位移传感器测得的丝杠相对于螺母的旋转变形量为d 4.滚珠丝杠副中丝杠与螺母间的相对变形量d =(d 1+d 2+d 3)/3-L p d 4/(2πL )(L 为测量旋转变形量的位移传感器接触点到丝杠轴线的距离).实验需重复测量3次以上(确保每根丝杠多次测量的数据重复性较好,如某次测量数据明显区别于其他各次测量数据,则视为异常,剔除该次测量数据,分析原因并重新补测).为保证实验结果的准确性,设定预加载力为0.9k N ,当加载力不大于0.9k N 时,数据不参与轴向变形量计算.在施加载荷大于起始载荷而小于预设最大载荷的加载或卸载过程中,根据各传感器在各数据采集点的测量值相对于预加载时测量值的变动量,计算得到相对于预加载时的载荷及变形的变动量.以载荷增量为横坐标㊁相对变形量为纵坐标,绘制点图.利用MA T L A B 中牛顿迭代法工具箱计算该滚珠丝杠副在不同轴向外载荷作用下的轴向变形量,计算结果与实验结果对比如图7所示.5811 几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响席静谣㊀周长光㊀冯虎田等㊀㊀㊀㊀㊀(a)厂家A㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(b)厂家B㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(c)厂家C图7㊀实验结果与理论结果对比F i g.7㊀C o m p a r i s o no f e x p e r i m e n t a l r e s u l t s a n d t h e o r e t i c a l r e s u l t s㊀㊀由于所选滚珠丝杠副的精度等级为3级,滚珠精度等级为G10,故根据丝杠出厂设置参数表和I S O3408G3,以及误差服从正态分布,可设定滚珠的随机尺寸误差为N(0,(0.5/6)2),滚道的随机齿形误差为N(0,(4/6)2),丝杠的导程误差为N(0,(2.5/6)2).可以看出,由于不同滚珠尺寸误差和滚道齿形误差数据的随机性,最终得到的加载变形曲线并不是一个固定值,而是在某一范围内波动的变化量,图7中用剖面线标示.厂家A㊁B㊁C轴向变形量的理论值与实验值的最大相对偏差分别为17%㊁18%和6%,原因是本文模型计算的是接触刚性,而实验结果包含了丝杠㊁螺母的变形以及扭转刚性等,故理论值会相对实验值偏小.由于实验设备和条件的限制,无法测量倾覆力矩,故本文建立的双螺母滚珠丝杠副载荷分布模型可在一定程度上有效计算滚珠的受力.3㊀结果讨论为了研究轴向外载荷㊁几何误差㊁倾覆力矩对双螺母滚珠丝杠副载荷分布的影响,本节选用陕西汉江机床有限公司生产的F N系列4010型滚珠丝杠副进行MA T L A B仿真分析,滚珠丝杠副的具体相关参数见表2.该滚珠丝杠副的额定动载荷为30k N,采用外循环方式,丝杠和螺母材料表2㊀滚珠丝杠副参数表(仿真)T a b.2㊀B a l l s c r e w p a r a m e t e r t a b l e(s i m u l a t i o n)参数数值滚珠半径r b(mm)2.977滚道半径r s(mm)3.155公称半径r m(mm)20螺旋升角λ(ʎ)4.55初始接触角β0(ʎ)45导程L p(mm)10预紧力F p(k N)6循环圈数Z6受载滚珠个数N126泊松比μ1㊁μ20.3弹性模量E1㊁E2(G P a)205均为G C r15.在滚珠丝杠副的A㊁B两螺母中共有138颗滚珠,由于返向器中的12颗滚珠不受载,故A㊁B 螺母中各有63颗滚珠受载.3.1㊀轴向外载荷对载荷分布的影响当丝杠受到10k N mm的倾覆力矩时,双螺母滚珠丝杠副在不同轴向外载荷下的载荷分布如图8所示.可以看出,轴向外载荷从6k N增加到20k N时,滚珠丝杠副中滚珠受到的最大法向接触载荷由255.51N增大到489.58N,最小法向接触载荷由73.02N减小到0,且丝杠副中最大与最小法向接触载荷的差值由182.49N增大到489.58N.由此可知,随着轴向外载荷的增加,螺母A中滚珠与滚道的法向接触载荷增大,螺母B 中滚珠与滚道的法向接触载荷减小,且轴向外载荷的增加会导致螺母A和螺母B距离垫片相同位置处滚珠的受力差值变大.此现象的原因在于轴向外载荷的存在会增大螺母A受到的轴向载荷,使螺母A中滚珠受到的法向接触载荷相应增大,而轴向外载荷的存在会适当抵消螺母B受到的轴向载荷,使螺母B中滚珠受到的法向接触载荷相应减小.图8㊀不同轴向外载荷下双螺母滚珠丝杠副的载荷分布图F i g.8㊀L o a dd i s t r i b u t i o nd i a g r a mo f d o u b l e n u t b a l ls c r e wu n d e r d i f f e r e n t a x i a l e x t e r n a l l o a d s6811 中国机械工程第32卷第10期2021年5月下半月由MA T L A B 计算可知,当轴向外载荷增大到18.3k N 时,螺母B 开始出现滚珠不受载现象,此时第54颗滚珠受到的法向接触载荷为0.当继续增加轴向外载荷至23.6k N 时,螺母B 中的63颗滚珠正好全部不受载,此时滚珠与滚道完全脱开,形成卸载状态,造成滚珠丝杠副的失效.在这种状态下,滚珠与滚道之间的接触处于极其不稳定的状态,可能会导致滚珠丝杠副中的油膜破裂㊁滚珠与滚道之间的接触角改变,从而加剧磨损㊁降低寿命.由此推断,该双螺母滚珠丝杠副在10k N mm 倾覆力矩的作用下,可以承受的最大工作载荷为23.6k N .3.2㊀倾覆力矩对载荷分布的影响低载(轴向外载荷为6k N )状态时双螺母滚珠丝杠副在不同倾覆力矩下的载荷分布如图9所示.可以看出,倾覆力矩的增加会导致滚珠丝杠副中93.65%的滚珠受到的法向接触载荷增大.在螺母A ㊁B 载荷分布曲线的第一个波谷处,第11~16颗滚珠的受载随着倾覆力矩的增加而增大;至第二个波谷处,第31~36颗滚珠的受载几乎不受倾覆力矩的影响;在最后一个波谷处,第52~55颗滚珠的受载随着倾覆力矩的增加而略微减小.选用一侧螺母的(P i ,m a x -P i ,m i n )/P i ,m i n 来表征载荷分布曲线的波动幅度,则当倾覆力矩从10k N mm 增加到30k N mm 时,螺母A 的波动幅度从28.18%增大到88.55%,螺母B 的波动幅度从57.89%增大到186.53%.由此推断,倾覆力矩越大,螺母A ㊁B 中滚珠受到的法向接触载荷的波动幅度越大,相邻滚珠间的受载越不均匀,故在实际应用中,应尽量避免倾覆力矩的存图9㊀不同倾覆力矩下双螺母滚珠丝杠副的载荷分布图F i g .9㊀L o a dd i s t r i b u t i o nd i a gr a mo f d o u b l e n u t b a l l s c r e wu n d e r d i f f e r e n t o v e r t u r n i n g mo m e n t s 在,否则会由于滚珠受力不均导致滚珠丝杠副的刚性降低,寿命缩短.3.3㊀几何误差对载荷分布的影响由图5可以看出,滚珠的尺寸误差与滚道的齿形误差对滚珠丝杠副载荷分布的影响规律相似,故在后文中仅分析以上两种误差之和对双螺母滚珠丝杠副载荷分布的影响.在双螺母滚珠丝杠副受到10k N mm 的倾覆力矩(轴向外载荷为6k N )的情况下,利用MA T L A B 随机产生误差范围分别为ʃ1μm 和ʃ2μm 的两组数据,绘制滚珠丝杠副的载荷分布如图10所示.由于误差数据的随机性,载荷分布曲线不再是平滑的曲线,而是呈现在一定范围内无规律上下波动的趋势,因此选用标准差来反映载荷分布的不均匀程度.当误差从ʃ1μm 增大到ʃ2μm 时,螺母A 和螺母B 中滚珠受载的标准差分别从25.02和18.57增大到42.13和31.27,且滚珠丝杠副的最大法向接触载荷与最小法向接触载荷的差值从209.70N 增大到了268.79N .可以看出,由于误(a )ʃ1μm误差(b )ʃ2μm 误差图10㊀误差分别为ʃ1μm 和ʃ2μm 时的载荷分布图F i g .10㊀L o a dd i s t r i b u t i o nd i a gr a m w h e n t h e e r r o r i s ʃ1μma n d ʃ2μm7811 几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响席静谣㊀周长光㊀冯虎田等差的存在,每颗滚珠的尺寸不再相同,导致滚珠与滚道之间的接触载荷沿着无误差时的载荷分布曲线上下波动,且误差范围越大,波动幅值越大,载荷分布越不均匀.因此,选用高精度的滚珠可有效改善双螺母滚珠丝杠副中载荷分布不均的现象,降低磨损,延长使用寿命.与前面尺寸误差和齿形误差的条件相同,当双螺母滚珠丝杠副受到10k N mm 的倾覆力矩(轴向外载荷为6k N )时,丝杠导程在1μm 误差下的载荷分布如图11所示.该误差下滚珠丝杠副的最大法向接触载荷与无误差情况相比,从255.51N 增大到了280.97N ,最小法向接触载荷从70.02N 减小到了57.29N .可以看出,丝杠导程误差使螺母A 中滚珠与滚道的法向接触载荷增大,螺母B 中滚珠与滚道的法向接触载荷减小,且螺母A ㊁B 距离垫片相同位置处滚珠的受力差值增大.图11㊀丝杠导程误差下双螺母滚珠丝杠副的载荷分布图F i g .11㊀L o a dd i s t r i b u t i o nd i a gr a mo f d o u b l e n u t b a l l s c r e wu n d e r l e a d e r r o r o f s c r e w三种误差分别作用和共同作用在双螺母滚珠丝杠副上的载荷分布如图12所示.从图12a 中可以看出,在ʃ1μm 尺寸误差和齿形误差的影响下,滚珠丝杠副的最大法向接触载荷与最小法向接触载荷之差为209.7N ;在ʃ1μm 导程误差的影响下,滚珠丝杠副的最大法向接触载荷与最小法向接触载荷之差为223.68N .因此,在滚珠丝杠副受载不均方面,误差大小相同时导程误差的影响大于尺寸误差和齿形误差.当分别考虑螺母A 和螺母B 滚珠的受载情况时,可以发现,螺母A 中滚珠在导程误差下的受载普遍大于滚珠在尺寸误差和齿形误差下的受载,螺母B 中滚珠在导程误差下的受载普遍小于滚珠在尺寸误差和齿形误差下的受载.图12b 显示了三种误差共同作用在双螺母滚珠丝杠副上的载荷分布,可以看出,与无误差情况相比,此时滚珠丝杠副的最大法向接触载荷由255.51N 增大到了299.78N ,最小法向接触载荷由73.02N 减小到42.83N ,故ʃ1μm 尺寸误差和齿形误差以及ʃ1μm 导程误差的共同作用使滚珠丝杠副中滚珠的最大法向接触载荷与最小法向接触载荷的差值增大了40.80%.(a)三种误差分别作用(b)三种误差共同作用图12㊀三种误差分别作用和共同作用下双螺母滚珠丝杠副的载荷分布图F i g .12㊀T h e l o a dd i s t r i b u t i o nd i a g r a mo f t h e d o u b l e n u t b a l l s c r e wu n d e r t h e t h r e e k i n d s o f e r r o r ss e p a r a t e l y a n d t o ge t h e r 3.4㊀综合分析双螺母滚珠丝杠副的载荷分布在轴向外载荷㊁几何误差和倾覆力矩的共同作用下,双螺母滚珠丝杠副的载荷分布三维图见图13和图14.图13为在低载(轴向外载荷为6k N )㊁中载(轴向外载荷为12k N )和重载(轴向外载荷为20k N )下载荷随倾覆力矩变化三维图,此时导程误差为ʃ1μm ,尺寸误差和齿形误差之和为ʃ1μm .可以看出,由于几何误差的存在,导致滚珠的载荷分布波动极大,在相同的轴向外载荷条件下,即使倾覆力矩从5k N mm 增大到30k N mm ,也仍有部分滚珠受到的法向接触载荷与在5k N mm 倾覆力矩下部分滚珠受到的8811 中国机械工程第32卷第10期2021年5月下半月法向接触载荷相差不大,故几何误差对滚珠载荷分布的影响较大,会抵消部分倾覆力矩带来的影响.图14为在低载㊁中载和重载下载荷随几何误差变化三维图.此时导程误差为1μm 的定值,倾覆力矩为10k N mm .可以看出,滚珠尺寸误差和滚道齿形误差之和从ʃ1μm 增大到ʃ4μm时,螺母B 中部分滚珠受到的法向接触载荷显著增大或减小,在重载情况下更容易出现第一颗滚珠不受载㊁与滚道脱离的现象,但也可减缓螺母B中所有滚珠与滚道脱离,即卸载状态的发生.㊀㊀㊀㊀㊀(a )低载㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(b )中载㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(c)重载图13㊀低载㊁中载和重载下载荷随倾覆力矩变化三维图F i g .13㊀T h e 3Dd i a g r a mo f t h e l o a dw i t h t h e o v e r t u r n i n g m o m e n t u n d e r l o wl o a d ,m e d i u ml o a da n dh e a v yl o ad ㊀㊀㊀㊀㊀(a )低载㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(b )中载㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(c)重载图14㊀低载㊁中载和重载下载荷随几何误差变化三维图F i g .14㊀T h e 3Dd i a g r a mo f t h e l o a dw i t h g e o m e t r i c e r r o r u n d e r l o wl o a d ,m e d i u ml o a da n dh e a v yl o a d 4㊀结论(1)倾覆力矩一定时,增大轴向外载荷会使螺母A 中滚珠受载增大,螺母B 中滚珠受载减小,且会导致螺母A 和螺母B 距离垫片相同位置处滚珠的受力差值变大.当轴向外载荷增大到一定程度时,螺母B 开始出现滚珠不受载现象,继续增大时,螺母B 中所有滚珠与滚道完全脱开,形成卸载状态,造成滚珠丝杠副的失效.(2)轴向外载荷一定时,倾覆力矩会导致双螺母滚珠丝杠副的载荷分布迅速变差,即载荷分布曲线的波动幅度变大.如本文使用的4010型滚珠丝杠副,当倾覆力矩从10k N mm 增加到30k N mm 时,螺母A 和螺母B 的载荷波动幅度分别增大60.37%和128.64%.因此在实际应用中,应尽量避免倾覆力矩的存在,否则会由于滚珠受力不均导致滚珠丝杠副的刚性降低,寿命缩短.(3)轴向外载荷㊁倾覆力矩一定时,滚珠的尺寸误差和滚道的齿形误差会使滚珠与滚道之间的法向接触载荷沿着无误差时的载荷分布曲线上下波动,且误差范围越大,波动幅值越大,载荷分布越不均匀;丝杠的导程误差会使螺母A 的受载增大,螺母B 的受载减小.在误差大小一定的情况下,导程误差对载荷分布的影响程度大于尺寸误差和齿形误差,即双螺母滚珠丝杠副的载荷分布对导程误差的敏感程度更高.(4)在轴向外载荷㊁几何误差和倾覆力矩的共同作用下,几何误差对滚珠载荷分布的影响较大,会抵消部分倾覆力矩带来的影响.滚珠尺寸误差增大时,螺母B 中部分滚珠受到的法向接触载荷会显著增大或减小,在重载情况下更容易出现第一颗滚珠不受载㊁与滚道脱离的现象,但也可减缓螺母B 中所有滚珠与滚道脱离,即卸载状态的发生.参考文献:[1]㊀OH KJ ,C A O L ,C HU N GSC .E x pl i c i tM o d e l Gi n g a n d I n v e s t i g a t i o no f F r i c t i o nT o r qu e s i nD o u b l e Gn u tB a l lS c r e w sf o rt h e P r e c i s i o n D e s i gn o f B a l l S c r e w F e e d D r i v e s [J ].T r i b o l o g y In t e r n a t i o n a l ,2019,141:105841.9811 几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响席静谣㊀周长光㊀冯虎田等。
单选题随着液压技术、(传感器技术)、精密机械装置技术、自动控制技术、微型计算机技术和人工智能技术等新技术的发展并不断地采用,机电一体化技术正向着自动化和智能化方向发展。
2、常用的机电一体化设计方法有机电互补法、(融合法)和组合法3 种。
(信息处理)技术包括信息的交换、存取、运算、判断和决策,主要设备是计算机或可编程序控制器等。
机电一体化系统中,(电子信息处理子系统)是指系统中将来自传感器的检测信息和外部输入命令进行集中、存储、分析、加工,根据信息处理结果,按照一定的程序和节奏发出相应的指令,控制整个系统按序、有目的地运行。
(系统)技术是以整体的概念组织应用各种相关技术,从系统目标出发,将整体分解成相关的若干子系统。
(自动控制)技术主要包括基本控制理论、自动控制设计及计算机系统仿真及研制等。
7、谐波齿轮减速器主要由钢轮、柔轮和(谐波发生器)构建组成。
8、啮合传动装置可分为齿轮传动装置和(蜗杆传动装置)。
9、导轨副中的运动件沿支承导件运动,其运动方向有直线运动和(回转运动)两种。
10、滚珠丝杆的支撑常采用以(推力轴承)为主的轴承组合11、滚珠丝杆副是一种(螺旋传动装置)。
12、系统刚度越大,动力损失越小,增加了(闭环伺服系统)的稳定性。
13 、标准滚动轴承在使用时,主要根据刚度和(转速)来选择。
轴的(回转精度)是指在运转过程中轴的瞬间回转中心线的变动情况。
15、动力装置的作用是将电能或液(气)压能转换为(机械能)。
16、步进电动机可按照输入的脉冲指令一步步地旋转,即可将输入的数字信号转换成相应的(角位移)。
17、热变形式微动装置利用(电热元件)作为动力源,靠其通电后产生的热变形实现微小位移。
18、(主轴部件)在机电一体化系统中,是直接影响生产效率的执行装置。
19、空心截面惯性矩的比实心的大,加大截面轮廓尺寸,(减小)壁厚,也可以大大提高刚度。
20、对轴承有特殊要求而又不可能采用标准滚动轴承时,就需要根据使用要求自行设计(非标准滚动轴承)。
超磁致伸缩滚珠丝杠副智能预紧技术
在工程领域中,超磁致伸缩滚珠丝杠副智能预紧技术是一项备受关注
的前沿研究课题。
本文将深入探讨这一技术的原理、应用及未来发展
趋势,希望能够为您对该主题的深入理解提供有益帮助。
1. 技术原理
超磁致伸缩滚珠丝杠副智能预紧技术是基于磁致伸缩材料的特性,通
过控制磁场来实现对滚珠丝杠副的智能预紧。
磁致伸缩材料的磁化强
度可以受到外界磁场的影响而发生变化,利用这一特性可以实现对滚
珠丝杠副的精准控制和调节,从而提高其工作效率和稳定性。
2. 技术应用
超磁致伸缩滚珠丝杠副智能预紧技术在工程机械领域具有广泛的应用
前景。
在数控机床、机器人臂、航空航天设备等领域,利用该技术可
以实现对传动系统的高精度控制和长期稳定运行,提高设备的工作效
率和可靠性。
3. 技术发展趋势
随着工业自动化和智能化水平的不断提高,超磁致伸缩滚珠丝杠副智
能预紧技术将在未来得到更广泛的应用。
随着磁致伸缩材料和控制技
术的不断创新,该技术将不断提升在精密制造和高端装备领域的地位,为工程技术的发展带来新的机遇和挑战。
总结回顾
通过本文的介绍,相信您对超磁致伸缩滚珠丝杠副智能预紧技术已经
有了一定的了解。
在未来的工作和研究中,我们应该密切关注该技术
的最新进展,不断深化对其原理和应用的理解,以推动相关领域的技
术创新和发展。
个人观点与理解
作为一项新兴的前沿技术,超磁致伸缩滚珠丝杠副智能预紧技术在工
程领域具有重要意义。
我个人认为,通过深入研究和实践,可以进一
步发挥该技术的优势,为工程制造和设备运行提供更加可靠和高效的
解决方案。
结语
以上是对超磁致伸缩滚珠丝杠副智能预紧技术的介绍与探讨,希望能
为您对该主题的深入理解提供帮助。
在未来的工作和学习中,让我们
共同关注该技术的发展动态,为工程技术的进步贡献自己的一份力量。
结尾。
超磁致伸缩滚珠丝杠副智能预紧技术是一种能够实现滚珠丝杠
副智能预紧的技术,它利用磁致伸缩材料的特性,通过控制磁场来实
现对滚珠丝杠副的精准控制和调节,从而提高其工作效率和稳定性。
这项技术在工程领域中有着广泛的应用前景,特别是在工业自动化和
智能化水平不断提高的今天,其重要性更加突出。
超磁致伸缩材料是一种特殊的功能材料,其在外加磁场的作用下能够
发生磁致伸缩效应,即在磁场作用下产生形变。
利用这一特性,可以
实现对滚珠丝杠副的智能预紧。
通过控制磁场的强度和方向,可以准
确地控制滚珠丝杠副的预紧力,从而保证其在工作过程中的稳定性和
精准性。
在工程机械领域中,超磁致伸缩滚珠丝杠副智能预紧技术有着广泛的
应用。
在数控机床、机器人臂、航空航天设备等领域,利用该技术可
以实现对传动系统的高精度控制和长期稳定运行,提高设备的工作效
率和可靠性。
而且,在一些需要高精度控制和稳定性的领域,如光学
仪器制造、半导体设备制造等,这项技术也具有重要的应用价值。
随着工业自动化和智能化水平的不断提高,超磁致伸缩滚珠丝杠副智
能预紧技术将在未来得到更广泛的应用。
随着磁致伸缩材料和控制技
术的不断创新,该技术将不断提升在精密制造和高端装备领域的地位,为工程技术的发展带来新的机遇和挑战。
近年来,随着人工智能、大数据、云计算等新兴技术的快速发展,工
业智能化已经成为国家制造业转型升级的重要方向。
超磁致伸缩滚珠
丝杠副智能预紧技术作为工程智能制造的重要支撑技术之一,将会在
智能制造领域发挥重要作用。
它不仅能够提高设备的工作效率和稳定性,还能够为工程制造领域的高精度加工和自动化生产提供技术支持。
在未来的工作和研究中,需要重点关注超磁致伸缩滚珠丝杠副智能预紧技术的关键技术问题,包括磁致伸缩材料的改性和性能优化、磁场控制技术的精度和稳定性提升、智能预紧算法的改进与优化等方面。
需要加强跨学科、跨行业的合作交流,推动超磁致伸缩滚珠丝杠副智能预紧技术的理论研究和工程应用,为智能制造和工程技术的发展做出贡献。
超磁致伸缩滚珠丝杠副智能预紧技术是一项具有重要应用价值和发展前景的前沿技术,在工程制造领域有着广阔的应用前景。
随着技术的不断创新和突破,相信这项技术将为工程技术的发展和智能制造的进步带来新的机遇和挑战。
希望通过我们的共同努力,能够推动超磁致伸缩滚珠丝杠副智能预紧技术走向成熟和应用,为工程领域的发展做出更大的贡献。