河北省清河挥公实验中学2020届高考数学一轮复习 面面平行学案(无答案)

一、
因为多面体的各个面都是平面，所以多面体的侧面积就是侧面展开图的面积，旋转体的侧面积和表面积
，则
侧＝
某几何体的三视图如图所示，该几何体的表面积是
某几何体的三视图如图所示，则其表面积为________．
三、考点归纳
考向一：三视图与几何体的表面积
例1 (1)[2014·浙江高考]某几何体的三视图(单位：cm)如图所示，则该几何体的表面积是( )
A. 90 cm2
B. 129 cm
(2)[2013·重庆高考]某几何体的三视图如图所示，
重点展示群学问题及难点问题，暴露学生学习问题，形成学习成果、总结规律和
A. 48＋12 2
B. 48＋242
C. 3612 2
D. 36＋24 2
、(2012·北京)某三棱锥的三视图如图所示，该三棱锥的表面积是（
．28＋6 5 B．30＋65C．58 5 D．60＋12 5
正四棱锥的顶点都在同一球面上．若该棱锥的高为。

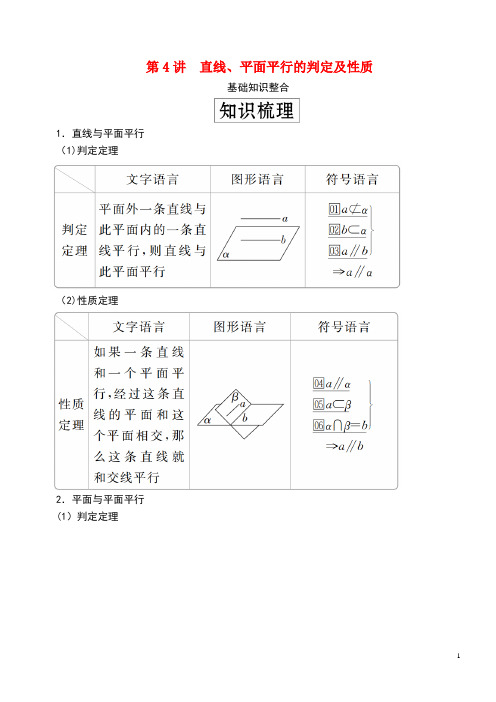
第4讲直线、平面平行的判定及性质基础知识整合1．直线与平面平行（1)判定定理（2)性质定理2．平面与平面平行(1）判定定理（2）性质定理1．垂直于同一条直线的两个平面平行,即若a⊥α，a⊥β，则α∥β.2．垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥b.3．平行于同一个平面的两个平面平行,即若α∥β,β∥γ，则α∥γ.1．已知直线l和平面α,若l∥α，P∈α，则过点P且平行于l的直线( ) A．只有一条,不在平面α内B．只有一条，且在平面α内C．有无数条，一定在平面α内D．有无数条，不一定在平面α内答案B解析过直线外一点作该直线的平行线有且只有一条，因为点P在平面α内，所以这条直线也应该在平面α内．2．（2019·吉林普通中学模拟)已知α，β表示两个不同的平面，直线m是α内一条直线，则“α∥β "是“m∥β”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案A解析由α∥β,m⊂α，可得m∥β；反过来，由m∥β，m⊂α,不能推出α∥β。

综上，“α∥β”是“m∥β”的充分不必要条件．3．若空间四边形ABCD的两条对角线AC,BD的长分别是8,12，过AB的中点E且平行于BD，AC的截面四边形的周长为（）A．10 B．20C．8 D．4答案B解析设截面四边形为EFGH，F,G，H分别是BC，CD，DA的中点，∴EF＝GH＝4，FG＝HE ＝6.∴周长为2×(4＋6)＝20.4．如图所示，P为矩形ABCD所在平面外一点，矩形对角线交点为O,M为PB的中点，给出下列五个结论：①PD∥平面AMC；②OM∥平面PCD；③OM∥平面PDA；④OM∥平面PBA；⑤OM∥平面PBC。

其中正确的个数是( ）A．1 B．2C．3 D．4答案C解析矩形ABCD的对角线AC与BD交于点O,所以O为BD的中点．在△PBD中,M是PB的中点，所以OM是△PBD的中位线，OM∥PD，则PD∥平面AMC，OM∥平面PCD，且OM∥平面PDA.因为M∈PB,所以OM与平面PBA，平面PBC相交．5．(2019·南通模拟)如图,四棱锥P－ABCD的底面是一直角梯形，AB∥CD，BA⊥AD，CD＝2AB，PA⊥底面ABCD，E为PC的中点，则BE与平面PAD的位置关系为________．答案平行解析取PD的中点F，连接EF，AF，在△PCD中，EF綊错误!CD。

2019-2020学年高考数学一轮复习 7.4直线、平面平行的判定与性质学案学考考查重点 1.考查空间平行关系的判定及性质有关命题的判定；2.解答题中证明或探索空间的平行关系．本节复习目标 1.熟练掌握线面平行、面面平行的判定定理和性质，会把空间问题转化为平面问题，解答过程的叙述步骤要完整，避免因条件书写不全而失分；2.学会应用“化归思想”进行“线线问题、线面问题、面面问题”的互相转化，牢记解决问题的根源在“定理”．教材链接·自主学习1．直线与平面平行的判定与性质判定性质定义定理图形条件a∩α＝∅a⊂α，b⊄α，a∥b a∥αa∥α，a⊂β，α∩β＝b结论a∥αb∥αa∩α＝∅a∥b 2. 面面平行的判定与性质判定性质定义定理图形条件α∩β＝∅a⊂β，b⊂β，a∩b＝P，a∥α，b∥αα∥β，α∩γ＝a，β∩γ＝bα∥β，a⊂β结论α∥βα∥βa∥b a∥α基础知识·自我测试1．已知不重合的直线a，b和平面α，①若a∥α，b⊂α，则a∥b；②若a∥α，b∥α，则a∥b；③若a∥b，b⊂α，则a∥α；④若a∥b，a∥α，则b∥α或b⊂α.上面命题中正确的是________(填序号)．2．已知α、β是不同的两个平面，直线a⊂α，直线b⊂β，命题p：a与b没有公共点；命题q：α∥β，则p是q的____________条件．3．已知平面α∥平面β，直线a⊂α，有下列命题：①a与β内的所有直线平行；②a与β内无数条直线平行；③a与β内的任意一条直线都不垂直．其中真命题的序号是________．4．(2013·浙江)若直线l不平行于平面α，且l⊄α，则( )A．α内的所有直线与l异面 B．α内不存在与l平行的直线C．α内存在唯一的直线与l平行 D．α内的直线与l都相交5．(2012·四川)下列命题正确的是( )A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行题型分类·深度剖析题型一直线与平面平行的判定与性质例1正方形ABCD与正方形ABEF所在平面相交于AB，在AE、BD上各有一点P、Q，且AP ＝DQ.求证：PQ∥平面BCE.变式训练1：如图，在四棱锥P—ABCD中，底面ABCD是菱形，∠BAD＝60°，AB＝2，PA＝1，PA⊥平面ABCD，E是PC的中点，F是AB的中点．求证：BE∥平面PDF.题型二平面与平面平行的判定与性质例2如图，在三棱柱ABC—A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EFA1∥平面BCHG.变式训练2：证明：若一条直线与两个相交平面都平行，则这条直线平行于两个平面的交线．题型三平行关系的综合应用例3如图所示，在四面体ABCD中，截面EFGH平行于对棱AB和CD，试问截面在什么位置时其截面面积最大？变式训练3：如图，在正方体ABCD—A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO?。

第39讲直线、平面平行的判定及其性质课时达标一、选择题1．已知两个不同的平面α，β，两条不同的直线a，b,a⊂α，b⊂α，则“a∥β，b∥β”是“α∥β”的（)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件B解析因为“a∥β，b∥β”，若a∥b，则α与β不一定平行，反之若“α∥β”，则一定有“a∥β，b∥β”．故选B.2．如图,在空间四边形ABCD中，E，F分别为边AB，AD上的点，且AE∶EB＝AF∶FD＝1∶4，又H，G分别为BC，CD的中点，则（)A．BD∥平面EFGH，且四边形EFGH是矩形B．EF∥平面BCD，且四边形EFGH是梯形C．HG∥平面ABD，且四边形EFGH是菱形D．EH∥平面ADC,且四边形EFGH是平行四边形B解析由AE∶EB＝AF∶FD＝1∶4知EF綊15BD,所以EF∥平面BCD.又H，G分别为BC，CD的中点，所以HG綊错误!BD，所以EF∥HG且EF≠HG，所以四边形EFGH是梯形．3．能使直线a与平面α平行的条件是（）A．直线与平面内的一条直线平行B．直线与平面内的某条直线不相交C．直线与平面内的无数条直线平行D．直线与平面内的所有直线不相交D解析A项不正确，由直线与平面内的一条直线平行，不能推出直线与平面平行，直线有可能在平面内;B项不正确，由直线与平面内的某条直线不相交,不能推出直线与平面平行，直线有可能在平面内,也可能和平面相交；C项不正确，由直线与平面内的无数条直线平行，不能推出直线与平面平行，直线有可能在平面内；D项正确，由直线与平面内的所有直线不相交,依据直线和平面平行的定义可得直线与平面平行．4．（2019·山东师大附中月考）如图，在长方体ABCD－A′B′C′D′中，下列直线与平面AD′C平行的是（)A．B′C′ B．A′BC．A′B′ D．BB′B解析连接A′B，因为A′B∥CD′，CD′⊂平面AD′C，所以A′B∥平面AD′C.5．已知a，b表示不同的直线,α，β表示不同的平面,则下列命题正确的是( )A．若a∥α，b∥β,α∥β，则a∥bB．若a∥b，a⊂α,b⊂β,则α∥βC．若a∥b，α∩β＝a，则b∥α或b∥βD．若直线a与b异面，a⊂α，b⊂β，则α∥βC解析对于A项,a与b还可能相交或异面，此时a与b不平行，故A项不正确；对于B 项，α与β可能相交，此时设α∩β＝m,则a∥m，b∥m，则a∥b，故B项不正确；对于D 项，α与β可能相交,如图所示，故D项不正确．故选C。

8.3 直线、平面平行的判定与性质『考纲要求』1．考查空间直线与平面平行，面面平行的判定及其性质．2．以解答题的形式考查线面的平行关系．3．考查空间中平行关系的探索性问题．『教学目标』1．熟练掌握线面平行、面面平行的判定定理和性质，会把空间问题转化为平面问题，解答过程中叙述的步骤要完整，避免因条件书写不全而失分．2．学会应用“化归思想”进行“线线问题、线面问题、面面问题”的互相转化，牢记解决问题的根源在“定理”．『基础梳理』1．平面与平面的位置关系有相交、平行两种情况．2．直线和平面平行的判定(1)定义：直线和平面没有公共点，则称直线平行于平面；(2)判定定理：a⊄α，b⊂α，且a∥b⇒a∥α；(3)其他判定方法：α∥β；a⊂α⇒a∥β.3．直线和平面平行的性质定理：a∥α，a⊂β，α∩β＝l⇒a∥l.4．两个平面平行的判定(1)定义：两个平面没有公共点，称这两个平面平行；(2)判定定理：a⊂α，b⊂α，a∩b＝M，a∥β，b∥β⇒α∥β；(3)推论：a∩b＝M，a，b⊂α，a′∩b′＝M′，a′，b′⊂β，a∥a′，b∥b′⇒α∥β.5．两个平面平行的性质定理(1)α∥β，a⊂α⇒a∥β；(2)α∥β，γ∩α＝a，γ∩β＝b⇒a∥b.6．与垂直相关的平行的判定(1)a⊥α，b⊥α⇒a∥b；(2)a⊥α，a⊥β⇒α∥β.7.一个关系平行问题的转化关系：8.两个防范(1)在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误．(2)把线面平行转化为线线平行时，必须说清经过已知直线的平面与已知平面相交，则直线与交线平行．『考向探究』考向一直线与平面平行的判定与性质『例1』如图，在四棱锥P ABCD中，底面ABCD为平行四边形，O为AC的中点，M为PD的中点．求证：PB∥平面ACM.『训练1』如图，若P A⊥平面ABCD，四边形ABCD是矩形，E、F分别是AB、PD的中点，求证：AF∥平面PCE.考向二平面与平面平行的判定与性质『例2』如图，在正方体ABCDA1B1C1D1中，M、N、P分别为所在边的中点．求证：平面MNP∥平面A1C1B；『训练2』如图，在三棱柱ABC-A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EF A1∥平面BCHG.考向三线面平行中的探索问题『例3』如图所示，在三棱柱ABC-A1B1C1中，A1A⊥平面ABC，若D是棱CC1的中点，问在棱AB上是否存在一点E，使DE∥平面AB1C1？若存在，请确定点E的位置；若不存在，请说明理由．『训练3』如图，在四棱锥P-ABCD中，底面是平行四边形，P A⊥平面ABCD，点M、N分别为BC、P A的中点．在线段PD上是否存在一点E，使NM∥平面ACE？若存在，请确定点E的位置；若不存在，请说明理由．怎样证明线线、线面、面面平行与垂直的综合性问题『问题研究』 高考对平行、垂直关系的考查主要以线面平行、线面垂直为核心，以多面体为载体结合平面几何知识，考查判定定理、性质定理等内容，难度为中低档题目.『解决方案』 利用定理证明线面关系时要注意结合几何体的结构特征，尤其注意对正棱柱、正棱锥等特殊几何体性质的灵活运用，进行空间线面关系的相互转化. 『示例』如图，在四棱台ABCD -A 1B 1C 1D 1中，D 1D ⊥平面ABCD ，底面ABCD 是平行四边形，AB ＝2AD ，AD ＝A 1B 1，∠BAD ＝60°. (1)证明：AA 1⊥BD ； (2)证明：CC 1∥平面A 1BD .第(1)问转化为证明BD 垂直A 1A 所在平面；第(2)问在平面A 1BD 内寻找一条线与CC 1平行．『解答示范』 证明 (1)因为D 1D ⊥平面ABCD ，且BD ⊂平面ABCD ， 所以D 1D ⊥BD .(1分)又因为AB ＝2AD ，∠BAD ＝60°，在△ABD 中，由余弦定理得BD 2＝AD 2＋AB 2－2AD ·AB cos 60°＝3AD 2，所以AD 2＋BD 2＝AB 2， 因此AD ⊥BD .(4分) 又AD ∩D 1D ＝D ， 所以BD ⊥平面ADD 1A 1. 又AA 1⊂平面ADD 1A 1， 故AA 1⊥BD .(6分)(2)如图，连结AC ，A 1C 1， 设AC ∩BD ＝E ，连结EA 1， 因为四边形ABCD 为平行四边形， 所以EC ＝12AC .(8分)由棱台定义及AB ＝2AD ＝2A 1B 1知A 1C 1∥EC 且A 1C 1＝EC ，所以四边形A 1ECC 1为平行四边形，(10分) 因此CC 1∥EA 1.又因为EA1⊂平面A1BD，CC1⊄平面A1BD，所以CC1∥平面A1BD.(12分)证明线面关系不能仅仅考虑线面关系的判定和性质，更要注意对几何体的几何特征的灵活应用．证明的依据是空间线面关系的判定定理和性质定理．另外根据几何体的数据，通过计算也可得到线线垂直的关系，所以要注意对几何体中的数据的正确利用．『试一试』如图，在多面体ABCDEF中，四边形ABCD是正方形，AB＝2EF＝2，EF∥AB，EF⊥FB，∠BFC＝90°，BF＝FC，H为BC的中点．(1)求证：FH∥平面EDB；(2)求证：AC⊥平面EDB；(3)求四面体BDEF的体积．答案『例1』『审题视点』 连接MO ，证明PB ∥MO 即可．证明 连接BD ，MO .在平行四边形ABCD 中，因为O 为AC 的中点，所以O 为BD 的中点．又M 为PD 的中点，所以PB ∥MO .因为PB ⊄平面ACM ，MO ⊂平面ACM ，所以PB ∥平面ACM .利用判定定理时关键是找平面内与已知直线平行的直线．可先直观判断平面内是否已有，若没有，则需作出该直线，常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线． 『训练1』证明 取PC 的中点M ，连接ME 、MF ， 则FM ∥CD 且FM ＝12CD .又∵AE ∥CD 且AE ＝12CD ，∴FM AE ，即四边形AFME 是平行四边形． ∴AF ∥ME ，又∵AF ⊄平面PCE ，EM ⊂平面PCE ， ∴AF ∥平面PCE . 『例2』『审题视点』 证明MN ∥A 1B ， MP ∥C 1B .证明 连接D 1C ，则MN 为△DD 1C 的中位线， ∴MN ∥D 1C .又∵D 1C ∥A 1B ，∴MN ∥A 1B .同理，MP ∥C 1B .而MN 与MP 相交，MN ，MP 在平面MNP 内，A 1B ，C 1B 在平面A 1C 1B 内．∴平面MNP ∥平面A 1C 1B .证明面面平行的方法有：(1)面面平行的定义；(2)面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行；(3)利用垂直于同一条直线的两个平面平行；(4)两个平面同时平行于第三个平面，那么这两个平面平行；(5)利用“线线平行”、“线面平行”、“面面平行”的相互转化．『训练2』证明(1)∵GH是△A1B1C1的中位线，∴GH∥B1C1.又∵B1C1∥BC，∴GH∥BC，∴B，C，H，G四点共面．(2)∵E、F分别为AB、AC的中点，∴EF∥BC，∵EF⊄平面BCHG，BC⊂平面BCHG，∴EF∥平面BCHG.∵A1G EB，∴四边形A1EBG是平行四边形，∴A1E∥GB.∵A1E⊄平面BCHG，GB⊂平面BCHG.∴A1E∥平面BCHG.∵A1E∩EF＝E，∴平面EF A1∥平面BCHG.『例3』『审题视点』取AB、BB1的中点分别为E、F，证明平面DEF∥平面AB1C1即可．解存在点E，且E为AB的中点．下面给出证明：如图，取BB1的中点F，连接DF，则DF∥B1C1.∵AB的中点为E，连接EF，则EF∥AB1.B1C1与AB1是相交直线，∴平面DEF∥平面AB1C1.而DE⊂平面DEF，∴DE∥平面AB1C1.解决探究性问题一般要采用执果索因的方法，假设求解的结果存在，从这个结果出发，寻找使这个结论成立的充分条件，如果找到了符合题目结果要求的条件，则存在；如果找不到符合题目结果要求的条件(出现矛盾)，则不存在．『训练3』解在PD上存在一点E，使得NM∥平面ACE.证明如下：如图，取PD的中点E，连接NE，EC，AE，因为N，E分别为P A，PD的中点，所以NE 12AD.又在平行四边形ABCD中，CM 12AD.所以NE MC，即四边形MCEN是平行四边形．所以NM EC.又EC⊂平面ACE，NM⊄平面ACE，所以MN∥平面ACE，即在PD上存在一点E，使得NM∥平面ACE.『试一试』『尝试解答』(1)证明设AC与BD交于点G，则G为AC的中点．连EG，GH，由于H为BC的中点，故GH 12AB.又EF 12AB，∴EF GH.∴四边形EFHG为平行四边形．∴EG∥FH，而EG⊂平面EDB，∴FH∥平面EDB. (2)证明由四边形ABCD为正方形，有AB⊥BC.又EF∥AB，∴EF⊥BC.而EF⊥FB，∴EF⊥平面BFC，∴EF⊥FH.∴AB⊥FH.又BF＝FC，H为BC的中点，∴FH⊥BC.∴FH⊥平面ABCD.∴FH⊥AC.又FH∥EG，∴AC⊥EG.又AC⊥BD，EG∩BD＝G，∴AC⊥平面EDB.(3)解∵EF⊥FB，∠BFC＝90°，∴BF⊥平面CDEF.∴BF为四面体BDEF的高．又BC＝AB＝2，∴BF＝FC＝ 2.V B－DEF＝13×12×1×2×2＝13.。

芯衣州星海市涌泉学校§线面平行与面面平行【复习目的】1． 掌握直线与平面、平面与平面平行的定义、断定定理和性质定理，并能运用这些知识进展论证或者者解题； 2． 理解线线平行、线面平行、面面平行之间的转化以及平行与垂直之间的转化的辩证关系。

【课前预习】1. 空间平面与平面的位置关系分类、三个平行关系的转化：2. 假设直线a ⊥平面α，直线b α，直线a 与b 的位置关系是〔〕A ．a bB ．a b ⊥C ．,a b 一定异面D ．,a b 一定相交3. 假设直线l 平面α，那么以下命题中正确的选项是〔〕A ．l 平行于α内所有直线B ．l 平行于过l 的平面与α的交线C ．l 平行于α内的任一直线D ．l 平行于α内唯一确定的直线4. 两条异面直线a 、b 分别在平面α、β内，且βα =c ，那么直线c 〔〕A ．一定与a,b 都相交B ．至少与a,b 中的一条相交C ．至多与a,b 中的一条相交D ．一定与a,b 都不相交5. 直线,a b 和平面α，那么a b 的一个必要不充分条件是〔〕A ．,a b ααB ．,a b αα⊥⊥C ．,b a αα⊂D ．,a b 与α成等角6. ,αβ表示两个平面，,a b 表示两条直线，那么a α的一个充分条件是〔〕A ．,a αββ⊥⊥B ．,b a b αβ=C ．,a b b αD ．,a αββ⊂7. 判断真假：〔1〕平行于同一直线的两直线平行〔〕；〔2〕平行于同一直线的两平面平行〔〕；〔3〕平行于同B 1Q一平面的两直线平行〔〕；〔4〕平行于同一平面的两平面平行〔〕；〔5〕垂直于同一平面的两直线平行〔〕；〔6〕垂直于同一平面的两平面平行〔〕；〔7〕垂直于同一直线的两直线平行〔〕；〔8〕垂直于同一直线的两平面平行〔〕；〔9〕一个平面上不一一共线的三点到另一个平面间隔相等，那么这两个平面平行〔〕；〔10〕与同一条直线成等角的两个平面平行〔〕。

2.2.3-2．2.4线面平行与面面平行的性质导学案【学习目标】1. 掌握直线与平面平行的性质定理2. 平面与平面平行的性质定理3. 熟练掌握两个性质定理的应用 【自主探究】1.一条直线与平面平行，并不能保证这个平面内的所有直线都与这个直线平行2.直线a 与平面α平行，如何在平面α内找到与直线a 平行的直线？3. 直线与平面平行性质定理：简记为 线面平行则线线平行4.若两个平面平行，那一个平面内的直线与另一个平面内的直线具有怎样位置关系？5. 平面与平面平行性质定理：简记为 面面平行则线线平行6.其它性质：①//,//l l αβαβ⊂⇒；即：面面平行则线面平行②//αβ，//βγ，则//αγ．③夹在平行平面间的平行线段相等.7.总结线线平行、线面平行、面面平行之间的条件和结论，能发现它们内在的联系吗？【课堂精讲】例1.判断下列命题是否正确（1）如果a ，b 是两条直线，且a//b ，那么a 平行于经过b 的任何平面。

（2）如果直线a 和平面α满足a//α，那么a 与α内的任何直线平行。

（3）如果直线a ，b 和平面α，满足a//α, b //α，那么a//b 。

（4）如果直线a ，b 和平面α，满足a//b, a//α,b ⊄α，则b//α 。

（5）过直线外一点，有且仅有一个平面和已知直线平行。

（6）如果直线l 和平面α平行，那么过平面α内一点和直线l 平行的直线在α内。

例2．已知四边形ABCD 是空间四边形，E 、F 、G 、H 、分别是边AB 、BC 、CD 、DA 的中点。

（1）求证：四边形EFGH 是平行四边形。

（2）求证：直线BD//平面EFGH例3.如图四面体ABCD 被平面所截，截面与四条棱AD ，AB ，CB ，CD 相交与点E ，F ，G ，H 四点，且截面EFGH 是平行四边形，求证：AC//平面EFGH 。

例4.如图，空间四边形ABCD 的对棱AD 、BC 成600的角，且AD BC a ==，平行于AD 与BC的截面分别交AB 、AC 、CD 、BD 于E 、F 、G 、H ． (1)求证：四边形EGFH 为平行四边形；(2)E 在AB 的何处时截面EGFH1. 课堂小结：2.本节课学习内容中的问题和疑难D。

§2.2.2 平面与平面平行的判定一、学习目标1、识记两平面平行的判定定理并会应用证明简单的几何问题。

2、让学生通过观察实物及模型，得出两平面平行的判定。

3、进一步培养学生空间问题平面化的思想。

二、考纲要求：两个平面平行的判定定理及应用。

三、学习指导：认真阅读课本56、57页，并提出问题。

四、自主学习（一）创设情景、引入课题引导学生观察、思考教材第57页的观察题，导入本节课所学主题。

（二）研探新知上节课我们研究了直线与平面平行的判断依据，具有什么条件的两个平面是平行的呢?1、问题：（1）平面β内有一条直线与平面α平行，α、β平行吗？（2）平面β内有两条直线与平面α平行，α、β平行吗？（3）平面α内有无数条直线与平面β平行，则α∥β，对吗?（4）如下图，平面β内有两条相交直线与平面α平行，情况如何？通过长方体模型，引导学生观察、思考、交流，得出结论。

两个平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

（1）简记为：线面平行，则面面平行（2）符号表示：a βb βa∩b = P β∥αa∥αb∥α（3）定理说明作用：判定或证明面面平行。

关键：一个平面内的两条相交直线与另一个平面平。

思想：空间问题化为平面问题。

五、典型例题例1 已知正方体ABCD-1111A B C D ,求证：平面11AB D //平面1C BD 。

例2 如图，在正方体1111ABCD A B C D 中，求证：平面1A BD //平面11CD B ．变式练习：58页练习第2题。

六、小结1、判断证明两平面平行的方法有三种： （1）用定义；两个平面没有公共点。

（2）判定定理；线面平行---面面平行 （3）垂直于同一条直线的两个平面平行。

2、数学思想方法：转化思想----空间问题平面化 七、学习评价1D1A1C 1BABDC1、直线 a ∥平面α，平面α内有 n 条互相平行的直线，那么这 n 条直线和直线 a( )（A ）全平行 （B ）全异面 （C ）全平行或全异面 （D ）不全平行也不全异面2、直线 a ∥平面α，平面α内有无数条直线 交于 一点，那么这无数条直线中与直线 a 平行的 （ ） （A ）至少有一条 （B ）至多有一条 （C ）有且只有一条 （D ）不可能有3、判断下列命题是否正确（1）若平面α内的两条直线分别与平面β平行，则平面α与平面β平行； （2）若平面α内有无数条直线分别与平面β平行，则平面α与平面β平行； （3）平行于同一直线的两个平面平行；（4）两个平面分别经过两条平行直线，这两个平面平行；（5）过已知平面外一条直线，必能作出与已知平面平行的平面．4、若a ，b 为异面直线βα⊂⊂b a ,，则α与β的位置关系_____________. 八、课后作业1．设直线l 、 m, 平面α、β,下列条件能得出α∥β的有 ( )①l ⊂α,m ⊂α,且l ∥β,m ∥β；②l ⊂α,m ⊂α,且l ∥m ；③l ∥α,m ∥β,且l ∥m A ． 1个 B. 2个 C. 3个 D. 0个 2．下列命题中为真命题的是（ ）A. 平行于同一条直线的两个平面平行B. 垂直于同一条直线的两个平面平行C. 若—个平面内至少有三个不共线的点到另—个平面的距离相等，则这两个平面平行．D.若三条直线a 、b 、c 两两平行，则过直线a 的平面中，有且只有—个平面与b ，c 都平行．3．下列命题中正确的是( )①平行于同一直线的两个平面平行； ②平行于同一平面的两个平面平行； ③垂直于同一直线的两个平面平行； ④与同一直线成等角的两个平面平行 A. ①② B. ②③ C. ③④ D ②③④ 4． 下列命题中正确的是 （填序号）；①一个平面内两条直线都平行于另一个平面，那么这两个平面平行；②如果一个平面内任何一条直线都平行于另一个平面，那么这两个平面平行； ③平行于同一直线的两个平面一定相互平行；④如果一个平面内的无数条直线都平行于另一个平面，那么这两个平面平行 ； 5． 若夹在两个平面间的三条平行线段相等，那么这两个平面的位置关系是 ；6. 如图，直线AA '，BB '，CC '相交于O ，AO AO ='，BO BO ='，CO C O ='． 求证：平面ABC //平面ABC '''．O ABCA 'B 'C '7、习题2.2（A组）第7题九、反思总结。