【全国百强校】江苏省无锡市第一中学2017-2018学年高一下学期期末考试数学试题(解析版)

江苏省无锡市普通高中2017-2018学年高一下学期期末考试物理试题一、单项选择题1. 在光滑绝缘的水平地面上有两个带同种电荷的小球,将两个小球由静止释放后,两小球之间的库仑力将（）A. 不变B. 变小C. 变大D. 无法确定2. 关于开普勒对行星运动规律的认识,下列说法中正确的是（）A. 所有行星绕太阳的运动都是匀速圆周运动B. 所有行星以相同的速率绕太阳做椭圆运动C. 所有行星轨道的半长轴的二次方与公转周期的三次方的比值都相同D. 对于每一个行星,它在近日点时的速率均大于在远日点的速率3. 在下面各实例中，机械能守恒的是（）A. 树上飘落的树叶B. 在空中匀速下降的跳伞运动员C. 在空中做平抛运动的铅球D. 草坪上滚动的足球4. 一端固定的轻质弹簧处于原长,现用互相垂直的两个力拉弹簧的另一端至点,如图所示,在此过程分别做了的功;换用另一个力仍使弹簣重复上述过程,则该过程中所做的功是（）......A. B. C. D.5. 若在地面上沿水平方向直接发射一飞行器,如果发射速度大于,小于,(不计空气阻力)则它将（）A. 围绕地球做圆周运动B. 围绕地球做椭圆运动C. 挣脱地球的束缚绕太阳运动D. 挣脱太阳的束缚飞离太阳系6. 用控制变量法,可以研究影响平行板电容器电容的因素(如图).设两极板正对面积为,极板间的距离为,静电计指针偏角为.实验中,极板所带电荷量不变,若（）A. 保持不变,增大,则变大B. 保持不变,增大,则变小C. 保持不变,减小,则变小D. 保持不变,减小,由不变7. 将一电荷量为的小球放在不带电的金属球附近,所形成的电场线分布如图所示,金属球表面的电势处处相等. 为电场中的两点,则（）A. 点的电场强度比点的小B. 点的电势比点的低C. 将检验电荷从点移到点的过程中,电场力做正功D. 检验电荷在点的电势能比在点的小8. 如图所示,质量为和的小球和,系在长为的光滑细线两端桌面水平光滑,高,球无初速度从桌边滑下,落在沙地上静止不动,则球离开桌边的速度为（）A. B. C. D.二、多项选择题9. 关于同步卫星下列说法正确的是（）A. 同步卫星的质量一定相同B. 同步卫星不可能通过无锡的正上空C. 运行周期有可能小于D. 同步卫星距离地面高度一定相同10. 如图所示是北斗导航系统中部分卫星的轨道示意图,已知三颗卫星均做匀速圆周运动,其中是地球同步卫星,则（）A. 卫星的角速度小于卫星的角速度B. 卫星的线速度大小等于卫星的线速度大小C. 卫星的机械能一定相等D. 卫星也可能相对地面静止11. 如图所示，实线表示电场线，虚线表示只受电场力作用的带电粒子的运动轨迹，粒子先经过点，再经过点。

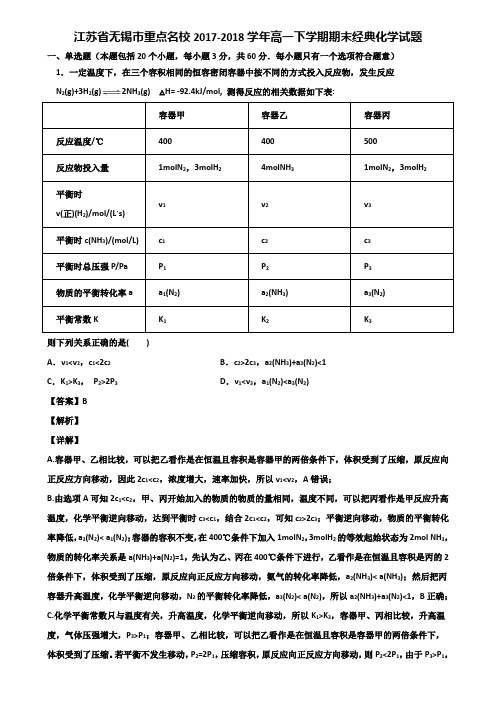
江苏省无锡市重点名校2017-2018学年高一下学期期末经典化学试题一、单选题（本题包括20个小题，每小题3分，共60分．每小题只有一个选项符合题意）1．一定温度下，在三个容积相同的恒容密闭容器中按不同的方式投入反应物，发生反应N 2(g)+3H2(g)2NH3(g) △H= -92.4kJ/mol, 测得反应的相关数据如下表:容器甲容器乙容器丙反应温度/℃400 400 500反应物投入量1molN2，3molH24molNH31molN2，3molH2平衡时v1v2v3v(正)(H2)/mol/(L·s)平衡时c(NH3)/(mol/L) c1c2c3平衡时总压强P/Pa P1P2P3物质的平衡转化率a a1(N2) a2(NH3) a3(N2)平衡常数K K1K2K3则下列关系正确的是( )A．v1<v2，c1<2c2B．c2>2c3，a2(NH3)+a3(N2)<1C．K1>K3，P2>2P3D．v1<v3，a1(N2)<a3(N2)【答案】B【解析】【详解】A.容器甲、乙相比较，可以把乙看作是在恒温且容积是容器甲的两倍条件下，体积受到了压缩，原反应向正反应方向移动，因此2c1<c2，浓度增大，速率加快，所以v1<v2，A错误；B.由选项A可知2c1<c2，甲、丙开始加入的物质的物质的量相同，温度不同，可以把丙看作是甲反应升高温度，化学平衡逆向移动，达到平衡时c3<c1，结合2c1<c2，可知c2>2c3；平衡逆向移动，物质的平衡转化率降低，a3(N2)< a1(N2)；容器的容积不变，在400℃条件下加入1molN2，3molH2的等效起始状态为2mol NH3，物质的转化率关系是a(NH3)+a(N2)=1，先认为乙、丙在400℃条件下进行，乙看作是在恒温且容积是丙的2倍条件下，体积受到了压缩，原反应向正反应方向移动，氨气的转化率降低，a2(NH3)< a(NH3)；然后把丙容器升高温度，化学平衡逆向移动，N2的平衡转化率降低，a3(N2)< a(N2)，所以a2(NH3)+a3(N2)<1，B正确；C.化学平衡常数只与温度有关，升高温度，化学平衡逆向移动，所以K1>K3，容器甲、丙相比较，升高温度，气体压强增大，P3>P1；容器甲、乙相比较，可以把乙看作是在恒温且容积是容器甲的两倍条件下，体积受到了压缩。

江苏省无锡市2017-2018学年高一英语下学期期末考试试题第一卷(共95分）一、听力测试(共两节,满分20分）做题时,先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题纸/卡上。

第一节（共5小题；每小题1分，满分5分）听下面5段对话。

每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题.每段对话仅读一遍.1。

What does the man think of his friend Sam？A. Selfish。

B. Kind-hearted。

C. Open-minded.2. What time is it now？A。

8:00。

B。

7:45。

C.8:15.3. How long does the man plan to work in Germany？A. One year.B. Half a year。

C. One and a half years.4. How d oes the man feel about Tom’s behavior at the meeting?A。

Angry。

B. Excited. C. Worried. 5。

What can we know about Jenny？A. She failed to attend class today.B. She is in hospital now.C. She is feeling terrible now。

第二节(共15小题；每小题1分，满分15分）听下面5段对话或独白。

每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置.听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间.每段对话或独白读两遍.听第6段材料,回答第6至7题.6。

【全国百强校】江苏省无锡市第一中学【最新】高一下学期期末考试数学试题学校:___________姓名：___________班级：___________考号：___________一、填空题1．某校有老师200人，男学生1200人，女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为120人的样本进行某项调查，则应抽取的男学生人数为 ． 2．等比数列{}n a 中，若21a =，58a =，则7a = ．3．在ABC ∆中，3A π∠=，3BC =，AB =C ∠= ．4．如图，有四根木棒穿过一堵墙，两人分别站在墙的左、右两边，各选该边的一根木棒.若每边每根木棒被选中的机会相等，则两人选到同一根木棒的概率为__________．5．已知某人连续5次射击的环数分别是8，9，10，x ，8，若这组数据的平均数是9，则这组数据的方差为 ．6．如图所示是一算法的伪代码，执行此算法时，输出的结果是 ．7．已知实数x ，y 满足,2,0,y x x y x ≥⎧⎪+≤⎨⎪≥⎩则93x y z =⋅的最大值是 ．8．在等差数列{}n a 中，0n a >，45a =，则2619a a +的最小值为 ．9．设()()11111223341n S n N n n *=++++∈⨯⨯⨯+，且156n n S S +=，则n = ．10．如图所示，墙上挂有一块边长为a 的正六边形木板，它的六个角的空白部分都是以正六边形的顶点为圆心，半径为2a 的扇形面，某人向此板投镖一次，假设一定能击中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是__________．11．在ABC ∆中，已知3C π∠=，BC a =，AC b =，且a ，b 是方程213400x x -+=的两根，则AB 的长度为 ．12．在R 上定义运算a ※()1b a b =+，若存在[]1,2x ∈，使不等式()m x -※()4m x +<成立，则实数m 的取值范围为 ．13．设数列{}n a 的前n 项和为n S ，()22n n n S n N *-=∈，若对任意实数[]0,1λ∈，总存在自然数k ，使得当n k ≥时，不等式()()2123243n n n a a λλλ+-≥-++恒成立，则k 的最小值是 ．14．已知0x >，0y >，则2222629xy xy x y x y +++的最大值是 ．二、解答题15．某校有500名学生参加学校组织的“数学竞赛集训队”选拔考试，现从中等可能抽出n 名学生的成绩作为样本，制成如图频率分布表：（1）求n 的值，并根据题中信息估计总体平均数是多少？（2）若成绩不低于135分的同学能参加“数学竞赛集训队”，试估计该校大约多少名学生能参加“数学竞赛集训队”？16．在ABC 中，角,,A B C 的对边分别是,,a b c ，若cos sin 3a b C c B =+． （1）求角B 的值；（2）若ABC 的面积S =5a =，求b 的值．17．已知数列{}n a 是首项为12，公比为()1q q ≠的等比数列，且1a ，232a ，32a 成等差数列.（1）求数列{}n a 的通项公式；（2）若n n b na =，记数列{}n b 的前n 项和为n T ，求满足不等式16300n T n +-≤的最大正整数n 的值.18．如图所示，ABC ∆是临江公园内一个等腰三角形．．．．．形状的小湖（假设湖岸是笔直的），其中两腰60CA CB ==米，2cos 3CAB ∠=.为了给市民营造良好的休闲环境，公园管理处决定在湖岸AC ，AB 上分别取点E ，F （异于线段端点），在湖上修建一条笔直的水上观光通道EF （宽度不计），使得三角形AEF 和四边形BCEF 的周长相等.（1）若水上观光通道的端点E 为线段AC 的三等分点（靠近点C ），求此时水上观光通道EF 的长度；（2）当AE 为多长时，观光通道EF 的长度最短？并求出其最短长度.19．已知函数()()2223,0f x x mx m m R m =--∈>. （1）解关于x 的不等式()22f x mx m x >+；（2）若当[]1,4x m ∈时，()4f x m ≤恒成立，求实数m 的取值范围.20．已知等差数列{}n a 的前n 项的和为n S ，公差0d ≠，若4a ，6a ，10a 成等比数列，714S =；数列{}n b 满足：对于任意的*n N ∈，等式1213212n n n n b a b a b a b a n --++++=-都成立.（1）求数列{}n a 的通项公式；（2）证明：数列{}n b 是等比数列；（3）若数列{}n c 满足2lg n n na cb +=，试问是否存在正整数s ，t （其中1s t <<），使1c ，s c ，t c 成等比数列？若存在，求出所有满足条件的数组(),s t ；若不存在，请说明理由.参考答案1．60【解析】分析：直接利用分层抽样的定义求解. 详解：由题得应抽取的男学生人数为12001206020012001000⨯=++.故答案为：60. 点睛：(1)本题主要考查分层抽样，意在考查学生对该基础知识的掌握水平.(2) 当已知总体由差异明显的几部分组成时，为了使样本充分地反映总体的情况，常将总体分成几部分，然后按照各部分所占的比例进行抽样,这种抽样叫分层抽样.2．32【解析】分析：利用已知求出首项1a 和公比q,再求7a . 详解：由题得114111,, 2.82a q a q a q =⎧∴==⎨=⎩所以671()2322a =⋅=.故答案为：32. 点睛：（1）本题主要考查等比数列的通项的求法，意在考查学生对这些基础知识的掌握水平.(2) 等比数列的通项公式：111(0)n n m n m a a q a q a q --==≠.3．4π 【解析】分析：直接利用正弦定理求∠C.33,3sin sin .44sin 3C C C πππ=∴=∴=∴=或 因为AB ＜BC ，所以∠C ＜∠A=3π,所以4C π∠=.故答案为：4π. 点睛：（1）本题主要考查正弦定理解三角形，意在考查学生对该基础知识的掌握水平.(2) 解三角形如果出现多解，要利用三角形内角和定理或三角形边角不等关系来检验.4．14【解析】分析：直接利用古典概型求解.详解：由古典概型得两人选到同一根木棒的概率为141444C P ==⨯.故答案为14. 点睛：（1）本题主要考查古典概型，意在考查学生对该基础知识的掌握水平.(2) 古典概型的解题步骤:①求出试验的总的基本事件数n ；②求出事件A 所包含的基本事件数m ；③代公式()P A =A m n=包含的基本事件数总的基本事件个数. 5．45【解析】分析：先根据平均数求x 的值，再求数据的方差. 详解：由题得8+9+8109,10.5x x ++=∴= 所以数据的方差为22222214[(89)(99)(109)(109)(89)]55S =-+-+-+-+-=.故答案为45. 点睛：（1）本题主要考查平均数和方差的计算，意在考查学生对这些基础知识的掌握水平.(2) 方差公式为222121[()()()]n S x x x x x x n =-+-+⋅⋅⋅+-. 6．3【解析】根据题中的程序框图，可得该程序经过第一次循环，因为s =0<15，所以得到新的S =0+6=6，n =5；然后经过第二次循环，因为s =6<15，所以得到新的S =6+5=11，n =4；然后经过第三次循环，因为s =11<15，所以得到新的S =11+4=15，n =3；接下来判断：因为s =15，不满足s <15，所以结束循环体并输出最后的n ，综上所述，可得最后输出的结果是3故答案为37．27【解析】分析:先化简93x y z =⋅=22333x y x y +⋅=，再作出不等式组对应的可行域，再利用数形结合分析得到z 的最大值.详解:由题得93x y z =⋅=22333x y x y +⋅=.不等式组对应的可行域如图所示的△OAB ，设u=2x+y,则y=-2x+u,当直线y=-2x+u 经过点A(1,1)时，直线的纵截距最大，u 最大=2×1+1=3， 所以3max 327z ==.故答案为：27.点睛：（1）本题主要考查线性规划，意在考查学生对这些基础知识的掌握水平和数形结合的思想方法.(2) 解答线性规划时，要加强理解，不是纵截距最小，z 就最小，要看函数的解析式，如：2y x z =-,直线的纵截距为z -,所以纵截距z -最小时，z 最大.8．85【解析】分析：先求出264210,a a a +==再利用基本不等式求2619a a +的最小值. 详解：由题得264210,a a a +== 所以2619a a +=2619a a +（）2626119110()()1010a a a a ⨯⨯=++⨯62269118(10)(10.10105a a a a =++≥+= 故2619a a +的最小值为85.故答案为：85.点睛：（1）本题主要考查基本不等式，意在考查学生对该基础知识的掌握水平和转化能力.(2) 本题的解题关键是常量代换，即把2619a a +化成2626191()()10a a a a ++⨯，再利用基本不等式求函数的最小值.9．10【解析】 分析：先化简n S ，再根据156n n S S +=求n 的值. 详解：由题得111111*********n n S n n n n =-+-++-=-=+++. 因为156n n S S +=，所以15,10.126n n n n n +⨯=∴=++ 点睛：（1）本题主要考查裂项相消求和，意在考查学生第该知识的掌握水平和基本的运算能力.(2) 类似1n n c a a +⎧⎫⎨⎬⎩⎭（其中{}n a 是各项不为零的等差数列，c 为常数）的数列、部分无理数列等.用裂项相消法求和.10．19- 【解析】分析：先计算出正六边形的面积，再求出阴影部分的面积，最后利用几何概型求击中阴影部分的概率.详解：由题得正六边形的面积为226.aa = 22222().22a a a ππ-⨯⨯=-221a π-=.故答案为1-. 点睛：（1）本题主要考查几何概型，意在考查学生对这些基础知识的掌握水平.(2) 几何概型的解题步骤:首先是判断事件是一维问题还是二维、三维问题（事件的结果与一个变量有关就是一维的问题，与两个变量有关就是二维的问题，与三个变量有关就是三维的问题）；接着，如果是一维的问题，先确定试验的全部结果和事件A 构成的区域长度（角度、弧长等），最后代公式()A P A =构成事件的区域长度试验的全部结果所构成的区域长度；如果是二维、三维的问题，先设出二维或三维变量，再列出试验的全部结果和事件A 分别满足的约束条件，作出两个区域，最后计算两个区域的面积或体积代公式.11．7【解析】分析：先根据已知求出a+b,ab 的值，再利用余弦定理求AB 的值.详解：因为a ，b 是方程213400x x -+=的两根，所以13,40.a b ab +==由余弦定理得22202222cos 60()316912049.c a b ab a b ab a b ab =+-=+-=+-=-=所以AB=7.故答案为：7.点睛：（1）本题主要考查余弦定理，意在考查学生对该基础知识的掌握水平和分析推理能力.(2)本题可以求出a,b 的值，也可以整体代入求值,本题的解法就是整体代入求值. 12．()3,2-【解析】分析：先利用定义运算化简得到存在[]1,2x ∈，使不等式()1m x -+×()4m x +<成立，再化简得到存在[]1,2x ∈，使不等式224x x m m -+>+成立，最后得到26m m >+，解不等式即得m 的取值范围.详解：因为存在[]1,2x ∈，使不等式()m x -※()4m x +<成立，所以存在[]1,2x ∈，使不等式()1m x -+×()4m x +<成立，所以存在[]1,2x ∈，使不等式224x x m m -+>+成立，因为x ∈[1,2],所以函数24y x x =-+的最大值为22246-+=.所以26,3 2.m m m >+∴-<<故答案为（-3,2）.点睛：（1）本题主要考查新定义和存在性问题，意在考查学生对这些基础知识的掌握水平和分析推理能力.(2)本题利用到了分离参数法，其中转化为存在[]1,2x ∈，使不等式224x x m m -+>+成立是关键.处理参数的问题常用的有分离参数法和分类讨论法. 13．5【解析】 分析：先根据22n n n S -=求出1,n a n =-再把1n a n =-代入不等式化简得对任意实数[]0,1λ∈，2(21)430n n n λ-+--≥恒成立，再利用数形结合分析得到k 的最小值. 详解：因为22n n n S -=，所以n≥2时，21(1)(1),2n n n S ----= 所以11,n n n S S a n --==-适合n=1.所以 1.n a n =-因为对任意实数[]0,1λ∈，不等式()()2123243n n n a a λλλ+-≥-++恒成立， 所以对任意实数[]0,1λ∈，()()22324n 1n 3n λλλ-≥--++（）恒成立， 所以对任意实数[]0,1λ∈，2(21)430n n n λ-+--≥恒成立， 令2()(21+43f n n n λλ=---）， 所以22(0)430, 5.(1)21430f n n n f n n n ⎧=--≥∴≥⎨=-+--≥⎩所以k 的最小值为5.故答案为：5.点睛：（1）本题主要考查数列通项的求法和不等式恒成立问题，意在考查学生对这些基础知识的掌握水平和分析推理能力.(2)解答本题的关键有两点，其一是把原命题转化为对任意实数[]0,1λ∈，2(21)430n n n λ-+--≥恒成立，其二是通过数形结合分析得到22(0)430(1)21430f n n f n n n ⎧=--≥⎨=-+--≥⎩.14【解析】分析：先化简原式为629x yx y y x y x+++，再换元设(0)x t t y=>得原式2238()910t t t t+=++，再换元设3(0)u t t t=+>得原式84u u=+，再利用函数单调性得到函数的最大值. 详解：由题得原式=629xy x y y xy x+++，设(0)xt t y =>， 所以原式=322422238()62628(3)9199110910t t t t t t t t t t t t t t t t +++=+==++++++++，令3(0),u t t u t=+>∴≥所以原式=288884484u u u u =≤==++.(函数在)+∞上单调递减)..点睛：(1)本题主要考查基本不等式，考查函数y=x+1x的图像和性质，考查换元法的运用，意在考查学生对这些知识的掌握水平和分析转化的能力及数形结合的思想方法.(2)解答本题的关键是两次换元，第一次是设(0)x t t y =>，第二次是设3(0),u t t t=+>换元一定要注意新元的范围.15．（1）见解析；（2）75人. 【解析】分析：（1）根据120.3n=求出n 的值，再根据频率分布直方图平均数公式求总体的平均数.(2)先求成绩不低于135分的同学的概率，再求该校大约多少名学生能参加“数学竞赛集训队”. 详解：（1）由第四行数据可知120.3n=，所以40n =. 数据[)135,145的频率为()10.0250.050.20.30.2750.050.1-+++++=， 则利用组中值估计平均数为900.0251000.051100.21200.31300.2751400.11500.05122.5⨯+⨯+⨯+⨯+⨯+⨯+⨯=.（2）成绩不低于135分的同学的概率为0.10.050.15+=， ∴该校能参加集训队的人数大约为5000.15=75⨯人.点睛：（1）本题主要考查频率分布直方图中概率和平均数的计算，意在考查学生对这些基础知识的掌握水平和分析解决实际问题的能力.(2) E ξ=11x p +22x p +…n n x p ++… 为ξ的均值或数学期望，简称期望．16．(1) 3B π=;(2) b =.【解析】分析：（1）利用正弦定理边化角化简cos sin 3a b C B =+得到B 的值.(2)先求c 的值，再利用余弦定理求b 的值.详解：（1）由cos sin a b C B =及正弦定理得：sin sin cos sin A B C C B =+，① 又()sin sin sin cos cos sin A B C B C B C =+=+，②由①②得cos sin sin B C C B =，在ABC ∆中，∵sin 0C ≠，∴cos B B =，∴tan B =()0,B π∈，∴3B π=.（2）由11sin 22S ac B ====20ac =. 又5a =，所以4c =.由余弦定理，得2222cos 25162021b a c bc A =+-=+-=，故b =.点睛：（1）本题主要考查正弦定理余弦定理解三角形，意在考查学生对这些基础知识的掌握水平和分析推理的能力.(2)化简三角等式时，一般利用正弦定理和余弦定理实行角化边或边化角，本题的解答就是利用正弦定理边化角，也可以角化边.17．(1) 1112nn n a a q -⎛⎫== ⎪⎝⎭;(2) 正整数n 的最大值为4. 【解析】分析：（1）根据1a ，232a ，32a 成等差数列求出q ，即得数列{}n a 的通项公式.(2)先利用错位相减法求出数列{}nb 的前n 项和n T ，再把n T 代入不等式16300n T n +-≤化简即得最大正整数n 的值.详解：（1）由题意得1323222a a a +=⋅， ∴211123222q q +⋅=⋅⋅，即22310q q -+=，解得1q =或12q =. 又1q ≠，于是12q =，∴1112nn n a a q-⎛⎫== ⎪⎝⎭. （2）12nn n b na n ⎛⎫== ⎪⎝⎭， 12311111232222nn T n ⎛⎫⎛⎫⎛⎫⎛⎫=++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，2311111122222n n T n +⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.两式相减得：231111111222222nn n T n +⎛⎫⎛⎫⎛⎫⎛⎫=++++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，()1111111122212122212nn n n T n n ++⎛⎫-⋅ ⎪⎛⎫⎛⎫⎝⎭=-=-+ ⎪ ⎪⎝⎭⎝⎭-， ∴()1222nn T n ⎛⎫=-+ ⎪⎝⎭. ∴16300n T n +-≤转化为11216n⎛⎫≥ ⎪⎝⎭， ∴4n ≤.∴正整数n 的最大值为4.点睛：（1）本题主要考查等比数列通项的求法，考查错位相减法求数列的和，考查不等式的恒成立问题，意在考查学生对这些基础知识的掌握水平和分析推理转化的能力.(2) 若数列{}·n n b c ，其中{}n b 是等差数列，{}n c 是等比数列，则采用错位相减法.18．(1) 水上观光通道EF 的长度为;(2) 当50AE =米时，水上观光通道EF 的长米. 【解析】分析：（1）在等腰ABC ∆中，过点C 作CH AB ⊥于H ，先计算出40E =，60AF =，再利用余弦定理求出EF 的长度.(2) 设AE x =，AF y =，先求出EF 的表达式，再利用基本不等式求其最短长度.详解：（1）在等腰ABC ∆中，过点C 作CH AB ⊥于H ，在Rt ACH ∆中，由cos AH CAB AC ∠=，即2603AH =，∴40AH =，80AB =， ∴三角形AEF 和四边形BCEF 的周长相等. ∴AE AF EF CE BC BF EF ++=+++，即()()606080AE AF AE AF +=-++-，∴100AE AF +=.∵E 为线段AC 的三等分点（靠近点C ），∴40AE =，60AF =， 在AEF ∆中，2222222cos 4060240602003EF AE AF AE AF CAB =+-⋅∠=+-⋅⋅⋅=，∴EF ==米.即水上观光通道EF 的长度为.（2）由（1）知，100AE AF +=，设AE x =，AF y =，在AEF ∆中，由余弦定理，得()2222224102cos 33EF x y x y CAB x y xy x y xy =+-⋅∠=+-=+-.∵22502x y xy +⎛⎫≤= ⎪⎝⎭，∴()2222102100505033EF ≥-⨯=⨯.∴EF ≥，当且仅当x y =取得等号，所以，当50AE =米时，水上观光通道EF 的长度取得最小值，最小值为3米. 点睛：（1）本题主要考查利用余弦定理解三角形，考查利用基本不等式求函数的最小值，意在考查学生对这些基础知识的掌握水平和分析推理能力.(2) 基本不等式有三种形式，本题利用的是2()2a b ab +≤（当且仅当a=b 时取等）. 19．(1) 当01m <<时，不等式解集为31m x x m x m 或⎧⎫--⎨⎬-⎩⎭；当1m =时，不等式解集为{}1x x <-；当14m <<时，不等式解集为31mx x m m ⎧⎫-<<-⎨⎬-⎩⎭；当4m =时，不等式解集为ϕ；当4m >时，不等式解集为31m x m x m ⎧⎫-<<-⎨⎬-⎩⎭;(2) m 的取值范围是14,45⎛⎤ ⎥⎝⎦. 【解析】分析：（1）对m 分类讨论，利用一元二次不等式的解法解不等式()22f x mx m x >+.(2)对m 分类讨论，求()f x 的最大值，再令()f x 的最大值小于等于4m ，即得m 的取值范围. 详解：（1）由题意，得()()2221230m x m m x m -+++<即()()130m x m x m ⎡⎤-++<⎣⎦①当1m =时，得10x +<，解得1x <-； ②当01m <<时，得()301m x x m m ⎛⎫++> ⎪-⎝⎭， ∵()()24340111m m m m m m m m m -----==>---， ∴31m m m ->--解得x m <-或31mx m >--； ③当1m >时，得()301m x x m m ⎛⎫++< ⎪-⎝⎭，∵()()2434111m m m m m m m m m -----==---. 当4m >时，31m m m ->--，解得31mm x m -<<--； 当4m =时，31m m m -=--，()240x +<，解集为空集； 当14m <<时，31m m m -<--，解得31mx m m -<<--； 综上所述：当01m <<时，不等式解集为31m x x m x m ⎧⎫--⎨⎬-⎩⎭或； 当1m =时，不等式解集为{}1x x <-；当14m <<时，不等式解集为31m x x m m ⎧⎫-<<-⎨⎬-⎩⎭；当4m =时，不等式解集为ϕ；当4m >时，不等式解集为31m x m x m ⎧⎫-<<-⎨⎬-⎩⎭. （2）()2223f x x mx m =--的图像是一条开口向上的抛物线，关于x m =对称.由题意：14m >. ①若114m <≤，则()f x 在[]1,4m 上是增函数，从而 ()f x 在[]1,4m 上的最小值是()21123f m m =--，最大值是()245f m m =.由()4f x m ≤得224234m x mx m m -≤--≤于是有()()2211234454f m m m f m m m ⎧=--≥-⎪⎨=≤⎪⎩解得113405m m ⎧-≤≤⎪⎪⎨⎪≤≤⎪⎩，∴405m <≤. 又∵114m <≤，∴1445m <≤. ②若1m >，此时()2454f m m m =>. 则当14x m ≤≤时，()4f x m ≤不恒成立.综上：使()[]()41,4f x m x m ≤∈恒成立的m 的取值范围是14,45⎛⎤⎥⎝⎦. 点睛：（1）本题主要考查一元二次不等式的解法，考查不等式的恒成立问题，意在考查学生对这些基础知识的掌握水平和分析推理能力,考查分类讨论思想方法.(2)解答本题的关键是求求()f x 的最大值，这里利用了二次函数的图像和性质，利用了数形结合的思想方法. 20．(1) 2n a n =-;(2)见解析；（3）见解析. 【解析】分析：（1）根据已知解方程组得11,1,a d =-⎧⎨=⎩，即得数列{}n a 的通项公式.（2）利用作差法化简1213212n n n n b a b a b a b a n --++++=-即得()*212n n b n N b ++=∈，即证明数列{}n b 是等比数列.(3)先化简2lg n n na cb +=,再化简1c ，s c ，t c 成等比数列,对s 分类讨论得解. 详解：（1）设数列{}n a 公差为d ，由题设得264107,14,a a a S ⎧=⋅⎨=⎩ 即()()()21111539,72114,a d a d a d a d ⎧+=+⋅+⎪⎨+=⎪⎩解得11,1,a d =-⎧⎨=⎩ ∴数列{}n a 的通项公式为：2n a n =-. （2）∵1213212n n n n b a b a b a b a n --++++=-∴()()()()12323412n b n b n b n b n -+-+-++-=-，①∴()()()()()12311230121n n b n b n b n b b n +-+-+-++⋅+-=-+，②由②-①得12312n n b b b b b +++++-=-，③∴123122n n n b b b b b b +++++++-=-，④由④-③得122n n b b ++=， 由①知12b =，240b =≠，∴()*212n n b n N b ++=∈.又212b b =，∴数列{}n b 是等比数列. （3）假设存在正整数s ，t （其中1s t <<），使1c ，s c ，t c 成等比数列，则1lg c ，lg s c ，lg t c 成等差数列.由（2）可知：2nn b =，∴2lg 2n n n n a nc b +==. 于是，12222s t s t⋅=+. 由于02t t >，所以1122224s s s s ⋅>⇒>因为当2n ≥时，11110222n n n n n n +++--=<，即2n n单调递减，所以当4s ≥时，441224s s ≤=，不符合条件，所以2s =或3s =， 又1s t <<，所以3t ≥，所以333228t t ≤= 当2s =时，得122t t =，无解， 当3s =时，得124t t =，所以4t =，综上：存在唯一正整数数组()(),3,4s t =，使1c ，s c ，t c 成等比数列.点睛：（1）本题主要考查数列通项的求法，考查数列性质的证明，考查数列的探究性问题，意在考查学生对这些基础知识的掌握水平和分析推理能力转化能力.(2)解答本题的难点在第3问，其解答关键是对s 的分类讨论和分析.。

2017/2018学年度第二学期高一年级期终考试数学试题参考公式：锥体体积公式：，其中为底面积，为高．一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．1. 函数的最小正周期为______．2. 已知直线过定点，且倾斜角为，则直线的一般式方程为______．3. 若，则______．4. 在中，，，，则______．5. 设等差数列的前项和为，若首项，公差，，则正整数=______．6. 设、表示两条直线，、表示两个平面，则下列命题正确的是______．（填写所有正确命题的序号）①若//，//，则//；②若//，，，则；③若//，，则；④若，，，则．7. 已知正项等比数列，且，则______．8. 若圆锥的侧面展开图是半径为、圆心角为的扇形，则该圆锥的体积为______．9. 已知向量a是与向量b＝(－3,4)同向的单位向量，则向量a的坐标是______．10. 已知函数是奇函数，则的最小值为______．11. 在平面直角坐标系中，以点（1,0）为圆心且与直线相切的所有圆中，半径最大的圆的标准方程为______．12. 已知数列满足（），若，则______．13. 如图，点是正六边形的边上的一个动点，设，则的最大值为______．14. 在锐角中，角、、的对边分别为、、，若，则的取值范围是______．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15. 如图，已知平行四边形ABCD中，BC＝6，正方形ADEF所在平面与平面ABCD垂直，G、H分别是DF、BE的中点．（1）求证：GH//平面CDE；（2）若CD＝2，DB＝4，求四棱锥F－ABCD的体积．16. 已知向量和，其中，，．（1）当为何值时，有//；（2）若向量与的夹角为钝角，求实数的取值范围．学￥科￥网...17. 如图，在平面直角坐标系中，点是圆：与轴正半轴的交点，半径OA在轴的上方，现将半径OA绕原点O逆时针旋转得到半径OB．设()，．（1）若，求点的坐标；（2）求函数的最小值，并求此时的值．18. 如图，、是两条公路（近似看成两条直线），，在内有一纪念塔（大小忽略不计），已知到直线、的距离分别为、，=6千米，=12千米．现经过纪念塔修建一条直线型小路，与两条公路、分别交于点、．（1）求纪念塔到两条公路交点处的距离；（2）若纪念塔为小路的中点，求小路的长．19. 设无穷等差数列的前项和为，已知，．（1）求与的值；（2）已知、均为正整数，满足．试求所有的值构成的集合．20. 如图，已知动直线过点，且与圆交于、两点．（1）若直线的斜率为，求的面积；（2）若直线的斜率为，点是圆上任意一点，求的取值范围；（3）是否存在一个定点（不同于点），对于任意不与轴重合的直线，都有平分，若存在，求出定点的坐标；若不存在，请说明理由．一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．1. 函数的最小正周期为______．【答案】【解析】由三角函数的最小正周期公式可得：函数的最小正周期为 .2. 已知直线过定点，且倾斜角为，则直线的一般式方程为______．【答案】【解析】直线的斜率，则直线的一般式方程为：，整理为一般式为：.3. 若，则______．【答案】【解析】由诱导公式可得：，由二倍角公式有： .4. 在中，，，，则______．【答案】9【解析】如图所示，由平面向量数量积的定义可得：.点睛：求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．5. 设等差数列的前项和为，若首项，公差，，则正整数=______．【答案】5【解析】由等差数列的前n项和公式可得：，则：，据此可得正整数=5.6. 设、表示两条直线，、表示两个平面，则下列命题正确的是______．（填写所有正确命题的序号）①若//，//，则//；②若//，，，则；③若//，，则；④若，，，则．学&科&网...【答案】②③【解析】①中，有可能直线b位于平面内，该说法错误；②中的结论符合面面垂直的推论，该说法正确；③中的结论符合面面垂直的推论，该说法正确；④若直线均在平面内，则或，该结论错误.综上可得命题正确的是②③.7. 已知正项等比数列，且，则______．【答案】5【解析】考点：等比数列的性质。

江苏省无锡市普通高中2017—2018学年高一语文下学期期末考试试题
（扫描版)
尊敬的读者：
本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

2017-2018学年江苏省无锡市高一（下）期末数学试卷一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．）1．（5分）某校有老师200人，男学生1200人，女学生1000人，现用分层抽样的方法从所有师生中抽取一个容量为120人的样本进行某项调查，则应抽取的男学生人数为．2．（5分）等比数列{a n}中，若a2＝1，a5＝8，则a7＝．3．（5分）△ABC中，，BC＝3，，则∠C＝．4．（5分）如图，有四根木棒穿过一堵墙，两人分别站在墙的左、右两边，各选该边的一根木棒．若每边每根木棒被选中的机会相等，则两人选到同一根木棒的概率为．5．（5分）已知某人连续5次射击的环数分别是8，9，10，x，8，若这组数据的平均数是9，则这组数据的方差为．6．（5分）如图所示是一算法的伪代码，执行此算法时，输出的结果是．7．（5分）已知实数x，y满足，则z＝9x•3y的最大值是．8．（5分）在等差数列{a n}中，a n＞0，a4＝5，则的最小值为．9．（5分）设，且，则n ＝．10．（5分）如图所示，墙上挂有一块边长为a的正六边形木板，它的六个角的空白部分都是以正六边形的顶点为圆心，半径为的扇形面，某人向此板投镖一次，假设一定能击中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是．11．（5分）在△ABC中，已知∠C＝，BC＝a，AC＝b，且a，b是方程x2﹣13x+40＝0的两根，则AB的长度为．12．（5分）在R上定义运算a※b＝（a+1）b，若存在x∈[1，2]，使不等式（m﹣x）※（m+x）＜4成立，则实数m的取值范围为．13．（5分）设数列{a n}的前n项和为S n，，若对任意实数λ∈[0，1]，总存在自然数k，使得当n≥k时，不等式（2λ﹣3）n2≥（2λ﹣4）a n a n+1+λ+3恒成立，则k的最小值是．14．（5分）已知x＞0，y＞0，则+的最大值是．二、解答题（本大题共6小题，共计90分．请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤．）15．（14分）某校有500名学生参加学校组织的“数学竞赛集训队”选拔考试，现从中等可能抽出n名学生的成绩作为样本，制成如图频率分布表：（1）求n的值，并根据题中信息估计总体平均数是多少？（2）若成绩不低于135分的同学能参加“数学竞赛集训队”，试估计该校大约多少名学生能参加“数学竞赛集训队”？16．（14分）在△ABC中，角A，B，C的对边分别是a，b，c，若．（1）求角B的值；（2）若△ABC的面积S＝，a＝5，求b的值．17．（14分）已知数列{a n}是首项为，公比为q（q≠1）的等比数列，且a1，，2a3成等差数列．（1）求数列{a n}的通项公式；（2）若b n＝na n，记数列{b n}的前n项和为T n，求满足不等式16T n+n﹣30≤0的最大正整数n的值．18．（16分）如图所示，△ABC是临江公园内一个等腰三角形形状的小湖（假设湖岸是比值的），其中两腰CA＝CB＝60米，cos∠CAB＝．为了给市民营造良好的休闲环境，公园管理处决定在湖岸AC，AB上分别取点E，F（异于线段端点），在湖上修建一条笔直的水上观光通道EF（宽度不计），使得三角形AEF和四边形BCEF的周长相等．（1）若水上观光通道的端点E为线段AC的三等分点（靠近点C），求此时水上观光通道EF的长度；（2）当AE为多长时，观光通道EF的长度最短？并求出其最短长度．19．（16分）已知函数f（x）＝x2﹣2mx﹣3m2（m∈R，m＞0）．（1）解关于x的不等式f（x）＞mx2+m2x；（2）若当x∈[1，4m]时，|f（x）|≤4m恒成立，求实数m的取值范围．20．（16分）已知等差数列{a n}的前n项的和为S n，公差d≠0，若a4，a6，a10成等比数列，S7＝14，数列{b n}满足：对于任意的n∈N*，等式b1a n+b2a n﹣1+b3a n﹣2+…+b n a1＝﹣2n都成立．（1）求数列{a n}的通项公式；（2）证明：数列{b n}是等比数列；（3）若数列{c n}满足，试问是否存在正整数s，t（其中1＜s＜t），使c1，c s，c t成等比数列？若存在，求出所有满足条件的数组（s，t）；若不存在，请说明理由．2017-2018学年江苏省无锡市高一（下）期末数学试卷参考答案与试题解析一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．）1．【考点】B3：分层抽样方法．【解答】解：分层抽样的抽取比例为：＝，∴男生中抽取的人数为1200×＝60．故答案为：60．【点评】本题考查分层抽样，分层抽样的优点是：使样本具有较强的代表性，并且抽样过程中可综合选用各种抽样方法，因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法．2．【考点】88：等比数列的通项公式．【解答】解：等比数列{a n}中，若a2＝1，a5＝8，∴a5＝a2q3，∴q3＝8，∴q＝2，则a7＝a5q2＝8×4＝32，故答案为：32【点评】本题考查了等比数列的通项公式，考查了运算能力，属于基础题．3．【考点】HP：正弦定理．【解答】解：由，a＝BC＝3，c＝，根据正弦定理＝得：sin C＝＝，又C为三角形的内角，且c＜a，∴0＜∠C＜，则∠C＝．故答案为：【点评】此题考查了正弦定理，以及特殊角的三角函数值，正弦定理很好的建立了三角形的边角关系，熟练掌握正弦定理是解本题的关键，同时注意判断C的范围．4．【考点】CC：列举法计算基本事件数及事件发生的概率．【解答】解：有四根木棒穿过一堵墙，两人分别站在墙的左、右两边，各选该边的一根木棒．基本事件总数n＝4×4＝16，每边每根木棒被选中的机会相等，两人选到同一根木棒包含的基本事件个数m＝4，∴两人选到同一根木棒的概率为p＝＝＝．故答案为：．【点评】本题考查概率的求法，考查古典概型等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．5．【考点】BC：极差、方差与标准差．【解答】解：根据题意，数据8，9，10，x，8的平均数是9，则有（8+9+10+x+8）＝45，解可得：x＝10，则这组数据的方差S2＝[（8﹣9）2+（9﹣9）2+（10﹣9）2+（10﹣9）2+（8﹣9）2]＝0.8；故答案为：0.8【点评】本题考查数据的方差计算，关键是由平均数公式求出x的值．6．【考点】EA：伪代码（算法语句）．【解答】解：根据题中的程序框图，可得该程序经过第一次循环，因为s＝0＜15，所以得到新的S＝0+6＝6，n＝5；然后经过第二次循环，因为s＝6＜15，所以得到新的S＝6+5＝11，n＝4；然后经过第三次循环，因为s＝11＜15，所以得到新的S＝11+4＝15，n＝3；接下来判断：因为s＝15，不满足s＜15，所以结束循环体并输出最后的n，综上所述，可得最后输出的结果是3故答案为：3【点评】本题给出程序框图，求最后输出的n值，属于基础题．解题的关键是先根据已知条件判断程序的功能，构造出相应的数学模型再求解，从而使问题得以解决．7．【考点】7C：简单线性规划．【解答】解：画实数x，y满足可行域如图，z为目标函数z＝9x•3y＝32x+y，u ＝2x+y的纵截距取得最大值时，z取得最大值，画直线L：0＝2x+y，平移直线过A时z有最大值，由可得A（1，1），此时u＝3，z＝27．故答案为：27．【点评】本题考查线性规划问题，难度较小．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．8．【考点】83：等差数列的性质．【解答】解：∵在等差数列{a n}中，a n＞0，a4＝5，∴a2+a6＝2a4＝10，∴＝（）（a2+a6）＝（++10）≥＝1.6．当且仅当＝时，取等号．故的最小值为1.6．故答案为：1.6．【点评】本题考查代数式的最小值的求法，考查等差数列、基本不等式的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．9．【考点】8E：数列的求和．【解答】解：＝1﹣+﹣+﹣+…+﹣＝1﹣＝，由，可得•＝＝，解得n＝10．故答案为：10．【点评】本题考查数列的裂项相消求和，考查方程思想和运算能力，属于基础题．10．【考点】CF：几何概型．【解答】解：由题意正六边形木板的面积S＝a2，空白部分的面积S＝，故阴影部分的面积S＝，故满足条件的概率P＝1﹣π，故答案为：1﹣π．【点评】本题考查了几何概型问题，考查特殊图象面积的求法，是一道常规题．11．【考点】HR：余弦定理．【解答】解：∵a，b是方程x2﹣13x+40＝0的两根，∴a＝5，b＝8，或a＝8，b＝5，由余弦定理AB2＝c2＝a2+b2﹣2ab cos C＝25+64﹣2×8×5×＝49，则AB＝7，故答案为：7．【点评】本题考查了方程的解和余弦定理，属于基础题12．【考点】73：一元二次不等式及其应用．【解答】解：由题意知，不等式（m﹣x）※（m+x）＜4化为（m﹣x+1）（m+x）＜4，即m2+m﹣4＜x2﹣x；设f（x）＝x2﹣x，x∈[1，2]，则f（x）的最大值是f（2）＝4﹣2＝2；令m2+m﹣4＜2，即m2+m﹣6＜0，解得﹣3＜m＜2，∴实数m的取值范围是﹣3＜m＜2．故答案为：﹣3＜m＜2．【点评】本题考查了新定义与不等式和函数的应用问题，是中档题．13．【考点】8H：数列递推式；8K：数列与不等式的综合．【解答】解：由，可得，∴a n＝n﹣1，不等式（2λ﹣3）n2≥（2λ﹣4）a n a n+1+λ+3恒成立⇔（2n﹣1）λ+n2﹣4n﹣3≥0，令f（λ）＝（2n﹣1）λ+n2﹣4n﹣3，对任意实数λ∈[0，1]，不等式（2λ﹣3）n2≥（2λ﹣4）a n a n+1+λ+3恒成立，∵2n﹣1＞0，只需f（0）＝n2﹣4n﹣3＞0，解得n＞2+，∵n∈N+，∴n≥5，则k的最小值是5．故答案为：5．【点评】本题考查了等差数列与等比数列的通项公式、一次函数的单调性、不等式的解法，考查了推理能力与计算能力，属于中档题．14．【考点】7F：基本不等式及其应用．【解答】解：x＞0，y＞0，则+＝＝＝，可令t＝+，可得t≥2，则+＝＝，由y＝t+在t≥2递增，可得t+≥2+＝，可得≤8×＝，当且仅当x＝y时，上式取得等号，则+的最大值是，故答案为：．【点评】本题考查基本不等式的运用：求最值，考查化简变形能力，以及换元法的运用，对勾函数的单调性，考查运算求解能力，属于难题．二、解答题（本大题共6小题，共计90分．请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤．）15．【考点】B7：分布和频率分布表；BB：众数、中位数、平均数．【解答】解：（1）由频率分布表得第4组中的频数是12，频率是0.300，∴n＝＝40．数据[135，145）的频率为：1﹣（0.025+0.05+0.2+0.3+0.275+0.05）＝0.1，∴利用组中值估计平均数为：90×0.025+100×0.05+110×0.2+120×0.3+130×0.275+140×0.1+150×0.05＝122.5．（2）成绩不低于135分的同学的概率为：0.1+0.05＝0.15，∴估计该校学生能参加“数学竞赛集训队”的人数大约为：500×0.15＝75人．【点评】本题考查频率分布表的应用，考查概率的求法，考查平均数、频率分布表的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．16．【考点】HP：正弦定理；HR：余弦定理．【解答】解：（1）△ABC中，角A，B，C的对边分别是a，b，c，若．利用正弦定理：，整理得：sin（B+C）＝sin B cos C+，则：sin C cos B＝sin C sin B，由于sin C≠0，所以tan B＝，由于：0＜B＜π，解得：B＝．（2）△ABC的面积S＝，所以：，解得：ac＝20，由于a＝5，所以c＝4．则：b2＝a2+c2﹣2ac cos B，＝25+16﹣20，＝21，解得：b＝．【点评】本题考查的知识要点：三角函数关系式的恒等变变换，正弦定理和余弦定理及三角形面积公式．17．【考点】8E：数列的求和．【解答】解：（1）数列{a n}是首项为，公比为q（q≠1）的等比数列，且a1，，2a3成等差数列．则：，即：2q2﹣3q+1＝0，解得：q＝1或，由于q≠1，则：，所以：．（2）由于，则：b n＝na n＝，所以：+…+①，+…+②，①﹣②得：，解得：，则：不等式16T n+n﹣30≤0，转换为，即：，所以：2n﹣4≤1，解得n≤4．故最大整数为4．【点评】本题考查的知识要点：数列的通项公式的求法及应用，乘公比错位相减法在数列求和中的应用，主要考查学生的运算能力和转化能力，属于基础题型．18．【考点】HR：余弦定理．【解答】解：（1）在等腰△ABC中，过C作CH⊥AB于H，在Rt△ACH中，由cos∠CAB＝，得，∴AH＝40，AB＝80，∴△AEF的四边形BCEF的周长相等，∴AE+AF+EF＝CE+BC+BF+EF，∴AE+AF＝（60﹣AE）+60+（80﹣AF），∴AE+AF＝100，∵E为线段AC的三等分点，（靠近C），∴AE＝40，AF+60，在△AEF中，EF2＝AE2+AF2﹣2AE•AF•cos∠CAB＝＝200，∴EF＝＝20．∴水上观光通道EF的长度为20米．（2）由（1）知，AE+AF＝100，设AE＝x，AF＝y，在△AEF中，由余弦定理得：EF2＝x2+y2﹣2xy cos∠CAB＝x2+y2﹣＝（x+y）2﹣，∵xy≤（）2＝502，∴EF2≥（100）2﹣＝，∴EF≥，当且仅当x＝y时，取等号，∴当AE＝50米时，观光通道EF的长度最短，其最短长度为米．【点评】本题考查线段长的求法，考查余弦定理等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．19．【考点】3V：二次函数的性质与图象；73：一元二次不等式及其应用．【解答】解：（1）由题意得（m﹣1）x2+（m2+2m）x+3m2＜0，即[（m﹣1）x+3m]（x+m）＜0，当m＝1时，得x+1＜0，解得：x＜﹣1，当0＜m＜1时，得（x+）（x+m）＞0，∵﹣﹣（﹣m）＝＞0，∴﹣＞﹣m，解得：x＜﹣m，或x＞﹣，当m＞1时，得（x+）（x+m）＜0，∵﹣﹣（﹣m）＝，当m＞4时，﹣＞﹣m，解得：﹣m＜x＜﹣，当m＝4时，﹣＝﹣m，（x+4）2＜0，解集是∅，当1＜m＜4时，﹣＜﹣m，解得：﹣＜x＜﹣m，综上，0＜m＜1时，不等式解集是{x|x＜﹣m或x＞﹣}，m＝1时，不等式解集是{x|x＜﹣1}，1＜m＜4时，不等式解集是{x|﹣＜x＜﹣m}，m＝4时，不等式解集是∅，m＞4时，不等式解集是{x|﹣m＜x＜﹣}；（2）f（x）的图象是一条开口向上的抛物线，关于x＝m对称，由题意得m＞，若＜m≤1，则f（x）在[1，4m]递增，从而f（x）在[1，4m]上的最小值是f（1）＝1﹣2m﹣3m2，最大值是f（4m）＝5m2，由|f（x）|≤4m得﹣4m2≤x2﹣2mx﹣3m2≤4m，于是有，解得：，∴0＜m≤，又＜m≤1，∴＜m≤，若m＞1，此时f（4m）＝5m2＞4m，则当1≤x≤4m时，|f（x）|≤4m不恒成立，综上，使得|f（x）|≤4m，x∈[1，4m]恒成立的m的范围是（，]．【点评】本题考查了二次函数的性质，考查分类讨论思想以及转化思想，是一道综合题．20．【考点】87：等比数列的性质；8M：等差数列与等比数列的综合．【解答】解：（1）等差数列{a n}的前n项的和为S n，公差d≠0，若a4，a6，a10成等比数列，S7＝14，可得a62＝a4a10，即（a1+5d）2＝（a1+3d）（a1+9d），化为a1+d＝0，又7a1+21d＝14，解得a1＝﹣1，d＝1，则a n＝n﹣2；（2）证明：任意的n∈N*，等式b1a n+b2a n﹣1+b3a n﹣2+…+b n a1＝﹣2n都成立，可得b1a1＝﹣2，即b1＝2；由n≥2时，b1a n﹣1+b2a n﹣2+b3a n﹣3+…+b n﹣1a1＝﹣2（n﹣1），①b1a n+b2a n﹣1+b3a n﹣2+…+b n a1＝﹣2n，②两式②﹣①相减可得b1+b2+…+b n﹣1+b n a1＝﹣2，b1+b2+…+b n﹣1+b n＝﹣2+2b n，当n≥2时，b1+b2+…+b n﹣1＝﹣2+2b n﹣1，两式相减可得b n＝2b n﹣2b n﹣1，即b n＝2b n﹣1，则数列{b n}是首项和公比均为2的等比数列；（3）＝，假设存在正整数数组（s，t），使c1，c s，c t成等比数列，则lgc1，lg c s，lg c t成等差数列，于是＝+，所以t＝2t（﹣）（☆）．易知（s，t）＝（3，4）为方程（☆）的一组解．当s≥4，且s∈N*时，﹣＝＜0，故数列{}（s≥3）为递减数列，于是﹣≤﹣≤0，所以此时方程（☆）无正整数解．综上，存在唯一正整数数对（s，t）＝（3，4），c1，c s，c t成等比数列．【点评】本题考查等差数列和等比数列的通项公式和求和公式的运用，考查化简整理的运算能力，属于中档题．。

无锡市普通高中2018年春学期期终教学质量抽测建议卷高一物理2018.6制卷单位宜兴市教师发展中心命题单位宜兴市教师发展中心(本试卷满分120分，考试时间100分钟）―、单项选择题本题共8小题,每小题3分，共24分。

每小题只有一个选项符合题意。

1.在光滑绝缘的水平地面上有两个带同种电荷的小球，将两个小球由静止释放后，两小球之间的库仑力将A.不变B.变小C.变大D.无法确定2.关于开普勒对行星运动规律的认识,下列说法中正确的是A.所有行星绕太阳的运动都是匀速圆周运动B.所有行星以相同的速率绕太阳做椭圆运动C.所有行星轨道的半长轴的二次方与公转周期的三次方的比值都相同D.对于每一个行星，它在近日点时的速率均大于在远日点的速率3.在下面各实例中，机械能守恒的是A.树上飘落的树叶B.在空中匀速下降的跳伞运动员C.在空中做平抛运动的铅球D.草坪上滚动的足球4.一端固定的轻质弹簧处于原长，现用互相垂直的两个力F1、F2拉弹簧的另一端至0点，如图所示，在此过程分别做了F1、F2的功；换用另一个力F 仍使弹簧重复上述过程，则该过程中所做的功是A. 1JB.5JC.7JD.9J5.若在地面上沿水平方向直接发射一飞行器，如果发射速度大于7.9m/s，小于11.2m/s，（不计空气阻力）则它将A.围绕地球做圆周运动B.围绕地球做椭圆运动C.挣脱地球的束缚绕太阳运动D.挣脱太阳的束缚飞离太阳系6.用控制变量法，可以研究影响平行板电容器电容的因素（如图）。

设两极板正对面积为S，极板间的距离为d，静电计指针偏角为 。

实验中，极板所带电荷量不变，若A.保持S 不变，增大d ，则θ变大B.保持S 不变，增大A 则θ变小C.保持d 不变，减小S ，则θ变小D.保持d 不变，减小S ，由θ不变7.将一电荷量为+ Q 的小球放在不带电的金属球附近，所形成的电场线分布如图所示，金属球表面的电势处处相等。

a 、b 为电场中的两点，则A.a 点的电场强度比b 点的小B.a 点的电势比b 点的低C.将检验电荷-q 点移到b 点的过程中，电场力做正功D.检验电荷-q 在a 点的电势能比在b 点的小8.如图所示，质量为m 和3m 的小球A 和B 系在长为L 的光滑细线两端，桌面水平光滑，高h(h<L)，B 球无初速度从桌边滑下，落在沙地上静止不动，则A 球离开桌边的速度为A. 23gh B. gh 2 C.3gh D. 6gh 二、多项选择题本题共6小题，每小题4分，共24分。

2017-2018学年江苏省无锡市高一（下）期末数学试卷一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．）1．（5分）某校有老师200人，男学生1200人，女学生1000人，现用分层抽样的方法从所有师生中抽取一个容量为120人的样本进行某项调查，则应抽取的男学生人数为．2．（5分）等比数列{a n}中，若a2＝1，a5＝8，则a7＝．3．（5分）△ABC中，，BC＝3，，则∠C＝．4．（5分）如图，有四根木棒穿过一堵墙，两人分别站在墙的左、右两边，各选该边的一根木棒．若每边每根木棒被选中的机会相等，则两人选到同一根木棒的概率为．5．（5分）已知某人连续5次射击的环数分别是8，9，10，x，8，若这组数据的平均数是9，则这组数据的方差为．6．（5分）如图所示是一算法的伪代码，执行此算法时，输出的结果是．7．（5分）已知实数x，y满足，则z＝9x•3y的最大值是．8．（5分）在等差数列{a n}中，a n＞0，a4＝5，则的最小值为．9．（5分）设，且，则n ＝．10．（5分）如图所示，墙上挂有一块边长为a的正六边形木板，它的六个角的空白部分都是以正六边形的顶点为圆心，半径为的扇形面，某人向此板投镖一次，假设一定能击中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是．11．（5分）在△ABC中，已知∠C＝，BC＝a，AC＝b，且a，b是方程x2﹣13x+40＝0的两根，则AB的长度为．12．（5分）在R上定义运算a※b＝（a+1）b，若存在x∈[1，2]，使不等式（m﹣x）※（m+x）＜4成立，则实数m的取值范围为．13．（5分）设数列{a n}的前n项和为S n，，若对任意实数λ∈[0，1]，总存在自然数k，使得当n≥k时，不等式（2λ﹣3）n2≥（2λ﹣4）a n a n+1+λ+3恒成立，则k的最小值是．14．（5分）已知x＞0，y＞0，则+的最大值是．二、解答题（本大题共6小题，共计90分．请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤．）15．（14分）某校有500名学生参加学校组织的“数学竞赛集训队”选拔考试，现从中等可能抽出n名学生的成绩作为样本，制成如图频率分布表：（1）求n的值，并根据题中信息估计总体平均数是多少？（2）若成绩不低于135分的同学能参加“数学竞赛集训队”，试估计该校大约多少名学生能参加“数学竞赛集训队”？16．（14分）在△ABC中，角A，B，C的对边分别是a，b，c，若．（1）求角B的值；（2）若△ABC的面积S＝，a＝5，求b的值．17．（14分）已知数列{a n}是首项为，公比为q（q≠1）的等比数列，且a1，，2a3成等差数列．（1）求数列{a n}的通项公式；（2）若b n＝na n，记数列{b n}的前n项和为T n，求满足不等式16T n+n﹣30≤0的最大正整数n的值．18．（16分）如图所示，△ABC是临江公园内一个等腰三角形形状的小湖（假设湖岸是比值的），其中两腰CA＝CB＝60米，cos∠CAB＝．为了给市民营造良好的休闲环境，公园管理处决定在湖岸AC，AB上分别取点E，F（异于线段端点），在湖上修建一条笔直的水上观光通道EF（宽度不计），使得三角形AEF和四边形BCEF的周长相等．（1）若水上观光通道的端点E为线段AC的三等分点（靠近点C），求此时水上观光通道EF的长度；（2）当AE为多长时，观光通道EF的长度最短？并求出其最短长度．19．（16分）已知函数f（x）＝x2﹣2mx﹣3m2（m∈R，m＞0）．（1）解关于x的不等式f（x）＞mx2+m2x；（2）若当x∈[1，4m]时，|f（x）|≤4m恒成立，求实数m的取值范围．20．（16分）已知等差数列{a n}的前n项的和为S n，公差d≠0，若a4，a6，a10成等比数列，S7＝14，数列{b n}满足：对于任意的n∈N*，等式b1a n+b2a n﹣1+b3a n﹣2+…+b n a1＝﹣2n都成立．（1）求数列{a n}的通项公式；（2）证明：数列{b n}是等比数列；（3）若数列{c n}满足，试问是否存在正整数s，t（其中1＜s＜t），使c1，c s，c t成等比数列？若存在，求出所有满足条件的数组（s，t）；若不存在，请说明理由．2017-2018学年江苏省无锡市高一（下）期末数学试卷参考答案与试题解析一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．）1．（5分）某校有老师200人，男学生1200人，女学生1000人，现用分层抽样的方法从所有师生中抽取一个容量为120人的样本进行某项调查，则应抽取的男学生人数为60．【解答】解：分层抽样的抽取比例为：＝，∴男生中抽取的人数为1200×＝60．故答案为：60．2．（5分）等比数列{a n}中，若a2＝1，a5＝8，则a7＝32．【解答】解：等比数列{a n}中，若a2＝1，a5＝8，∴a5＝a2q3，∴q3＝8，∴q＝2，则a7＝a5q2＝8×4＝32，故答案为：323．（5分）△ABC中，，BC＝3，，则∠C＝．【解答】解：由，a＝BC＝3，c＝，根据正弦定理＝得：sin C＝＝，又C为三角形的内角，且c＜a，∴0＜∠C＜，则∠C＝．故答案为：4．（5分）如图，有四根木棒穿过一堵墙，两人分别站在墙的左、右两边，各选该边的一根木棒．若每边每根木棒被选中的机会相等，则两人选到同一根木棒的概率为．【解答】解：有四根木棒穿过一堵墙，两人分别站在墙的左、右两边，各选该边的一根木棒．基本事件总数n＝4×4＝16，每边每根木棒被选中的机会相等，两人选到同一根木棒包含的基本事件个数m＝4，∴两人选到同一根木棒的概率为p＝＝＝．故答案为：．5．（5分）已知某人连续5次射击的环数分别是8，9，10，x，8，若这组数据的平均数是9，则这组数据的方差为0.8．【解答】解：根据题意，数据8，9，10，x，8的平均数是9，则有（8+9+10+x+8）＝45，解可得：x＝10，则这组数据的方差S2＝[（8﹣9）2+（9﹣9）2+（10﹣9）2+（10﹣9）2+（8﹣9）2]＝0.8；故答案为：0.86．（5分）如图所示是一算法的伪代码，执行此算法时，输出的结果是3．【解答】解：根据题中的程序框图，可得该程序经过第一次循环，因为s＝0＜15，所以得到新的S＝0+6＝6，n＝5；然后经过第二次循环，因为s＝6＜15，所以得到新的S＝6+5＝11，n＝4；然后经过第三次循环，因为s＝11＜15，所以得到新的S＝11+4＝15，n＝3；接下来判断：因为s＝15，不满足s＜15，所以结束循环体并输出最后的n，综上所述，可得最后输出的结果是3故答案为：37．（5分）已知实数x，y满足，则z＝9x•3y的最大值是27．【解答】解：画实数x，y满足可行域如图，z为目标函数z＝9x•3y＝32x+y，u＝2x+y 的纵截距取得最大值时，z取得最大值，画直线L：0＝2x+y，平移直线过A时z有最大值，由可得A（1，1），此时u＝3，z＝27．故答案为：27．8．（5分）在等差数列{a n}中，a n＞0，a4＝5，则的最小值为 1.6．【解答】解：∵在等差数列{a n}中，a n＞0，a4＝5，∴a2+a6＝2a4＝10，∴＝（）（a2+a6）＝（++10）≥＝1.6．当且仅当＝时，取等号．故的最小值为1.6．故答案为：1.6．9．（5分）设，且，则n＝10．【解答】解：＝1﹣+﹣+﹣+…+﹣＝1﹣＝，由，可得•＝＝，解得n＝10．故答案为：10．10．（5分）如图所示，墙上挂有一块边长为a的正六边形木板，它的六个角的空白部分都是以正六边形的顶点为圆心，半径为的扇形面，某人向此板投镖一次，假设一定能击中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是1﹣π．【解答】解：由题意正六边形木板的面积S＝a2，空白部分的面积S＝，故阴影部分的面积S＝，故满足条件的概率P＝1﹣π，故答案为：1﹣π．11．（5分）在△ABC中，已知∠C＝，BC＝a，AC＝b，且a，b是方程x2﹣13x+40＝0的两根，则AB的长度为7．【解答】解：∵a，b是方程x2﹣13x+40＝0的两根，∴a＝5，b＝8，或a＝8，b＝5，由余弦定理AB2＝c2＝a2+b2﹣2ab cos C＝25+64﹣2×8×5×＝49，则AB＝7，故答案为：7．12．（5分）在R上定义运算a※b＝（a+1）b，若存在x∈[1，2]，使不等式（m﹣x）※（m+x）＜4成立，则实数m的取值范围为﹣3＜m＜2．【解答】解：由题意知，不等式（m﹣x）※（m+x）＜4化为（m﹣x+1）（m+x）＜4，即m2+m﹣4＜x2﹣x；设f（x）＝x2﹣x，x∈[1，2]，则f（x）的最大值是f（2）＝4﹣2＝2；令m2+m﹣4＜2，即m2+m﹣6＜0，解得﹣3＜m＜2，∴实数m的取值范围是﹣3＜m＜2．故答案为：﹣3＜m＜2．13．（5分）设数列{a n}的前n项和为S n，，若对任意实数λ∈[0，1]，总存在自然数k，使得当n≥k时，不等式（2λ﹣3）n2≥（2λ﹣4）a n a n+1+λ+3恒成立，则k的最小值是5．【解答】解：由，可得，∴a n＝n﹣1，不等式（2λ﹣3）n2≥（2λ﹣4）a n a n+1+λ+3恒成立⇔（2n﹣1）λ+n2﹣4n﹣3≥0，令f（λ）＝（2n﹣1）λ+n2﹣4n﹣3，对任意实数λ∈[0，1]，不等式（2λ﹣3）n2≥（2λ﹣4）a n a n+1+λ+3恒成立，∵2n﹣1＞0，只需f（0）＝n2﹣4n﹣3＞0，解得n＞2+，∵n∈N+，∴n≥5，则k的最小值是5．故答案为：5．14．（5分）已知x＞0，y＞0，则+的最大值是．【解答】解：x＞0，y＞0，则+＝＝＝，可令t＝+，可得t≥2，则+＝＝，由y＝t+在t≥2递增，可得t+≥2+＝，可得≤8×＝，当且仅当x＝y时，上式取得等号，则+的最大值是，故答案为：．二、解答题（本大题共6小题，共计90分．请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤．）15．（14分）某校有500名学生参加学校组织的“数学竞赛集训队”选拔考试，现从中等可能抽出n名学生的成绩作为样本，制成如图频率分布表：（1）求n的值，并根据题中信息估计总体平均数是多少？（2）若成绩不低于135分的同学能参加“数学竞赛集训队”，试估计该校大约多少名学生能参加“数学竞赛集训队”？【解答】解：（1）由频率分布表得第4组中的频数是12，频率是0.300，∴n＝＝40．数据[135，145）的频率为：1﹣（0.025+0.05+0.2+0.3+0.275+0.05）＝0.1，∴利用组中值估计平均数为：90×0.025+100×0.05+110×0.2+120×0.3+130×0.275+140×0.1+150×0.05＝122.5．（2）成绩不低于135分的同学的概率为：0.1+0.05＝0.15，∴估计该校学生能参加“数学竞赛集训队”的人数大约为：500×0.15＝75人．16．（14分）在△ABC中，角A，B，C的对边分别是a，b，c，若．（1）求角B的值；（2）若△ABC的面积S＝，a＝5，求b的值．【解答】解：（1）△ABC中，角A，B，C的对边分别是a，b，c，若．利用正弦定理：，整理得：sin（B+C）＝sin B cos C+，则：sin C cos B＝sin C sin B，由于sin C≠0，所以tan B＝，由于：0＜B＜π，解得：B＝．（2）△ABC的面积S＝，所以：，解得：ac＝20，由于a＝5，所以c＝4．则：b2＝a2+c2﹣2ac cos B，＝25+16﹣20，＝21，解得：b＝．17．（14分）已知数列{a n}是首项为，公比为q（q≠1）的等比数列，且a1，，2a3成等差数列．（1）求数列{a n}的通项公式；（2）若b n＝na n，记数列{b n}的前n项和为T n，求满足不等式16T n+n﹣30≤0的最大正整数n的值．【解答】解：（1）数列{a n}是首项为，公比为q（q≠1）的等比数列，且a1，，2a3成等差数列．则：，即：2q2﹣3q+1＝0，解得：q＝1或，由于q≠1，则：，所以：．（2）由于，则：b n＝na n＝，所以：+…+①，+…+②，①﹣②得：，解得：，则：不等式16T n+n﹣30≤0，转换为，即：，所以：2n﹣4≤1，解得n≤4．故最大整数为4．18．（16分）如图所示，△ABC是临江公园内一个等腰三角形形状的小湖（假设湖岸是比值的），其中两腰CA＝CB＝60米，cos∠CAB＝．为了给市民营造良好的休闲环境，公园管理处决定在湖岸AC，AB上分别取点E，F（异于线段端点），在湖上修建一条笔直的水上观光通道EF（宽度不计），使得三角形AEF和四边形BCEF的周长相等．（1）若水上观光通道的端点E为线段AC的三等分点（靠近点C），求此时水上观光通道EF的长度；（2）当AE为多长时，观光通道EF的长度最短？并求出其最短长度．【解答】解：（1）在等腰△ABC中，过C作CH⊥AB于H，在Rt△ACH中，由cos∠CAB＝，得，∴AH＝40，AB＝80，∴△AEF的四边形BCEF的周长相等，∴AE+AF+EF＝CE+BC+BF+EF，∴AE+AF＝（60﹣AE）+60+（80﹣AF），∴AE+AF＝100，∵E为线段AC的三等分点，（靠近C），∴AE＝40，AF+60，在△AEF中，EF2＝AE2+AF2﹣2AE•AF•cos∠CAB＝＝200，∴EF＝＝20．∴水上观光通道EF的长度为20米．（2）由（1）知，AE+AF＝100，设AE＝x，AF＝y，在△AEF中，由余弦定理得：EF2＝x2+y2﹣2xy cos∠CAB＝x2+y2﹣＝（x+y）2﹣，∵xy≤（）2＝502，∴EF2≥（100）2﹣＝，∴EF≥，当且仅当x＝y时，取等号，∴当AE＝50米时，观光通道EF的长度最短，其最短长度为米．19．（16分）已知函数f（x）＝x2﹣2mx﹣3m2（m∈R，m＞0）．（1）解关于x的不等式f（x）＞mx2+m2x；（2）若当x∈[1，4m]时，|f（x）|≤4m恒成立，求实数m的取值范围．【解答】解：（1）由题意得（m﹣1）x2+（m2+2m）x+3m2＜0，即[（m﹣1）x+3m]（x+m）＜0，当m＝1时，得x+1＜0，解得：x＜﹣1，当0＜m＜1时，得（x+）（x+m）＞0，∵﹣﹣（﹣m）＝＞0，∴﹣＞﹣m，解得：x＜﹣m，或x＞﹣，当m＞1时，得（x+）（x+m）＜0，∵﹣﹣（﹣m）＝，当m＞4时，﹣＞﹣m，解得：﹣m＜x＜﹣，当m＝4时，﹣＝﹣m，（x+4）2＜0，解集是∅，当1＜m＜4时，﹣＜﹣m，解得：﹣＜x＜﹣m，综上，0＜m＜1时，不等式解集是{x|x＜﹣m或x＞﹣}，m＝1时，不等式解集是{x|x＜﹣1}，1＜m＜4时，不等式解集是{x|﹣＜x＜﹣m}，m＝4时，不等式解集是∅，m＞4时，不等式解集是{x|﹣m＜x＜﹣}；（2）f（x）的图象是一条开口向上的抛物线，关于x＝m对称，由题意得m＞，若＜m≤1，则f（x）在[1，4m]递增，从而f（x）在[1，4m]上的最小值是f（1）＝1﹣2m﹣3m2，最大值是f（4m）＝5m2，由|f（x）|≤4m得﹣4m2≤x2﹣2mx﹣3m2≤4m，于是有，解得：，∴0＜m≤，又＜m≤1，∴＜m≤，若m＞1，此时f（4m）＝5m2＞4m，则当1≤x≤4m时，|f（x）|≤4m不恒成立，综上，使得|f（x）|≤4m，x∈[1，4m]恒成立的m的范围是（，]．20．（16分）已知等差数列{a n}的前n项的和为S n，公差d≠0，若a4，a6，a10成等比数列，S7＝14，数列{b n}满足：对于任意的n∈N*，等式b1a n+b2a n﹣1+b3a n﹣2+…+b n a1＝﹣2n都成立．（1）求数列{a n}的通项公式；（2）证明：数列{b n}是等比数列；（3）若数列{c n}满足，试问是否存在正整数s，t（其中1＜s＜t），使c1，c s，c t成等比数列？若存在，求出所有满足条件的数组（s，t）；若不存在，请说明理由．【解答】解：（1）等差数列{a n}的前n项的和为S n，公差d≠0，若a4，a6，a10成等比数列，S7＝14，可得a62＝a4a10，即（a1+5d）2＝（a1+3d）（a1+9d），化为a1+d＝0，又7a1+21d＝14，解得a1＝﹣1，d＝1，则a n＝n﹣2；（2）证明：任意的n∈N*，等式b1a n+b2a n﹣1+b3a n﹣2+…+b n a1＝﹣2n都成立，可得b1a1＝﹣2，即b1＝2；由n≥2时，b1a n﹣1+b2a n﹣2+b3a n﹣3+…+b n﹣1a1＝﹣2（n﹣1），①b1a n+b2a n﹣1+b3a n﹣2+…+b n a1＝﹣2n，②两式②﹣①相减可得b1+b2+…+b n﹣1+b n a1＝﹣2，b1+b2+…+b n﹣1+b n＝﹣2+2b n，当n≥2时，b1+b2+…+b n﹣1＝﹣2+2b n﹣1，两式相减可得b n＝2b n﹣2b n﹣1，即b n＝2b n﹣1，则数列{b n}是首项和公比均为2的等比数列；（3）＝，假设存在正整数数组（s，t），使c1，c s，c t成等比数列，则lgc1，lg c s，lg c t成等差数列，于是＝+，所以t＝2t（﹣）（☆）．易知（s，t）＝（3，4）为方程（☆）的一组解．当s≥4，且s∈N*时，﹣＝＜0，故数列{}（s≥3）为递减数列，于是﹣≤﹣≤0，所以此时方程（☆）无正整数解．综上，存在唯一正整数数对（s，t）＝（3，4），c1，c s，c t成等比数列．。

2017~2018学年度第二学期期末考试高一数学试卷参考公式：V柱=Sh，S为底面积，h为高．一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位．．．．．．置上．．．1. 直线的倾斜角为____．2. 在中，角所对的边分别为．已知，则的度数为____．3. 在等比数列中，公比为，为其前项和．已知，则的值为____．4. 已知正实数满足，则的最大值为____．5. 已知点在不等式组所表示的平面区域内运动，则的取值范围为____．6. 已知一个正三棱柱的侧面积为18，且侧棱长为底面边长的2倍，则该正三棱柱的体积为____．7. 在等差数列中，公差，且成等比数列，则的值为____．8. 已知，表示两条不同的直线，，表示两个不同的平面，则下列四个命题中，所有正确命题的序号为____．① 若，，则；② 若，，则；③ 若，，则；④ 若，，则．9. 在中，角所对的边分别为．已知，则的面积为____．10. 若直线与平行，则与之间的距离为____．11. 已知，，则的值为____．12. 已知数列满足，，则数列的前项和____．13. 关于的不等式的解集中恰含有3个整数，则实数的取值集合是____．14. 在中，若，则的最小值为____．二、解答题: 本大题共6小题，共计90分．请在答题卡指定的区域内作答．．．．．．．．．．．，解答时应写出文字说明、证明过程或演算步骤．15. 在中，角所对的边分别为．已知，,．（1）求的值；（2）求的值．16. 如图，在四棱锥中，为的中点．（1）若，，求证：平面；（2）若，平面平面，求证：．17. 某校一个校园景观的主题为“托起明天的太阳”，其主体是一个半径为5米的球体，需设计一个透明的支撑物将其托起，该支撑物为等边圆柱形的侧面，厚度忽略不计．轴截面如图所示，设．（注：底面直径和高相等的圆柱叫做等边圆柱．）（1）用表示圆柱的高；（2）实践表明，当球心和圆柱底面圆周上的点的距离达到最大时，景观的观赏效果最佳，求此时的值．18. 在中，边，所在直线的方程分别为，，已知是边上一点．（1）若为边上的高，求直线的方程；（2）若为边的中线，求的面积．19. 已知函数．（1）当时，解不等式；（2）若恒成立，求的取值范围．20. 已知是各项均为正数的等差数列，其前项和为，且. （1）求数列的通项公式；（2）若数列的前项和为，且，.①求证:数列是等比数列；②求满足的所有正整数的值．一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位．．．．．．置上．．．1. 直线的倾斜角为____．【答案】；【解析】即。