2015-2016年陕西省延安市黄陵中学高一(上)期中数学试卷及参考答案
- 格式:doc
- 大小:311.00 KB
- 文档页数:12

高一年级第一学期期中考试数学试卷(基础模块第一章、第二章)一、选择题(每小题5分,共60分)1.下列表示正确的是().A.{ 0 }=∅B.{全体实数}=RC.{ a }∈{a,b,c } D.{ x∈R∣x2+1=0 }=∅2.已知全集U={ 0,1,2,3,4,5},集合A={1,2,5},B={2,3,4},则(U C A)B=().A.{2}B.{0,2,3,4}C.{3,4}D.{1,2,3,4,5}3.已知A={ (x,y) | 2x-y=0 },B={ (x,y) | 3x+2y=7 },则A B=().A.{(2,1)}B.{1,2}C.{(1,2)}D.{x=1,y=2}4.设A={ x | 0< x < 1 },B={ x | x < a } ,若A⊆B,则a的取值范围是().A.[1,+∞) B.(-∞,0]C.[0,+∞)D.(-∞,1]5.已知集合A={ x | x2+14= 0 },若A∩R =∅,则实数m的取值范围是().A.m<1B.m≥1C.0<m<1D.0≤m<16.“A⊆B”是“A B=A”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.不等式21-+xx≤0的解集为().A.{ x | x≥2}B.{ x | x≥2或x<-1 }C.{ x|-1<x≤2 }D.{x| x≥2或x≤-1 }8.已知a<b<0,c>0,那么().A.a2<b2B.a b<1C.ca<cb D.ca>cb9.绝对值不等式| 2x-3 |<5的解集是().A.{ x | x<-1或x>4 }B.{ x |-1<x<4 }C.{ x | x<-1 }D.{ x | x>4 }10.与不等式-x2-2x+3>0同解的不等式(组)是().A. x2+2x-3>0B. (x+3)(x-1)<0C.x+3>0x-1D.x+3<0x-1>0⎧⎨⎩a 、b 、c 的大小顺序是( ). A.a>b>c B.c>b>a C.b>a>c D.a>c>b12.若实数0<a <1,则)0>1(a-x)(x-a的解集为( ). A.{ x |1<x<a a } B.{ x | 1<<a x a} C.{ x | 1< >x a 或x a } D.{ x | 1<a >x 或x a}二、填空题(每小题4分,共16分)13.设全集U={ 1,2,3,4,5 },A={ 2,5 },则U C A 的所有子集的个数为 _________. 14.符合条件{a}⊆M {a,c,d}的集合M的个数是 _________.15.设a,b为实数,则“a2=b2”是“a=b”的 _________条件.(填充分或必要)16.不等式2+2m x x+n>0的解集是(11,32-),则不等式2-nx +2x-m >0的解集是 _________.三、解答题(共74分,解答应写出文字说明及演算步骤) 17.已知U={ x |-2<x<7 ,x ∈N },A={ 1,2,4 },B={ 2,3,5}.求: ⑴ A U B ;⑵ A B ;⑶ B C C U U A;⑷ B C C U U A .(12分)18.若集合A={ x | mx 2+2x -1 = 0 , m ∈R , x ∈R }中有且仅有一个元素,那么m 的值是多少?(12分)19.设集合A={ x | x 2-3x +2 = 0 },B = { x | x 2+2(a +1)x +(a 2-5) = 0 },若A B = { 2 },求实数a的值.(12分) 20.解不等式x+23-x≤1.(12分) 21.设全集为R ,A={ x | |x-1|<3 },B={ x | x 2-x -2≥0 },求A B ,A U B ,A CB .(12分)22.已知集合A={ x | x 2-x -12 ≤0 },集合B={ x | m -1≤x ≤2m +3 },若A U B=A ,求实数m 的取值范围.(14分)高一年级第一学期期中考试数学试卷参考答案二、填空题(每小题4分,共16分)13、 8 14、 3 15、 必要 16、 (-2,3)三、解答题:(22题14分,17~21题每题12分,共计74分)17.解:U={ 0,1,2,3,4,5,6 }. ⑴A U B={1,2,3,4,5}.⑵A B={2}.⑶B C C U U A ={ 0,3,5,6 }U { 0,1,4,6 }={ 0,1,3,4,5,6, }. ⑷ B C C U U A={ 0,3,5,6 } { 0,1,4,6 }={ 0,6 }.18. 解:当m=0时, A=12⎧⎫⎨⎬⎩⎭,符合题意.当m ≠0时,要使集合A 中有且仅有一个元素,必须 方程mx 2+2x -1 = 0有两个相等实数根, ∴ 2∆=2+4m =0, 即m=-1,综上所述,m=0或m=-1. 19. 解:A={ 1,2 }∵ A B={ 2 }, ∴ 2 B, ∴ 2是方程x 2+2(a +1)x +(a 2-5) = 0的根,把x=2代入此方程得2a +4a+3=0, ∴ a=-1或a=-3, 当a=-1时,B={ -2,2 }, A B={ 2 },符合题意. 当a=-3时,B={ 2 }, A B={ 2 },符合题意. 综上所述,a 的值为-1或3. 20. 解:原不等式⇔x+2-13-x ≤0⇔x+2-(3-x)3-x ≤0⇔2x-13-x≤0 ⇔2x-1x-3≥00≠⎧⇔⎨⎩x-3(2x-1)(x-3)≥012⇔x ≤或x>3, ∴ 解集为12{x |x ≤或x>3}. 21. 解:解|x-1|<3得-2<x<4, 故A=(-2,4).解x 2-x -2≥0得x ≤-1或x ≥2, 故B=(-∞,-1]∪[2,+∞).∴ A B=(-2,-1]∪[2,4),A U B=R,A C B=(-2,4) (-1,2)=(-1,2).22.解: 解x2-x-12 ≤0得-3≤x≤4, 故A=[-3,4],由A U B=A,知B A,∴⎧⎪⎨⎪⎩m-1≤2m+3,m-1≥-3,2m+3≤4,即12⎧⎪⎪⎨⎪⎪⎩m≥-4,m≥-2,m≤,∴ -2≤m≤12.。

陕西省延安市黄陵中学2015-2016学年高一上学期期中考试试题注意事项:1.本试卷分第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)和答题纸三个部分,共计150分,考试时间为150分钟。
2.将答案写在答题纸上,答卷前,考生务必将自己的学校、班级、姓名、考号填写在答题纸指定处。
第I卷(选择题)本卷共8小题,每小题3分,共24分,在每小题给出的四个选项中,只有一项符合题目要求。
请将所选答案填写在答题卡上。
一、选择题,根据要求选出一个选项。
1、下列各组词语中,没有错别字的一组是()A.廖廓内涵绿草如荫逆来顺受B.和霭通揖峥嵘岁月浪遏飞舟C.殴打浸渍直冲云霄诲人不倦D.蹒跚照相陨身不恤察颜观色2、依次填入下列各句的成语,使用最恰当的一组是()(1)人生就是这样令人感慨:毕业分手的时候,大家是的青年;而今再见,大家都已华发苍颜。
(2)中国作协党组书记、副主席金炳华强调,打造一支的作家队伍是中国作协的一项重要工作。
(3)换届后的班子成员,平均年龄40岁,可谓,相信他们应该不会辜负社会各界的期望。
A.年轻有为风华正茂年富力强B.年富力强风华正茂年轻有为C.风华正茂年富力强年轻有为D.风华正茂年轻有为年富力强3、下列句子中,没有语病的一句是()A.学校能否形成良好的校园文化,学习者能否真正适应并融入其中,对教学活动的有效开展将有积极作用。
B.我们应该发挥青少年在网络文化建设中的作用,让他们成为促进网络发展的重要力量,使网络成为他们的良师益友。
C.由于青少年心智尚未成熟,容易被媒体中的不良信息诱导,从而产生思想上、行为上的偏差。
D.大观园旅游纪念品商场里摆放着名人字画、根雕作品、导游地图、古玩、佩饰等多种工艺品,琳琅满目,美不胜收。
4、下列句子组成的语段,排序最恰当的一组是()①科学家们研究了许多防热材料②在举国欢庆“东方红”的时候③提出一鼓作气载人飞天④甚至连飞船运输车和航天员吃的食品都做了出来⑤做了许多大型试验⑥中国科学家们把目光投向了更远的地方A. ②①⑤⑥③④B. ①②⑥③④⑤C. ②⑥③①⑤④D. ①③⑤④②⑥5、下列句子不是判断句的一句是()A.夫晋,何厌之有?B.亚父者,范增也C.是寡人之过也D.皆为龙虎,成五采,此天子气也。
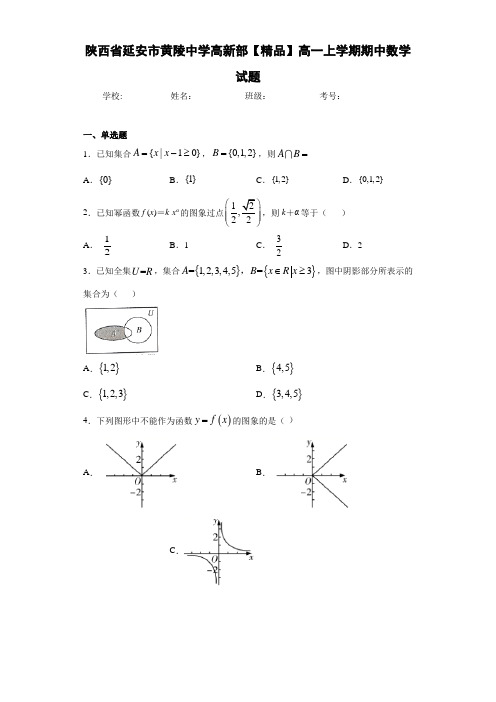
陕西省延安市黄陵中学高新部【精品】高一上学期期中数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合1}{0|A x x -≥=,{0,1,2}B =,则A B =A .{0}B .{1}C .{1,2}D .{0,1,2}2.已知幂函数f (x )=k ·x α的图象过点1,22⎛⎫⎪ ⎪⎝⎭,则k +α等于( )A .12B .1C .32D .23.已知全集=U R ,集合{}{}=1,2,3,4,5=3A B x R x ∈≥,,图中阴影部分所表示的集合为( )A .{}1,2B .{}4,5C .{}1,2,3D .{}3,4,54.下列图形中不能作为函数()y f x =的图象的是( )A .B .C .D .5.下列函数中,为偶函数的是( ) A .1y x =+B .1y x=C .4y x =D .5y x =6.下列函数中与函数y x =为同一函数的是( ) A.2y =B .2x y x=C.y = D.y =7.下列函数在()0,∞+上是增函数的是( )A .13xy ⎛⎫= ⎪⎝⎭B .25y x =-+C .ln y x =D .3y x=8.函数f(x)=ln x -22x 的零点所在的区间为( ) A .(0,1)B .(1,2)C .(2,3)D .(3,4)9.若lg lg x y a -=,则33lg lg 22x y ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭( ) A .3aB .32a C .aD .2a 10.函数xy a =与log a y x =- (0a >且1a ≠)在同一坐标系中的图象只可能是( )A .B .C .D .11.函数()245f x x x =-+在区间[]0,m 上的最大值为5,最小值为1,则实数m 的取值范围是( ) A .[)2,+∞B .[]2,4C .[]0,4D .(]2,412.设0.6 1.50.60.60.6 1.5a b c ===,,,则a b c ,,的大小关系是( )A .a b c <<B . a c b <<C .b a c <<D .b c a <<二、填空题13.设集合A ={x |-1<x <2},集合B ={x |1<x <3},则A ∪B 等于_______ 14.函数()2f x x =+的定义域为 . 15.若函数()()212g 43f x lo x x =-+,则函数()f x 的单调递减区间是__________.16.5log 3333322log 2log log 859-+-=_________________三、解答题17.已知集合{}1,2A =,{}2,3B a a =+,若{}1A B ⋂=,求实数a 的值.18.已知函数()()()221(12)22x x f x x x x x ⎧+≤-⎪=-<<⎨⎪≥⎩.()1求()4f -、()3f 、()()2f f -的值; ()2若()10f a =,求a 的值.19.已知函数()()2log 3f x x =-. (1)求()f x 的定义域;(2)若()0f x ≥,求x 的取值范围. 20.已知函数()2462f x x x =-+.(1)求()f x 的单调区间; (2)求()f x 在[]2,4上的最大值.21.二次函数()f x 满足()()12f x f x x +-=,且()01f =, (1)求()f x 的解析式;(2)在区间[11]-,上()y f x =的图象恒在2y x m =+图象的上方,试确定实数m 的范围.22.已知函数()4mf x x x=-,且()43f =. (1)求m 的值;(2)证明()f x 的奇偶性;(3)判断()f x 在()0,∞+上的单调性,并给予证明.参考答案1.C 【分析】由题意先解出集合A,进而得到结果. 【详解】解:由集合A 得x 1≥, 所以{}A B 1,2⋂= 故答案选C. 【点睛】本题主要考查交集的运算,属于基础题. 2.C 【分析】根据函数是幂函数,结合过点的坐标,即可求得,k α,则问题得解. 【详解】由幂函数的定义,知1122k k α=⎧⎛⎫=⋅ ⎪⎝⎭⎩∴k =1,α=12. ∴k +α=32.故选:C . 【点睛】本题考查根据函数是幂函数求参数值,以及待定系数法求参数值,属简单题. 3.A 【分析】由题意可知,阴影部分所表示的元素属于A ,不属于B ,结合所给的集合求解()RB A 即可确定阴影部分所表示的集合. 【详解】由已知中阴影部分在集合A 中,而不在集合B 中,故阴影部分所表示的元素属于A ,不属于B (属于B 的补集),即(){}1,2RB A ⋂=.【点睛】本题主要考查集合的表示方法,Venn 图及其应用等知识,意在考查学生的转化能力和计算求解能力. 4.B 【分析】根据函数的定义和函数图象的关系判断,函数的定义要求定义域内的任意变量x 只能有唯一的y 与x 对应,选项B 中,不满足y 值的唯一性. 【详解】根据函数的定义可知,对应定义域内的任意变量x 只能有唯一的y 与x 对应,选项B 中,当x >0时,有两个不同的y 和x 对应,所以不满足y 值的唯一性.所以B 不能作为函数图象. 故选B . 【点睛】本题主要考查函数图象的识别,利用函数的定义是解决本题的关键,注意函数的三个条件:非空数集,定义域内x 的任意性,x 对应y 值的唯一性. 5.C 【分析】利用函数的奇偶性的定义,逐项准确判定,即可求解. 【详解】由题意,函数1y x =+为非奇非偶函数,所以A 符合题意; 函数()1f x x=,满足()11()f x f x x x -==-=--,所以函数1y x =为奇函数,所以B 不符合题意;函数()4f x x =,满足()44())(f x x x f x ==-=-,所以函数4y x =是偶函数,满足题意;函数()5f x x =,满足()55()()f x x x f x -=-=-=-,所以函数5y x =为奇函数,所以D不符合题意. 故选:C. 【点睛】本题主要考查了函数奇偶性的判定,其中解答中熟记函数的奇偶性的定义和判定方法是解答的关键,着重考查了推理与论证能力,属于基础题. 6.D【分析】判断各选项中函数的定义域,并化简函数解析式,利用函数相等的概念可得出正确选项. 【详解】两个函数相等,则两个函数的定义域相同,对应法则相同,函数y x =的定义域为R , 对于A选项,函数2y =的定义域为[)0,+∞,该函数与函数y x =不相等;对于B 选项,函数2x y x=的定义域为{}0x x ≠,该函数与函数y x =不相等;对于C 选项,函数y R ,且y x ==,该函数与函数y x =不相等; 对于D选项,函数y =的定义域为R,且y x ==,该函数与函数y x =相等.故选:D. 【点睛】本题考查相等函数的判断,考查相等函数定义的理解,属于基础题. 7.C 【分析】根据函数的单调性的定义,结合初等函数的单调性,逐项判定,即可求解. 【详解】根据指数函数的性质,可得函数13xy ⎛⎫= ⎪⎝⎭在()0,∞+为单调递减函数,不符合题意;根据一次函数的性质,可得函数25y x =-+在()0,∞+为单调递减函数,不符合题意; 根据对数函数的性质,可得函数ln y x =在()0,∞+为单调递增函数,符合题意; 根据反比例函数的性质,可得函数3y x=在()0,∞+为单调递减函数,不符合题意. 故选C. 【点睛】本题主要考查了函数的单调性的判定,其中解答中熟记初等函数的图象与性质是解答的关键,着重考查了推理与论证能力,属于基础题. 8.B 【分析】先分析出f(x)=ln x -22x 在定义域(0,+∞)上是增函数,再求出f(1)=-2<0,f(2)=ln 2-12>0,根据零点定理即得解. 【详解】 易知f(x)=ln x -22x 在定义域(0,+∞)上是增函数(增函数+增函数=增函数), 又f(1)=-2<0,f(2)=ln 2-12>0. 根据零点存在性定理,可知函数f(x)=ln x -22x有唯一零点,且在区间(1,2)内. 故选B 【点睛】本题主要考查函数单调性的判断和函数的零点问题,意在考查学生对这些知识的理解掌握水平,属于基础题. 9.A 【解析】lg lg x y a -=,lg ,x a y ⎛⎫∴=∴ ⎪⎝⎭33lg lg 22x y ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭3332lg[]lg 3lg 32x x x a y y y ⎛⎫⎪⎛⎫⎛⎫⎝⎭=== ⎪ ⎪⎛⎫⎝⎭⎝⎭⎪⎝⎭,故选A. 10.C 【分析】根据指数和对数函数的性质,利用排除法即可得正确选项. 【详解】对于选项A :由xy a =单调递增,可知1a >,此时1log log a ay x x =-=在()0,∞+单调递减,故选项A 不正确;对于选项B :由x y a =单调递减,可知01a <<,此时1log log a ay x x =-=在()0,∞+单调递增,故选项B 不正确;对于选项C :由x y a =单调递增,可知1a >,此时1log log a ay x x =-=在()0,∞+单调递减,故选项C 正确;对于选项D :log a y x =-定义域为()0,∞+,故选项D 不正确; 故选:C 11.B 【分析】由函数的解析式可得函数f (x )=x 2﹣4x +5=(x ﹣2)2+1的对称轴为x =2,此时,函数取得最小值为1,当x =0或x =4时,函数值等于5,结合题意求得m 的范围. 【详解】∵函数f (x )=x 2﹣4x +5=(x ﹣2)2+1的对称轴为x =2,此时,函数取得最小值为1, 当x =0或x =4时,函数值等于5.且f (x )=x 2﹣4x +5在区间[0,m ]上的最大值为5,最小值为1, ∴实数m 的取值范围是[2,4], 故选:B . 【点睛】本题主要考查二次函数的性质应用,利用函数图像解题是关键,属于中档题. 12.C 【解析】由0.6xy =在区间(0,)+∞是单调减函数可知, 1.50.600.60.61<<<,又0.61.51>,故选C . 考点:1.指数函数的性质;2.函数值比较大小.13.{x|-1<x<3} 【解析】 【分析】根据并集的定义解答即可. 【详解】根据并集的定义知:A ∪B ={x|-1<x <3}, 即答案为{x|-1<x<3} 【点睛】本题考查了并集运算,熟练掌握并集的定义是解题的关键. 14.【解析】试题分析:要使函数有意义,需满足40{20x x +≥+≠,所以[4,2)(2,)x ∈--⋃-+∞考点:函数定义域 15.(3,)+∞ 【解析】由2430x x -+>,解得3x >或1x <,令()()243,,13,t x x x =-+∈-∞⋃+∞,∵()3,x ∈+∞时函数243t x x =-+为增函数,而12log t 为减函数,∴函数()()212log 43f x x x =-+的单调减区间为()3,+∞,故答案为()3,+∞.点睛:本题考查了与对数函数有关的复合函数的单调性,考查了对数函数值域的求法,是中档题;由对数式的真数大于0求解函数定义域,根据“同增异减”的原则,求得内函数的增区间即为复合函数的减区间; 16.1- 【分析】利用对数式的运算性质计算即可. 【详解】解:原式()33332log 2log 32log 93log 23=--+-3332log 25log 223log 23=-++-1=-,故答案为1-. 【点睛】本题考查对数式的运算性质,关键在于公式的使用,如log log na ab n b =,log a b a b =等,是基础题. 17.1 【分析】根据{}1A B ⋂=得知1B ∈,由233a +≥可得出1a =,由此得出实数a 的值. 【详解】{}1A B =,{}1,2A =,1B ∴∈且2∉B ,233a +≥,则1a =,则{}1,4B =,合乎题意.因此,1a =.【点睛】本题考查利用交集的结果求参数,在计算有限集的问题中,求出参数后还应进行检验,考查运算求解能力,属于基础题.18.(1)(4)2,(3)6,[(0)]0f f f f -=-== (2)5a =【分析】(1)根据所求值的取值范围分段代入对应解析式求解.(2)讨论a 的范围分段代入解析式求解.【详解】(1)()()4422,3236,f f -=-+=-=⨯=()2220,f -=-+=则()()200f f f ⎡⎤-==⎣⎦.(2) 1a ≤-时,()210f a a =+=,解得8a =(舍);12a -<<时,()210f a a ==,则a =; 2a ≥时,()210f a a ==,则5a =.所以a 的值为5.【点睛】分段函数分段求解,含参数求值问题要注意结合分段函数各段自变量的取值范围分类讨论求解,每一段所求结果要符合各段条件.19.(1)()3,+∞;(2)[)4,+∞.【分析】(1)由真数大于零可求出函数()y f x =的定义域;(2)由对数函数的单调性得出31x -≥,解出即可.【详解】(1)()()2log 3f x x =-,30x ∴->,解得3x >,因此,函数()y f x =的定义域为()3,+∞;(2)()()2log 30f x x =-≥,得31x -≥,解得4x ≥,因此,x 的取值范围是[)4,+∞.【点睛】本题考查对数函数定义域的求解,同时也考查了对数不等式的求解,涉及对数函数单调性的应用,考查运算求解能力,属于基础题.20.(1)减区间3,4⎛⎫-∞ ⎪⎝⎭,增区间3,4⎛⎫+∞ ⎪⎝⎭;(2)42. 【分析】(1)分析二次函数()y f x =图象的开口方向和对称轴可得出该函数的减区间和增区间; (2)分析二次函数()y f x =在区间[]2,4上的单调性,可得出函数()y f x =在区间[]2,4上的最大值.【详解】(1)二次函数()y f x =的图象开口向上,对称轴为直线34x =, 因此,函数()y f x =的单调递减区间为3,4⎛⎫-∞ ⎪⎝⎭,单调递增区间为3,4⎛⎫+∞ ⎪⎝⎭; (2)由(1)可知函数()y f x =在区间[]2,4上单调递增, ∴当4x =时,函数()y f x =取得最大值()244464242f =⨯-⨯+=.【点睛】本题考查二次函数单调区间和最值的求解,要结合二次函数图象的开口方向和对称轴来分析二次函数的单调性,考查分析问题和解决问题的能力,属于基础题.21.(1)2()1f x x x =-+ (2)1m <-【分析】(1)设2()(0)f x ax bx c a =++≠,代入()()12f x f x x +-=,()01f =待定系数即得解;(2)转换2()1y f x x x ==-+的图象恒在2y x m =+图象上方为212x x x m -+>+,令2()31g x x x m =-+-,转化为二次函数在定区间的最小值即得解.(1)由题设2()(0)f x ax bx c a =++≠∵ (0)1f =∴1c = 又(1)()2f x f x x +-=∴ 22(1)(1)()2a x b x c ax bx c x ++++-++=∴ 22ax a b x ++=∴ 220a a b =⎧⎨+=⎩ ∴ 11a b =⎧⎨=-⎩∴ 2()1f x x x =-+(2)当[1,1]x ∈-时,2()1y f x x x ==-+的图象恒在2y x m =+图象上方∴ [1,1]x ∈-时212x x x m -+>+恒成立,即2310x x m -+->恒成立令2()31g x x x m =-+-, [1,1]x ∈-时,2min ()(1)13111g x g m m ==-⨯+-=--故只要1m <-即可,实数m 的范围1m <-【点睛】本题考查了二次函数的图像和性质,考查了学生综合分析,转化划归,数学运算能力,属于中档题.22.(1)1m =;(2)奇函数,证明见解析;(3)单调增函数,证明见解析.【分析】(1)由()43f =可计算出m 的值;(2)先求出函数()y f x =的定义域,然后利用函数奇偶性的定义可证明出函数()y f x =为奇函数;(3)任取120x x >>,作差()()12f x f x -,通分并因式分解,判断()()12f x f x -的符号,即可证明出函数()y f x =在()0,∞+上单调递增.(1)()4444134m m f =-=-=,解得1m =; (2)因为()4f x x x =-,定义域为{}0x x ≠,关于原点对称, 又()()44f x x x f x x x ⎛⎫-=--=--=- ⎪-⎝⎭,因此,函数()y f x =为奇函数; (3)设120x x >>,则()()()12121212214444f x f x x x x x x x x x ⎛⎫⎛⎫-=---=-+- ⎪ ⎪⎝⎭⎝⎭()()()1212121212441x x x x x x x x x x -⎛⎫=-+=-+ ⎪⎝⎭, 因为120x x >>,所以120x x ->,所以()()12f x f x >,因此,函数()y f x =在()0,∞+上为单调增函数.【点睛】本题考查利用函数值求参数,同时也考查了利用定义证明函数的奇偶性和单调性,考查运算求解能力与推理能力,属于中等题.。

2015-2016学年陕西省延安市黄陵中学高一(上)期中数学试卷一、选择题(本题共15小题,每小题5分,共75分)1.(5.00分)集合{0,1}的子集有()个.A.1个 B.2个 C.3个 D.4个2.(5.00分)已知集合M={x|x2﹣1=0},则下列式子正确的是()A.{﹣1}∈M B.1⊊M C.﹣1∈M D.﹣1∉M3.(5.00分)已知集合M={﹣1,0,1,3,5},N={﹣2,1,2,3,5},则M∩N=()A.{﹣1,1,3}B.{1,2,5}C.{1,3,5}D.φ4.(5.00分)设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(∁u A)∪(∁u B)等于()A.{1}B.{0,1}C.{0,1,4}D.{0,1,2,3,4}5.(5.00分)若,则f(3)=()A.2 B.4 C.D.106.(5.00分)下列四个函数中,与y=x表示同一函数的是()A.y=()2B.y=C.y=D.y=7.(5.00分)若a>0,且a≠1,则函数y=log a(x+1)的图象一定过点()A.(0,0) B.(1,0) C.(﹣1,0 )D.(1,1)8.(5.00分)二次函数y=4x2﹣mx+5的对称轴为x=﹣2,则当x=1时,y的值为()A.﹣7 B.1 C.17 D.259.(5.00分)设a=22.5,b=2.50,c=,则a,b,c的大小关系是()A.a>c>b B.c>a>b C.a>b>c D.b>a>c10.(5.00分)使不等式23x﹣1﹣2>0成立的x的取值范围是()A.B.C.D.11.(5.00分)函数f(x)=3x﹣4的零点所在区间为()A.(0,1) B.(﹣1,0)C.(2,3) D.(1,2)12.(5.00分)如果函数f(x)=x2+2(a﹣1)x+2在(﹣∞,4]上是减函数,那么实数a取值范围是()A.a≤﹣3 B.a≥﹣3 C.a≤5 D.a≥513.(5.00分)已知a>1,函数y=a x与y=log a(﹣x)的图象只可能是()A.B.C.D.14.(5.00分)若f(x)=a x(a>0且a≠1)对于任意实数x、y都有()A.f(xy)=f(x)•(y)B.f(xy)=f(x)+(y)C.f(x+y)=f(x)f(y)D.f(x+y)=f(x)+f(y)15.(5.00分)下列所给4个图象中,与所给3件事吻合最好的顺序为()(1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;(2)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A.(4)(1)(2)B.(4)(2)(3)C.(4)(1)(3)D.(1)(2)(4)二、填空题(本题共5小题,每题5分,共25分)16.(5.00分)幂函数y=f(x)的图象经过点(2,8),则f(﹣3)值为.17.(5.00分)若log a2=m,log a3=n,a2m+n=.18.(5.00分)已知函数f(x)=,则f[f()]的值是.19.(5.00分)函数的值域是.20.(5.00分)函数的定义域为.三、解答题(本题共4小题,共50分,解答应写出文字说明,证明过程或演算步骤.)21.(12.00分)计算下列各式:(1);(2).22.(12.00分)已知二次函数f(x)=x2﹣4x+1.(1)当x∈[﹣2,1]时,求函数的最值;(2)当x∈[﹣2,3]时,求函数的最值.23.(12.00分)求不等式a2x﹣7>a4x﹣1(a>0,且a≠1)中x的取值范围.24.(14.00分)已知函数fx)=,若满足f(1)=(1)求实数a的值;(2)证明:f(x)为奇函数.(3)判断并证明函数f(x)的单调性.2015-2016学年陕西省延安市黄陵中学高一(上)期中数学试卷参考答案与试题解析一、选择题(本题共15小题,每小题5分,共75分)1.(5.00分)集合{0,1}的子集有()个.A.1个 B.2个 C.3个 D.4个【解答】解:根据题意,集合{0,1}的子集有{0}、{1}、{0,1}、∅,共4个,故选:D.2.(5.00分)已知集合M={x|x2﹣1=0},则下列式子正确的是()A.{﹣1}∈M B.1⊊M C.﹣1∈M D.﹣1∉M【解答】解:∵M={x|x2﹣1=0}={1,﹣1},∴1,﹣1∈M,{1}⊂M,{﹣1}⊂M,∴C正确.故选:C.3.(5.00分)已知集合M={﹣1,0,1,3,5},N={﹣2,1,2,3,5},则M∩N=()A.{﹣1,1,3}B.{1,2,5}C.{1,3,5}D.φ【解答】解:因为集合M={﹣1,0,1,3,5},N={﹣2,1,2,3,5},所以M∩N={﹣1,0,1,3,5}∩{﹣2,1,2,3,5}={1,3,5},故选:C.4.(5.00分)设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(∁u A)∪(∁u B)等于()A.{1}B.{0,1}C.{0,1,4}D.{0,1,2,3,4}【解答】解:∵U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},∴∁u A={4},∁u B={0,1},则(∁u A)∪(∁u B)={0,1,4}.故选:C.5.(5.00分)若,则f(3)=()A.2 B.4 C.D.10【解答】解:由可得,则f(3)==2,故选:A.6.(5.00分)下列四个函数中,与y=x表示同一函数的是()A.y=()2B.y=C.y=D.y=【解答】解:选项A中的函数的定义域与已知函数不同,故排除选项A;选项B中的函数与已知函数具有相同的定义域、值域和对应关系,故是同一个函数,故选项B满足条件;选项C中的函数与已知函数的值域不同,故不是同一个函数,故排除选项C;选项D中的函数与已知函数的定义域不同,故不是同一个函数,故排除选项D;故选:B.7.(5.00分)若a>0,且a≠1,则函数y=log a(x+1)的图象一定过点()A.(0,0) B.(1,0) C.(﹣1,0 )D.(1,1)【解答】解:令x+1=1,求得x=0,y=0,故函数y=log a(x+1)的图象一定过点(0,0),故选:A.8.(5.00分)二次函数y=4x2﹣mx+5的对称轴为x=﹣2,则当x=1时,y的值为()A.﹣7 B.1 C.17 D.25【解答】解:∵二次函数y=4x2﹣mx+5的对称轴为x=﹣2,∴=﹣2∴m=﹣16则二次函数y=4x2+16x+5当x=1时,y=25故选:D.9.(5.00分)设a=22.5,b=2.50,c=,则a,b,c的大小关系是()A.a>c>b B.c>a>b C.a>b>c D.b>a>c【解答】解:∵a=22.5>20=1,b=2.50=1,,∴a>b>c.故选:C.10.(5.00分)使不等式23x﹣1﹣2>0成立的x的取值范围是()A.B.C.D.【解答】解:不等式23x﹣1﹣2>0可化为23x﹣1>2∵函数y=2x在R上为增函数,故原不等式等价于3x﹣1>1解得x>故不等式23x﹣1﹣2>0成立的x的取值范围是故选:B.11.(5.00分)函数f(x)=3x﹣4的零点所在区间为()A.(0,1) B.(﹣1,0)C.(2,3) D.(1,2)【解答】解:由函数f(x)=3x﹣4可得f(1)=3﹣4=﹣1<0,f(2)=9﹣4=5>0,故有f(1)f(2)<0,根据函数零点的判定定理可得,函数f(x)=3x﹣4的零点所在区间为(1,2),故选:D.12.(5.00分)如果函数f(x)=x2+2(a﹣1)x+2在(﹣∞,4]上是减函数,那么实数a取值范围是()A.a≤﹣3 B.a≥﹣3 C.a≤5 D.a≥5【解答】解:∵f(x)=x2+2(a﹣1)x+2=(x+a﹣1)2+2﹣(a﹣1)2其对称轴为:x=1﹣a∵函数f(x)=x2+2(a﹣1)x+2在(﹣∞,4]上是减函数∴1﹣a≥4∴a≤﹣3故选:A.13.(5.00分)已知a>1,函数y=a x与y=log a(﹣x)的图象只可能是()A.B.C.D.【解答】解:已知a>1,故函数y=a x是增函数.而函数y=log a(﹣x)的定义域为(﹣∞,0),且在定义域内为减函数,故选:B.14.(5.00分)若f(x)=a x(a>0且a≠1)对于任意实数x、y都有()A.f(xy)=f(x)•(y)B.f(xy)=f(x)+(y)C.f(x+y)=f(x)f(y)D.f(x+y)=f(x)+f(y)【解答】解:∵f(x+y)=a x+y∵f(x)=a x,f(y)=a y∴f(x+y)=a x+y∴f(x+y)=f(x)f(y)故选:C.15.(5.00分)下列所给4个图象中,与所给3件事吻合最好的顺序为()(1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;(2)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A.(4)(1)(2)B.(4)(2)(3)C.(4)(1)(3)D.(1)(2)(4)【解答】解:(1)离家不久发现自己作业本忘记在家里,回到家里,这时离家的距离为0,故应先选图象(4);(2)骑着车一路以常速行驶,此时为递增的直线,在途中遇到一次交通堵塞,则这段时间与家的距离必为一定值,故应选图象(1);(3)最后加速向学校,其距离随时间的变化关系是越来越快,故应选图象(2).故答案为:(4)(1)(2),故选:A.二、填空题(本题共5小题,每题5分,共25分)16.(5.00分)幂函数y=f(x)的图象经过点(2,8),则f(﹣3)值为﹣27.【解答】解:设所求的幂函数为f(x)=x a,∵幂函数y=f(x)的图象经过点(2,8),∴f(2)=2a=8,解得a=3.∴f(x)=x3,∴f(﹣3)=(﹣3)3=﹣27.故答案为:﹣27.17.(5.00分)若log a2=m,log a3=n,a2m+n=12.【解答】解:∵log a2=m,log a3=n,∴a m=2,a n=3,∴a2m+n=(a m)2•a n=22•3=12.故答案为:12.18.(5.00分)已知函数f(x)=,则f[f()]的值是.【解答】解:,故答案为:19.(5.00分)函数的值域是[1,+∞).【解答】解:1﹣x≥0∴;∴f(x)≥1;∴f(x)的值域为[1,+∞).故答案为:[1,+∞).20.(5.00分)函数的定义域为(,1] .【解答】解:函数的定义域为:{x|},解得{x|},故答案为:(].三、解答题(本题共4小题,共50分,解答应写出文字说明,证明过程或演算步骤.)21.(12.00分)计算下列各式:(1);(2).【解答】解:(1)原式====(2)原式===22.(12.00分)已知二次函数f(x)=x2﹣4x+1.(1)当x∈[﹣2,1]时,求函数的最值;(2)当x∈[﹣2,3]时,求函数的最值.【解答】解:f(x)=x2﹣4x+1的图象是开口向上,对称轴为x=2的抛物线;(1)由于抛物线的对称轴在区间[﹣2,1]的右侧,因此函数在[﹣2,1]上单调递减,所以,当x=﹣2时,函数取得最大值f(﹣2)=13,当x=1时,函数取得最小值f(1)=﹣2(2)由于对称轴在区间[﹣2,3]内,所以,当x=2时,函数取得最小值f(2)=﹣3,当x=﹣2时,函数取到最大值f(﹣2)=13.23.(12.00分)求不等式a2x﹣7>a4x﹣1(a>0,且a≠1)中x的取值范围.【解答】解:由a2x﹣7>a4x﹣1知需要进行分类,具体情况如下:当a>1时,∵y=a x在定义域上递增,∴2x﹣7>4x﹣1,解得x<﹣3;当0<a<1时,∵y=a x在定义域上递减,∴2x﹣7<4x﹣1,解得x>﹣3;综上得,当a>1时,x的取值范围为(﹣∞,﹣3);当0<a<1时,x的取值范围为(﹣3,+∞).24.(14.00分)已知函数fx)=,若满足f(1)=(1)求实数a的值;(2)证明:f(x)为奇函数.(3)判断并证明函数f(x)的单调性.【解答】解:(1)f(1)=;∴;∴a=1;(2)证明:;该函数定义域为R,f(﹣x)=;∴f(x)为奇函数;(3),可看出x增大时,f(x)增大,∴f(x)在R上为增函数,证明如下:设x1,x2∈R,且x1<x2,则:=;∵x1<x2;∴,;∴f(x1)<f(x2);∴f(x)在R上为增函数.。


一、选择题1.(0分)[ID :11822]函数()2312x f x x -⎛⎫=- ⎪⎝⎭的零点所在的区间为( ) A .()0,1B .()1,2C .()2,3D .()3,42.(0分)[ID :11818]已知函数f (x )=23,0{log ,0x x x x ≤>那么f 1(())8f 的值为( )A .27B .127C .-27D .-1273.(0分)[ID :11809]不等式()2log 231a x x -+≤-在x ∈R 上恒成立,则实数a 的取值范围是( ) A .[)2,+∞B .(]1,2C .1,12⎡⎫⎪⎢⎣⎭D .10,2⎛⎤ ⎥⎝⎦4.(0分)[ID :11805]三个数0.32,20.3,0.32log 的大小关系为( ).A .20.30.3log 20.32<< B .0.320.3log 220.3<<C .20.30.30.3log 22<<D .20.30.30.32log 2<<5.(0分)[ID :11801]设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-≤≤⋂=Z ,则A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,, 6.(0分)[ID :11797]关于函数()sin |||sin |f x x x =+有下述四个结论:①f (x )是偶函数 ②f (x )在区间(2π,π)单调递增 ③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是 A .①②④B .②④C .①④D .①③7.(0分)[ID :11773]如图,U 为全集,M 、P 、S 是U 的三个子集,则阴影部分所表示的集合是( )A .()M P S ⋂⋂B .()M P S ⋂⋃C .()()UM P S ⋂⋂D .()()UM P S ⋂⋃8.(0分)[ID :11786]若01a b <<<,则b a , a b , log b a ,1log ab 的大小关系为( )A .1log log b a b aa b a b >>> B .1log log a bb ab a b a >>> C .1log log b a b aa ab b >>> D .1log log a b b aa b a b >>> 9.(0分)[ID :11771]函数2()ln(28)f x x x =--的单调递增区间是 A .(,2)-∞- B .(,1)-∞ C .(1,)+∞D .(4,)+∞10.(0分)[ID :11765]函数()f x 的图象如图所示,则它的解析式可能是( )A .()212xx f x -=B .()()21xf x x =-C .()ln f x x =D .()1xf x xe =-11.(0分)[ID :11744]函数3222x xx y -=+在[]6,6-的图像大致为 A . B .C .D .12.(0分)[ID :11738]已知集合{|20}A x x =-<,{|}B x x a =<,若A B A =,则实数a 的取值范围是( ) A .(,2]-∞- B .[2,)+∞C .(,2]-∞D .[2,)-+∞13.(0分)[ID :11733]设0.60.3a =,0.30.6b =,0.30.3c =,则a ,b ,c 的大小关系为( ) A .b a c <<B .a c b <<C .b c a <<D .c b a <<14.(0分)[ID :11731]已知函数21,0,()|log ,0,x x f x x x ⎧+≤⎪=⎨⎪⎩若函数()y f x a =-有四个零点1x ,2x ,3x ,4x ,且12x x <3x <4x <,则312342()x x x x x ++的取值范围是( ) A .(0,1)B .(1,0)-C .(0,1]D .[1,0)-15.(0分)[ID :11804]已知函数()f x 的定义域为R .当0x <时,3()1f x x =-;当11x -≤≤时,()()f x f x -=-;当12x >时,11()()22f x f x +=-.则(6)f =( ) A .2-B .1-C .0D .2二、填空题16.(0分)[ID :11906]1232e 2(){log (1)2x x f x x x ,,-<=-≥,则f (f (2))的值为____________.17.(0分)[ID :11903]若函数()y f x =的定义域是[0,2],则函数0.5()log (43)g x x =-的定义域是__________.18.(0分)[ID :11902]设函数()f x 是定义在R 上的偶函数,记2()()g x f x x =-,且函数()g x 在区间[0,)+∞上是增函数,则不等式2(2)(2)4f x f x x +->+的解集为_____19.(0分)[ID :11898]已知定义在实数集R 上的偶函数()f x 在区间(],0-∞上是减函数,则不等式()()1ln f f x <的解集是________.20.(0分)[ID :11890]函数f(x)为奇函数,且x>0时,f(x)x +1,则当x<0时,f(x)=________.21.(0分)[ID :11882]函数()f x =__________. 22.(0分)[ID :11859]已知函数()f x 是定义在R 上的偶函数,且当0x ≥时,2()2f x x x =-. 若关于x 的方程()0f x m -=有四个不同的实数解,则实数m 的取值范围是_____.23.(0分)[ID :11835]甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程()(1,2,3,4)i f x i =关于时间(0)x x ≥的函数关系式分别为1()21x f x =-,22()f x x =,3()f x x =,42()log (1)f x x =+,有以下结论:①当1x >时,甲走在最前面; ②当1x >时,乙走在最前面;③当01x <<时,丁走在最前面,当1x >时,丁走在最后面; ④丙不可能走在最前面,也不可能走在最后面; ⑤如果它们一直运动下去,最终走在最前面的是甲.其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分). 24.(0分)[ID :11829]若关于 x 的方程2420x x a ---= 在区间 (1, 4) 内有解,则实数 a 的取值范围是_____.25.(0分)[ID :11863]若函数()22xf x b =--有两个零点,则实数b 的取值范围是_____.三、解答题26.(0分)[ID :12026]某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益()f x 与投资额x 成正比,且投资1万元时的收益为18万元,投资股票等风险型产品的收益()g x 与投资额x 的算术平方根成正比,且投资1万元时的收益为0.5万元,(1)分别写出两种产品的收益与投资额的函数关系;(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?27.(0分)[ID :12006]已知函数()()()sin 0,0,f x A x A ωϕωϕπ=+>><,在同一周期内,当12x π=时,()f x 取得最大值4:当712x π=时,()f x 取得最小值4-. (1)求函数()f x 的解析式;(2)若,66x ππ⎡⎤∈-⎢⎥⎣⎦时,函数()()21h x f x t =+-有两个零点,求实数t 的取值范围. 28.(0分)[ID :11976]一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x (x N *∈)件.当20x ≤时,年销售总收人为(233x x -)万元;当20x >时,年销售总收人为260万元.记该工厂生产并销售这种产品所得的年利润为y 万元.(年利润=年销售总收入一年总投资)(1)求y (万元)与x (件)的函数关系式;(2)当该工厂的年产量为多少件时,所得年利润最大?最大年利润是多少?29.(0分)[ID :11954]近年来,雾霾日趋严重,雾霾的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题,某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律,每生产该型号空气净化器x (百台),其总成本为()P x (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入()Q x (万元)满足20.522,016(){224,16x x x Q x x -+≤≤=>,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:(1)求利润函数()y f x =的解析式(利润=销售收入-总成本); (2)工厂生产多少百台产品时,可使利润最多? 30.(0分)[ID :11932]设集合2{|40,}A x x x x R =+=∈,22{|2(1)10,}B x x a x a x R =+++-=∈.(1)若A B B ⋃=,求实数a 的值; (2)若AB B =,求实数a 的范围.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1.B 2.B 3.C 4.A 5.B 6.C 7.C8.D9.D10.B11.B12.B13.B14.C15.D二、填空题16.2【解析】【分析】先求f(2)再根据f(2)值所在区间求f(f(2))【详解】由题意f(2)=log3(22–1)=1故f(f(2))=f(1)=2×e1–1=2故答案为:2【点睛】本题考查分段函数17.【解析】首先要使有意义则其次∴解得综上点睛:对于抽象函数定义域的求解(1)若已知函数f(x)的定义域为ab则复合函数f(g(x))的定义域由不等式a≤g(x)≤b求出;(2)若已知函数f(g(x))18.【解析】【分析】根据题意分析可得为偶函数进而分析可得原不等式转化为结合函数的奇偶性与单调性分析可得解可得的取值范围【详解】根据题意且是定义在上的偶函数则则函数为偶函数又由为增函数且在区间上是增函数则19.【解析】由定义在实数集上的偶函数在区间上是减函数可得函数在区间上是增函数所以由不等式得即或解得或即不等式的解集是;故答案为20.【解析】当x<0时-x>0∴f(-x)=+1又f(-x)=-f(x)∴f(x)=故填21.【解析】要使函数有意义则必须解得:故函数的定义域为:点睛:常见基本初等函数定义域的基本要求(1)分式函数中分母不等于零(2)偶次根式函数的被开方式大于或等于0(3)一次函数二次函数的定义域均为R(422.【解析】【分析】若方程有四个不同的实数解则函数与直线有4个交点作出函数的图象由数形结合法分析即可得答案【详解】因为函数是定义在R上的偶函数且当时所以函数图象关于轴对称作出函数的图象:若方程有四个不同23.③④⑤【解析】试题分析:分别取特值验证命题①②;对数型函数的变化是先快后慢当x=1时甲乙丙丁四个物体又重合从而判断命题③正确;指数函数变化是先慢后快当运动的时间足够长最前面的动物一定是按照指数型函数24.-6-2)【解析】【分析】转化成f(x)=与有交点再利用二次函数的图像求解【详解】由题得令f(x)=所以所以故答案为-6-2)【点睛】本题主要考查二次方程的有解问题考查二次函数的图像和性质意在考查学25.【解析】【分析】【详解】函数有两个零点和的图象有两个交点画出和的图象如图要有两个交点那么三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.B解析:B【解析】【分析】判断函数()2 312xf x x-⎛⎫=- ⎪⎝⎭单调递增,求出f(0)=-4,f(1)=-1,f(2)=3>0,即可判断.【详解】∵函数()2312x f x x -⎛⎫=- ⎪⎝⎭单调递增,∴f(0)=-4,f (1)=-1, f (2)=7>0,根据零点的存在性定理可得出零点所在的区间是()1,2, 故选B . 【点睛】本题考查了函数的单调性,零点的存在性定理的运用,属于容易题.2.B解析:B 【解析】 【分析】利用分段函数先求f (1)8)的值,然后在求出f 1(())8f 的值. 【详解】 f=log 2=log 22-3=-3,f=f (-3)=3-3=.【点睛】本题主要考查分段函数求值以及指数函数、对数函数的基本运算,属基础题.3.C解析:C 【解析】 【分析】由()2223122-+=-+≥x x x 以及题中的条件,根据对数函数的单调性性,对a 讨论求解即可. 【详解】由()2log 231a x x -+≤-可得()21log 23log -+≤a ax x a, 当1a >时,由()2223122-+=-+≥x x x 可知2123-+≤x x a无实数解,故舍去; 当01a <<时,()2212312-+=-+≥x x x a在x ∈R 上恒成立,所以12a ≤,解得112a ≤<. 故选:C 【点睛】本题主要考查对数函数的单调性,涉及到复合函数问题,属于中档题.4.A解析:A 【解析】 【分析】利用指数函数与对数函数的单调性即可得出. 【详解】∵0<0.32<1,20.3>1,log 0.32<0, ∴20.3>0.32>log 0.32. 故选A . 【点睛】本题考查了指数函数与对数函数的单调性,属于基础题.5.B解析:B 【解析】试题分析:依题意{}{}2,1,0,1,1,0,1,2,3,M N =--=-∴{}1,0,1M N ⋂=-. 考点:集合的运算6.C解析:C 【解析】 【分析】化简函数()sin sin f x x x =+,研究它的性质从而得出正确答案. 【详解】()()()()sin sin sin sin ,f x x x x x f x f x -=-+-=+=∴为偶函数,故①正确.当2x ππ<<时,()2sin f x x =,它在区间,2π⎛⎫π ⎪⎝⎭单调递减,故②错误.当0x π≤≤时,()2sin f x x =,它有两个零点:0,π;当0x π-≤<时,()()sin sin 2sin f x x x x =--=-,它有一个零点:π-,故()f x 在[],-ππ有3个零点:0-π,,π,故③错误.当[]()2,2x k k k *∈ππ+π∈N时,()2sin f x x =;当[]()2,22x k k k *∈π+ππ+π∈N 时,()sin sin 0f x x x =-=,又()f x 为偶函数,()f x ∴的最大值为2,故④正确.综上所述,①④ 正确,故选C .【点睛】画出函数()sin sin f x x x =+的图象,由图象可得①④正确,故选C .7.C解析:C 【解析】 【分析】先根据图中的阴影部分是M∩P 的子集,但不属于集合S ,属于集合S 的补集,然后用关系式表示出来即可. 【详解】图中的阴影部分是: M∩P 的子集,不属于集合S ,属于集合S 的补集,即是C U S 的子集则阴影部分所表示的集合是(M∩P )∩(∁U S). 故选C . 【点睛】本题主要考查了Venn 图表达集合的关系及运算,同时考查了识图能力,属于基础题.8.D解析:D 【解析】因为01a b <<<,所以10a a b b a a >>>>, 因为log log 1b b a b >>,01a <<,所以11a>,1log 0a b <.综上1log log a bb aa b a b >>>;故选D. 9.D解析:D 【解析】由228x x -->0得:x ∈(−∞,−2)∪(4,+∞), 令t =228x x --,则y =ln t ,∵x ∈(−∞,−2)时,t =228x x --为减函数; x ∈(4,+∞)时,t =228x x --为增函数; y =ln t 为增函数,故函数f (x )=ln(228x x --)的单调递增区间是(4,+∞), 故选D.点睛:形如()()y f g x =的函数为()y g x =,()y f x =的复合函数,() y g x =为内层函数,()y f x =为外层函数.当内层函数()y g x =单增,外层函数()y f x =单增时,函数()()y f g x =也单增; 当内层函数()y g x =单增,外层函数()y f x =单减时,函数()()y f g x =也单减; 当内层函数()y g x =单减,外层函数()y f x =单增时,函数()()y f g x =也单减; 当内层函数()y g x =单减,外层函数()y f x =单减时,函数()()y f g x =也单增.简称为“同增异减”.10.B解析:B 【解析】 【分析】根据定义域排除C ,求出()1f 的值,可以排除D ,考虑()100f -排除A . 【详解】根据函数图象得定义域为R ,所以C 不合题意;D 选项,计算()11f e =-,不符合函数图象;对于A 选项, ()10010099992f -=⨯与函数图象不一致;B 选项符合函数图象特征.故选:B 【点睛】此题考查根据函数图象选择合适的解析式,主要利用函数性质分析,常见方法为排除法.11.B解析:B 【解析】 【分析】由分子、分母的奇偶性,易于确定函数为奇函数,由(4)f 的近似值即可得出结果. 【详解】设32()22x x x y f x -==+,则332()2()()2222x x x xx x f x f x ----==-=-++,所以()f x 是奇函数,图象关于原点成中心对称,排除选项C .又34424(4)0,22f -⨯=>+排除选项D ;36626(6)722f -⨯=≈+,排除选项A ,故选B . 【点睛】本题通过判断函数的奇偶性,缩小考察范围,通过计算特殊函数值,最后做出选择.本题较易,注重了基础知识、基本计算能力的考查.12.B解析:B【解析】由题意可得{}|2A x x =<,结合交集的定义可得实数a 的取值范围是[)2,+∞ 本题选择B 选项.13.B解析:B 【解析】 【分析】根据指数函数的单调性得出0.60.30.30.3<,而根据幂函数的单调性得出0.30.30.30.6<,从而得出a ,b ,c 的大小关系. 【详解】 解:0.3x y =在定义域上单调递减,且0.360.<,0.60.30.30.3∴<,又0.3y x∴=在定义域上单调递增,且0.360.<,0.30.30.30.6∴<, 0.60.30.30.30.30.6∴<<,a cb ∴<<故选:B . 【点睛】考查指数函数和幂函数的单调性,以及增函数和减函数的定义.14.C解析:C 【解析】作出函数函数()21,0,|log ,0,x x f x x x ⎧+≤⎪=⎨⎪⎩的图象如图所示,由图象可知,123442,1,12x x x x x +=-=<≤, ∴ ()312334422222x x x x x x x ++=-+=-+, ∵422y x =-+在412x <≤上单调递增,∴41021x <-+≤,即所求范围为(]0,1。
2015-2016学年陕西省延安市黄陵中学高一(下)期末数学试卷一.选择题(每小题5分,共12小题,总计60分)1.(5分)某单位共有老、中、青职工430人,其中有青年职工160人,中年职工180人,老年职工90人.为了解职工身体状态,现采用分层抽样的方法进行调查,若抽取的样本中有青年职工32人,则该样本中的老年职工人数为()A.9 B.18 C.27 D.362.(5分)如图是2016年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和众数依次为()A.84,84 B.84,85 C.86,84 D.84,863.(5分)对于下列表格所示五个散点,已知求得的线性回归直线方程为=0.8x ﹣155,则实数m的值为()A.8 B.8.2 C.8.4 D.8.54.(5分)如图所示的算法中,输出的S的值为()A.15 B.16 C.17 D.185.(5分)根据下列算法语句,当输入x为60时,输出y的值为()A.25 B.30 C.31 D.616.(5分)从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,那么该同学的身高超过175cm 的概率为()A.0.8 B.0.7 C.0.3 D.0.27.(5分)一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为()A.B.C.D.8.(5分)10件产品中有7件正品,3件次品,从中任取1件,则取到次品的概率是()A.B.C.D.9.(5分)已知角α的终边上一点P的坐标为(sin,cos),则sinα的值为()A.B.C.D.10.(5分)已知α为第二象限角,且,则tan(π+α)的值是()A.B.C.D.11.(5分)若函数y=sin2x的图象向左平移个单位得到y=f(x)的图象,则()A.f(x)=cos 2x B.f(x)=sin 2x C.f(x)=﹣cos 2x D.f(x)=﹣sin 2x 12.(5分)若sin(﹣α)=,则cos(+2α)等于()A.B.C.D.二.填空题(每小题5分,共6小题,总计30分)13.(5分)某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为的学生.14.(5分)从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概是.15.(5分)从2男3女共5名同学中任选2名(每名同学被选中的机会均等),这2名都是男生或都是女生的概率等于.16.(5分)执行如图的程序框图,若输出的S=,则输入的整数p的值为.17.(5分)设向量=(﹣1,2),=(m,1),如果向量+2与2﹣平行,那么•等于.18.(5分)若函数的最小正周期为π,则ω的值为.三.解答题(共4小题,每题15分,总计60分)19.(15分)一位商人有9枚银元,其中有1枚略轻的是假银元.你能用天平(无砝码)将假银元找出来吗?写出解决这一问题的算法.20.(15分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示:(Ⅰ)求图中a的值;(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);(Ⅲ)由图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).21.(15分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:(Ⅰ)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(Ⅱ)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.22.(15分)甲﹑乙两人玩一种游戏,每次有甲﹑乙两人各出1到5根手指,若和为偶数则甲赢,否则乙赢.(1)若以A表示和为6的事件,求P(A)(2)这种游戏公平吗?试说明理由.2015-2016学年陕西省延安市黄陵中学高一(下)期末数学试卷参考答案与试题解析一.选择题(每小题5分,共12小题,总计60分)1.(5分)某单位共有老、中、青职工430人,其中有青年职工160人,中年职工180人,老年职工90人.为了解职工身体状态,现采用分层抽样的方法进行调查,若抽取的样本中有青年职工32人,则该样本中的老年职工人数为()A.9 B.18 C.27 D.36【分析】由抽取的样本中青年职工的人数求得每层所抽取的比例数,进一步求的样本中的老年职工人数.【解答】解:∵在抽取的样本中有青年职工32人,∴每个个体被抽到的概率是=,由分层抽样中的比例数相等可得样本中老年职工人数为人.故选:B.2.(5分)如图是2016年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和众数依次为()A.84,84 B.84,85 C.86,84 D.84,86【分析】根据所给的茎叶图,看出七个数据,根据分数处理方法,去掉一个最高分93和一个最低分79后,把剩下的五个数字求出平均数和众数【解答】解:由茎叶图知,去掉一个最高分93和一个最低分79后,所剩数据84,84,86,84,87的中位数为84;众数为:84;故选:A.3.(5分)对于下列表格所示五个散点,已知求得的线性回归直线方程为=0.8x ﹣155,则实数m的值为()A.8 B.8.2 C.8.4 D.8.5【分析】根据回归直线经过样本数据中心点,求出y的平均数,进而可求出t值.【解答】解:由题意,=(196+197+200+203+204)=200,=(1+3+6+7+m)=,代入=0.8x﹣155,可得=0.8×200﹣155,m=8,故选:A.4.(5分)如图所示的算法中,输出的S的值为()A.15 B.16 C.17 D.18【分析】根据图中所示的算法,由a=b 可得a=5,由b=c,得b=6,c的值没有变,从而可计算出S.【解答】解:∵a=3,b=5,c=6,由a=b,得a=5,由b=c,得b=6,∴S=5+6+6=17.故选:C.5.(5分)根据下列算法语句,当输入x为60时,输出y的值为()A.25 B.30 C.31 D.61【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数y=的函数值.【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数y=的函数值.当x=60时,则y=25+0.6(60﹣50)=31,故选:C.6.(5分)从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,那么该同学的身高超过175cm 的概率为()A.0.8 B.0.7 C.0.3 D.0.2【分析】该班同学的身高共3类:(1)身高小于160cm,(2)身高在[160,175]cm,(3)身高超过175cm,由概率和为1可得结论【解答】解:由题意可得该班同学的身高共3类:(1)身高小于160cm,(2)身高在[160,175]cm,(3)身高超过175cm,他们的概率和为1,∴所求概率P=1﹣0.2﹣0.5=0.3故选:C.7.(5分)一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为()A.B.C.D.【分析】小蜜蜂的安全飞行范围为:以这个正方体的中心为中心且边长为1的正方体内.这个小正方体的体积为大正方体的体积的,故安全飞行的概率为.【解答】解:由题知小蜜蜂的安全飞行范围为:以这个正方体的中心为中心且边长为1的正方体内.这个小正方体的体积为1,大正方体的体积为27,故安全飞行的概率为p=.故选:D.8.(5分)10件产品中有7件正品,3件次品,从中任取1件,则取到次品的概率是()A.B.C.D.【分析】本题是一个等可能事件的概率,试验发生包含的事件是从10件中取1件有C101种结果,满足条件的事件是恰好有1件次品有C31种结果,得到概率即可.【解答】解:由题意知本题是一个等可能事件的概率,试验发生包含的事件是从10件中取1件有种结果,满足条件的事件是恰好有1件次品有种结果,∴取到次品的概率是=,故选:D.9.(5分)已知角α的终边上一点P的坐标为(sin,cos),则sinα的值为()A.B.C.D.【分析】由条件利用任意角的三角函数的定义,求得sinα的值.【解答】解:∵角α终边上一点P的坐标是(sin,cos),∴x=sin,y=cos,r=|OP|=1,∴sinα=cos=﹣.故选:B.10.(5分)已知α为第二象限角,且,则tan(π+α)的值是()A.B.C.D.【分析】由α为第二象限角,根据sinα的值,利用同角三角函数间的基本关系求出cosα的值,进而求出tanα的值,原式利用诱导公式化简,将tanα的值代入计算即可求出值.【解答】解:∵α为第二象限角,sinα=,∴cosα=﹣=﹣,∴tanα==﹣,则tan(π+α)=tanα=﹣.故选:D.11.(5分)若函数y=sin2x的图象向左平移个单位得到y=f(x)的图象,则()A.f(x)=cos 2x B.f(x)=sin 2x C.f(x)=﹣cos 2x D.f(x)=﹣sin 2x 【分析】把函数y=sin2x的图象向左平移个单位,只需要在函数解析式中以x+替换x,利用诱导公式化简后得答案.【解答】解:函数y=sin2x的图象向左平移个单位,得y=sin2(x+)=sin(2x+)=cos2x.故选:A.12.(5分)若sin(﹣α)=,则cos(+2α)等于()A.B.C.D.【分析】将看作整体,将化作的三角函数.【解答】解:==﹣=﹣=2﹣1=2×﹣1=.故选:A.二.填空题(每小题5分,共6小题,总计30分)13.(5分)某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为37的学生.【分析】由题设知第八组的号码数比第三组的号码数大(8﹣3)×5,由此能求出结果.【解答】解:这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,在第三组中抽得号码为12的学生,则在第八组中抽得号码为12+(8﹣3)×5=37.故答案为:37.14.(5分)从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概是.【分析】先求出所取的3个球中没有白球的概,再用1减去它,即得所取的3个球中至少有1个白球的概率.【解答】解:所有的取法共有=10种,而没有白球的取法只有一种,故所取的3个球中没有白球的概率是,故所取的3个球中至少有1个白球的概是1﹣=,故答案为.15.(5分)从2男3女共5名同学中任选2名(每名同学被选中的机会均等),这2名都是男生或都是女生的概率等于.【分析】计算从2男3女5名学生中任选2名学生和选出的2名都是男同学或都是女同学的选法种数,利用古典概型概率公式计算可得答案.【解答】解:从2男3女5名学生中任选2名学生有=10种选法;其中选出的2名都是女同学的有=3种选法,其中选出的2名都是男同学的有=1种选法,∴这2名都是男生或都是女生的概率是=,故答案为:.16.(5分)执行如图的程序框图,若输出的S=,则输入的整数p的值为5.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算满足S=+++…+=的整数p的值,并输出,结合等比数列通项公式,可得答案.【解答】解:由程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算满足S=+++…+=的整数p的值,∵+++…+=1﹣=故==故p=5故输出的整数p的值为5故答案为:517.(5分)设向量=(﹣1,2),=(m,1),如果向量+2与2﹣平行,那么•等于.【分析】利用向量的坐标运算、共线定理、数量积运算即可得出.【解答】解:向量+2=(﹣1,2)+2(m,1)=(2m﹣1,4),2﹣=2(﹣1,2)﹣(m,1)(﹣2﹣m,3),∵向量+2与2﹣平行,∴3(2m﹣1)﹣4(﹣2﹣m)=0,解得m=.∴=﹣1×+2=.故答案为:.18.(5分)若函数的最小正周期为π,则ω的值为1.【分析】利用诱导公式化简函数的表达式,化为一个角的一个三角函数的形式,然后通过周期求出ω的值.【解答】解:函数=因为它的周期是π,所以ω=1故答案为:1三.解答题(共4小题,每题15分,总计60分)19.(15分)一位商人有9枚银元,其中有1枚略轻的是假银元.你能用天平(无砝码)将假银元找出来吗?写出解决这一问题的算法.【分析】将相等个数的银元放天平上称,看天平是否平衡,一次次称找,知道找到为止.【解答】解:方法一:S1 任取2枚银元分别放在天平的两边,如果天平左右不平衡,则轻的那一边就是假银元;如果天平平衡,则进行S2.S2 取下右边的银元,然后把剩下的7枚银元依次放在右边进行称量,直到天平不平衡,偏轻的那一边就是假银元.方法二:S1 任取两枚银元分别放在天平的两端,如果天平左右不平衡,则轻的那一边是假银元;否则进行S2.S2 重复执行S1,如果前4次天平都平衡,则剩下的那一枚是假银元.方法三:S1 把9枚银元平均分成3组,每组3枚.S2 先将其中两组放在天平的两边,如果天平左右不平衡,那么假银元就在轻的那一组;如果天平左右平衡,则假银元就在未称量的那一组内.S3 取出含有假银元的那一组,从中任取2枚银元放在天平左右两边进行称量,如果天平左右不平衡,则轻的那一边是假银元;如果天平左右平衡,则未称的那一枚就是假银元.20.(15分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示:(Ⅰ)求图中a的值;(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);(Ⅲ)由图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).【分析】(Ⅰ)根据所有频率和为1建立等式,可求出a的值;(Ⅱ)甲队员进行一次射击,欲求命中环数大于7环的概率只需将大于7环的频率进行求和即可;(Ⅲ)在甲、乙两名队员中,通过频率分布情况看队员的射击成绩哪个相对集中,那就更稳定.【解答】解:(Ⅰ)由上图可得0.01+a+0.19+0.29+0.45=1,∴a=0.06;(Ⅱ)设事件A为“甲队员射击,命中环数大于7环”,它包含三个两两互斥的事件:甲队员射击,命中环数为8环,9环,10环,∴P(A)=0.29+0.45+0.01=0.75;(Ⅲ)甲队员的射击成绩更稳定.21.(15分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:(Ⅰ)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(Ⅱ)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.【分析】(I)在100名电视观众中,收看新闻的观众共有45人,从中随机抽取5名,抽样比为,进而由大于40岁的观众为27人,得到大于40岁的观众应该抽取人数.(II)抽取的5人中,年龄大于40岁的有3人,列举出所有基本事件的个数,及满足恰有1名观众的年龄为20至40岁的基本事件个数,代入古典概型概率公式,可得答案.【解答】解:(I)在100名电视观众中,收看新闻的观众共有45人,其中20至40岁的观众有18人,大于40岁的观众共有27人.故按分层抽样方法,在应在大于40岁的观众中中抽取人.…(4分)(II)抽取的5人中,年龄大于40岁的有3人,分别记作1,2,3;20岁至40岁的观众有2人,分别高为a,b,若从5人中任取2名观众记作(x,y),…(6分)则包含的总的基本事件有:(1,2),(1,3),(1,a),(1,b),(2,3),(2,a),(2,b),(3,a),(3,b),(a,b)共10个.…(8分)其中恰有1名观众的年龄为20岁至40岁包含的基本事件有:(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)共6个.…(10分)故P(“恰有1名观众的年龄为20至40岁”)=;…(12分)22.(15分)甲﹑乙两人玩一种游戏,每次有甲﹑乙两人各出1到5根手指,若和为偶数则甲赢,否则乙赢.(1)若以A表示和为6的事件,求P(A)(2)这种游戏公平吗?试说明理由.【分析】(1)由题意知本题是一个等可能事件的概率,试验发生包含的事件数为5×5,基本事件总数为25,事件A包含的基本事件数可以列举出来共5个,根据概率公式得到结果.(2)先求出甲赢的概率,由(1)知和为偶数的基本事件为13个,甲赢的概率为,乙赢的概率为,甲赢得概率比乙赢得概率要大,所以不公平.【解答】解:(1)基本事件空间与点集S={(x,y)|x∈N*,y∈N*,1≤x≤5,1≤y≤5}中的元素一一对应因为S中点的总数为5×5=25(个),∴基本事件总数为n=25.事件A包含的基本事件数共5个:(1,5)、(2,4)、(3,3)、(4,2)、(5,1),∴P(A)==.(2)这种游戏规则不公平由(1)知和为偶数的基本事件为13个,∴甲赢的概率为,乙赢的概率为,∴这种游戏规则不公平.。
2015-2016学年陕西省延安市黄陵中学高一(下)期末数学试卷一.选择题(每小题5分,共12小题,总计60分)1.(5分)某单位共有老、中、青职工430人,其中有青年职工160人,中年职工180人,老年职工90人.为了解职工身体状态,现采用分层抽样的方法进行调查,若抽取的样本中有青年职工32人,则该样本中的老年职工人数为()A.9B.18C.27D.362.(5分)如图是2016年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和众数依次为()A.84,84B.84,85C.86,84D.84,863.(5分)对于下列表格所示五个散点,已知求得的线性回归直线方程为=0.8x﹣155,则实数m的值为()A.8B.8.2C.8.4D.8.54.(5分)如图所示的算法中,输出的S的值为()A.15B.16C.17D.185.(5分)根据下列算法语句,当输入x为60时,输出y的值为()A.25B.30C.31D.616.(5分)从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,那么该同学的身高超过175cm的概率为()A.0.8B.0.7C.0.3D.0.27.(5分)一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为()A.B.C.D.8.(5分)10件产品中有7件正品,3件次品,从中任取1件,则取到次品的概率是()A.B.C.D.9.(5分)已知角α的终边上一点P的坐标为(sin,cos),则sinα的值为()A.B.C.D.10.(5分)已知α为第二象限角,且,则tan(π+α)的值是()A.B.C.D.11.(5分)若函数y=sin2x的图象向左平移个单位得到y=f(x)的图象,则()A.f(x)=cos 2x B.f(x)=sin 2xC.f(x)=﹣cos 2x D.f(x)=﹣sin 2x12.(5分)若sin(﹣α)=,则cos(+2α)等于()A.B.C.D.二.填空题(每小题5分,共6小题,总计30分)13.(5分)某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为的学生.14.(5分)从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概是.15.(5分)从2男3女共5名同学中任选2名(每名同学被选中的机会均等),这2名都是男生或都是女生的概率等于.16.(5分)执行如图的程序框图,若输出的S=,则输入的整数p的值为.17.(5分)设向量=(﹣1,2),=(m,1),如果向量+2与2﹣平行,那么•等于.18.(5分)若函数的最小正周期为π,则ω的值为.三.解答题(共4小题,每题15分,总计60分)19.(15分)一位商人有9枚银元,其中有1枚略轻的是假银元.你能用天平(无砝码)将假银元找出来吗?写出解决这一问题的算法.20.(15分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示:(Ⅰ)求图中a的值;(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);(Ⅲ)由图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).21.(15分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:(Ⅰ)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(Ⅱ)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.22.(15分)甲、乙两人玩一种游戏,每次有甲、乙两人各出1到5根手指,若和为偶数则甲赢,否则乙赢.(1)若以A表示和为6的事件,求P(A)(2)这种游戏公平吗?试说明理由.2015-2016学年陕西省延安市黄陵中学高一(下)期末数学试卷参考答案与试题解析一.选择题(每小题5分,共12小题,总计60分)1.(5分)某单位共有老、中、青职工430人,其中有青年职工160人,中年职工180人,老年职工90人.为了解职工身体状态,现采用分层抽样的方法进行调查,若抽取的样本中有青年职工32人,则该样本中的老年职工人数为()A.9B.18C.27D.36【考点】B3:分层抽样方法.【解答】解:∵在抽取的样本中有青年职工32人,∴每个个体被抽到的概率是=,由分层抽样中的比例数相等可得样本中老年职工人数为人.故选:B.2.(5分)如图是2016年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和众数依次为()A.84,84B.84,85C.86,84D.84,86【考点】BA:茎叶图.【解答】解:由茎叶图知,去掉一个最高分93和一个最低分79后,所剩数据84,84,86,84,87的中位数为84;众数为:84;故选:A.3.(5分)对于下列表格所示五个散点,已知求得的线性回归直线方程为=0.8x﹣155,则实数m的值为()A.8B.8.2C.8.4D.8.5【考点】BK:线性回归方程.【解答】解:由题意,=(196+197+200+203+204)=200,=(1+3+6+7+m)=,代入=0.8x﹣155,可得=0.8×200﹣155,m=8,故选:A.4.(5分)如图所示的算法中,输出的S的值为()A.15B.16C.17D.18【考点】EF:程序框图.【解答】解:∵a=3,b=5,c=6,由a=b,得a=5,由b=c,得b=6,∴S=5+6+6=17.故选:C.5.(5分)根据下列算法语句,当输入x为60时,输出y的值为()A.25B.30C.31D.61【考点】EA:伪代码(算法语句).【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数y=的函数值.当x=60时,则y=25+0.6(60﹣50)=31,故选:C.6.(5分)从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,那么该同学的身高超过175cm的概率为()A.0.8B.0.7C.0.3D.0.2【考点】CB:古典概型及其概率计算公式.【解答】解:由题意可得该班同学的身高共3类:(1)身高小于160cm,(2)身高在[160,175]cm,(3)身高超过175cm,他们的概率和为1,∴所求概率P=1﹣0.2﹣0.5=0.3故选:C.7.(5分)一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为()A.B.C.D.【考点】CF:几何概型.【解答】解:由题知小蜜蜂的安全飞行范围为:以这个正方体的中心为中心且边长为1的正方体内.这个小正方体的体积为1,大正方体的体积为27,故安全飞行的概率为p=.故选:D.8.(5分)10件产品中有7件正品,3件次品,从中任取1件,则取到次品的概率是()A.B.C.D.【考点】CB:古典概型及其概率计算公式.【解答】解:由题意知本题是一个等可能事件的概率,试验发生包含的事件是从10件中取1件有种结果,满足条件的事件是恰好有1件次品有种结果,∴取到次品的概率是=,故选:D.9.(5分)已知角α的终边上一点P的坐标为(sin,cos),则sinα的值为()A.B.C.D.【考点】G9:任意角的三角函数的定义.【解答】解:∵角α终边上一点P的坐标是(sin,cos),∴x=sin,y=cos,r=|OP|=1,∴sinα=cos=﹣.故选:B.10.(5分)已知α为第二象限角,且,则tan(π+α)的值是()A.B.C.D.【考点】GE:诱导公式;GG:同角三角函数间的基本关系.【解答】解:∵α为第二象限角,sinα=,∴cosα=﹣=﹣,∴tanα==﹣,则tan(π+α)=tanα=﹣.故选:D.11.(5分)若函数y=sin2x的图象向左平移个单位得到y=f(x)的图象,则()A.f(x)=cos 2x B.f(x)=sin 2xC.f(x)=﹣cos 2x D.f(x)=﹣sin 2x【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【解答】解:函数y=sin2x的图象向左平移个单位,得y=sin2(x+)=sin(2x+)=cos2x.故选:A.12.(5分)若sin(﹣α)=,则cos(+2α)等于()A.B.C.D.【考点】GP:两角和与差的三角函数;GS:二倍角的三角函数.【解答】解:==﹣=﹣=2﹣1=2×﹣1=.故选:A.二.填空题(每小题5分,共6小题,总计30分)13.(5分)某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为37的学生.【考点】B4:系统抽样方法.【解答】解:这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,在第三组中抽得号码为12的学生,则在第八组中抽得号码为12+(8﹣3)×5=37.故答案为:37.14.(5分)从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概是.【考点】CB:古典概型及其概率计算公式.【解答】解:所有的取法共有=10种,而没有白球的取法只有一种,故所取的3个球中没有白球的概率是,故所取的3个球中至少有1个白球的概是1﹣=,故答案为.15.(5分)从2男3女共5名同学中任选2名(每名同学被选中的机会均等),这2名都是男生或都是女生的概率等于.【考点】CB:古典概型及其概率计算公式.【解答】解:从2男3女5名学生中任选2名学生有=10种选法;其中选出的2名都是女同学的有=3种选法,其中选出的2名都是男同学的有=1种选法,∴这2名都是男生或都是女生的概率是=,故答案为:.16.(5分)执行如图的程序框图,若输出的S=,则输入的整数p的值为5.【考点】EF:程序框图.【解答】解:由程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算满足S=+++…+=的整数p的值,∵+++…+=1﹣=故==故p=5故输出的整数p的值为5故答案为:517.(5分)设向量=(﹣1,2),=(m,1),如果向量+2与2﹣平行,那么•等于.【考点】9O:平面向量数量积的性质及其运算.【解答】解:向量+2=(﹣1,2)+2(m,1)=(2m﹣1,4),2﹣=2(﹣1,2)﹣(m,1)(﹣2﹣m,3),∵向量+2与2﹣平行,∴3(2m﹣1)﹣4(﹣2﹣m)=0,解得m=.∴=﹣1×+2=.故答案为:.18.(5分)若函数的最小正周期为π,则ω的值为1.【考点】H1:三角函数的周期性.【解答】解:函数=因为它的周期是π,所以ω=1故答案为:1三.解答题(共4小题,每题15分,总计60分)19.(15分)一位商人有9枚银元,其中有1枚略轻的是假银元.你能用天平(无砝码)将假银元找出来吗?写出解决这一问题的算法.【考点】E1:算法及其特点.【解答】解:方法一:S1 任取2枚银元分别放在天平的两边,如果天平左右不平衡,则轻的那一边就是假银元;如果天平平衡,则进行S2.S2 取下右边的银元,然后把剩下的7枚银元依次放在右边进行称量,直到天平不平衡,偏轻的那一边就是假银元.方法二:S1 任取两枚银元分别放在天平的两端,如果天平左右不平衡,则轻的那一边是假银元;否则进行S2.S2 重复执行S1,如果前4次天平都平衡,则剩下的那一枚是假银元.方法三:S1 把9枚银元平均分成3组,每组3枚.S2 先将其中两组放在天平的两边,如果天平左右不平衡,那么假银元就在轻的那一组;如果天平左右平衡,则假银元就在未称量的那一组内.S3 取出含有假银元的那一组,从中任取2枚银元放在天平左右两边进行称量,如果天平左右不平衡,则轻的那一边是假银元;如果天平左右平衡,则未称的那一枚就是假银元.20.(15分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示:(Ⅰ)求图中a的值;(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);(Ⅲ)由图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).【考点】B8:频率分布直方图;BC:极差、方差与标准差.【解答】解:(Ⅰ)由上图可得0.01+a+0.19+0.29+0.45=1,∴a=0.06;(Ⅱ)设事件A为“甲队员射击,命中环数大于7环”,它包含三个两两互斥的事件:甲队员射击,命中环数为8环,9环,10环,∴P(A)=0.29+0.45+0.01=0.75;(Ⅲ)甲队员的射击成绩更稳定.21.(15分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:(Ⅰ)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(Ⅱ)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.【考点】B3:分层抽样方法;CB:古典概型及其概率计算公式.【解答】解:(I)在100名电视观众中,收看新闻的观众共有45人,其中20至40岁的观众有18人,大于40岁的观众共有27人.故按分层抽样方法,在应在大于40岁的观众中中抽取人.…(4分)(II)抽取的5人中,年龄大于40岁的有3人,分别记作1,2,3;20岁至40岁的观众有2人,分别高为a,b,若从5人中任取2名观众记作(x,y),…(6分)则包含的总的基本事件有:(1,2),(1,3),(1,a),(1,b),(2,3),(2,a),(2,b),(3,a),(3,b),(a,b)共10个.…(8分)其中恰有1名观众的年龄为20岁至40岁包含的基本事件有:(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)共6个.…(10分)故P(“恰有1名观众的年龄为20至40岁”)=;…(12分)22.(15分)甲、乙两人玩一种游戏,每次有甲、乙两人各出1到5根手指,若和为偶数则甲赢,否则乙赢.(1)若以A表示和为6的事件,求P(A)(2)这种游戏公平吗?试说明理由.【考点】C8:相互独立事件和相互独立事件的概率乘法公式.【解答】解:(1)基本事件空间与点集S={(x,y)|x∈N*,y∈N*,1≤x≤5,1≤y≤5}中的元素一一对应因为S中点的总数为5×5=25(个),∴基本事件总数为n=25.事件A包含的基本事件数共5个:(1,5)、(2,4)、(3,3)、(4,2)、(5,1),∴P(A)==.(2)这种游戏规则不公平由(1)知和为偶数的基本事件为13个,∴甲赢的概率为,乙赢的概率为,∴这种游戏规则不公平.。
XXX2015-2016学年高一数学上学期期中考试试卷XXX2015-2016学年高一上学期期中考试数学试卷分为两卷,卷(Ⅰ)100分,卷(Ⅱ)50分,满分共计150分。
考试时间为120分钟。
卷(Ⅰ)一、选择题:本大题共10小题,每小题5分,共50分。
1.如果A={x|x>−1},那么正确的结论是A.A⊆B。
{0}∈A C。
{0}∈C2.函数f(x)=2−2x,则f(1)=A。
0 B.−2 C.2/2 D.−2/23.设全集I={x|x∈Z−3<x<3},A={1,2},B={−2,−1,2},则A∪(I∩B)等于A。
{1} B。
{1,2} C。
{2} D。
{0,1,2}4.与函数y=10lg(x−1)的定义域相同的函数是A。
y=x−1 B。
y=x−1 C。
y=1/(x−1) D。
y=x−15.若函数f(x)=3+3x−x与g(x)=3−3^(−x)的定义域均为R,则A。
f(x)与g(x)均为偶函数 B。
f(x)为偶函数,g (x)为奇函数C。
f(x)与g(x)均为奇函数 D。
f(x)为奇函数,g (x)为偶函数6.设a=log_3(2),b=ln2,c=5,则A。
a<b<XXX<c<a C。
c<a<b D。
c<b<a7.设函数y=x和y=1/2,则y的交点为(x,y),则x所在的区间是A.(,1)B.(1,2)C.(2,3)D.(3,4)8.已知函数f(x)是R上的偶函数,当x≥1时f(x)=x−1,则f(x)<0的解集是A.(−1,∞)B.(−∞,1)C.(−1,1)D.(−∞,−1)∪(1,∞)9.某商店同时卖出两套西服,售价均为168元,以成本计算,一套盈利20%,另一套亏损20%,此时商店A.不亏不盈B.盈利37.2元C.盈利14元D.亏损14元10.设函数f(x)在R上是减函数,则A。
f(a)>f(2a)B。
陕西省黄陵中学2016-2017学年高一数学上学期第四次月考试题(普通班)一、选择题(本大题共12小题每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在相应答题卡内) 1. 集合{}{}1,43-<=≤≤-=x x B x x A ,则IA ()=BC R ( )A.{}1->x x {}1-≥=x x B C.{}41≤<-x x D.{}41≤≤-x x 2. 集合{}{}Z x x x B R x x x x A ∈<<-=∈=--=,42,,0322,则满足条件A C⊆B 的集合C 的个数是( )A.5B.6C.7D.83.下列各组函数中,表示同一个函数的是( )A.1-=x y 和112+-=x x y B.0x y =和1=yC.()2xx f =和()()21+=x x g D.()()xx x f 2=和()()2x xx g =4.映射B A f →:,在f 的作用下,A 中的元素()y x ,与B 中的元素()y x --3,1对应,则B 中的元素()1,0对应A 中的元素是( )A. ()2,1-B. ()3,0C.()2,1D. ()3,1-5.已知()()()⎪⎩⎪⎨⎧≤>=030log 41x x x x f x,那么()[]2f f 等于( ) A.3 B.33 C.3 D.31 6.已知函数()x x x f +-=12,则()x f 的值域是( )A.⎪⎭⎫⎢⎣⎡+∞,21B.⎥⎦⎤ ⎝⎛-∞-21, C.()+∞,0 D.[)+∞,17.设)0(2)(log 2>=x x f x,则)3(f 的值是( ) A.128 B.256 C.512 D.88. 若函数()x f y =是函数)1,0(≠>=a a a y x的反函数,且21)2(=f 则=)(x f ( ) A.x 2log B.x 21C.x 21log D.22-x 9.下列函数中,是偶函数,且在区间()+∞,0上单调递减的是( )A.x y ⎪⎭⎫ ⎝⎛=32B.32x y = C. 32-=x y D.x y 32log -=10.已知双曲线C :116922=-y x 的左右焦点分别为21,F F ,P 为C 的右支上一点,且21253F F PF =,则21F PF ∆的面积等于( ) A. 8 B. 78 C. 148 D. 1611.已知函数x x x f sin 2)(+=,且0)14()32(22≤+-++-x x f y y f ,则当1≥y 时,1+x y的取值范围是( )A .⎥⎦⎤⎢⎣⎡43,41B .⎥⎦⎤⎢⎣⎡43,0 C .⎥⎦⎤⎢⎣⎡21,41 D .⎥⎦⎤⎢⎣⎡31,4112.已知函数⎩⎨⎧>-≤⋅=0,ln 0,)(x x x e a x f x ,其中e 为自然对数的底数,若关于x 的方程0))((=x f f 有且只有一个实数解,则实数a 的取值范围为( )A .)0,(-∞B .),1()1,0(+∞YC .)1,0(D . )1,0()0,(Y -∞二、填空题(本大题共4小题,每小题5分,共20分)13.已知集合{}{}12,1,3,3,1,22-+-=-+=a a a B a a A ,且{}3-=B A I ,则=B A Y .14.设5123⎪⎭⎫ ⎝⎛=a ,5135⎪⎭⎫ ⎝⎛=b ,3135⎪⎭⎫⎝⎛=c ,35log 2=d ,则d c b a ,,,从小到大关系是 . 15.若函数())3(log 25.0a ax x x f +-=在[)+∞,2上是减少的,则a 的取值范围是 .16.若二次函数462--=x x y 在区间[]n m ,上的值域为[]4,13--,则m n -的范围是 .三、解答题(本大题共6小题,共70分)17.(10分) 已知()x f 是定义在R 上的偶函数,且当0≤x 时,)13(log )(41+-=x x f(1)求:)0(f ,)1(f ; (2)求函数()x f 的解析式;(3)若3)1(-<-a f ,求实数a 的取值范围。
2015-2016学年陕西省延安市黄陵中学高一(上)期中数学试卷一、选择题(本题共15小题,每小题5分,共75分)1.(5.00分)集合{0,1}的子集有()个.A.1个 B.2个 C.3个 D.4个2.(5.00分)已知集合M={x|x2﹣1=0},则下列式子正确的是()A.{﹣1}∈M B.1⊊M C.﹣1∈M D.﹣1∉M3.(5.00分)已知集合M={﹣1,0,1,3,5},N={﹣2,1,2,3,5},则M∩N=()A.{﹣1,1,3}B.{1,2,5}C.{1,3,5}D.φ4.(5.00分)设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(∁u A)∪(∁u B)等于()A.{1}B.{0,1}C.{0,1,4}D.{0,1,2,3,4}5.(5.00分)若,则f(3)=()A.2 B.4 C.D.106.(5.00分)下列四个函数中,与y=x表示同一函数的是()A.y=()2B.y=C.y=D.y=7.(5.00分)若a>0,且a≠1,则函数y=log a(x+1)的图象一定过点()A.(0,0) B.(1,0) C.(﹣1,0 )D.(1,1)8.(5.00分)二次函数y=4x2﹣mx+5的对称轴为x=﹣2,则当x=1时,y的值为()A.﹣7 B.1 C.17 D.259.(5.00分)设a=22.5,b=2.50,c=,则a,b,c的大小关系是()A.a>c>b B.c>a>b C.a>b>c D.b>a>c10.(5.00分)使不等式23x﹣1﹣2>0成立的x的取值范围是()A.B.C.D.11.(5.00分)函数f(x)=3x﹣4的零点所在区间为()A.(0,1) B.(﹣1,0)C.(2,3) D.(1,2)12.(5.00分)如果函数f(x)=x2+2(a﹣1)x+2在(﹣∞,4]上是减函数,那么实数a取值范围是()A.a≤﹣3 B.a≥﹣3 C.a≤5 D.a≥513.(5.00分)已知a>1,函数y=a x与y=log a(﹣x)的图象只可能是()A.B.C.D.14.(5.00分)若f(x)=a x(a>0且a≠1)对于任意实数x、y都有()A.f(xy)=f(x)•(y)B.f(xy)=f(x)+(y)C.f(x+y)=f(x)f(y)D.f(x+y)=f(x)+f(y)15.(5.00分)下列所给4个图象中,与所给3件事吻合最好的顺序为()(1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;(2)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A.(4)(1)(2)B.(4)(2)(3)C.(4)(1)(3)D.(1)(2)(4)二、填空题(本题共5小题,每题5分,共25分)16.(5.00分)幂函数y=f(x)的图象经过点(2,8),则f(﹣3)值为.17.(5.00分)若log a2=m,log a3=n,a2m+n=.18.(5.00分)已知函数f(x)=,则f[f()]的值是.19.(5.00分)函数的值域是.20.(5.00分)函数的定义域为.三、解答题(本题共4小题,共50分,解答应写出文字说明,证明过程或演算步骤.)21.(12.00分)计算下列各式:(1);(2).22.(12.00分)已知二次函数f(x)=x2﹣4x+1.(1)当x∈[﹣2,1]时,求函数的最值;(2)当x∈[﹣2,3]时,求函数的最值.23.(12.00分)求不等式a2x﹣7>a4x﹣1(a>0,且a≠1)中x的取值范围.24.(14.00分)已知函数fx)=,若满足f(1)=(1)求实数a的值;(2)证明:f(x)为奇函数.(3)判断并证明函数f(x)的单调性.2015-2016学年陕西省延安市黄陵中学高一(上)期中数学试卷参考答案与试题解析一、选择题(本题共15小题,每小题5分,共75分)1.(5.00分)集合{0,1}的子集有()个.A.1个 B.2个 C.3个 D.4个【解答】解:根据题意,集合{0,1}的子集有{0}、{1}、{0,1}、∅,共4个,故选:D.2.(5.00分)已知集合M={x|x2﹣1=0},则下列式子正确的是()A.{﹣1}∈M B.1⊊M C.﹣1∈M D.﹣1∉M【解答】解:∵M={x|x2﹣1=0}={1,﹣1},∴1,﹣1∈M,{1}⊂M,{﹣1}⊂M,∴C正确.故选:C.3.(5.00分)已知集合M={﹣1,0,1,3,5},N={﹣2,1,2,3,5},则M∩N=()A.{﹣1,1,3}B.{1,2,5}C.{1,3,5}D.φ【解答】解:因为集合M={﹣1,0,1,3,5},N={﹣2,1,2,3,5},所以M∩N={﹣1,0,1,3,5}∩{﹣2,1,2,3,5}={1,3,5},故选:C.4.(5.00分)设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(∁u A)∪(∁u B)等于()A.{1}B.{0,1}C.{0,1,4}D.{0,1,2,3,4}【解答】解:∵U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},∴∁u A={4},∁u B={0,1},则(∁u A)∪(∁u B)={0,1,4}.故选:C.5.(5.00分)若,则f(3)=()A.2 B.4 C.D.10【解答】解:由可得,则f(3)==2,故选:A.6.(5.00分)下列四个函数中,与y=x表示同一函数的是()A.y=()2B.y=C.y=D.y=【解答】解:选项A中的函数的定义域与已知函数不同,故排除选项A;选项B中的函数与已知函数具有相同的定义域、值域和对应关系,故是同一个函数,故选项B满足条件;选项C中的函数与已知函数的值域不同,故不是同一个函数,故排除选项C;选项D中的函数与已知函数的定义域不同,故不是同一个函数,故排除选项D;故选:B.7.(5.00分)若a>0,且a≠1,则函数y=log a(x+1)的图象一定过点()A.(0,0) B.(1,0) C.(﹣1,0 )D.(1,1)【解答】解:令x+1=1,求得x=0,y=0,故函数y=log a(x+1)的图象一定过点(0,0),故选:A.8.(5.00分)二次函数y=4x2﹣mx+5的对称轴为x=﹣2,则当x=1时,y的值为()A.﹣7 B.1 C.17 D.25【解答】解:∵二次函数y=4x2﹣mx+5的对称轴为x=﹣2,∴=﹣2∴m=﹣16则二次函数y=4x2+16x+5当x=1时,y=25故选:D.9.(5.00分)设a=22.5,b=2.50,c=,则a,b,c的大小关系是()A.a>c>b B.c>a>b C.a>b>c D.b>a>c【解答】解:∵a=22.5>20=1,b=2.50=1,,∴a>b>c.故选:C.10.(5.00分)使不等式23x﹣1﹣2>0成立的x的取值范围是()A.B.C.D.【解答】解:不等式23x﹣1﹣2>0可化为23x﹣1>2∵函数y=2x在R上为增函数,故原不等式等价于3x﹣1>1解得x>故不等式23x﹣1﹣2>0成立的x的取值范围是故选:B.11.(5.00分)函数f(x)=3x﹣4的零点所在区间为()A.(0,1) B.(﹣1,0)C.(2,3) D.(1,2)【解答】解:由函数f(x)=3x﹣4可得f(1)=3﹣4=﹣1<0,f(2)=9﹣4=5>0,故有f(1)f(2)<0,根据函数零点的判定定理可得,函数f(x)=3x﹣4的零点所在区间为(1,2),故选:D.12.(5.00分)如果函数f(x)=x2+2(a﹣1)x+2在(﹣∞,4]上是减函数,那么实数a取值范围是()A.a≤﹣3 B.a≥﹣3 C.a≤5 D.a≥5【解答】解:∵f(x)=x2+2(a﹣1)x+2=(x+a﹣1)2+2﹣(a﹣1)2其对称轴为:x=1﹣a∵函数f(x)=x2+2(a﹣1)x+2在(﹣∞,4]上是减函数∴1﹣a≥4∴a≤﹣3故选:A.13.(5.00分)已知a>1,函数y=a x与y=log a(﹣x)的图象只可能是()A.B.C.D.【解答】解:已知a>1,故函数y=a x是增函数.而函数y=log a(﹣x)的定义域为(﹣∞,0),且在定义域内为减函数,故选:B.14.(5.00分)若f(x)=a x(a>0且a≠1)对于任意实数x、y都有()A.f(xy)=f(x)•(y)B.f(xy)=f(x)+(y)C.f(x+y)=f(x)f(y)D.f(x+y)=f(x)+f(y)【解答】解:∵f(x+y)=a x+y∵f(x)=a x,f(y)=a y∴f(x+y)=a x+y∴f(x+y)=f(x)f(y)故选:C.15.(5.00分)下列所给4个图象中,与所给3件事吻合最好的顺序为()(1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;(2)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A.(4)(1)(2)B.(4)(2)(3)C.(4)(1)(3)D.(1)(2)(4)【解答】解:(1)离家不久发现自己作业本忘记在家里,回到家里,这时离家的距离为0,故应先选图象(4);(2)骑着车一路以常速行驶,此时为递增的直线,在途中遇到一次交通堵塞,则这段时间与家的距离必为一定值,故应选图象(1);(3)最后加速向学校,其距离随时间的变化关系是越来越快,故应选图象(2).故答案为:(4)(1)(2),故选:A.二、填空题(本题共5小题,每题5分,共25分)16.(5.00分)幂函数y=f(x)的图象经过点(2,8),则f(﹣3)值为﹣27.【解答】解:设所求的幂函数为f(x)=x a,∵幂函数y=f(x)的图象经过点(2,8),∴f(2)=2a=8,解得a=3.∴f(x)=x3,∴f(﹣3)=(﹣3)3=﹣27.故答案为:﹣27.17.(5.00分)若log a2=m,log a3=n,a2m+n=12.【解答】解:∵log a2=m,log a3=n,∴a m=2,a n=3,∴a2m+n=(a m)2•a n=22•3=12.故答案为:12.18.(5.00分)已知函数f(x)=,则f[f()]的值是.【解答】解:,故答案为:19.(5.00分)函数的值域是[1,+∞).【解答】解:1﹣x≥0∴;∴f(x)≥1;∴f(x)的值域为[1,+∞).故答案为:[1,+∞).20.(5.00分)函数的定义域为(,1] .【解答】解:函数的定义域为:{x|},解得{x|},故答案为:(].三、解答题(本题共4小题,共50分,解答应写出文字说明,证明过程或演算步骤.)21.(12.00分)计算下列各式:(1);(2).【解答】解:(1)原式====(2)原式===22.(12.00分)已知二次函数f(x)=x2﹣4x+1.(1)当x∈[﹣2,1]时,求函数的最值;(2)当x∈[﹣2,3]时,求函数的最值.【解答】解:f(x)=x2﹣4x+1的图象是开口向上,对称轴为x=2的抛物线;(1)由于抛物线的对称轴在区间[﹣2,1]的右侧,因此函数在[﹣2,1]上单调递减,所以,当x=﹣2时,函数取得最大值f(﹣2)=13,当x=1时,函数取得最小值f(1)=﹣2(2)由于对称轴在区间[﹣2,3]内,所以,当x=2时,函数取得最小值f(2)=﹣3,当x=﹣2时,函数取到最大值f(﹣2)=13.23.(12.00分)求不等式a2x﹣7>a4x﹣1(a>0,且a≠1)中x的取值范围.【解答】解:由a2x﹣7>a4x﹣1知需要进行分类,具体情况如下:当a>1时,∵y=a x在定义域上递增,∴2x﹣7>4x﹣1,解得x<﹣3;当0<a<1时,∵y=a x在定义域上递减,∴2x﹣7<4x﹣1,解得x>﹣3;综上得,当a>1时,x的取值范围为(﹣∞,﹣3);当0<a<1时,x的取值范围为(﹣3,+∞).24.(14.00分)已知函数fx)=,若满足f(1)=(1)求实数a的值;(2)证明:f(x)为奇函数.(3)判断并证明函数f(x)的单调性.【解答】解:(1)f(1)=;∴;∴a=1;(2)证明:;该函数定义域为R,f(﹣x)=;∴f(x)为奇函数;(3),可看出x增大时,f(x)增大,∴f(x)在R上为增函数,证明如下:设x1,x2∈R,且x1<x2,则:=;∵x1<x2;∴,;∴f(x1)<f(x2);∴f(x)在R上为增函数.。