当前位置：文档之家 › 《信息光学》第七章 光学全息要点

《信息光学》第七章 光学全息要点

  • 格式：ppt
  • 大小：1.02 MB
  • 文档页数：53

下载文档原格式

  / 53

合集下载

《信息光学》第七章-光学全息解析

《信息光学》第七章-光学全息解析
记录介质
5、几种不同类型的全息图
5.2 振幅全息图和位相全息图
平面全息图的复振幅透过率一般是复函数，它描述照明光波通过全息图 传播时振幅和位相所受到的调制，可以表示为
t x, y t0 x, y exp j x, y
1、引言
✓什么是全息术？
全息术（holography）是利用光的干涉和衍射原理， 将携带物质信息的光波以干涉图的形式记录下来， 并且在一定的条件下使其再现，形成原物体逼真的 立体象。由于记录了物体的全部信息，包括振幅和 相位因此称为全息术。
1、引言
✓全息发展简史
➢ 1948年 Dennis Gabor 提出 “波前重现” 理论
频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加， 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
4、基元全息图分析
如右图，参考波是由坐标在 xr , yr , zr
的点源发出的球面波，在傍轴近似下， 投射到照相胶片上的波前为：
U
x,
y
r0
exp
j
1zr
1、引言
✓全息发展பைடு நூலகம்四个阶段
第一阶段 汞灯作光源，同轴全息图
—— 萌芽阶段 第一代全息
第二阶段 激光记录，激光再现，离轴全息图
——第二代全息*
第三阶段 激光记录，白光再现
——第三代全息*
第四阶段 白光记录，白光再现
——第四代全息
1、引言
✓全息图的基本类型
1.同轴全息图 2.离轴全息图 3.菲涅耳全息图 4.傅里叶变换全息图 5.像全息图 6.模压全息 7.位相全息 8.彩虹全息图 9.体积全息图 10.计算全息
➢ 若采用参考光波照射全息图，即C(x,y)=R(x,y)，则

光学第七章光全息术小结

光学第七章光全息术小结

T~2
O~
AR'
~ ARO
物光波前真实再现
T~3O~* AR' ARei2R O~* 共轭波受到一等效棱镜
的作用，发生偏转。
典型情况三：
照明光和参考光是全同球面光。 可以设：
' R
R
二次相因子
于是：
T~2 AR' AR 常数
T3 AR' ARei2R --等效透镜
T2 O AR' ARO
可以设：
' R
R
0
于是 T~2 T~3 AR' AR 常数
T~2 O~ AR' ARO~ 物光波前再现 T~3O~* AR' ARO~* 物光共轭波前伴生
典型情况二：
照明光和参考光是斜入射的 全同平面光。
可以设：
' R
R
线性相因子
于是：
T~2 AR' AR 常数

T~3 AR' ARei2R --等效棱镜
T~2 O~ AR' ARei2R O~ 物光波前受到一等效透镜的
作用，发生放大、缩小和偏
T~3 O~* AR' ARO~*
转，也可能虚象变成实象。 伴生实象
一般性结论：
U~H' (x, y) ~tH (x, y) R~' T~1 R~'T~2 O~ T~3 O~* 全息图的衍射场总包含三种主要成分:
根据不同的分类方式，可有以下几种类别:
同轴全息图与离轴全息图; 薄全息图与体全息图; 同侧记录全息图与反侧记录全息图; 振幅型全息图与相位型全息图及其彩虹全息图; 菲涅耳全息图与夫琅禾费全息图及其傅里叶全息图; 连续激光全息图与脉冲激光全息图;

光学全息术-1

光学全息术-1

前两项基本上是常数，是直流项，对波前再现无用。
7.2.3式中的第三项、第四项：分别包含了物光波 和物光波的共轭。是物光波对参考光波的调制，参 考光波是载波， 物光波作为调制波。可以用于波 前再现。
7.2.4式的第三项：是由7.2.3中的第三、四项得来， 是干涉项， 清楚地表明：它包含了物光波的振幅和 相位信息。参考光波作为载波，其振幅和相位均受 到物光波的调制(调幅、调相)
在1948年，提出用光波记录物光波振幅和相位的方法，并用 实验证实这一想法，从而产生了一个新的光学领域——光全 息术。1971年，因此获得诺贝尔物理学奖。
二、全息术发展的几个阶段
自1948年伽伯提出光全息的思想一直到50年代末，全息照相 一般采用汞灯作为光源，并且是同轴全息记录方法（得到全 息图称为同轴全息）。±1级衍射波与零级分不开，存在所 谓的“孪 生像”问题，不能获得好的再现图像。光源的相 干性差。 全息术的萌芽时期。第一代全息图。
当再现光波满足一定条件时，可比较准确地再现 原物光波或原物光波的共轭光波。
1. 再现光波是全息记录时的参考光波，即 C(x,y)=R(x,y)：
U4
A
B C D
O
B
A
D C
U1+U2
O 再现
U3
Байду номын сангаасR 记录
C=R
(1).
U 3 R CO x , y R O x , y
2
7.2.8
|R|2是参考光波的强度; 是一实常数(平面波), 或 近似为实常数(球面波)。
U4
U3项，再现原物光波，用 眼睛观察或成像系统观测 时，在原位置观察到原物 体的影像，就象原物体还 在。由于物光波是发散的， 所以观察到是物体的 虚像。

光学全息

光学全息

三、特点 1、全息照相最突出的特点为由它所形成的
三维形象 2、可分割性 3. 全息图可进行多重记录 4. 全息图可同时得到虚像和实像
四、全息图的类型 1、按参考光波与物光波主光线是否同轴来
分类，可分为同轴全息图与离轴全息图 2. 按全息图的结构与观察方式分类，可分 为透射全息图与反射全息图 3. 按全息图的复振幅透过率分类，可分为 振幅型全息图和相位全息图 4. 按全息底片与物的远近关系分类，可分 为菲涅耳全息图(Fresnel hologram)、像 全息图(Image plane hologram)、和傅里 叶变换全息图(Fourier transform
R( x, y) t 0 R0 ( x, y)
O( x, y) t ( x, y) R0 ( x, y)
R0 ( x, y)
为正入射平面波
要求： t ( x, y) t0
②离轴全息图 ⅰ.定义：±1级不同轴的全息图。 ⅱ.产生：用光契记录全息图 sin 参考光产生一倾角θ 0
第五章
Optical Holograph 光学全息
►光学全息概述 ►波前的记录与再现 ►常用全息图的生成与再现 ►体全息 ►平面全息图的衍射效率 ►计算全息及其应用
§ 1. 光学全息概述
一、光学全息的发展历史
发明人：英籍匈牙利人丹尼斯盖伯 （Dennis Gabor) 发明时间：1948年 1960年，第一台激光器问世，解决了相干 光源的问题。 1962年，美国科学家利思和乌帕特尼克斯 提出了离轴全息图
③分析讨论： ⅰ 当a1 0时，无法有效记录 ⅱ 当a2 , a3 an 0时, 记录将会代入附加振幅 变化，使相位信息呈非线性 ⅲ 因此要选择线性度较好的全息干板，使： t ( x, y) a0 a1E ( x, y )

傅里叶光学第7章 全息术

傅里叶光学第7章 全息术
➢ 数字全息术 采用CCD等光电成像器件记录物光和参考光的干涉图，然后在计算机 中通过数字重建，由数字全息图获得全息像。 三维形貌测量、振动测量、全息显微术等许多领域获得应用。
➢ 全息术不仅可用于光波波段，也可用于电子波、X射线、声波和微波波段。
1、引言
✓全息图的基本类型
1.同轴全息图 2.离轴全息图 3.菲涅耳全息图 4.傅里叶变换全息图 5.像全息图 6.模压全息 7.位相全息 8.彩虹全息图 9.体积全息图 10.计算全息
O x, y O0 x, y e j0x,y
引入一相干参考波，该参考波在H上产生 的复振幅分布为
R x, y r0 x, y e jr x,y
那么，两波相遇叠加的总光场是
U x, y O x, y R x, y
对应的强度分布为
称为全息图！全息图实际上是一幅干涉图。 记录介质的作用相当于线性变换器，它把曝光时的入射光强线性地变换为 显影后负片的复振幅透过率：
t x, y t0 I x, y (t0和都是常数)
若假定参考光强在H表面上是均匀的，则
t x, y tb O 2 OR* O*R
2、波前记录与再现 p230
✓全息术的应用
1.全息显示 2.模压全息 3.全息光学元件 4.全息干涉计量 5.全息信息存储
2、波前记录与再现 p227
✓全息成像过程
1、波前记录— 用干涉法记录物光波
干涉图样的记录
2、波前再现— 用衍射法再现物光波
2、波前记录与再现
2.1 波前记录
✓假定记录介质H位于xy平面上，物光波前
在H上产生的复振幅分布为
➢ 若采用参考光波照射全息图，即C(x,y)=R(x,y)，则

(完整版)信息光学专题数字全息

(完整版)信息光学专题数字全息

数字全息实验研究数字全息记录和再现原理，即利用数字全息记录程序和光电器件记录全息图，并将全息图输入计算机，由计算机进行数字再现的方法早在1967年就由Goodman等人提出，现已广泛地应用于数字显微、干涉测量、三维图像识别、医疗诊断等领域。

数字全息用光电器件替代了全息干版，免去了全息干版的冲洗工作以及降低了对全息工作台的隔振要求。

给使用者带来了更大的方便。

实验目的1．熟悉数字全息实验原理和方法；通过观察全息图的微观结构，深入理解全息记录和数字再现的原理。

2．熟悉数字全息记录光路。

3．用CMOS数字摄像头记录物体的全息图。

4．熟悉用全息图数字再现程序对所记录的全息图进行数字再现的过程。

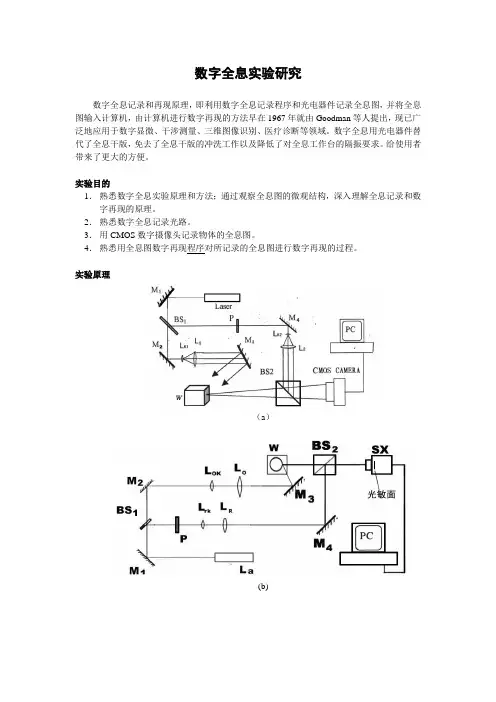
实验原理（a）(b)（c）图1 数字全息实验光路图2. 数字全息记录光路L0k放大倍数20或40；L rk放大倍数60；衰减器P可插入物光束；物体S为透过率物体；BS2与SX之间的物参光方向应相同（夹角为0°）图3 透射数字全息记录系统数字全息波前测量的实验光路随被测物体的不同而异，从图1到图3的光路都可以用来记录全息图。

若用图1（a ）所示的实验光路进行数字全息波前的测量，则激光器发出的光经反射镜M 1反射，被分束器BSI 分成两束；一束经过反射镜M 2反射、进入扩束镜L K1扩束，并被准直镜L 1准直，变成平行光，再由反射镜M 3反射转向，照射到被记录物体上形成物波，经由物体物漫后透过分束镜BS 2照射到数字摄像头的光敏元件表面；另一束经衰减器P 、反射镜M 4、扩束镜L K2准直镜L 2变成平行光，再经分束镜BS 2转向，形成参考光，并与物波在CMOS （或CCD ）光电器件平面上叠加干涉，形成全息图；由CMOS （或CCD ）数字摄像头记录，并借助于计算机程序，实现全息图的数字再现。

图4 数字全息记录与再现光路坐标变换设00oy x 平面内的被记录物体的透过率函数为t (x , y )，用振幅为A 的垂直平面波照明。

光学全息技术原理

光学全息技术原理

光学全息技术原理光学全息技术是一种利用光的干涉原理制作出的三维影像的技术。

全息投影是通过将光波的相位和幅度信息编码到光场中，利用干涉和衍射的原理实现光学全息图像的产生与重建。

它与普通的摄影技术不同，摄影只记录了光强信息，而全息技术还记录了光的相位信息，使得图像更加真实，能够实现如同实物一样的三维空间感。

下面将详细介绍光学全息技术的原理。

光的干涉原理是光学全息技术的基础。

当两束光波相遇时，它们会发生干涉现象。

干涉分为两种类型：相长干涉和相消干涉。

相长干涉是指两束光波在相遇时的干涉，会使得光的幅度增强；相消干涉则是两束光波相遇时产生的干涉，会使得光的幅度减弱或消失。

在光学全息技术中，我们通常使用的物体光源是一束激光光源。

激光光源的特点是具有高度相干性，相干长度长，可以产生明确的干涉图案。

全息图的形成一般可分为三个步骤：记录、显影和重建。

首先是记录过程。

记录过程需要将物体的光波和参考光波进行干涉，将物体光波的信息编码到光场中。

具体操作是将激光通过一个分束镜分成两束，一束作为参考光照射到全息图的记录介质上，另一束经过物体反射或透过后，再与参考光在全息图的记录介质上相遇。

两束光波发生干涉后，形成了全息图的干涉图案。

在光场中，参考光波形成了一种参考波的空间分布，而物体光波也形成了与物体相关的物波的空间分布。

通过这种方式即可将物体的光波信息编码到光场中。

接下来是显影过程。

显影过程是将记录介质中的干涉图案转化为可见的全息图像。

通常采用的方法是将记录介质浸入显影液中，在显影液的作用下，记录介质中光敏材料会经历物理或化学变化，并在光的照射下，显出原本的干涉图案。

经过显影处理后，就得到了全息图，可以在透光条件下观察到清晰的三维图像。

最后是重建过程。

重建过程是将全息图中的光场重新导引出来，使得能够再现物体原始的光波信息。

在重建过程中，使用与记录过程中相同的光源，通过照射到全息图上，使得记录介质中的全息图被激活。

原来记录的参考光与物体光波在全息图上重新重合，发生衍射，从而生成了物体原始的光波，通过屏幕就可以观察到物体的三维图像。

信息光学chap7光学全息

信息光学chap7光学全息
干板记录的是干涉场的光强分布，曝光光强为
I ( x, y) U ( x, y)
2
I ( x, y) U ( x, y)
2
2
R( x, y) O( x, y) R( x, y)O ( x, y) R ( x, y)O( x, y)
＝ R( x, y) O( x, y) ＋2 R( x, y)O( x, y) cos[ ( x, y) ( x, y)]
O ( x, y )
2
具体办法：
R( x, y) O( x, y)
2
2
前两项基本上是常数，第三项是干涉项，作为偏臵项。包 含有物光波的振幅和相位信息。参考光波的作用使物波波前的 相位分布转换成干涉条纹的强度分布。
2、探测
常用的记录介质是银盐感光干板（卤化银乳胶涂敷的超微 粒干板），简称全息干板，对两个波前的干涉图样曝光后，经 显影、定影处理得到全息图。全息干板的分辨率高达3000线/毫 米，甚至更高，全息干板具有足够高的分辨率，以便能记录全 部入射的空间结构。
丹尼斯· 伽柏（Dennis Gabor，1900 年～1979年），英国匈牙利裔物理学 家，1971年诺贝尔物理奖获得者，全 息摄影技术的发明者
§5.1 引言 Introduction
1962年 离轴全息图
问世 ——— Leith 和 Upatnieks
Leith and Upatnieks preparing to shoot a laser transmission hologram using the "off-axis" technique borrowed from their work in the development of side-reading radar. (Photo by Fritz Goro for Life （美） Magazine, 1967)

光学全息原理

光学全息原理

光学全息原理光学全息是一种记录和再现物体波前信息的技术，它利用光的干涉和衍射现象，实现了对物体的三维立体再现。

光学全息的原理基于麦克斯韦方程组和亚伯拉罕-费尔南德斯原理，通过记录物体的全息图像，再通过光的衍射将图像还原出来。

光学全息的基本原理是光的干涉。

当一束平行光照射到物体上时，光束会被物体散射并改变相位和振幅。

在光学全息中，我们将这个散射光束与一个参考光束进行干涉。

干涉是指两束光叠加在一起形成干涉图案。

这个干涉图案记录了物体的相位和振幅信息。

为了记录干涉图案，我们需要使用一种特殊的材料，即全息记录介质。

这种材料能够记录光的相位和振幅信息，并将其永久保存下来。

全息记录介质通常是由光敏材料制成，例如银盐或聚合物。

当干涉图案照射到全息记录介质上时，介质中的光敏材料会发生化学变化或物理变形，从而记录下干涉图案。

在记录全息图像之后，我们可以使用再现装置将图像还原出来。

再现装置通常由一个光源、一个透镜和一个全息记录介质组成。

当光源照射到全息记录介质上时，记录的干涉图案会通过衍射现象再现出来。

透镜的作用是调整光束的焦距，使得再现的图像清晰可见。

光学全息的优点是可以实现真实的三维立体影像。

与传统的摄影技术相比，光学全息可以记录物体的全息信息，包括相位和振幅。

这使得再现的图像更加真实，具有更好的深度感和立体效果。

此外，光学全息还具有较高的信息密度和良好的抗干扰性能。

光学全息在许多领域有着广泛的应用。

在科学研究中，光学全息被用于记录和分析微小物体的形态和运动。

在医学影像学中，光学全息可以用于实现高分辨率的医学图像，帮助医生进行诊断和手术。

在安全领域，光学全息可以用于制作防伪标签和身份证件，提高安全性和防伪能力。

光学全息是一种利用光的干涉和衍射现象记录和再现物体波前信息的技术。

通过记录物体的全息图像，再通过光的衍射将图像还原出来，实现了对物体的三维立体再现。

光学全息具有广泛的应用前景，在科学、医学和安全等领域都有着重要的作用。

信息光学(傅里叶光学)Chap7-2

信息光学(傅里叶光学)Chap7-2
o o 0 o o
U H ℱ O ℱ R O f x , f y f x , f y F F O R

到达记录平面的光复振幅是它们的傅里叶频谱之和：


O ( x
o
, yo ) exp [ - j 2 ( f x xo f y yo ) ] d xo d yo Ro exp [ j 2 f x b]
§7-6 平面全息图
2、傅里叶变换全息图
物光波：O ( xo , yo ) = O0 ( xo , yo ) exp [ jfo ( xo , yo ) ] 参考光: 可利用置于前焦面上的点光源产生，设其位置坐标为 (-b,0)，数学表述为δ 函数： ( x , y ) = R δ ( x + b , y ) R
A
B
例题：P160, 5.2题
解1：采用近轴近似。设点源A、B发出 的球面波在记录平面上的复振幅分布分 别为UA和UB， 并且写为：
UA aA exp jkzA exp ( jk / 2 z A ) ( x - x A ) 2 ( y - y A ) 2 2



x z
A
a U B B exp jkzB exp ( jk / 2 z B ) ( x - xB ) 2 ( y - yB ) 2 2
y
U 曝光光强为 : I ( x , y ) = U ( x , y )· * ( x , y ) =∣O∣2 +∣R∣2 + O· + O*· R* R 全息图的透过率函数tH 与曝光光强成正比：
tH ( x , y ) =|O∣2 +∣R∣2 + O· + O*· R* R

第七章 光学全息

第七章 光学全息

x xc 2 y yc 2 ac U c ( x, y) exp j zc z 2 c
U 3 x, y t3 x, y U c x, y
t3产生的衍射光波为（携带共轭像信息）
x x 0 2 y y 0 2 x x c 2 y y c 2 a0 a r ac x x r 2 y y r 2 exp j j j z0 zr zc 1 z 0 1 z r 2 z c
R（xr,yr,zr） O（x0,y0,z0） x
1
z
满足菲涅耳近似。在干板平面上光场
的复振幅分布分别为
（xc,yc,zc）
2
x x0 2 y y0 2 a0 O( x, y ) exp jk1 z0 2 z0
2 2 x x y y a0 0 0 exp j z0 z 1 0
条纹的间距为
ky(sin r sin 0 ) 2
y d

sin r sin 0
2 sin
r 0
2
光栅频率为
1 sin r sin 0 f f f r 0 d
以上就是拍摄全息光栅的原理。 两束光的夹角越大，条纹越蜜。
条纹取向垂直于两束平行光构成的平面。
第三项包含物光的共轭光波O*(x,y)，第四项包含物光波 O(x,y)。
显影定影后，全息图的透过率为
t ( x, y) I ( x, y) t1 t2 t3 t4
2 2 2 2 a0 ar x x0 y y0 x xr y yr t3 ( x, y) exp j j z0 z r 1z0 1 zr

光学全息原理

光学全息原理

光学全息原理全息术是一种利用光波的干涉和衍射现象来记录和再现物体全息图像的技术。

它采用了光的波动性质，将物体的复杂光学信息以全息图的形式记录下来。

光学全息的原理是基于光的干涉和衍射现象。

在全息术中使用的光源经过分束镜的分光作用，形成了两个光束：物光和参考光。

物光经过物体后，具有物体形状和信息的光波将被记录下来。

参考光则是一个平行光束，它与物光进行干涉。

干涉是指两束光波叠加在一起时，相互加强或减弱的现象。

物光和参考光的干涉会形成一幅干涉图案，该图案记录了物体的各个细节和形状。

接下来，将这个干涉图案转换成全息图。

衍射是光波碰到物体边缘时发生弯曲和散射的现象。

在全息术中，记录下来的干涉图案被照射到光敏材料上，这个材料使得光波发生衍射。

通过对全息图进行照明，可以将物体的原始信息再现出来，形成一个逼真的全息图像。

与传统的平面摄影不同，全息术能够记录下完整的三维信息，包括物体的形状、颜色和光波的相位信息。

这使得全息图像在科学、技术和艺术领域有着广泛的应用。

例如，在生物医学领域，全息术可以用于观察细胞结构和分子运动；在航空航天领域，全息术可以用于制作复杂的光学元件；在艺术领域，全息术可以用于制作具有立体感和动态效果的艺术作品。

光学全息技术的发展已经取得了很大的进展，但仍面临着一些挑战。

例如，全息图的制作过程需要非常稳定的光源和高质量的全息材料。

此外，全息图的再现也需要特殊的照明条件，否则图像可能会失真。

尽管存在一些限制，光学全息技术仍然是一种强大的工具，能够捕捉和再现物体的三维信息。

随着技术的进步，相信全息术将有更广泛的应用领域，给我们带来更多的惊喜和发现。

信息光学复习提纲

信息光学复习提纲

信息光学复习提纲 （自编）第一章 二维线性系统1．空间频率的定义是什么？如何理解空间频率的标量性和矢量性？ 2．空间频率分量的定义及表达式？3．平面波的表达式和球面波的表达式？对于单色光波。

时间量 空间量 22v T πωπ== 22K f ππλ== 时间角频率 空间角频率其中：v ----时间频率 其中：f ---空间频率T----时间周期 λ-----空间周期物理意义： ① 当090,,<γβα时0,,>z y x f f f ， 表示k 沿正方向传播； 当090,,>γβα时0,,<z y x f f f ， 表示k沿负方向传播。

② 标量性， 当α↗时，αcos ↘→x f ↘→x d ↗； 当α↘时，αcos ↗→x f ↗→x d ↘。

③标量性与矢量性的联系 x x f d 1= λαcos =x f条纹密x d ↘→x f ↗→α↘→θ↗条纹疏x d ↗→x f ↘→α↗→θ↘ 可见 ：条纹越密（x d 小），衍射角越大 条纹越疏（x d 大），衍射角越小2．空间频率概念光波的表示式为：(,,)0(,,,)(,,)j t j x y z x y z t x y z e e ωϕμμ-=⋅ 0(,,)jK r j t x y z e e ωμ-=⋅ (1.10.2)显然，光波是时间和空间的函数，具有时间周期性与空间周期性。

3．平面波的表达式 ① 单色平面波的公式 ()()()00,,,cos ,,j t jk r j tU x y z t t k r e e U x y z e ωωμωμ-⋅-=-⋅=⋅= 式中复振幅为：()0,,jk r U x y z e μ⋅=()[]γβαμcos cos cos ex p 0z y x jk ++=令 c z y x =++γβαcos cos cos 可见：等相面是一些平行平面 ②任一平面上的平面波表示式()()()101,,exp cos exp cos cos U x y z jkz jk x y μγαβ=+⎡⎤⎣⎦(()exp exp cos cos 0jkz jk x y μαβ⎡⎤=+⎣⎦ ()[]βαcos cos ex p 0y x jk U +=(1.10.36)令 c y x =+βαcos cos 可见，等位线是一些平行线③用空间频率表示的平面波公式 λαcos 1==x x T f ，1cos y y f T βλ==，1cos z z f T γλ== ()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=z y x j z y x U λγλβλαπμcos cos cos 2exp ,,0 ()()[]z f y f x f j z y x U z y x ++=πμ2ex p ,,0 4、球面波的表达式 ⑴ 单色球面波的复振幅 发散波：(k 与γ一致) ()()0,,,,,jkr j t j t a U x y z t e e U x y z e r ωω--==式中： ()0,,jkr a U x y z e r = (1.10.5) 会聚波：(k 与γ 反向)()()0,,,,,jk r j t j t aU x y z t e e U x y z e r ωω-⋅--==式中： ()0,,jkr a U x y z e r-= (1.10.6)r ⑵ 球面波光场中任一平面上的复振幅分布 设球面波中心与坐标原点重合，则y x ,平面上的复振幅为 ()01,,jkr aU x y z e r=220121exp 12a x y jkz r z ⎡⎤⎛⎫+=+⎢⎥ ⎪⎝⎭⎣⎦ ()⎪⎫ ⎛+⋅≈220exp exp y x jk jkz a4．相干照明下物函数复振幅的表示式及物理意义？5．非相干照明下物光强分布的表示式及物理意义？1、 相干照明设()y x f ,为一物函数的复振幅，其傅氏变换对为 ()()(),exp 2x y x y F f f f x y j f x f y dxdyπ∞-∞⎡⎤=-+⎣⎦⎰⎰ ()()(),,exp 2xyxyxyf x y F f f j f x f y d f dfπ∞-∞⎡⎤=+⎣⎦⎰⎰可见：物函数()y x f ,可以看作由无数振幅不同方向不同的平面波相干迭加而成。

光学全息技术原理

光学全息技术原理
+ R 0 2 O 0 exp [ j (φo -2φr )]+ R 0 2 O 0 exp [ - jφo]
第一、二项合并，仍保存了参照光旳特征 第三项是畸变了旳虚象 第四项是与原物相象旳实像，但出现了景深反演，即原来近旳部位
变远了，原来远旳部位变近了，称为赝像
波前再现旳几种特例(3)
(3)其他情况： a．照射角度旳偏离：如再现光与参照光波面形状相同，只是相对全
盖伯防止位相信息丢失旳技巧是干涉措施,因为干涉场分布与波面位 相有一一相应关系
物光波旳振幅和位相信息便以干涉条纹旳形状、疏密和强度旳形式 “冻结”在感光旳全息干板上
波前统计和波前再现示意图
波前统计旳数学模型
在全息干板H上设置x , y坐标，设物波和参照波旳复振幅分别为 O ( x , y ) = O 0 ( x , y ) exp [ jφo ( x , y ) ] R ( x , y ) = R 0 ( x , y ) exp [ jφr ( x , y ) ]
离轴全息图
统计离轴全息图旳光路
离轴全息图统计光路如下图所示，准直光束一部分直接照射物 体（透明物体），另一部分经物体之上旳棱镜P偏折，以倾角 投射到全息干板上。全息干板上旳复振幅分布应是物体透射波 和倾斜参照波叠加旳成果，即有
P
y
物体
U ( x, y) Aexp j2 y O( x, y)
H胶片
均匀旳平面波，它相当于波前统计时旳参照波；另一项是 t
所代表旳弱散射波，它相当于波前统计时旳物光波。
在距离物体 z0处放置全息图干板时旳曝光光强为：
I (x, y) R O(x, y) 2 R~2 O(x, y) 2 RO*(x, y) R*O(x, y)

光学全息技术介绍

光学全息技术介绍

彩虹全息技术
原理
在全息图的记录过程中，采用不同角 度的参考光束，形成具有不同波长选 择性的干涉条纹，从而在白光下呈现 出彩虹般的效果。
特点
具有绚丽的视觉效果和较高的防伪性 能，广泛应用于证件、商标等领域。 但成像质量受光源影响较大。
数字全息技术
原理
利用计算机技术和数字图像处理技术对全息图进行记录和重现，实现全息图的数字化存储、传输和处 理。
特点
具有灵活性高、处理速度快、易于实现远程传输和自动化处理等优点。同时，数字全息技术还可以与 其他成像技术相结合，实现多模态成像和复合成像等高级功能。
03 光学全息技术应用领域探 讨
三维显示与虚拟现实应用
三维显示
光学全息技术能够记录并再现物体的三维信息，使得观察者能够从不同角度看到物体的不同侧面，从而实现真正 的三维显示。
发展历程
全息技术自20世纪40年代提出以来，经历了不断的发展和完 善。从最初的同轴全息术到离轴全息术，再到后来的数字全 息术，全息技术在不断突破中实现了更高的图像质量和更广 泛的应用领域。
光学全息技术原理简述
记录过程
在记录过程中，使用一束相干光（通常是激光）照射物体，另一束相干光作为 参考光与物体反射或透射的光在记录介质上干涉，形成全息图。全息图记录了 物体的振幅和相位信息。
特点
具有高分辨率、大视角、真彩色 三维立体成像等优点，但需要使 用激光作为光源，且对环境稳定 性要求较高。
反射式全息技术
原理
在全息图的记录过程中引入反射相移 ，使得全息图可以在普通白光下通过 反射方式观察到三维立体像。
特点
无需特殊光源，可在自然光下观察， 且观察角度较大。但分辨率和色彩还 原度相对较低。
曝光记录

信息光学7

信息光学7
7
磨镜者公式：
1 f
(n1)R11
1 R2
8
如果用单位振幅的平面波入射到透镜上，这时入射波复振幅，
U1(x,y)1
出射光波复振幅，
U 2 (x ,y ) U 1 (x ,y )P L (x ,y )expi2kf
(x2y2)
9
2. 透镜的傅立叶变换性质 会聚透镜最突出的的性质之一就是它固有的进行二维傅立叶变换 的本领。 假定光源是单色的，也就是说我们所研究的系统是相干系统。 我们讨论一下正透镜后面某个特定平面上的复振幅分布。
如图所示，O点发出的发散球面波，经过透镜后，会聚到I点。
2
由菲涅耳近似，O点发出的 球面波到达P1平面上(x,y) 点处时，其复振幅：
U1(x,
y)
A d1
exp(
ikd 1 )
•
exp
i
k 2d1
(x2
y
2
)
略去与位置(x,y)无关的A/d1因子，
U 1(x,y)exip k1)(d ex ip 2k d1(x2y2)
上式已略去常量相位因子，将gt(x,y)代入上式，化简，
g ( x 0 ,y 0 ) iA d 2 efix d (f p x 2 fy 2 ) F f( x ,y )
i A d2fex i2 p k d(x0 2y0 2) F(fx,fy)
其中
fx
x0 ,
d
fy
y0
d
18
g (x 0 ,y 0 ) iA d 2e f x i2 k d p (x 0 2 y 0 2 ) F (fx,fy)
我们知道，频谱面P4上任一点P’(x’,y’)的光场应该是物所有 点发出的方向余弦x’/f,y’/f的光线经过透镜会聚叠加而形成。

信息光学第07章

信息光学第07章

(7.1.4)
上式表明，两束光波在空间 P 点的合振动强度由三项组成，即两束波各自独立传播时在的振动 I1 ( P, t ) 、
I 2 ( P, t ) 和两束光在 P 点相互作用的互强度—交叉项 2 Re{u1 ( P, t )u2 ( P, t )} 。当这个交叉项为等于 0 时，
P 点的合振动强度将不再简单地等于两光束独立传播时在 P 点引起的振动强度之和。 波动的这种叠加现象
第七章
部分相干理论
通过前几章的讨论，我们可以看到，照射光源的相干性对光学系统成像具有极大的影响。 所谓相干性(coherence)，是指两列同频率的单色光波叠加时，彼此相关而能够观察到清晰的 干涉现象。它包含了相干的时间效应和空间效应，这两种效应分别产生于光源的单色性程度 和光源的有限尺寸。相干性的好坏常用其干涉条纹的对比度来描述。在实际问题的处理过程 中，为了简便起见，作了两种理想化的假设：一种情况是把光源假设为一个理想的点光源， 且具有严格的单色性，这样的光振动具有完全的相干性，其干涉条纹的对比度可以达到 1； 另一种情况则假设光源是完全不相干的，用完全不相干的光源照明时得不到干涉条纹，干涉 图的对比度等于 0。 但是，点光源和单色光都是一种理想化的抽象。严格的单色光在时间上是无限延续的， 传播的波列也是无限长的，这自然在实际中是不存在的。同样，严格的点光源也是一种理想 模型，同样也是不存在的。任何光源都包含有一定的波长范围和尺寸，这就会影响到光源的 相干性。与此对应，完全不相干的光源也是一种理想化模型，即使采用通常认为完全不相干 的太阳光束照射，在一定条件下也能产生干涉效应。例如，在杨氏干涉装置中，只要两个小 孔靠得很近(约 0.02 mm)，用太阳光来照射双孔，也能看到干涉条纹。由于严格相干场和严格 的非相干场实际上都不可能得到，因此，应该研究实际存在于完全相干与完全不相干之间的 中间状态，称为部分相干性 (partial coherence)，这就是本章所要讲述的内容。 部分相干理论是现代光学中较为活跃的一个研究领域，它既是处理光场统计性质的一种 理论(统计光学方法)，又涉及光场的量子力学描述(量子光学)。这里，我们仅限于讲述部分相 干理论的基本概念和基本规律，只采用对光场的统计描述，而不涉及量子光学处理方法。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1965年 1968年 ......
40多年来，全息学科和技术得到飞速发展，高科技、国防、 艺术等领域几乎无所不及。
1、引言
全息发展的四个阶段
第一阶段 汞灯作光源，同轴全息图
—— 萌芽阶段 第一代全息 第二阶段 激光记录，激光再现，离轴全息图 ——第二代全息* 第三阶段 激光记录，白光再现 ——第三代全息* 第四阶段 白光记录，白光再现 ——第四代全息
1、引言
全息技术的典型代表—全息照相
波前记录— 用干涉法记录物光波
波前再现— 用衍射法再现物光波
1、引言
什么是全息术？
全息术（holography）是利用光的干涉和衍射原理， 将携带物质信息的光波以干涉图的形式记录下来， 并且在一定的条件下使其再现，形成原物体逼真的
立体象。由于记录了物体的全部信息，包括振幅和
提出“斜参考光法”, 加速了全息术的发展
1962年
U.Denisyuk 提出反射全息图的方法；
1、引言 1964年
Ar+ Laser 问世 —— 布里奇斯 氩离子激光器提供了短波长连续可见光，扩展
了全息技术 的应用范围 R.L.鲍威尔，K.A.斯特特森 提出全息干涉术； S.A.本顿 发明彩虹全息术（白光全息术）；
U4 x, y RO*R R2O* x, y
不考虑常数因子的影响，U3是原始物光波的准确复现，给出物体的一个虚像； O*是物光波前的共轭，若原始物波是发散的，则共轭光波是会聚的，因此U4 的传播将给出物体的一个实像。此时，虚像没有变形，而实像有变形。
2、波前记录与再现
2 2 2
物光和参考光的强度 干涉项中包含了物体光波振幅和位相信息！
干涉项
2、波前记录与再现
两个波前的干涉图样通过曝光经显影处理后将全部记录到记录介质上，
称为全息图！全息图实际上是一幅干涉图。 记录介质的作用相当于线性变换器，它把曝光时的入射光强线性地变换为 显影后负片的复振幅透过率：
t x, y t0 I x, y
(t0和都是常数)
若假定参考光强在H表面上是均匀的，则
t x, y tb O OR* O* R
2
2、波前记录与再现
2.2 波前再现
用参考波照明
用共轭参考波照明
2、波前记录与再现
用相干光波照射全息图，假定它在全息图平面上的复振幅分布为C(x,y)，
二十世纪光学领域三件大事：
1948年：全息术的诞生 1955年：光学传递函数 1960年：激光诞生
现代 光学
信息光学 (傅立叶光学) 非线性光学 (强光光学)
为提高电子显微镜分辨本领，伽伯（D.Gabor，1900—1979）在1948
年提出了全息术原理，并开始了全息照相(holography)的早期研究工作， 并因此在1971年获得诺贝尔物理学奖。
全息成像过程
1、波前记录— 用干涉法记录物光波
干涉图样的记录
2、波前再现— 用衍射法再现物光波
2、波前记录与再现
2.1 波前记录
假定记录介质H位于xy平面上，物光波前
在H上产生的复振幅分布为
O x, y O0 x, y e j0 x , y
引入一相干参考波，该参考波在H上产生 的复振幅分布为
相位因此称为全息术。
1、引言
全息发展简史

1948年
Dennis Gabor 提出 光源：汞灯
“波前重现”
理论
目的：改善电子显微镜的分辨率 效果：因光源相干性差，效果很不明显
1960年
激光器 问世， 提供 理想的相干光源
为全息技术的发展创造了条件
1962年
离轴全息图问世 ——E.N.Leith和J.Upatnieks
思考题：P290 -7.1 若一个平面物体的全息图记录在与物体平行的记录介质上， 证明再现像将成在与全息图平行的平面内(为简单起见，假 定参考波为平面波)。
3、同轴全息图与离轴全息图
只有使全息图衍射光波中各项有效分离，才能得到可供利用的再现像， 这与参考光方向的选取有直接的联系。下面分两种情况讨论： 3.1 同轴全息图
若采用共轭参考光照明全息图，即C(x,y)=R*(x,y)，则
U3 x, y R*OR* R*2O x, y
U 4 x, y R*O* R R O* x, y
2
U3和U4仍正比于物光波前或其共轭，将分别产生虚像和实像； 此时，虚像有变形，实像没有变形。
R x, y r0 x, y e jr x, y
那么，两波相遇叠加的总光场是
U x, y O x, y R x, y
对应的强度分布为
I x, y U x, y O x, y R x, y O x, y R* x, y O* x, y R x, y
为使成像光波和晕轮光U2有效分离，G2、G3和G4之间不能重叠，则必须满 足条件： 3 f M 或 sin 3 f M
4、基元全息图分析
全息图可看作是很多基元全息图的线性组合，了解基元全息图的结构和
作用对于深入理解整个全息图的记录和再现机理非常有益。 空域方法是把物体看作一些相干点源的集合，物光波前是所有点源发出的 球面波的线性叠加。每一个点源发出的球面波与参考波干涉，记录的基元 全息图称为基元波带片； 频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加， 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
普通高等教育“十一五”国家级规划教材 《傅里叶光学•第2版》电子教案
第七章 光学全息 周哲海 吕乃光 编著
机械工业出版社
本章主要内容
1、引言
2、波前记录与再现 3、同轴全息图和离轴全息图 4、基元全息图分析 5、几种不同类型的全息图
6、体积全息图
7、计算全息图 8、记录介质 9、全息术的应用
1、引言
全息图的透射光场分布为
U t x, y Ct x, y Ctb C O COR* CO* R U1 U 2 U 3 (x,y)=R(x,y)，则 2 U 3 x, y ROR* R O x, y
2、波前记录与再现 波前记录是一种干涉效应，它使振幅和位相调制信息变换为干
涉图的强度调制信息； 波前再现是一种衍射效应，胶片经过线性处理后，使全息图上 的强度调制信息还原为波前的振幅和位相调制信息。
既然全息术基于光的干涉和衍射现象，系统就应满足一定的相
干性要求，例如激光输出波长稳定、曝光期间装臵稳定、两束光 的最大光程差应比光的相干长度小得多等。
I x, y r0 O x0 , y0 r02 O r0O r0O*
2
3、同轴全息图与离轴全息图
经过显影、定影后，负片的复振幅透过率就正比于曝光强度，即
t x, y tb O r0O r0O*
2


若用一平面波垂直照明全息图，透射光场为
x x0 2 y y0 2 O x, y O0 exp j 1 z0
4、基元全息图分析
这样制成的全息图，当用另一波长2，位于 点源（xc,yc,zc)发出的球面波
x xc 2 y yc 2 U c x, y C0 exp j 2 zc
3、同轴全息图与离轴全息图
3.2 离轴全息图 透射光波为：
U t x, y C0tb C0 O
2
C0r0O x, y exp j 2 y
C0r0O* x, y exp j 2 y
U1 U 2 U3 U 4
1、引言
全息图的基本类型
1.同轴全息图 2.离轴全息图 3.菲涅耳全息图 4.傅里叶变换全息图 5.像全息图 6.模压全息 7.位相全息 8.彩虹全息图 9.体积全息图 10.计算全息
全息术的应用
1.全息显示 2.模压全息 3.全息光学元件 4.全息干涉计量 5.全息信息存储
2、波前记录与再现
a) 同轴全息图的波前记录
伽柏全息图就是一种同轴全息图，参考光和物光都沿着光轴的方向。假设用相干 平面波照明一高度透明的物体，其复振幅透过率可表示为
t x0 , y0 t0 t x0 , y0
由t0透过的均匀平面波作参考光，而t项所产生的衍射光作物光O(x,y)，则两者在 胶片上的曝光强度为 2
1
公式正负号中上面一组符号对应于U3，下面一组符号对应于U4。
可根据像点位臵判断像的虚实。像点与物点在全息图同一侧，得虚像； 否则得实像。像的横向放大倍数为
dx dy z z z M i i 2 i 1 0 1 0 dx0 dy0 1 z0 zr 2 zc
1
其中，=sin/，参考波的空间频率。 U1：衰减的照明光波； U2：透射光锥，晕轮光； U3：向下倾斜的虚像； U4：向下倾斜的实像。
波前记录
波前再现
3、同轴全息图与离轴全息图
从频率域的角度考虑离轴全息图。假定物体最高空间频率为fM周/mm，则 如下图：U3和U4的频谱G3和G4分别位于(0,)和(0,-)处。
平面波照明位于透镜前焦面的物体（透明片），同一平面上，离开光轴距离为b 处有一相干的参考点源。前焦面上总的光场为
U x0 , y0 g x0 , y0 r0 x0 , y0 b
根据透镜的傅立叶变换性质，后焦面上的光场为
U f x , f y G f x , f y r0 exp j 2 bf y
U t x, y C0tb C0 O C0 r0O C0 r0O*