matlab旋转+双线性插值

Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1，其调用格式为： yi= interp1(x,y,xi,'method')其中x，y为插值点，yi为在被插值点xi处的插值结果；x,y为向量， 'method'表示采用的插值方法，MATLAB提供的插值方法有几种： 'method'是最邻近插值， 'linear'线性插值； 'spline'三次样条插值； 'cubic'立方插值．缺省时表示线性插值注意：所有的插值方法都要求x是单调的，并且xi不能够超过x的范围。

例如：在一天24小时内，从零点开始每间隔2小时测得的环境温度数据分别为12，9，9，10，18 ，24，28，27，25，20，18，15，13，推测中午12点（即13点）时的温度．x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为： 27.8725若要得到一天24小时的温度曲线，则：xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值（表格查找）。

该命令对数据点之间计算内插值。

它找出一元函数f(x)在中间点的数值。

其中函数f(x)由所给数据决定。

x：原始数据点Y：原始数据点xi：插值点Yi：插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi，每一元素对应于参量xi，同时由向量x 与Y 的内插值决定。

参量x 指定数据Y 的点。

若Y 为一矩阵，则按Y 的每列计算。

yi是阶数为length(xi)*size(Y,2)的输出矩阵。

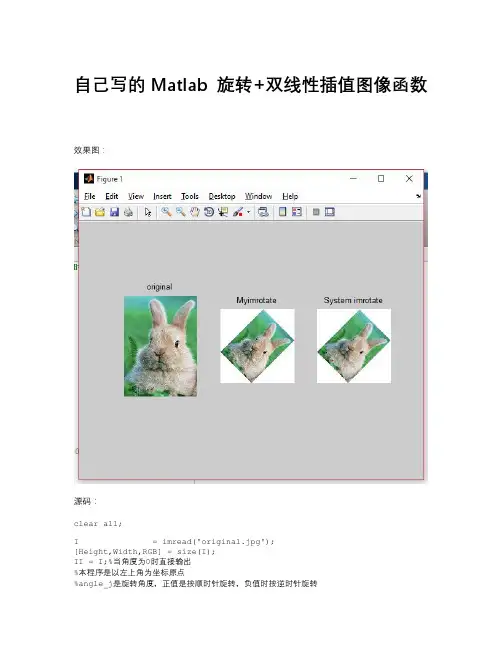
自己写的Matlab 旋转+双线性插值图像函数效果图：源码：clear all;I = imread('original.jpg');[Height,Width,RGB] = size(I);II = I;%当角度为0时直接输出%本程序是以左上角为坐标原点%angle_j是旋转角度，正值是按顺时针旋转，负值时按逆时针旋转angle_j = 181;%angle是弧度angle = 2*pi*angle_j/360;%将angle转成正值while(angle < 0)angle = 2 * pi + angle;end%约束在0-2π内while(angle > 2 * pi)angle = angle - 2 * pi;end%tag是判断下面的while循环有没有执行过tag = 0;while(angle > 0)%超过90度的旋转，都先旋转90度，直到角度在0°-90°之间%原理是旋转90度整数倍时，信息是不丢失的if angle >= pi/2a = pi/2;angle = angle - pi/2;elseif 0 < angle < pi/2a = angle;angle = 0;endif tag == 0tag = 1;elseI = II;[Height,Width,RGB] = size(I);%在旋转后的图像上继续旋转，从而实现大于90°的旋转end%正向变换用sina = sin(a);cosa = cos(a);%逆向变换用_m == _minussina_m = sin(-a);cosa_m = cos(-a);%旋转后图像的长度和宽度II_height = round(sina * Width + cosa * Height);II_width = round(sina * Height + cosa * Width);II = ones(II_height,II_width,3);%先转成unit8。

Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1，其调用格式为：yi= interp1(x,y,xi,'method')其中x，y为插值点，yi为在被插值点xi处的插值结果；x,y为向量， 'method'表示采用的插值方法，MATLAB提供的插值方法有几种： 'method'是最邻近插值， 'linear'线性插值； 'spline'三次样条插值； 'cubic'立方插值．缺省时表示线性插值注意：所有的插值方法都要求x是单调的，并且xi不能够超过x的范围。

例如：在一天24小时内，从零点开始每间隔2小时测得的环境温度数据分别为12，9，9，10，18 ，24，28，27，25，20，18，15，13，推测中午12点（即13点）时的温度．x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为： 27.8725若要得到一天24小时的温度曲线，则：xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值（表格查找）。

该命令对数据点之间计算内插值。

它找出一元函数f(x)在中间点的数值。

其中函数f(x)由所给数据决定。

x：原始数据点Y：原始数据点xi：插值点Yi：插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi，每一元素对应于参量xi，同时由向量x 与Y 的内插值决定。

参量x 指定数据Y 的点。

若Y 为一矩阵，则按Y 的每列计算。

yi 是阶数为length(xi)*size(Y,2)的输出矩阵。

matlab多项式插值函数
在MATLAB中，多项式插值函数可以通过使用interp1、
interp2和interp3等函数来实现。

其中，interp1用于一维插值，interp2用于二维插值，interp3用于三维插值。

这些函数可以用来在给定的数据点上进行插值，生成一个平滑的曲线或曲面。

以interp1为例，可以使用以下语法进行多项式插值：
matlab.
interp1(x, y, xi, 'method')。

其中，x和y分别是原始数据点的横坐标和纵坐标，xi是要进行插值的点的横坐标，'method'是插值方法，可以选择 'linear'（线性插值）、'nearest'（最近邻插值）、'spline'（样条插值）或 'pchip'（分段三次 Hermite 插值）等。

除了interp1之外，还可以使用polyfit和polyval函数进行多项式插值。

polyfit用于拟合多项式系数，polyval用于计算插值点的函数值。

在实际使用中，可以根据具体的数据特点和需要选择合适的插值方法，以及适当的多项式次数，来实现多项式插值函数的应用。

总之，MATLAB提供了丰富的函数和工具，可以帮助我们实现多项式插值，并且可以根据具体情况选择合适的方法和参数进行插值计算。

希望以上信息能够帮助到你。

插值方法晚上做一个曲线拟合，结果才开始用最小二乘法拟合时，拟合出来的东西太难看了！于是尝试用其他方法。

经过一番按图索骥，终于发现做曲线拟合的话，采用插值法是比较理想的方法。

尤其是样条插值，插完后线条十分光滑。

方法付后，最关键的问题是求解时要积分，放这里想要的时候就可以直接过来拿，不用死去搜索啦。

呵呵插值方法的Matlab实现一维数据插值MATLAB中用函数interp1来拟合一维数据，语法是YI = INTERP1(X,Y,XI,方法)其中（X，Y）是已给的数据点，XI 是插值点，其中方法主要有'linear' -线性插值，默认'pchip' -逐段三次Hermite插值'spline' -逐段三次样条函数插值其中最后一种插值的曲线比较平滑例：x=0:.12:1; x1=0:.02:1;%（其中x=0:.12:1表示显示的插值点，x1=0:.02:1表示插值的步长）y=(x.^2-3*x+5).*exp(-5*x).*sin(x);plot(x,y,'o'); hold on;y1=interp1(x,y,x1,'spline');plot(x1,y1,':')如果要根据样本点求函数的定积分，而函数又是比较光滑的，则可以用样条函数进行插值后再积分，在MATLAB中可以编写如下程序：function y=quadspln(x0,y0,a,b)f=inline('interp1(x0,y0,x,''spline'')','x','x0','y0');y=quadl(f,a,b,1e-8,[],x0,y0);现求sin(x)在区间[0，pi]上的定积分，只取5点x0=[0,0.4,1,2,pi];y0=sin(x0);I=quadspln(x0,y0,0,pi)结果得到的值为2.01905，精确值为2求一段matlab插值程序悬赏分：20 - 解决时间：2009-12-26 19:57已知5个数据点：x=[0.25 0.5 0.75 1] y=[0 0.3104 0.6177 0.7886 1] ，求一段matlab插值程序，求过这5个数据点的插值多项式，并在x-y坐标中画出y=f（x）图形，并且求出f （x）与x轴围成图形的面积（积分），不胜感激！使用Lagrange 插值多项式的方法：首先把下面的代码复制到M文件中，保存成lagranfunction [C,L]=lagran(X,Y)% input - X is a vector that contains a list of abscissas% - Y is a vector that contains a list of ordinates% output - C is a matrix that contains the coefficients of the lagrange interpolatory polynomial%- L is a matrix that contains the lagrange coefficients polynomialw=length(X);n=w-1;L=zeros(w,w);for k=1:n+1V=1;for j=1:n+1if k~=jV=conv(V,poly(X(j)))/(X(k)-X(j));endendL(k,:)=V;endC=Y*L;然后在命令窗口中输入以下内容：x=[0 0.25 0.5 0.75 1];y=[0 0.3104 0.6177 0.7886 1];lagran(x,y)ans =3.3088 -6.3851 3.3164 0.7599 0得到的数据就是多项式各项的系数，注意最后一个是常数项，即x^0，所以表达式为:f=3.3088*x.^4-6.3851*x.^3+3.3164*x.^2 +0.7599*x求面积就是积分求解>> f=@(x)3.3088*x.^4-6.3851*x.^3+3.3164*x.^2 +0.7599*x;>> quad(f,0,1)ans =0.5509这些点肯定是通过这个多项式的！MATLAB插值与拟合§1曲线拟合实例：温度曲线问题气象部门观测到一天某些时刻的温度变化数据为：试描绘出温度变化曲线。

matlab 插值法MATLAB 插值法是数据处理和信号处理中常用的一种算法。

在数据采集或数据处理中，通常会遇到数据缺失或者采样点不足的情况，这时候就需要用到插值法来对数据进行补充或者重构。

插值法的基本思想是，给定一些离散的数据点，通过一种数学方法，构造出一个连续的函数，使得在已知数据点处，该函数与原数据点一致。

常见的插值方法有线性插值、多项式插值、样条插值等。

线性插值法是最简单的一种插值方法。

在采样点之间的区域内，采用一次多项式函数去逼近该区域内的某个未知函数。

其公式如下所示：f(x) = f(x0)(1 - t) + f(x1)t其中，x0 和 x1 是相邻两个采样点，t 是一个权重系数，表示该点在两个采样点之间的位置。

多项式插值法是用一个 n 次多项式函数逼近原函数 f(x)。

在采样点处，两个函数的取值相同，同时也能保证一定的光滑性。

其公式如下所示：f(x) = a0 + a1x + a2x^2 + ... + anxnS''(x) = M0(x - x0) + N0, x0 ≤ x ≤ x1其中，M 和 N 是未知的系数，通过计算两个相邻区间中的连续性和光滑性来解出系数。

除了以上三种插值方法，还有其他的插值算法，例如离散傅里叶插值法、拉格朗日插值法等。

总之，MATLAB 中的插值函数为 interp1，它的语法格式如下：yi = interp1(x, y, xi, method)其中，x 和 y 为已知函数的取值点，xi 为要进行插值的点的位置，method 是采用的插值方式。

例如，method = 'linear' 表示采用线性插值法。

MATLAB 中还提供了很多其他的 method 选项，用户可以根据实际情况选择适合的方法。

MATLAB 插值算法在信号处理和图像处理中广泛应用，例如，图像的放大缩小、色彩调整、去噪等都可以用插值算法实现。

因此，掌握 MATLAB 插值算法可以帮助我们更好地进行数据处理和信号处理。

% 本程序实现双线性插值% 对于取整% there is a decimal a, the value of round and ceil is the nearest integer >a;% on the contrast, floor and fix is the nearest integer <a;% round = ceil ；floor = fix% 双线性插值：% 输出像素值是它在输入图像中2*2邻域采样点的平均值，% 它根据某像素周围4个像素的灰度值在水平和垂直两个方法上对其插值。

为了方便理解，先考虑一维情况下的线性插值：% 对于一个数列c，% 假设c[a]到c[a+1]之间是线性变化的，那么对于浮点数% %-------------------第一种表达% x( a <= x < a+1)% c(x) = c[a+1]*( x - a) + c[a]*( 1 + a - x);% c(x) = c[a] + [ (c[a+1]-c[a])/(b-a)]*( x - a);% b = a+1;% c(x) = c[a] + [ c[a+1] - c[a]]*( x - a);% 把这种插值方式扩展到二维情况：对于一个二维数组c，% 我们假设对于任意一个浮点数i,c(a,i)到c(a+1,i)之间是线性变化的,c(i,b)到c(i,b+1)之间也是线性变化的(a,b都是整数) ，% 那么对于浮点数的坐标(x,y)满足(a <= x < a+1, b <= y < b+1)，可以先分别求出c(x,b)和c(x,b+1):% c(x,b) = c[a+1][b]*( x - a) + c[a][b]*( 1 + a - x);% c(x,b+1) = c[a+1][b+1]*( x - a) + c[a][b+1]*( 1 + a - x);% 好，现在已经知道c(x,b)和c(x,b+1)了，而根据假设c(x,b)到c(x,b+1)也是线性变化的，所以:% c(x,y) = c(x,b+1)*( y - b) + c(x,b)*( 1 + b - y)% %------------第二种表达% c(x) = c[a+1]*( x - a) + c[a]*( 1 + a - x);% = c[a] + c[a+1]*( x - a) - c[a]( x - a);% c(x) = c[a] + ( c[a+1] - c[a])*( x - a);% 对于二维情况：% c(x,b) = c[a,b] + ( c[a+1,b] - c[a,b])*( x - a);% c(x,b+1) = c[a,b+1] + ( c[a+1,b+1] - c[a,b+1])*( x - a);% c(x,y) = c(x,b) + ( c(x,b+1) - c(x,b))*( y - b);%---------------------------------------------------------------------clc;clear all;Image = imread('1218.bmp');grayImage = rgb2gray(Image);figure,imshow(Image);figure,imshow(grayImage);% grayImage = [1 2 3 4 5;1 2 3 4 5;1 2 3 4 5;1 2 3 4 5;1 2 3 4 5];% grayImage = [1 2 3;1 2 3;1 2 3];rotation = [0.5 0.5;-0.5 0.5];[rows cols] = size(grayImage);grayImage = double(grayImage);for r = 1:rowsfor c = 1:colstemp = rotation*[r-rows/2;c-cols/2]+[rows/2;cols/2]; % 旋转% temp = [rows/2;cols/2];if( temp(1)>1 && temp(2)>1 && temp(1)<rows && temp(2)<cols) % 双线性插值x = floor(temp(1));y = floor(temp(2));% 插值公式1% v1 = grayImage( x+1,y)*( temp(1)-x) + grayImage( x,y)*( 1+x-temp(1));% v2 = grayImage( x+1,y+1)*( temp(1)-x) + grayImage( x,y+1)*( 1+x-temp(1)); % v = v2*( temp(2)-y) + v1*( 1+y-temp(2));% 插值公式2v1 = grayImage(x,y) + ( grayImage(x+1,y) - grayImage(x,y))*( temp(1) - x);v2 = grayImage(x,y+1) + ( grayImage(x+1,y+1) - grayImage(x,y+1))*( temp(1) - x);v = v1 + ( v2 - v1)*( temp(2) - y);grayImageN(r,c) = round(v);endendendgrayImage = uint8(grayImageN);figure,imshow(grayImage);本文来自: 高校自动化网() 详细出处参考(转载请保留本链接)：/html/matlab/15410_2.html。

实验三图像的几何操作一、图像的基本运算1、加法运算图像相加一般用于对同一场景的多幅图像求平均效果，以便有效地降低具有叠加性质的随机噪声。

直接采集的图像品质一般都较好，不需要进行加法运算处理，但是对于那些经过长距离模拟通信方式传送的图像（如卫星图像），这种处理是必不可少的。

在MA TLAB7.0中，如果要进行两幅图像的加法，或者给一幅图像加上一个常数，可以调用imadd函数来实现。

imadd函数将某一幅输入图像的每一个像素值与另一幅图像相应的像素值相加，返回相应的像素值之和作为输入图像。

imadd函数的调用格式可参考图像处理的工具箱。

下面的程序可将图1两幅图像叠加在一起，叠加效果如图2所示。

imshow('rice.png');imshow('cameraman.tif');I=imread('rice.png');J=imread('cameraman.tif');K=imadd(I,J,'uint16');%大小必须一样imshow(K,[])图1 图2给图像的每一个像素加上一个常数可以使图像的亮度增加。

例如以下程序示例的处理效果如图3所示。

I=imread('rice.png');J=imadd(I,50);subplot(1,2,1),imshow(I);subplot(1,2,2),imshow(J);图32、减法运算图像减法也称为差分方法，是一种常用于检测图像变化及运动物体的图像处理方法。

图像减法可以作为许多图像处理过程的准备步骤。

例如，可以使用图像减法来检测一系列相同场景图像的差异。

图像减法与阈值化处理的综合使用通常是建立机器视觉系统最有效的方法之一。

当然，在利用图像减法处理图像时，往往需要考虑背景的更新机制，尽量补偿因天气、光线等因素对图像显示效果造成的影响。

在MATLAB7.0中，使用imsubtract函数可以将一幅图像从另一幅图像中减去，或者从一幅图像中减去一个常数。

matlab插值函数Matlab（矩阵实验室）是一种高级的数学软件，它可以帮助人们解决复杂的数学和工程问题。

其中最重要的功能之一就是插值函数。

插值函数是一种在非等间距的数据点之间通过计算曲线或其他曲面来估算未知值的技术。

本文将就插值函数在MATLAB中的发挥，以及MATLAB提供的插值函数进行详细的介绍。

一、关于MATLAB插值函数的简介MATLAB的插值函数是一种估算未知值的方法，它可以帮助人们在非等间距的数据点之间通过计算曲线或其他曲面来估算未知值。

使用插值函数，可以从已知数据中推断未知数据。

MATLAB插值函数可以用于曲线拟合、寻找特定函数极值、以及求解线性和非线性方程组。

一般来说，使用插值函数进行重新排列或插值时，数据点之间的距离应尽量小，而不是间歇的大距离。

二、MATLAB提供的插值函数MATLAB拥有多种内置的插值函数，以下是MATLAB中最常用的几种插值函数：1.性插值：Linear interpolation，它将所求点放在两个已知点之间，并使用两个已知点的线性函数值来拟合它；2.式插值：多项式插值是使用一组已知点拟合一个多项式来估算未知点的最小二乘法插值法；3.条插值：样条插值是利用一些已知点来拟合出一个连续可微的样条函数来进行插值处理的；4.数插值：指数插值是根据一些已知的指数函数拟合出曲线来做插值处理的。

三、MATLAB插值函数的应用MATLAB插值函数的应用非常广泛，它可以用来解决和处理复杂的数学和工程问题。

例如，可以使用MATLAB插值函数来拟合数据；对解决非线性方程组有很大帮助；可以将数据绘制出来，以便于观察、比较、识别出特殊的性质；还可以用来估算未知函数值；最后还可以根据求解结果来求解极限问题，等等。

四、总结本文介绍了MATLAB插值函数的基本概念，以及MATLAB提供的几种常见的插值函数，包括线性插值、多项式插值、样条插值和指数插值。

这些插值函数的应用及其广泛，可以用来拟合复杂的数据，以及帮助解决一些复杂的数学和工程问题。

样条插值
样条插值是一种分段插值方法，它在每个小区间上使用低 次多项式进行插值，同时保证整个插值函数的连续性和光 滑性。
MATLAB中实现插值法
MATLAB提供的插值函数
MATLAB提供了多种内置函数来实现不同类型的插值，如`interp1`、`interp2`、`interp3` 等，分别用于一维、二维和三维数据的插值。
03
二维数据插值方法
网格数据插值
线性插值
基于已知网格点上的数据，通过 线性插值方法计算未知点的值。 这种方法简单快速，但可能不够 精确。
双三次插值
使用周围的16个网格点上的数据 ，构建一个双三次多项式来逼近 未知点的值。这种方法比线性插 值更精确，但计算量较大。
散点数据插值
最近邻插值
将未知点的值设置为距离其最近的已知点的值。这种方法简 单快速，但可能导致不连续的结果。
信号调制与解调中应用
信号调制
在通信系统中，插值法可用于实现信号的调制处理，将基带信号 转换为适合在信道中传输的已调信号。
信号解调
接收端在接收到已调信号后，可以使用插值法对信号进行解调处理 ，还原出原始的基带信号。
符号同步与定时恢复
在数字通信系统中，插值法可用于实现符号同步和定时恢复，确保 接收端能够准确地提取出传输的符号信息。
07
总结与展望
回顾本次课程重点内容
插值法基本概念
插值法是一种通过已知数据点估算未知数据点的方法，广泛应用于 数据分析和科学计算领域。
MATLAB插值法实现
通过MATLAB提供的插值函数，如`interp1`、`interp2`、`interp3` 等，实现一维、二维和三维数据的插值计算。
插值法应用场景
图像修复与增强中应用

matlab插值函数用法在MATLAB 中，插值函数用于根据已知数据点的值，估计在这些数据点之间的位置的值。

MATLAB 提供了多种插值函数，常用的包括`interp1`、`interp2`、`interp3` 等。

下面是一些常见的MATLAB 插值函数的用法：1. interp1：一维插值函数，用于对一维数据进行插值。

```matlab% 创建一些示例数据x = 1:5;y = [3 7 2 5 8];% 定义插值点xi = 1:0.1:5;% 进行线性插值yi = interp1(x, y, xi, 'linear');```2. interp2：二维插值函数，用于对二维数据进行插值。

```matlab% 创建一些示例数据[X, Y] = meshgrid(1:5, 1:5);Z = peaks(5);% 定义插值点[XI, YI] = meshgrid(1:0.1:5, 1:0.1:5);% 进行二维插值ZI = interp2(X, Y, Z, XI, YI, 'linear');```3. interp3：三维插值函数，用于对三维数据进行插值。

```matlab% 创建一些示例数据[X, Y, Z] = meshgrid(1:5, 1:5, 1:5);V = rand(5, 5, 5);% 定义插值点[XI, YI, ZI] = meshgrid(1:0.1:5, 1:0.1:5, 1:0.1:5);% 进行三维插值VI = interp3(X, Y, Z, V, XI, YI, ZI, 'linear');```这些函数中的`'linear'` 参数表示使用线性插值方法，你也可以选择其他插值方法，比如`'nearest'`、`'spline'` 等。

此外，还可以根据需要进行更高级的插值操作，比如多项式插值、样条插值等。

hours=1:12; temps=[5 8 9 15 25 29 31 30 22 25 27 24]; h=1:0.1:12; t1=interp1(hours,temps,h,'spline'); %(直接输出数据将是很多的) t2=interp1(hours,temps,h, 'nearest'); t3=interp1(hours,temps,h, 'linear'); t4=interp1(hours,temps,h, 'cubic'); subplot(2,2,1); plot(hours,temps, ' bo',h,t1, 'r'); title('spline '); %作图 subplot(2,2,2); plot(hours,temps, 'bo',h,t2, 'r'); title(' nearest'); subplot(2,2,3); plot(hours,temps, 'bo',h,t3, 'r'); title('linear'); subplot(2,2,4); plot(hours,temps, 'bo',h,t4, 'r', h,t1, 'g'); title('cubic-spline') 3
4
用MATLAB作散点数据的插值计算
插值函数griddata格式为:
cz =griddata（x，y，z，cx，cy，‘method’） 被插值点 的函数值
插值 节点 被插值点 插值方法
‘nearest’ 最邻近插值 ‘linear’ 双线性插值 ‘cubic’ 双三次插值 'v4'- Matlab提供的插值方法 缺省时, 双线性插值

线性插值
通过两点之间的直线进行插值， 计算简单但精度较低。
非线性插值
使用非直线函数进行插值，如 多项式、样条函数等，精度较
高但计算复杂度也较高。
02
Matlab插值函数
interp1函数
总结词
一维数据插值函数
详细描述
interp1函数用于在一维数据上进行插值。它接受两个参数：x和y，分别表示数 据点的x坐标和y坐标。通过指定新的x坐标，可以计算出对应的y坐标，从而实 现插值。
要点二
详细描述
多维线性插值的基本思想是通过已知点之间的线性关系来 估计未知点的值。在多维空间中，可以使用多个线性方程 来表示已知点之间的关系，然后解这些方程来得到未知点 的估计值。
多维多项式插值
总结词
多项式插值是一种常用的数据插值方法，适用于一维数 据的插值。在多维数据插值中，可以使用多维多项式插 值来估计未知点的值。
多重二次插值
在多个维度上进行二次插 值，适用于各维度间关系 较复杂的情况。
多重样条插值
在多个维度上进行样条插 值，适用于需要平滑估计 的情况。
实际应用中的插值案例
时间序列数据插值
在金融、经济等领域，时间序列数据经常需要进行插值以填补缺 失值。
图像处理中的插值
在图像缩放、旋转等操作中，需要进行插值以平滑图像。
线性插值
通过已知的点对，使用线性函数进行插值，适用 于数据点分布较均匀的情况。
二次插值
使用二次函数进行插值，适用于已知三个或更多 数据点的情况，能够提供更精确的估计。
三次样条插值
通过构建三次样条函数进行插值，适用于需要平 滑插值的情况。
多维数据插值的案例
多元线性插值
在多个维度上进行线性插 值，适用于各维度间关系 较简单的情况。

灰度级插值之双线性原理与实现（陈云川********************,CD）1 原理简述在对图像进行空间变换的过程中，典型的情况是在对图像进行放大处理的时候，图像会出现失真的现象。

这是由于在变换之后的图像中，存在着一些变换之前的图像中没有的像素位置。

为了说明这个问题，不妨假设有一副大小为64x64的灰度图像A，现在将图像放大到256x256，不妨令其为图像B，如图1所示。

显然，根据简单的几何换算关系，可以知道B图像中(x,y)处的像素值应该对应着A图像中的(x/4,y/4)处的象素值，即B(x,y) = A(x/4,y/4) （式1）对于B中的(4,4),(4,8),(4,16)…(256,256)这些位置，通过式1就可以计算出其在A 中的位置，从而可以得到灰度值。

但是，对于B中的(1,1),(1,2),(1,3)…等等这些坐标点而言，如果按照式1计算的话，那么它们在A中对应的坐标不再是整数。

比如，对于B中的坐标点(1,1)，其在A中的对应坐标就变成了(0.25,0.25)。

对于数字图像而言，小数坐标是没有意义的。

因此，必须考虑采用某种方法来得到B中像素点在A中对应位置上的灰度级。

处理这一问题的方法被称为图像灰度级插值。

常用的插值方式有三种：最近邻域插值、双线性插值、双三次插值。

理论上来讲，最近邻域插值的效果最差，双三次插值的效果最好，双线性插值的效果介于两者之间。

不过对于要求不是非常严格的图像插值而言，使用双线性插值通常就足够了。

本文中将采用matlab实现一个双线性插值的程序。

双线性插值的原理如图2所示。

图像之间坐标映射有两种方式：如果是从原图像的坐标映射到目标图像，称为前向映射，反之则称为后向映射。

显然，双线性插值采用的是后向映射方式。

下面对图2的具体含义进行说明。

首先，根据几何关系，从B图像中的坐标(x,y)得到A图像中的坐标(x/4,y/4)，但是，映射得到的这个坐标(x/4,y/4)并没有刚好位于A 图像中的整数坐标上，而是映射到了四个像素坐标(a,b)、(a+1,b)、(a,b+1)、(a+1,b+1)所围成的矩形之间，其中，a、b是A图像的整数坐标。

基于Matlab的双线性插值算法在图像旋转中的应用
曹佃国;陈浩杰;李鹏
【期刊名称】《中国印刷与包装研究》
【年(卷),期】2010(002)004
【摘要】插值运算作为一种标准的运算方法在图像处理领域,尤其是在图像的放大、旋转和卷积处理过程中有着广泛的应用.本文提出了一种新的双线性插值算法,通过
对超出图像边界的区域进行取模操作,实现图像阵的循环.采用Matlab编程实现该
算法,并应用到图像旋转中.实验证明,用该算法旋转图像时,在特定角度(90.、180.和270.)可以完整显示原始图像;任意角度旋转时,可以看到超出图像范围的像素部分自动进入了斜线对侧,较好地显示出图像旋转的边界变化和旋转位置的循环.
【总页数】5页(P74-78)
【作者】曹佃国;陈浩杰;李鹏
【作者单位】曲阜师范大学印刷学院,日照,276826;曲阜师范大学印刷学院,日
照,276826;山东大学,控制科学与工程学院,济南,250061
【正文语种】中文
【中图分类】TP391.41
【相关文献】
1.插值算法在图像旋转中的应用 [J], 郝蕊洁;万小红
2.H.26L中基于双线性和立方卷积的混合插值算法 [J], 曹宁;孙宇;胡琳娜
3.双线性插值算法在荔枝树光合模拟中叶片图像旋转中的应用 [J], 李震;洪添胜;吴
伟斌;张文昭;郭灼
4.基于MATLAB的多种插值算法在地表时序监测中的应用研究 [J], 郭瑞;李素敏;陈娅男
5.基于DSP的双线性插值算法在图像旋转中的应用 [J], 尹雪; 刘思念; 袁春梅; 周杰
因版权原因，仅展示原文概要，查看原文内容请购买。

matlab练习程序（向量插值）有两个向量，我们想从起始向量平滑的过度到终⽌向量，那么中间的向量就可以通过插值的⽅式得到。

这在图形学中图形旋转或者机器⼈中物体姿态旋转都可以⽤到。

有三种⽅法：Lerp，NLerp和SLerp。

Lerp为线性插值，公式如下：NLerp为线性插值后归⼀化，公式如下：SLerp为球⾯插值，公式如下：公式中的v0和v1就在起始与结束向量，换成四元数同理。

t为插值的中间值，球⾯插值中theta为两个向量间的夹⾓。

实现代码如下：clear all;close all;clc;v1=[123]; %起始向量v2=[4 -5 -6]; %终⽌向量%转为单位向量nv1 = v1/norm(v1);nv2 = v2/norm(v2);%画出起始终⽌向量quiver3(0,0,0,nv1(1),nv1(2),nv1(3));hold on;quiver3(0,0,0,nv2(1),nv2(2),nv2(3));%起始终⽌向量转为四元数x = nv1(1);y=nv1(2);z=nv1(3);q1 = angle2quat(x,y,z);x = nv2(1);y=nv2(2);z=nv2(3);q2 = angle2quat(x,y,z);%计算向量夹⾓w = acos(sum(nv1.*nv2));figure;%四元数插值for t=0:0.1:1q = sin((1-t)*w)/sin(w)*q1 + sin(t*w)/sin(w)*q2; %球⾯插值 slerp% q = (1-t)*q1 + t*q2; %⼀般插值 lerp% q = q/norm(q); %⼀般插值归⼀化 nlerp[x,y,z] = quat2angle(q);l=[x y z];x = x/norm(l);y = y/norm(l);z = z/norm(l);quiver3(0,0,0,x,y,z);hold on;endfigure;%向量插值for t=0:0.1:1q = sin((1-t)*w)/sin(w)*nv1 + sin(t*w)/sin(w)*nv2; %球⾯插值 slerp% q = (1-t)*nv1 + t*nv2; %⼀般插值 lerp% q = q/norm(q); %⼀般插值归⼀化 nlerpquiver3(0,0,0,q(1),q(2),q(3));hold on;end结果如下：初始两个向量：四元数球⾯插值：向量球⾯插值：向量直接插值：从效果上看，向量球⾯插值应该是最好的，向量直接插值在转动⾓较⼤的时候⽆法均匀插值。

m a t l a b旋转实现(最近邻值-双线性-三次卷积插值实现插值)对图像进行旋转，使用最近邻插值法，双线性插值，三次卷积插值三种方法进行插值。

源码：clc;clear all;close all;Img=imread('test1.bmp');Img=double(Img);[h w]=size(Img);alpha=pi/6; %逆时针旋转的角度wnew=w*cos(alpha)+h*sin(alpha); %新图像的宽widthhnew=w*sin(alpha)+h*cos(alpha); %新图像的高heighthwnew=ceil(wnew); %取整hnew=ceil(hnew);u0=w*sin(alpha); %平移量T=[cos(alpha),sin(alpha);-sin(alpha),cos(alpha)]; %变换矩阵Imgnew1=zeros(hnew,wnew);Imgnew2=zeros(hnew,wnew);Imgnew3=zeros(hnew,wnew);for u=1:hnew %u和v是新图像坐标，变换到原图像坐标x和y中。

for v=1:wnewtem=T*([u;v]-[u0;0]);x=tem(1);y=tem(2);if x>=1 & x<=h & y>=1 & y<=w %若变换出的x和y在原图像范围内x_low=floor(x);x_up=ceil(x);y_low=floor(y);y_up=ceil(y);if (x-x_low)<=(x_up-x) %采用最近点法，选取距离最近点的像素赋给新图像x=x_low;elsex=x_up;endif (y-y_low)<=(y_up-y)y=y_low;elsey=y_up;endp1=Img(x_low,y_low); %双线性插值，p1到p4是（x,y）周围的四个点 p2=Img(x_up,y_low);p3=Img(x_low,y_low);p4=Img(x_up,y_up);s=x-x_low;t=y-y_low;Imgnew1(u,v)=Img(x,y);Imgnew2(u,v)=(1-s)*(1-t)*p1+(1-s)*t*p3+(1-t)*s*p2+s*t*p4;endif x>=2 & x<=h-2 & y>=2 & y<=w-2 %若变换出的x和y在原图像范围内 x_1=floor(x)-1;x_2=floor(x);x_3=floor(x)+1;x_4=floor(x)+2;y_1=floor(y)-1;y_2=floor(y);y_3=floor(y)+1;y_4=floor(y)+2;A=[sw(1+x-x_2),sw(x-x_2),sw(1-(x-x_2)),sw(2-(x-x_2))];C=[sw(1+y-y_2),sw(y-y_2),sw(1-(y-y_2)),sw(2-(y-y_2))];B=[ Img(x_1,y_1),Img(x_1,y_2),Img(x_1,y_3),Img(x_1,y_4);Img(x_2,y_1),Img(x_2,y_2),Img(x_2,y_3),Img(x_2,y_4);Img(x_3,y_1),Img(x_3,y_2),Img(x_3,y_3),Img(x_3,y_4);Img(x_4,y_1),Img(x_4,y_2),Img(x_4,y_3),Img(x_4,y_4)];Imgnew3(u,v)=A*B*C';endendendsubplot(2,2,1),imshow(Img,[]),title('原图');subplot(2,2,2),imshow(Imgnew1,[]),title('最近邻插值法'); subplot(2,2,3),imshow(Imgnew2,[]),title('双线性插值法'); subplot(2,2,4),imshow(Imgnew3,[]),title('三次卷积插值法');。