matlab旋转实现(最近邻值,双线性,三次卷积插值实现插值)
- 格式:docx
- 大小:413.25 KB
- 文档页数:3

题 7:一维函数插值算法课题内容:课题 7:一维函数插值算法课题内容:对函数||e-y x=,取[-5,5]之间步长为 1 的值*10作为粗值,以步长0.1 作为细值,编写程序实现插值算法:最邻近插值算法,线性插值算法和三次多项式函数插值算法,并对比插值效果。
课题要求:1、设计良好的人机交互 GUI 界面。
2、自己编写实现插值算法。
3、在同一个图形窗口显示对比最后的插值效果。
附录一、界面设计二、图像结果三、程序设计1、线性插值function pushbutton1_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f1=[];for x1=-5:0.1:5a=(x1-floor(x1));%请读者认真逐一带入推导if x1==floor(x1)f1=[f1,y(floor(x1)+6)];elsef1=[f1,y(floor(x1)+6)+a*(y(floor(x1)+7)-y(floor(x1)+6))]; endendm=-5:0.1:5plot(m,f1,'-r',x,y,'+')axis([-5 5 0 10])legend('liner插值','原函数');xlabel('X');ylabel('Y');title('liner插值与原函数的对比');grid2、多项式插值x0=-5:1:-3;y0=10*exp(-abs(x0));x=-5:0.1:-3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-3:1:-1;y0=10*exp(-abs(x0));x=-3:0.1:-1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-1:1:1;y0=10*exp(-abs(x0));x=-1:0.1:1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=1:1:3;y0=10*exp(-abs(x0));x=1:0.1:3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=3:1:5;y0=10*exp(-abs(x0));x=3:0.1:5;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');grid3、最邻近插值function pushbutton3_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f2=[];for x1=-5:0.1:5if abs(x1-floor(x1))<0.5f2=[f2,y(floor(x1)+6)];elsef2=[f2,y(floor(x1)+7)];endendm=[-5:0.1:5];f4=10*exp(-abs(m));plot(m,f2,'-r',x,y,'+')axis([-5 5 0 10])legend('nearest插值','原函数');xlabel('X');ylabel('Y');title('nearest插值与原函数的对比');grid。


matlab曲线插值方法摘要:一、引言1.MATLAB曲线插值方法背景介绍2.文章目的与意义二、MATLAB曲线插值方法分类1.线性插值2.二次多项式插值3.三次样条插值4.三次贝塞尔插值5.三次Hermite插值三、线性插值1.原理介绍2.示例代码及结果四、二次多项式插值1.原理介绍2.示例代码及结果五、三次样条插值1.原理介绍2.示例代码及结果六、三次贝塞尔插值1.原理介绍2.示例代码及结果七、三次Hermite插值1.原理介绍2.示例代码及结果八、比较与选择1.各种插值方法优缺点分析2.应用场景选择建议九、结论1.文章总结2.对未来研究的展望正文:matlab曲线插值方法在MATLAB中,曲线插值是一种常见的数据处理和可视化方法。
它可以将离散的数据点连接成平滑的曲线,以便于分析和理解数据。
本文将介绍MATLAB中几种常见的曲线插值方法,包括线性插值、二次多项式插值、三次样条插值、三次贝塞尔插值和三次Hermite插值。
同时,我们将通过示例代码和结果展示这些插值方法的实现过程,并对各种插值方法进行比较和选择,以提供实际应用中的指导。
一、引言MATLAB作为一种广泛应用于科学计算和工程领域的编程语言,其强大的绘图功能为研究人员提供了便利。
在许多应用场景中,需要将离散的数据点连接成平滑的曲线,以直观地表现数据的变化规律。
曲线插值方法正是为了解决这一问题而提出的。
接下来,我们将介绍MATLAB中几种常见的曲线插值方法。
二、MATLAB曲线插值方法分类1.线性插值线性插值是一种简单的插值方法,它通过连接数据点形成一条直线。
在MATLAB中,可以使用`polyfit`函数进行线性插值。
```matlabx = [1, 2, 3, 4];y = [2, 4, 6, 8];p = polyfit(x, y, 1);```2.二次多项式插值二次多项式插值使用一个二次方程来拟合数据点。
在MATLAB中,可以使用`polyfit`函数进行二次多项式插值。

文章标题:深度解析Matlab三次样条插值1. 前言在数学和工程领域中,插值是一种常见的数值分析技术,它可以用来估计不连续数据点之间的值。
而三次样条插值作为一种常用的插值方法,在Matlab中有着广泛的应用。
本文将从简单到复杂,由浅入深地解析Matlab中的三次样条插值方法,以便读者更深入地理解这一技术。
2. 三次样条插值概述三次样条插值是一种利用分段三次多项式对数据点进行插值的方法。
在Matlab中,可以使用spline函数来进行三次样条插值。
该函数需要输入数据点的x和y坐标,然后可以根据需要进行插值操作。
3. 三次样条插值的基本原理在进行三次样条插值时,首先需要对数据点进行分段处理,然后在每个分段上构造出一个三次多项式函数。
这些多项式函数需要满足一定的插值条件,如在数据点处函数值相等、一阶导数相等等。
通过这些条件,可以得到一个关于数据点的插值函数。
4. Matlab中的三次样条插值实现在Matlab中,可以使用spline函数来进行三次样条插值。
通过传入数据点的x和y坐标,可以得到一个关于x的插值函数。
spline函数也支持在已知插值函数上进行插值点的求值,这为用户提供了极大的灵活性。
5. 三次样条插值的适用范围和局限性虽然三次样条插值在许多情况下都能够得到较好的插值效果,但也存在一些局限性。
在数据点分布不均匀或有较大噪音的情况下,三次样条插值可能会出现较大的误差。
在实际应用中,需要根据具体情况选择合适的插值方法。
6. 个人观点和总结通过对Matlab中三次样条插值的深度解析,我深刻地理解了这一插值方法的原理和实现方式。
在实际工程应用中,我会根据数据点的情况选择合适的插值方法,以确保得到准确且可靠的结果。
我也意识到插值方法的局限性,这为我在实际工作中的决策提供了重要的参考。
通过以上深度解析,相信读者已经对Matlab中的三次样条插值有了更加全面、深刻和灵活的理解。
在实际应用中,希望读者能够根据具体情况选择合适的插值方法,以提高工作效率和准确性。

MATLAB技术图像插值方法引言在现代数字图像处理领域中,图像插值是一项重要的技术。
插值方法用于增加由离散数值组成的图像的分辨率和细节,以提高图像的质量。
MATLAB作为一种强大的数值计算和图像处理工具,提供了多种图像插值方法,本文将介绍其中几种常用的方法以及其应用。
1. 双线性插值法双线性插值法是一种简单而常用的插值方法。
该方法通过在目标像素周围的四个相邻像素之间进行线性插值来估计目标像素的灰度值。
具体而言,假设目标像素位于离散坐标(x,y)处,其周围四个像素为P1(x1,y1),P2(x2,y2),P3(x1,y2),P4(x2,y1),则目标像素的灰度值可以通过以下公式计算得到:I(x,y) = (1-dx)(1-dy)I(P1) + dx(1-dy)I(P2) + (1-dx)dyI(P3) + dxdyI(P4)其中,dx = x-x1,dy = y-y1。
双线性插值法的优点在于简单,计算效率高,但其结果对于曲线边缘可能会产生模糊的效果。
2. 双三次插值法双三次插值法是一种更高级的插值方法,它通过在目标像素周围的16个相邻像素之间进行三次样条插值来估计目标像素的灰度值。
具体而言,假设目标像素位于离散坐标(x,y)处,其周围16个像素为Pn,其中n=1,2,...,16,那么目标像素的灰度值可以通过以下公式计算得到:I(x,y) = ∑wi(x,y)I(Pi)其中,wi(x,y)是插值权重,Pi是第i个相邻像素的灰度值。
双三次插值法的优点在于能够更好地保持图像的细节和边缘信息,并且结果较为平滑。
但由于计算量较大,相对于双线性插值法,它的速度较慢。
3. 基于卷积核的插值法除了双线性插值法和双三次插值法之外,MATLAB还提供了基于卷积核的插值方法,如图像放大中的“拉普拉斯金字塔”算法。
这种方法采用了金字塔结构,将原始图像不断降采样生成多层金字塔,然后根据不同的插值需求选择相应层级的低分辨率图像,并根据图像金字塔层级进行插值处理。

Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法,MATLAB提供的插值方法有几种: 'method'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'cubic'立方插值.缺省时表示线性插值注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
例如:在一天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度.x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为: 27.8725若要得到一天24小时的温度曲线,则:xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi是阶数为length(xi)*size(Y,2)的输出矩阵。
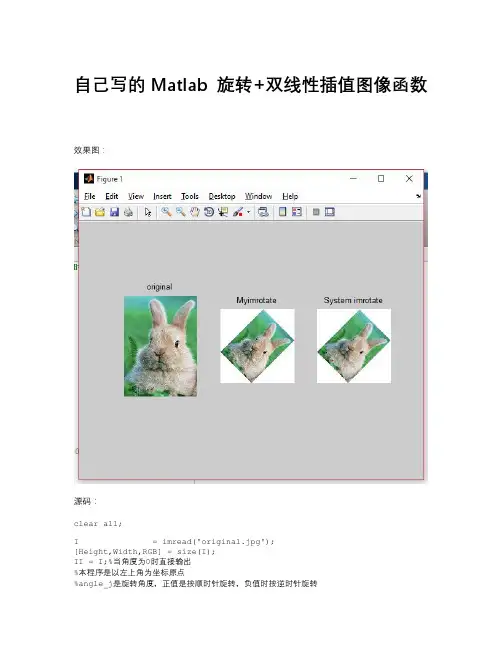
自己写的Matlab 旋转+双线性插值图像函数效果图:源码:clear all;I = imread('original.jpg');[Height,Width,RGB] = size(I);II = I;%当角度为0时直接输出%本程序是以左上角为坐标原点%angle_j是旋转角度,正值是按顺时针旋转,负值时按逆时针旋转angle_j = 181;%angle是弧度angle = 2*pi*angle_j/360;%将angle转成正值while(angle < 0)angle = 2 * pi + angle;end%约束在0-2π内while(angle > 2 * pi)angle = angle - 2 * pi;end%tag是判断下面的while循环有没有执行过tag = 0;while(angle > 0)%超过90度的旋转,都先旋转90度,直到角度在0°-90°之间%原理是旋转90度整数倍时,信息是不丢失的if angle >= pi/2a = pi/2;angle = angle - pi/2;elseif 0 < angle < pi/2a = angle;angle = 0;endif tag == 0tag = 1;elseI = II;[Height,Width,RGB] = size(I);%在旋转后的图像上继续旋转,从而实现大于90°的旋转end%正向变换用sina = sin(a);cosa = cos(a);%逆向变换用_m == _minussina_m = sin(-a);cosa_m = cos(-a);%旋转后图像的长度和宽度II_height = round(sina * Width + cosa * Height);II_width = round(sina * Height + cosa * Width);II = ones(II_height,II_width,3);%先转成unit8。


matlab三次样条插值的方法Cubic spline interpolation is a common method used in MATLAB to approximate values between specified data points. This technique involves fitting a piecewise cubic polynomial to the data points, ensuring that the function is smooth and continuous at the knots. Through this process, the spline curve can accurately represent the overall trend of the data, making it particularly useful in various scientific and engineering applications.三次样条插值是MATLAB中常用的一种方法,用于在指定数据点之间近似数值。
这种技术涉及将分段三次多项式拟合到数据点,确保在节点处函数平滑连续。
通过这个过程,样条曲线可以准确地表示数据的总体趋势,使其特别适用于各种科学和工程应用。
One advantage of cubic spline interpolation is its ability to capture the local behavior of the data while maintaining global smoothness. This is achieved by constructing individual cubic polynomials between adjacent data points, ensuring that the interpolated curve passes through each data point without introducing significant oscillations or deviations. As a result, cubic splines provide a reliableand visually appealing way to interpolate data that may exhibit complex patterns or fluctuations.三次样条插值的一个优点是能够捕捉数据的局部行为,同时保持全局的平滑性。

实验三图像的几何操作一、图像的基本运算1、加法运算图像相加一般用于对同一场景的多幅图像求平均效果,以便有效地降低具有叠加性质的随机噪声。
直接采集的图像品质一般都较好,不需要进行加法运算处理,但是对于那些经过长距离模拟通信方式传送的图像(如卫星图像),这种处理是必不可少的。
在MA TLAB7.0中,如果要进行两幅图像的加法,或者给一幅图像加上一个常数,可以调用imadd函数来实现。
imadd函数将某一幅输入图像的每一个像素值与另一幅图像相应的像素值相加,返回相应的像素值之和作为输入图像。
imadd函数的调用格式可参考图像处理的工具箱。
下面的程序可将图1两幅图像叠加在一起,叠加效果如图2所示。
imshow('rice.png');imshow('cameraman.tif');I=imread('rice.png');J=imread('cameraman.tif');K=imadd(I,J,'uint16');%大小必须一样imshow(K,[])图1 图2给图像的每一个像素加上一个常数可以使图像的亮度增加。
例如以下程序示例的处理效果如图3所示。
I=imread('rice.png');J=imadd(I,50);subplot(1,2,1),imshow(I);subplot(1,2,2),imshow(J);图32、减法运算图像减法也称为差分方法,是一种常用于检测图像变化及运动物体的图像处理方法。
图像减法可以作为许多图像处理过程的准备步骤。
例如,可以使用图像减法来检测一系列相同场景图像的差异。
图像减法与阈值化处理的综合使用通常是建立机器视觉系统最有效的方法之一。
当然,在利用图像减法处理图像时,往往需要考虑背景的更新机制,尽量补偿因天气、光线等因素对图像显示效果造成的影响。
在MATLAB7.0中,使用imsubtract函数可以将一幅图像从另一幅图像中减去,或者从一幅图像中减去一个常数。

用matlab 实现三次 NURBS 插值曲线 作者:大漠孤狼 发表于matlab 乐园()作者:这是我在大学时做大学生研究计划时写的,当时刚学会matlab ,编写了这个程序,用了很多循环,效率不高.当时我并不清楚循环是matlab 的弱点,等明白了,也不做这方面的工作了,也就懒的去改写了.如果谁需要用,就自己改吧.算法也有一些问题,我就不多说了,自己看吧一 、三次NURBS 插值算法给定平面控制顶点d i (i=1,2,…n)及对应的权因子i ω (i=1,2,…n),可定义一条三次NURBS 曲线。
先对控制顶点进行参数化,得一矢量:U=[u 0,u 1,u 2…,u n+4]则三次NURBS 曲线的分段方程形式为: ∑∑+====33,33,1)()()(k k i i i k k i i i k u N u N d u P ωω u ∈[u k+3,u k+4] k=0,1,2,…,n-3 (1) 首先证明一条性质:若三点d k ,d k+1,d k+2共线,且满足 )()()()(33,2333,233,2333,1++++++++++++=k k k k k k k k k k k k k k k u N u N d u N d u N d ωωωω则三次NURBS 曲线插值点d k+1.证明:由(1)式可得:)()()()()()()(33,2233,1133,233,22133,1133,3+++++++++++++++++++++=k k k k k k k k k k k k k k k k k k k k k k k u N u N u N d u N d u N d u N u P ωωωωωω )()()()()()()(43,3343,2243,11343,23243,22143,114++++++++++++++++++++++++++=k k k k k k k k k k k k k k k k k k k k k k k u N u N u N d u N d u N d u N u P ωωωωωω 由以知可得)()()()()()(33,2233,1133,233,22133,1133,1+++++++++++++++++++++=k k k k k k k k k k k k k k k k k k k k k k u N u N u N d u N d u N d u N d ωωωωωω 故性质得证。
matlab双三次插值函数在MATLAB中,双三次插值函数可以通过使用`interp2`函数来实现。
`interp2`函数可以在二维网格上对数据进行插值,其中包括双三次插值。
下面我将详细介绍如何使用`interp2`函数进行双三次插值。
首先,`interp2`函数的基本语法如下:Vq = interp2(X, Y, V, Xq, Yq, 'spline');其中,`X`和`Y`是原始数据的网格坐标,`V`是原始数据的值,`Xq`和`Yq`是要进行插值的点的坐标,`Vq`是插值得到的值。
在这里,我们使用`spline`选项来指定双三次插值。
接下来,我将通过一个简单的示例来说明如何使用`interp2`函数进行双三次插值。
假设我们有一组原始数据`X`,`Y`和`V`,我们想要在新的坐标点`Xq`和`Yq`上进行双三次插值。
matlab.% 创建原始数据。
[X, Y] = meshgrid(1:5, 1:5);V = peaks(5); % 以peaks函数生成一个简单的二维数据作为示例。
% 创建新的坐标点。
[Xq, Yq] = meshgrid(1:0.1:5, 1:0.1:5); % 创建更密集的坐标点用于插值。
% 进行双三次插值。
Vq = interp2(X, Y, V, Xq, Yq, 'spline');% 可视化插值结果。
surf(Xq, Yq, Vq);在这个示例中,我们首先创建了原始数据`X`,`Y`和`V`,然后创建了新的坐标点`Xq`和`Yq`,并使用`interp2`函数进行双三次插值。
最后,我们通过绘制三维曲面来可视化插值结果。
需要注意的是,`interp2`函数还有其他选项可以用来指定不同的插值方法,比如线性插值、最近邻插值等。
另外,对于不规则的数据点,还可以使用`griddata`函数进行插值操作。
希望这个例子能够帮助你理解在MATLAB中如何使用双三次插值函数。
三次样条插值matlab代码实现三次样条插值是一种常用的插值方法,可以用于曲线拟合和数据逼近。
在Matlab中,可以使用内置函数`interp1`来实现三次样条插值。
下面是一个简单的示例代码,演示了如何在Matlab中实现三次样条插值:matlab.% 创建一些示例数据。
x = 1:5;y = [3 6 5 8 2];% 生成更密集的x值,用于插值。
xi = 1:0.1:5;% 使用interp1进行三次样条插值。
yi = interp1(x, y, xi, 'spline');% 绘制原始数据和插值结果。
plot(x, y, 'o', xi, yi, '-');legend('原始数据', '三次样条插值');在这个示例中,我们首先创建了一些示例数据`x`和`y`,然后生成了更密集的`xi`值,用于插值。
接下来,我们使用`interp1`函数进行三次样条插值,并将结果存储在`yi`中。
最后,我们使用`plot`函数将原始数据和插值结果可视化出来。
需要注意的是,`interp1`函数中的第四个参数'spline'表示我们使用三次样条插值方法。
除了'spline'外,还可以选择'linear'(线性插值)或'pchip'(分段立方插值)等方法,具体选择取决于实际情况和数据特点。
以上就是在Matlab中实现三次样条插值的简单示例代码。
当然,实际应用中可能涉及到更复杂的数据和情况,需要根据具体问题进行相应的调整和处理。
希望这个示例能够帮助到你理解如何在Matlab中实现三次样条插值。
matlab插值类型在MATLAB中,插值是一种常用的数据处理技术,用于估计在已知数据点之间的数值。
MATLAB提供了多种插值方法,每种方法都有其适用的情况和特点。
以下是一些常见的插值类型:1. 线性插值(linear interpolation),线性插值是一种简单的插值方法,通过已知数据点之间的直线来估计新的数据点。
在MATLAB中,可以使用interp1函数来进行线性插值。
2. 三次样条插值(cubic spline interpolation),三次样条插值是一种平滑的插值方法,它利用已知数据点之间的三次多项式来估计新的数据点。
在MATLAB中,可以使用interp1函数并指定'cubic'选项来进行三次样条插值。
3. 最近邻插值(nearest neighbor interpolation),最近邻插值是一种简单的插值方法,它通过找到最接近新数据点的已知数据点来进行估计。
在MATLAB中,可以使用interp1函数并指定'nearest'选项来进行最近邻插值。
4. 二维插值(2D interpolation),除了在一维数据上进行插值外,MATLAB还提供了在二维数据上进行插值的方法。
可以使用interp2函数来进行二维插值,同样可以选择线性插值、三次样条插值或最近邻插值。
除了上述提到的插值方法,MATLAB还提供了其他一些特定的插值函数,如interpft、interpn等,用于处理不同类型的数据和插值需求。
选择合适的插值方法取决于数据的特点、插值精度的要求以及计算效率等因素。
在实际应用中,需要根据具体情况选择合适的插值方法来进行数据处理和分析。
matlab矩阵旋转任意⾓度的函数imrotate >>帮助 imrotate旋转图像。
B=imrotate(A,ANGLE)在A中按⾓度旋转图像A围绕其中⼼点的逆时针⽅向。
旋转图像顺时针⽅向,为“⾓度”指定负值。
imrotate⽣成输出图像B⼤到⾜以包含整个旋转图像。
imrotate使⽤最近邻插值,设置B中像素的值在旋转后的图像外为0(零)。
B=imrotate(A,⾓度,⽅法)使⽤插值旋转图像A⽅法指定的⽅法。
⽅法是⼀个字符串,它可以具有以下值。
默认值⽤⼤括号({})括起来。
{'nearest'}最近邻插值“双线性”双线性插值“双三次”双三次插值。
注:此插值⽅法可以在原始值之外⽣成像素值范围。
B=imrotate(A,ANGLE,METHOD,BBOX)旋转图像A,其中BBOX指定输出图像B.BBOX的⼤⼩是⼀个⽂本字符串,可以以下值之⼀。
默认值⽤⼤括号括起来({}).{'loose'}使输出图像B⾜够⼤以包含整个旋转图像。
B⼀般⽐A⼤。
“裁剪”使输出图像B的⼤⼩与输⼊图像相同A、裁剪旋转图像以适应。
Class⽀持-------------输⼊图像可以是数字图像或逻辑图像。
输出图像是与输⼊图像相同的类。
注意----函数imrotate在版本9.3(R2015b)中发⽣了更改。
上⼀个图像处理⼯具箱的版本使⽤不同的空间习俗。
如果你需要同样的结果实现时,使⽤函数IMROTATE\u OLD。
此函数可以利⽤数据类型的硬件优化uint8,uint16,single和double可以跑得更快。
例⼦-------%这个例⼦通过%将图像旋转-1度。
I=fitsread('太阳光谱.fts');I=材料2射线(I);J=旋转(I,-1,'双线性','裁剪');图,图(I),图,imshow(J)另请参见imrotate_old、imcrop、imresize、imtransform、tformarray。
MATLAB 程序设计期中考查在许多问题中,通常根据实验、观测或经验得到的函数表或离散点上的信息,去研究分析函数的有关特性。
其中插值法是一种最基本的方法,以下给出最基本的插值问题——三次样条插值的基本提法:对插值区间[]b a ,进行划分:b x x x a n ≤<⋯⋯<<≤10,函数()x f y =在节点i x 上的值()()n i x f y i i ⋯⋯==,2,1,0,并且如果函数()x S 在每个小区间[]1,+i i x x 上是三次多项式,于[]b a ,上有二阶连续导数,则称()x S 是[]b a ,上的三次样条函数,如果()x S 在节点i x 上还满足条件()()n i y x S i i ⋯⋯==,1,0则称()x S 为三次样条插值函数。
三次样条插值问题提法:对[]b a ,上给定的数表如下.求一个分段三次多项式函数()x S 满足插值条件()()n i y x S i i ⋯⋯==,1,0 式,并在插值区间[]b a ,上有二阶连续导数。
这就需要推导三次样条插值公式:记()x f '在节点i x 处的值为()i i m x f ='(n i ⋯⋯=,1,0)(这不是给定插值问题数表中的已知值)。
在每个小区间[]1,+i i x x 利用三次Hermite 插值公式,得三次插值公式:()()()()1111+++++++=i i i i i i i i i m m x y x y x x S ββαα,[]1,+∈i i x x x 。
为了得到这个公式需要n 4个条件:(1).非端点处的界点有n 2个;(2).一阶导数连续有1-n 个条件;(3).二阶导数连续有1-n 个条件,其中边界条件:○1()()nn m x S m x S ='=' 00○2()()αα=''=''nx S x S 00 ○3()()()()16500403βααβαα=''+'=''+'n n x S x S x S x S ○4n y y =0 ()()()()000000-''=+''-'=+'nn x S x S x S x S 其中:()⎩⎨⎧=≠=j i j i x j i,1,0α ()0='j i x α ()0=j i x β 且(1,0,=j i )。
对图像进行旋转,使用最近邻插值法,双线性插值,三次卷积插值三种方法进行插值。
源码:clc;clear all;close all;Img=imread('test1.bmp');Img=double(Img);[h w]=size(Img);alpha=pi/6; %逆时针旋转的角度wnew=w*cos(alpha)+h*sin(alpha); %新图像的宽widthhnew=w*sin(alpha)+h*cos(alpha); %新图像的高heighthwnew=ceil(wnew); %取整hnew=ceil(hnew);u0=w*sin(alpha); %平移量T=[cos(alpha),sin(alpha);-sin(alpha),cos(alpha)]; %变换矩阵Imgnew1=zeros(hnew,wnew);Imgnew2=zeros(hnew,wnew);Imgnew3=zeros(hnew,wnew);for u=1:hnew %u和v是新图像坐标,变换到原图像坐标x和y中。
for v=1:wnewtem=T*([u;v]-[u0;0]);x=tem(1);y=tem(2);if x>=1 & x<=h & y>=1 & y<=w %若变换出的x和y在原图像范围内x_low=floor(x);x_up=ceil(x);y_low=floor(y);y_up=ceil(y);if (x-x_low)<=(x_up-x) %采用最近点法,选取距离最近点的像素赋给新图像 x=x_low;elsex=x_up;endif (y-y_low)<=(y_up-y)y=y_low;elsey=y_up;endp1=Img(x_low,y_low); %双线性插值,p1到p4是(x,y)周围的四个点 p2=Img(x_up,y_low);p3=Img(x_low,y_low);p4=Img(x_up,y_up);s=x-x_low;t=y-y_low;Imgnew1(u,v)=Img(x,y);Imgnew2(u,v)=(1-s)*(1-t)*p1+(1-s)*t*p3+(1-t)*s*p2+s*t*p4;endif x>=2 & x<=h-2 & y>=2 & y<=w-2 %若变换出的x和y在原图像范围内x_1=floor(x)-1;x_2=floor(x);x_3=floor(x)+1;x_4=floor(x)+2;y_1=floor(y)-1;y_2=floor(y);y_3=floor(y)+1;y_4=floor(y)+2;A=[sw(1+x-x_2),sw(x-x_2),sw(1-(x-x_2)),sw(2-(x-x_2))];C=[sw(1+y-y_2),sw(y-y_2),sw(1-(y-y_2)),sw(2-(y-y_2))];B=[ Img(x_1,y_1),Img(x_1,y_2),Img(x_1,y_3),Img(x_1,y_4);Img(x_2,y_1),Img(x_2,y_2),Img(x_2,y_3),Img(x_2,y_4);Img(x_3,y_1),Img(x_3,y_2),Img(x_3,y_3),Img(x_3,y_4);Img(x_4,y_1),Img(x_4,y_2),Img(x_4,y_3),Img(x_4,y_4)]; Imgnew3(u,v)=A*B*C';endendendsubplot(2,2,1),imshow(Img,[]),title('原图');subplot(2,2,2),imshow(Imgnew1,[]),title('最近邻插值法'); subplot(2,2,3),imshow(Imgnew2,[]),title('双线性插值法'); subplot(2,2,4),imshow(Imgnew3,[]),title('三次卷积插值法');欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
对图像进行旋转,使用最近邻插值法,双线性插值,三次卷积插值三种方法进行插值。
源码:
clc;clear all;close all;
Img=imread('test1.bmp');
Img=double(Img);
[h w]=size(Img);
alpha=pi/6; %逆时针旋转的角度
wnew=w*cos(alpha)+h*sin(alpha); %新图像的宽width
hnew=w*sin(alpha)+h*cos(alpha); %新图像的高heighth
wnew=ceil(wnew); %取整
hnew=ceil(hnew);
u0=w*sin(alpha); %平移量
T=[cos(alpha),sin(alpha);-sin(alpha),cos(alpha)]; %变换矩阵
Imgnew1=zeros(hnew,wnew);
Imgnew2=zeros(hnew,wnew);
Imgnew3=zeros(hnew,wnew);
for u=1:hnew %u和v是新图像坐标,变换到原图像坐标x和y中。
for v=1:wnew
tem=T*([u;v]-[u0;0]);
x=tem(1);
y=tem(2);
if x>=1 & x<=h & y>=1 & y<=w %若变换出的x和y在原图像范围内
x_low=floor(x);
x_up=ceil(x);
y_low=floor(y);
y_up=ceil(y);
if (x-x_low)<=(x_up-x) %采用最近点法,选取距离最近点的像素赋给新图像x=x_low;
else
x=x_up;
end
if (y-y_low)<=(y_up-y)
y=y_low;
else
y=y_up;
end
p1=Img(x_low,y_low); %双线性插值,p1到p4是(x,y)周围的四个点p2=Img(x_up,y_low);
p3=Img(x_low,y_low);
p4=Img(x_up,y_up);
s=x-x_low;
t=y-y_low;
Imgnew1(u,v)=Img(x,y);
Imgnew2(u,v)=(1-s)*(1-t)*p1+(1-s)*t*p3+(1-t)*s*p2+s*t*p4;
end
if x>=2 & x<=h-2 & y>=2 & y<=w-2 %若变换出的x和y在原图像范围内x_1=floor(x)-1;
x_2=floor(x);
x_3=floor(x)+1;
x_4=floor(x)+2;
y_1=floor(y)-1;
y_2=floor(y);
y_3=floor(y)+1;
y_4=floor(y)+2;
A=[sw(1+x-x_2),sw(x-x_2),sw(1-(x-x_2)),sw(2-(x-x_2))];
C=[sw(1+y-y_2),sw(y-y_2),sw(1-(y-y_2)),sw(2-(y-y_2))];
B=[ Img(x_1,y_1),Img(x_1,y_2),Img(x_1,y_3),Img(x_1,y_4);
Img(x_2,y_1),Img(x_2,y_2),Img(x_2,y_3),Img(x_2,y_4);
Img(x_3,y_1),Img(x_3,y_2),Img(x_3,y_3),Img(x_3,y_4);
Img(x_4,y_1),Img(x_4,y_2),Img(x_4,y_3),Img(x_4,y_4)];
Imgnew3(u,v)=A*B*C';
end
end
end
subplot(2,2,1),imshow(Img,[]),title('原图');
subplot(2,2,2),imshow(Imgnew1,[]),title('最近邻插值法'); subplot(2,2,3),imshow(Imgnew2,[]),title('双线性插值法'); subplot(2,2,4),imshow(Imgnew3,[]),title('三次卷积插值法');。