实验二 控制系统的阶跃响应及稳定性分析

实验二二阶系统阶跃响应一、实验目的（1）了解典型二阶系统模拟电路的构成方法及二级闭环系统的传递函数标准式。

（2）研究二阶闭环系统的结构参数--无阻尼振荡频率ωn、阻尼比ζ对过渡过程的影响。

（3）掌握欠阻尼二阶闭环系统在阶跃信号输入时的动态性能指标Mp、tp、ts的计算。

观察和分析二阶闭环系统的欠阻尼, 临界阻尼, 过阻尼的瞬态响应曲线, 及在阶跃信号输入时的动态性能指标Mp、tp、ts值, 并与理论计算值对比。

二、实验设备（1）XMN-2型学习机；（2）CAE-USE辅助实验系统（3）万用表（4）计算机三、实验内容本实验用于观察和分析二阶系统瞬态响应的稳定性。

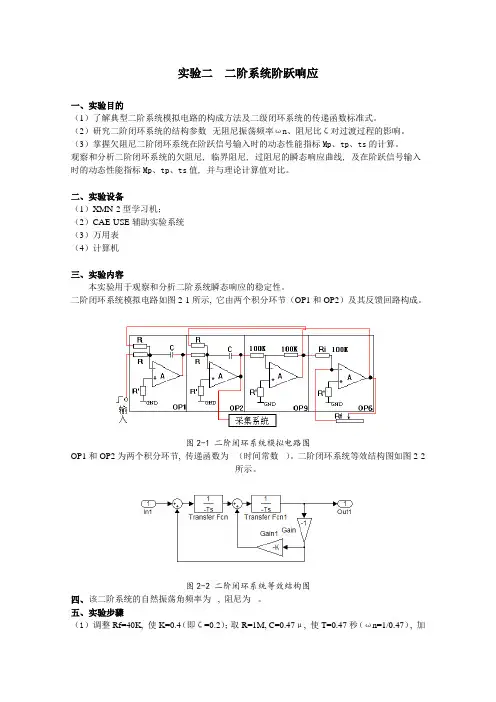
二阶闭环系统模拟电路如图2-1所示, 它由两个积分环节（OP1和OP2）及其反馈回路构成。

图2-1 二阶闭环系统模拟电路图OP1和OP2为两个积分环节, 传递函数为（时间常数）。

二阶闭环系统等效结构图如图2-2所示。

图2-2 二阶闭环系统等效结构图四、该二阶系统的自然振荡角频率为, 阻尼为。

五、实验步骤（1）调整Rf=40K, 使K=0.4（即ζ=0.2）；取R=1M, C=0.47μ, 使T=0.47秒（ωn=1/0.47）, 加入阶跃输入信号x(t)=1V, 记录阶跃响应曲线①；（2）保持ζ=0.2不变, 阶跃信号不变, 取R=1M, C=1.47μ, 使T=1.47秒（ωn=1/1.47）, 记录阶跃响应曲线②；（3）保持ζ=0.2不变, 阶跃信号不变, 取R=1M, C=1μ, 使T=1秒（ωn=1/1）, 记录阶跃响应曲线③；保持ωn=1/0.1不变、阶跃扰动不变, 调整Rf=200K, 使K=2（即ζ=1）, 记录阶跃响应曲线④；保持ωn=1/0.1不变、阶跃扰动不变, 调整Rf=300K, 使K=3（即ζ=1.5）, 记录阶跃响应曲线⑤。

六、数据采集及处理七、实验报告1、推导模拟电路的闭环传递函数Y(s)/X(s)？确定R、C.Rf、Ri与自然振荡角频率和阻尼比之间的关系。

实验室二二阶系统的阶跃响应及稳定性分析实验一．实验目的1.熟悉二阶模拟系统的组成。

2.研究二阶系统分别工作在等几种状态下的阶跃响应。

3.学习掌握动态性能指标的测试方法，研究典型系统参数对系统动态性能和稳定性的影响。

二，实验内容1.ZY17AutoC12BB自动控制原理实验箱。

2.双踪低频慢扫示波器。

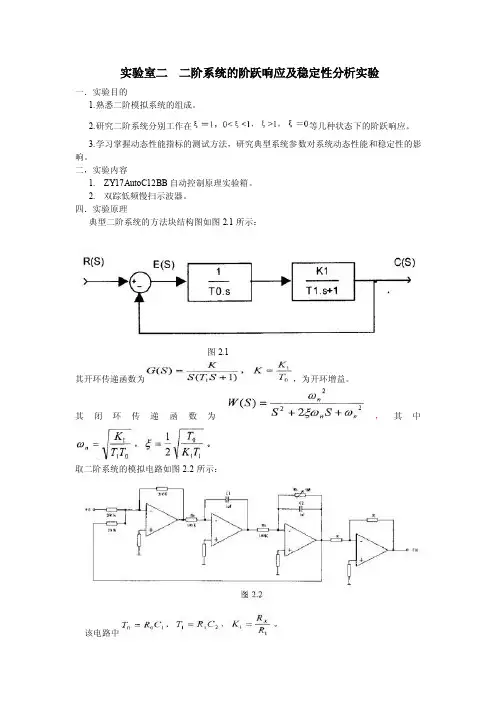
四．实验原理典型二阶系统的方法块结构图如图2.1所示：图2.1其开环传递函数为，为开环增益。

其闭环传递函数为，其中取二阶系统的模拟电路如图2.2所示：该电路中该二阶系统的阶跃响应如图所示：图2.3.1，2.3.2，2.3.3，2.3.4和2.3.5分别对应二阶系统在过阻尼，临界阻尼，欠阻尼，不等幅阻尼振荡（接近于0）和零阻尼（=0）几种状态下的阶跃响应曲线。

改变元件参数Rx大小，可研究不同参数特征下的时域响应。

当Rx为50k时，二阶系统工作在临界阻尼状态;当Rx<50K时，二阶系统工作在过阻尼状态;当Rx>50K时，二阶系统工作在欠阻尼状态;当Rx继续增大时，趋近于零，二阶系统输出表现为不等幅阻尼振荡；当=0时，二阶系统的阻尼为零，输出表现为等幅振荡（因导线均有电阻值，各种损耗总是存在的，实际系统的阻尼比不可能为零）。

五. 实验步骤1.利用实验仪器，按照实验原理设计并连接由一个积分环节和一个惯性环节组成的二阶闭环系统的模拟电路。

此实验可使用运放单元（一），（二），（三），（五）及元器件单元中的可调电阻。

（1）同时按下电源单元中的按键开关S001，S002，再按下S003，调节可调电位器W001,使T006（-12V—+12V）输出电压为+1V，形成单位阶跃信号电路，然后将S001,S002再次按下关闭电源。

（2）按照图2.2连接好电路，按下电路中所用到运放单元的按键开关。

（3）用导线将连接好的模拟电路的输入端于T006相连接，电路的输出端与示波器相连接。

（4）同时按下按键开关S001,S002时，利用示波器观测该二阶系统模拟电路的阶跃特性曲线，并由实验测出响应的超调量和调节时间，将结果记录下来。

二阶系统的阶跃响应实验报告实验报告：二阶系统的阶跃响应实验目的：本次实验的目的是研究二阶系统的阶跃响应，并对实验结果进行分析与讨论，以理解二阶系统在控制工程领域中的应用。

实验原理：二阶系统是指具有二阶特性的系统，即在系统受到激励信号后，系统的响应随时间的变化呈现出一定的规律。

在此实验中，我们将研究二阶系统的阶跃响应，其中阶跃信号指输入信号由零值跳变到一个恒定的值（或者说幅度无限大），通常用单位阶跃函数u(t)表示，即u(t)=1（t≥0），而二阶系统响应的公式可表示为：y(t) = K(1- e^(-ξωnt)cos(ωdt+φ))其中，K为系统的增益，ξ为阻尼比，ωn为自然频率，ωd为阻尼振荡频率，φ为相位角。

实验步骤：1. 确定实验装置的参数，并将之记录下来，包括：二阶系统的增益K、阻尼比ξ、自然频率ωn，以及阶跃信号的幅值u0等。

2. 将二阶系统的输入信号设置为阶跃信号u(t)，并将输出信号y(t)记录下来，同时进行数据采集和记录。

3. 根据数据得出实验结果，并利用软件对实验数据进行处理和分析，包括波形比较、响应曲线分析和幅值与相位移测量等。

实验结果：在此次实验中，我们得到了如下的实验参数：增益K = 1.5V阻尼比ξ = 0.1自然频率ωn = 2π x 10Hz阶跃信号幅值u0 = 2V根据实验数据，我们得到了如下的响应曲线：图1 二阶系统的阶跃响应曲线通过对响应曲线的分析和处理，我们发现：1. 二阶系统的阶跃响应具有一定的超调和振荡特性，表明系统的稳定性较差，需要进行进一步的优化和调整。

2. 阻尼比ξ的大小与系统的响应有着密切的关系，通常应根据系统的具体情况进行合理的选择和调整，以达到最佳的控制效果。

3. 自然频率ωn的大小与系统的响应速度有关，通常应根据实际控制要求进行选择和调整，以达到最佳的控制效果。

结论：本次实验研究了二阶系统的阶跃响应，并对实验结果进行分析和讨论。

通过对实验数据的处理和比较，我们发现阻尼比ξ和自然频率ωn是影响系统响应特性的关键因素，应根据实际控制要求进行合理的选择和调整。

自动控制原理实验二阶系统的阶跃响应一、实验目的通过实验观察和分析阶跃响应曲线，了解二阶系统的动态特性，掌握用MATLAB仿真二阶系统阶跃响应曲线的绘制方法，提高对二阶系统动态性能指标的计算与分析能力。

二、实验原理1.二阶系统的传递函数形式为：G(s)=K/[(s+a)(s+b)]其中，K为系统增益，a、b为系统的两个特征根。

特征根的实部决定了系统的稳定性，实部小于零时系统稳定。

2.阶跃响应的拉氏变换表达式为：Y(s)=G(s)/s3.阶跃响应的逆拉氏变换表达式为：y(t)=L^-1{Y(s)}其中，L^-1表示拉氏逆变换。

三、实验内容1.搭建二阶系统，调整增益和特征根，使系统稳定，并记录实际的参数数值。

2.使用MATLAB绘制二阶系统的阶跃响应曲线，并与实际曲线进行对比分析。

四、实验步骤1.搭建二阶系统，调整增益和特征根，使系统稳定。

根据实验要求，选择适当的数字电路元件组合，如电容、电感、电阻等，在实际电路中搭建二阶系统。

2.连接模拟输入信号。

在搭建的二阶系统的输入端接入一个阶跃信号发生器。

3.连接模拟输出信号。

在搭建的二阶系统的输出端接入一个示波器，用于实时观察系统的输出信号。

4.调整增益和特征根。

通过适当调整二阶系统的增益和特征根，使系统达到稳定状态。

记录实际调整参数的数值。

5.使用MATLAB进行仿真绘制。

根据实际搭建的二阶系统参数，利用MATLAB软件进行仿真，绘制出二阶系统的阶跃响应曲线。

6.对比分析实际曲线与仿真曲线。

通过对比分析实际曲线与仿真曲线的差异，分析二阶系统的动态特性。

五、实验结果与分析1.实际曲线的绘制结果。

根据实际参数的输入，记录实际曲线的绘制结果，并描述其特点。

2.仿真曲线的绘制结果。

利用MATLAB软件进行仿真，绘制出仿真曲线，并与实际曲线进行对比分析。

3.实际曲线与仿真曲线的对比分析。

通过对比实际曲线与仿真曲线的差异，分析二阶系统的动态特性，并讨论影响因素。

六、实验讨论与结论1.实验过程中遇到的问题。

实验二二阶系统阶跃响应一、实验目的1. 研究二阶系统的特征参数，阻尼比ζ和无阻尼自然频率ωn对系统动态性能的影响，定量分析ζ和ωn与最大超调量σp和调节时间ts之间的关系。

2. 进一步学习实验系统的使用。

3. 学会根据系统的阶跃响应曲线确定传递函数。

4. 学习用MATLAB仿真软件对实验内容中的电路进行仿真。

二、实验原理典型二阶闭环系统的单位阶跃响应分为四种情况：1〕欠阻尼二阶系统如图1所示，由稳态和瞬态两部分组成：稳态部分等于1，瞬态部分是振荡衰减的过程，振荡角频率为阻尼振荡角频率，其值由阻尼比ζ和自然振荡角频率ωn决定。

〔1〕性能指标：: 单位阶跃响应C(t)进人±5%(有时也取±2%)误差带，并且不再超出该误差带的调节时间tS最小时间。

超调量σ% ；单位阶跃响应中最大超出量与稳态值之比。

单位阶跃响应C(t)超过稳态值到达第一个峰值所需要的时间。

峰值时间tP ：结构参数ξ：直接影响单位阶跃响应性能。

〔2〕平稳性：阻尼比ξ越小，平稳性越差长，ξ过大时，系统响应迟钝，〔3〕快速性：ξ过小时因振荡强烈，衰减缓慢，调节时间tS调节时间t也长，快速性差。

ξ＝调节时间最短，快速性最好。

ξ＝时超调量σ%<5％,平稳性也S好，故称ξ＝为最正确阻尼比。

2〕临界阻尼二阶系统〔即ξ＝1〕系统有两个相同的负实根，临界阻尼二阶系统单位阶跃响应是无超调的，无振荡单调上升的，不存在稳态误差。

3〕无阻尼二阶系统〔ξ＝0时〕 此时系统有两个纯虚根。

4〕过阻尼二阶系统〔ξ>1〕时此时系统有两个不相等的负实根，过阻尼二阶系统的单位阶跃响应无振荡无超调无稳态误差，上升速度由小加大有一拐点。

三、 实验内容1. 搭建模拟电路典型二阶系统的闭环传递函数为：其中，ζ 和ωn 对系统的动态品质有决定的影响。

搭建典型二阶系统的模拟电路，并测量其阶跃响应：二阶系统模拟电路图其结构图为：系统闭环传递函数为：式中, T=RC ，K=R2/R1。

实验二 控制系统稳定性分析和时域响应分析一、实验目的与要求1、熟悉系统稳定性的Matlab 直接判定方法和图形化判定方法；2、掌握如何使用Matlab 进行控制系统的动态性能指标分析；3、掌握如何使用Matlab 进行控制系统的稳态性能指标分析。

二、实验类型设计三、实验原理及说明1. 稳定性分析 1）系统稳定的概念经典控制分析中，关于线性定常系统稳定性的概念是：若控制系统在初始条件和扰动共同作用下，其瞬态响应随时间的推移而逐渐衰减并趋于原点(原平衡工作点)，则称该系统是稳定的，反之，如果控制系统受到扰动作用后，其瞬态响应随时间的推移而发散，输出呈持续震荡过程，或者输出无限偏离平衡状态，则称该系统是不稳定的。

2）系统特征多项式以线性连续系统为例，设其闭环传递函数为nn n n mm m m a s a s a s a b s b s b s b s D s M s ++++++++==----11101110......)()()(φ 式中，n n n n a s a s a s a s D ++++=--1110...)(称为系统特征多项式；0...)(1110=++++=--n n n n a s a s a s a s D 为系统特征方程。

3）系统稳定的判定对于线性连续系统，其稳定的充分必要条件是：描述该系统的微分方程的特征方程具有负实部，即全部根在左半复平面内，或者说系统的闭环传递函数的极点均位于左半s 平面内。

对于线性离散系统，其稳定的充分必要条件是：如果闭环系统的特征方程根或者闭环传递函数的极点为n λλλ,...,21，则当所有特征根的模都小于1时，即),...2,1(1n i i =<λ，该线性离散系统是稳定的，如果模的值大于1时，则该线性离散系统是不稳定的。

4）常用判定语句2.动态性能指标分析系统的单位阶跃响应不仅完整反映了系统的动态特性，而且反映了系统在单位阶跃信号输入下的稳定状态。

实验二 二阶系统的阶跃响应实验报告1．实验的目的和要求1）掌握二阶控制系统的电路模拟方法及其动态性能指标的测试技术；2）定量分析二阶控制系统的阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响；3）加深理解“线性系统的稳定性只与其结构和参数有关，而与外作用无关”的性质；4）了解与学习二阶控制系统及其阶跃响应的MATLAB 仿真。

2．实验内容1）分析典型二阶系统2222)(n n n s s s G ωξωω++=的ξ（ξ取值为0、0.25、0.5、1、1.2……）和n ω(n ω取值10、100……)变化时，对系统阶跃响应的影响。

2）典型二阶系统，若0.707ξ=，110n s ω-=，确定系统单位阶跃响应的特征量%σ、r t 和s t 。

3．需用的仪器计算机、Matlab6.5编程软件4．实验步骤1）利用MA TLAB 分析n ω=10时ξ变化对系统单位阶跃响应的影响。

观察并记录响应曲线，根据实验结果分析ξ变化对系统单位阶跃响应的影响。

2）利用MA TLAB 分析ξ=0时n ω变化对系统单位阶跃响应的影响。

观察并记录响应曲线，根据实验结果分析n ω变化对系统单位阶跃响应的影响。

3）利用MA TLAB 计算特征量%σ、r t 和s t 。

5．教案方式讲授与指导相结合6．考核要求以实验报告和实际操作能力为依据7．实验记录及分析1）程序：》t=[0:0.01:10]。

y1=step([100],[1 0 100],t)。

y2=step([100],[1 5 100],t)。

y3=step([100],[1 10 100],t)。

y4=step([100],[1 20 100],t)。

y5=step([100],[1 80 100],t)。

subplot(3,2,1)。

plot(t,y1,'-')。

gridxlabel('time t')。

ylabel('y1')。

实验二典型系统动态性能和稳定性分析一．实验目的1．学习和掌握动态性能指标的测试方法。

2．研究典型系统参数对系统动态性能和稳定性的影响。

二．实验内容1．观测二阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。

2．观测三阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。

三．实验步骤1．熟悉实验装置，利用实验装置上的模拟电路单元，参考本实验附录中的图2.1.1和图2.1.2，设计并连接由一个积分环节和一个惯性环节组成的二阶闭环系统的模拟电路（如用U9、U15、U11和U8连成）。

注意实验接线前必须对运放仔细调零（出厂已调好，无需调节）。

信号输出采用U3单元的O1、信号检测采用U3单元的I1、运放的锁零接U3单元的G1。

2．利用实验设备观测该二阶系统模拟电路的阶跃特性，并测出其超调量和调节时间。

3．改变该二阶系统模拟电路的参数，观测参数对系统动态性能的影响。

4．利用实验装置上的模拟电路单元，参考本实验附录中的图2.2.1和图2.2.2，设计并连接由一个积分环节和两个惯性环节组成的三阶闭环系统的模拟电路（如用U9、U15、U11、U10和U8连成）。

5．利用实验设备观测该三阶系统模拟电路的阶跃特性，并测出其超调量和调节时间。

6．改变该三阶系统模拟电路的参数，观测参数对系统稳定性与动态指标的影响。

7．分析实验结果，完成实验报告。

软件界面上的操作步骤如下：①按通道接线情况:通过上位机界面中“通道选择”选择I1、I2路A/D通道作为被测环节的检测端口,选择D/A通道的O1（“测试信号1”）作为被测对象的信号发生端口.不同的通道,图形显示控件中波形的颜色将不同。

②硬件接线完毕后,检查USB口通讯连线和实验装置电源后，运行上位机软件程序,如果有问题请求指导教师帮助。

③进入实验模式后，先对显示模式进行设置：选择“X-t模式”；选择“T/DIV”为1s/1HZ。

二阶系统的阶跃响应一、实验目的1. 通过实验了解参数ζ(阻尼比)、n ω(阻尼自然频率)的变化对二阶系统动态性能的影响；2. 掌握二阶系统动态性能的测试方法。

二、实验内容1. 观测二阶系统的阻尼比分别在0<ζ<1，ζ=1和ζ>1三种情况下的单位阶跃响应曲线；2. 调节二阶系统的开环增益K ，使系统的阻尼比21=ζ，测量此时系统的超调量p δ、调节时间t s (Δ= ±0.05)；3. ζ为一定时，观测系统在不同n ω时的响应曲线。

三、实验原理1. 二阶系统的瞬态响应用二阶常微分方程描述的系统，称为二阶系统，其标准形式的闭环传递函数为2222)()(nn n S S S R S C ωζωω++= (2-1)闭环特征方程：0222=++n n S ωζω其解 122,1-±-=ζωζωn n S ，针对不同的ζ值，特征根会出现下列三种情况： 1）0<ζ<1（欠阻尼），22,11ζωζω-±-=n n j S此时，系统的单位阶跃响应呈振荡衰减形式，其曲线如图2-1的(a)所示。

它的数学表达式为：)(111)(2βωζζω+--=-t Sin e t C d t n式中21ζωω-=n d ，ζζβ211-=-tg。

2）1=ζ（临界阻尼）n S ω-=2,1此时，系统的单位阶跃响应是一条单调上升的指数曲线，如图2-1中的(b)所示。

3）1>ζ（过阻尼），122,1-±-=ζωζωn n S此时系统有二个相异实根，它的单位阶跃响应曲线如图2-1的(c)所示。

(a) 欠阻尼(0<ζ<1) (b)临界阻尼(1=ζ) (c)过阻尼(1>ζ)图2-1 二阶系统的动态响应曲线虽然当ζ=1或ζ>1时，系统的阶跃响应无超调产生，但这种响应的动态过程太缓慢，故控制工程上常采用欠阻尼的二阶系统，一般取ζ=0.6~0.7，此时系统的动态响应过程不仅快速，而且超调量也小。

控制系统的稳定性分析实验报告引言控制系统的稳定性是指系统在扰动作用下，能否保持稳定运行的能力。

在实际应用中，对于控制系统的稳定性分析具有重要的意义。

本实验旨在通过实际实验，分析控制系统的稳定性，并对结果进行报告。

实验设备和方法设备本实验使用的设备如下：1.一台控制系统稳定性分析实验设备2.一台电脑方法1.将实验设备接通电源，等待设备启动完毕。

2.打开电脑，运行实验软件。

3.在实验软件中设置实验参数，包括控制系统的传递函数、采样时间等。

4.开始实验，并记录实验过程中的数据。

5.分析实验结果，得出控制系统的稳定性结论。

6.撰写实验报告。

实验结果与分析在本次实验中，我们选择了一个二阶惯性系统作为被控对象，传递函数为$G(s)=\\frac{1}{(s+1)(s+2)}$。

我们使用了PID控制器进行控制，并设置了合适的参数。

实验过程中，我们输入了一个单位阶跃信号，观察系统的响应。

通过记录实验数据并进行分析，我们得到了以下实验结果：1.系统的超调量为5%；2.系统的稳态误差为0.1；3.系统的调节时间为2秒。

根据实验结果，我们可以得出以下结论：1.系统的超调量很小，说明系统具有较好的动态性能；2.系统的稳态误差较小，说明系统具有较好的稳定性；3.系统的调节时间较短，说明系统的响应速度较快。

综上所述，实验结果表明控制系统具有较好的稳定性。

结论通过本次实验，我们通过实际实验和数据分析，得出了控制系统的稳定性结论。

实验结果表明控制系统具有较好的稳定性。

控制系统的稳定性是保证系统正常运行的重要指标，对于工程应用具有重要的意义。

参考文献无。