4.2 离散无记忆信源R(D)的计算-- 4.5 保真度准则下的信源编码定理解析
- 格式:ppt
- 大小:331.00 KB
- 文档页数:40




信息论与编码研学笔记一、信息论与编码研学的详细过程1.阅读了教材或参考资料上的哪些内容?第一章绪论:§1.1 信息的一般概念信息存在于自然界,也存在于人类社会,其本质是运动和变化。
可以说哪里有事物的运动和变化,哪里就会产生信息。
信息必须依附于一定的物质形式存在,这种运载信息的物质,称为信息载体。
人类交换信息的形式丰富多彩,使用的信息载体非常广泛。
概括起来,有语言、文字和电磁波。
§1.2 信息的分类在众多的分类原则和方法中,最重要的就是按照信息性质的分类。
按照性质的不同可以把信息划分成语法信息、语义信息和语用信息三个基本类型。
其中最基本也是最抽象的类型是语法信息。
也是迄今为止在理论上研究得最多的类型。
§1.3 信息论的起源、发展及研究内容在人类历史的长河中,信息传输和传播手段经历了五次重大变革:语言的产生;文字的产生;印刷术的发明;电报、电话的发明;计算机与通信技术相结合,促进了网络通信的发展。
第2章:信源熵§2.1 单符号离散信源单符号离散信源的数学模型、自信息和信源熵、信源熵的基本性质和定理、加权熵的概念和基本性质、平均互信息、各种熵之间的关系§2.2 多符号离散信源序列信息的熵、离散平稳信源的数学模型、平稳信源的熵和极限熵、马尔可夫信源、信源冗余度§2.3 连续信源连续信源的熵、几种特殊连续信源的熵、连续信源熵的性质及最大连续熵定理、熵功率§2.4 离散信源无失真编码定理定长编码定理、变长编码定理第3章:信道容量§3.1 信道容量的数学模型和分类§3.2 单符号离散信源信道容量的定义、几种特殊离散信道的容量、离散信道容量的一般计算方法§3.3 多符号离散信源多符号离散信道的数学模型、离散无记忆信道的N次扩展信道和独立并联信道的信道容量§3.4 多用户信道多址接入信道、广播信道、相关信源的多用户信道§3.5 信道编码定理第4章:信息率失真函数§4.1 信息率失真函数失真函数和平均失真度、率失真函数定义、率失真函数性质§4.2 离散信源的信息率失真函数离散信源信息率失真函数的参量表达式、二元信源的率失真函数连续信息的率失真函数、连续信源失真函数的参量表达式、高斯信源的率失真函数、信息价值§4.4 保真度准则下的信源编码定理第5章:信源编码§5.1 离散信源编码香农编码、费诺编码、赫夫曼编码、游程编码、冗余位编码§5.2 连续信源编码最佳标量量化、矢量量化§5.3 相关信源编码预测编码、差值编码§5.4 变差值编码子带编码、小波变换第6章:信道编码§6.1 信道编码的概念信道编码的作用和分类、编码信道、检错和纠错原理、检错和纠错方式和能力§6.2 线形分组码线性分组码的描述、线性分组码的译码、码例与码的重构§6.3 循环码循环码的多项式描述、循环码的生成矩阵、系统循环码、多项式运算电路、循环码的编码电路、循环码的伴随多项式与检测、BCH 码与RS 码 §6.4 卷积码卷积码的矩阵描述、卷积码的多项式描述、卷积码的状态转移图与格描述、维特比(Viterbi )译码算法第7章:密码体制的安全性测度§7.1 密码基本知识§7.2 古典密码体制§7.3 现代密码体制§7.4 密码体制的安全性测度2.证明了教材或参考资料上哪些没有证明的定理?1)最大离散熵定理:离散无记忆信源输出M 个不同的信息符号,当且仅当各个符号出现概率相等时(即pi=1/M ),熵最大。



《信息论与编码》教学大纲课程编码:1041812课程性质:专业课程适用专业:电子信息工程学分:2学分学时:36学时开设学期:第5学期一、教学目的本课程的教学目的是使学生掌握信息处理的理论基础和各种编码原理、手段与方法。
培养学生能够适应数字通信、信息处理、信息安全、计算机信息管理等编码工作的要求。
使学生掌握信息理论的基本概念和信息分析方法及主要结论,为今后从事信息领域的科研及工程工作的进一步研究打下坚实的理论基础。
二、教学重点与难点1.重点:信息以及失真的测度、信道及信道容量、无失真信源编码方法以及有噪信道编码方法。
2.难点: 典型序列以及由此推导出的香农三大编码定理及其逆定理。
三、教学方法建议讲授法:教师讲授信息论与编码的基本知识和研究现状。
讨论法:师生共同讨论信息论与编码中研究的问题。
探究法:师生共同探究信息论与编码中前沿问题。
四、教学内容第一章信息理论基础(4学时)教学要求:了解信息论研究对象、目的、发展简史与现状;了解通信系统的模型以及通信系统各部分的主要组成以及作用。
1.信息论的形成和发展2.通信系统的模型3.信息论研究的内容第二章离散信源及其测度(8学时)教学要求:了解信源的相关性和剩余度的概念,消息、信息、信号的概念,信息,信号,消息,数据的关系及其联系。
掌握信源的数学模型、离散无记忆信源、离散平稳信源和马尔可夫信源基本理论。
1.信源的数学模型及分类2.信息熵及其基本性质3.离散平稳信源4.马尔可夫信源5.信息剩余度第三章离散信道及其信道容量(8学时)教学要求:了解一般信道容量的计算方法。
掌握信道的数学模型,离散无记忆信道以及一些特殊信道容量的计算方法。
1.信道数学模型及分类2.平均互信息及特点3.信道容量及一般计算方法4.离散无记忆扩展信道及其容量第四章无失真信源编码(8学时)教学要求:了解其它一些无失真信源编码方法;理解渐近等分割性及ε典型序列,算术编码方法及具体实现方案;掌握编码的定义、码的分类、定长编码定理、变长编码定理、最佳编码方法、香农编码方法、费诺编码方法、哈夫曼编码方法。


第三章 信源编码——离散信源无失真编码本章分析问题:在信宿要求无失真接收时,或所有信源信息无损的条件下,离散信源输出的表示——即信源编码问题。
内容:信源分类,信息速率的计算,编码定理,有效编码方法等。
一、信源及其分类 1. 离散信源和连续信源离散信源表示:…U-2U-1U0U1U2…其中UL随机变量,取值范围:A={a1,a2,…ak} 2.无记忆源和有记忆源无记忆源:各UL彼此统计独立简单信源:各UL彼此统计独立且服从同一概率分布 P(UL=ak)=Pk,k=1,2,…,K∑=Kk 1Pk=1有记忆源:各UL取值相关。
UL=(U1,U2,…,UL)∈UL,其概率分布由L维随机矢量表示,P(UL=a)=P(U1=ak1,…,UL=akL) 3.平稳信源:概率分布与起始下标无关P(U1=ak1,…,UL=akL)=P(Ut+1=ak1,…,UL=akL)4.各态历经源:信源输出的随机序列具有各态历经性。
5.有限记忆源:用条件概率P(UL,UL-1,UL-2,UL-m)表述。
m为记忆阶数。
6.马尔可夫源:有限记忆源可用有限状态马尔可夫链描述,当m=1时为简单马尔可夫链。
7.时间离散的连续源:各随机变量UL取值连续。
8.随机波形源:时间和取值上均连续的信源;由随机过程u(t)描述,时间或频率上有限的随机过程可展开成分量取值连续的随机矢量表示,即时间上离散,取值连续的信源。
9.混合信源二、离散无记忆源的等长编码离散无记忆源:DMSL长信源输出序列:UL=(U1,U2,…,UL),Ul取值{a1,a2,…ak},共KL种不同序列。
对每个输出序列用D元码进行等长编码,码长为N,则可选码共有DN个。
1.单义可译码或唯一可译码:条件:DN≥KL=M,即N≥LlogK/logDN/L:每个信源符号所需的平均码元数;N/L→3.322;2.信息无损编码要求:设每个信源符号的信息量为H(U),则L长信源序列的最大熵值为LH(U),编码时由于D个码元独立等概时携带信息量最大,使码长最短。

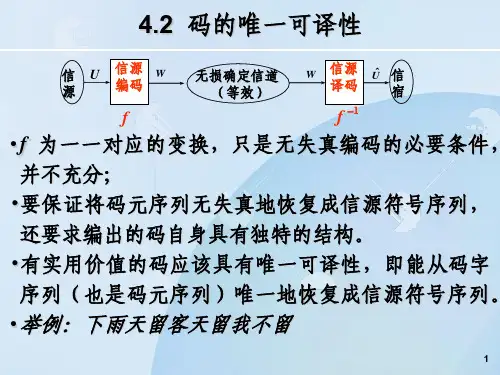
第4章离散无记忆信源无失真编码主要内容1、基本概念2、码的唯一可译性3、定长编码定理和定长编码方法4、变长编码定理5 变长编码方法6 几种实用的无失真信源编码1、基本概念信源发出的消息序列通常不能直接送给信道传输,需要经过信源编码和信道编码。
信道编码的目的是降低差错率,提高传送的可靠性。
信源编码的目的是为了降低冗余度,提高通信的有效性。
编码是一种映射,是将输入符号映射成码字。
无失真编码,映射一一对应,可逆。
编码器模型:码长:码字所含码元的个数定长编码:所有码字均有相同的码长,对应的码叫做定长码(FLC ,Fixed Length code);否则为变长编码。
编码器12{,,,}q u u u 12{,,,}r x x x WU12{,,,}q w w w X信源平均码长:码中所有码字码长的统计平均,即码元/符号编码效率:编码后的实际信息率与编码后的最大信息率之比冗余度:l l l2、码的唯一可译性(1)基本概念奇异码:一组码中含相同码字。
非奇异码:所有的码字都不相同。
唯一可译性:码字组成的任意有限长码字序列都能恢复成唯一的信源序列。
续长码:有些码字是在另一些码字后面添加码元得来的。
及时码:码字的最后一个码元出现时,译码器能立即判断一个码字已经结束,可以立即译码。
非续长码:任一码字都不是其它码字的延长。
唯一可译码定长非奇异码非续长码非奇异码5种不同的码35124121142183184()00001000100001001101001110011111110111111i P u W W W W W U u u u u(2)码树和Kraft不等式从树根开始,生长r个树枝,在节点处再各自生长r个树枝。
节点:树枝与树枝的交点。
l阶节点:经过l根树枝到达的节点。
整树:节点长出的树枝数等于r定理:对于任一r进制非续长码,各码字的码长必须满足Kraft不等式:反过来,若上式成立,就一定能构造一个r 进制非续长码。
1、 在认识论层次上研究信息的时候,必须同时考虑到 形式、含义和效用 三个方面的因素。
2、 1948年,美国数学家 香农 发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
3、 按照信息的性质,可以把信息分成 语法信息、语义信息和语用信息 。
4、 按照信息的地位,可以把信息分成 客观信息和主观信息 。
5、 人们研究信息论的目的是为了 高效、可靠、安全 地交换和利用各种各样的信息。
6、 信息的 可度量性 是建立信息论的基础。
7、 统计度量 是信息度量最常用的方法。
8、 熵 是香农信息论最基本最重要的概念。
9、 事物的不确定度是用时间统计发生 概率的对数 来描述的。
10、单符号离散信源一般用随机变量描述,而多符号离散信源一般用 随机矢量 描述。
11、一个随机事件发生某一结果后所带来的信息量称为自信息量,定义为 其发生概率对数的负值 。
12、自信息量的单位一般有 比特、奈特和哈特 。
13、必然事件的自信息是 0 。
14、不可能事件的自信息量是 ∞ 。
15、两个相互独立的随机变量的联合自信息量等于 两个自信息量之和 。
16、数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量 趋于变小 。
17、离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍 。
18、离散平稳有记忆信源的极限熵,。
19、对于n 元m 阶马尔可夫信源,其状态空间共有 n m 个不同的状态。
20、一维连续随即变量X 在[a ,b]区间内均匀分布时,其信源熵为 log 2(b-a ) 。
21、平均功率为P 的高斯分布的连续信源,其信源熵,H c (X )=。
22、对于限峰值功率的N 维连续信源,当概率密度 均匀分布 时连续信源熵具有最大值。
23、对于限平均功率的一维连续信源,当概率密度 高斯分布 时,信源熵有最大值。
24、对于均值为0,平均功率受限的连续信源,信源的冗余度决定于平均功率的限定值P 和信源的熵功率 之比 。