第7讲——离散无记忆信源等长编码

第三章 离散信源无失真编码3.2离散无记忆信源，熵为H[x]，对信源的L 长序列进行等长编码，码字是长为n 的D 进制符号串，问：（1）满足什么条件，可实现无失真编码。

（2）L 增大，编码效率 也会增大吗？ 解：（1）当log ()n D LH X ≥时，可实现无失真编码；（2）等长编码时，从总的趋势来说，增加L 可提高编码效率，且当L →∞时，1η→。

但不一定L 的每次增加都一定会使编码效率提高。

3.3变长编码定理指明，对信源进行变长编码，总可以找到一种惟一可译码，使码长n 满足D X H log )(≤n <D X H log )(+L 1,试问在n >D X H log )(+L1时，能否也找到惟一可译码？ 解：在n >D X H log )(+L1时，不能找到惟一可译码。

证明：假设在n >D X H log )(+L1时，能否也找到惟一可译码，则由变长编码定理当n 满足D X H log )(≤n <D X H log )(+L 1，总可以找到一种惟一可译码知：在n ≥DX H log )( ① 时，总可以找到一种惟一可译码。

由①式有：Ln ≥L X H )(logD ② 对于离散无记忆信源，有H(x)=LX H )( 代入式②得：n L≥ D x H log )(即在nL≥Dx H log )(时，总可以找到一种惟一可译码；而由定理给定熵H （X ）及有D 个元素的码符号集，构成惟一可译码，其平均码长满足D X H log )(≤n L <DX H log )(+1 两者矛盾，故假设不存在。

所以，在n >D X H log )(+L1时，不能找到惟一可译码。

3.7对一信源提供6种不同的编码方案：码1~码6，如表3-10所示信源消息 消息概率 码1 码2 码3 码4 码5 码6 u1 1/4 0 001 1 1 00 000 u2 1/4 10 010 10 01 01 001 U3 1/8 00 011 100 001 100 011 u4 1/8 11 100 1000 0001 101 100 u5 1/8 01 101 10000 00001 110 101 u6 1/16 001 110 100000 000001 1110 1110 u71/161111111000000000000111111111（1） 这些码中哪些是惟一可译码？ （2） 这些码中哪些是即时码？（3） 对所有唯一可译码求出其平均码长。

3.1离散无记忆信源等长编码3.1离散无记忆信源等长编码3.1离散无记忆信源等长编码几乎无失真等长编码选择L 足够长，使N log D ≥L [H (U ) +εL ]εL 为与L 有关的正数，且当L →∞时有εL →0, 才其中，能不损失信息。

然而这样的编码不总能保证单义可译，但非单义可译所引起的错误可渐近为任意小。

反之，若N log D3.2 离散无记忆（简单）信源的等长编码编码速率R =N log D /L R =N log D /L ≥log K关于编码速率的说明：表示一个长度为N 的D 元码字给一个长度为L 的消息的每个符号所提供的信息量。

3.2 离散无记忆（简单）信源的等长编码一个消息序列U L 每符号含有信息量算术平均为：I L =I (u L ) /L =∑I (u l ) /Ll信源的熵为H(U)E (I (u l ))=∑p (a k ) I (a k ) =H (U )k设I (u l ) 的方差为σI 2σ=D (I (u l ))=∑p (a k ) (I (a k ) ?H (U ))2Ik23.2 离散无记忆（简单）信源的等长编码例信源发出的消息序列长度L=8。

a 2??a 1u l ~??1/43/4?I (a 1)I (a 2)?I (u l )~??3/4??1/42H (U )=0.81bitσ=D (I (u l ))=∑p (a k ) (I (a k ) ?H (U ))=0.4712Ik长为8的序列是(a1+a2) 8的展开式的所有项，共28个。

消息序列的概率是(p1+p2) 8的二项展开式中的各项。

I 8(a 18)=I (a 18)/8=I (a 1)5I 8(a 13a 2)=(3I (a 1)+5I (a 2))/83.2 离散无记忆（简单）信源的等长编码3.2.2 信源划分定理典型序列集的定义令H(U)是集{U , p (a k ) }的熵，ε>0，T U (L , ε) ={u L :H (U ) ?ε≤I L ≤H (U ) +ε}(IL=I (u L )/L , u L ∈UL)定义为给定信源U 输出长为L 的典型序列集T U (L , ε) 的补集它称作弱ε典型序列集；相应地，为非典型序列集。

第三章 信源编码——离散信源无失真编码本章分析问题：在信宿要求无失真接收时，或所有信源信息无损的条件下，离散信源输出的表示——即信源编码问题。

内容：信源分类，信息速率的计算，编码定理，有效编码方法等。

一、信源及其分类 1． 离散信源和连续信源离散信源表示：…Ｕ－２Ｕ－１Ｕ０Ｕ１Ｕ２…其中ＵＬ随机变量，取值范围：Ａ＝｛ａ１，ａ２，…ａｋ｝ ２．无记忆源和有记忆源无记忆源：各ＵＬ彼此统计独立简单信源：各ＵＬ彼此统计独立且服从同一概率分布 Ｐ（ＵＬ＝ａｋ）＝Ｐｋ，ｋ＝１，２，…，Ｋ∑=Kk 1Ｐｋ＝１有记忆源：各ＵＬ取值相关。

ＵＬ＝（Ｕ１，Ｕ２，…，ＵＬ）∈ＵＬ，其概率分布由Ｌ维随机矢量表示，Ｐ（ＵＬ＝ａ）＝Ｐ（Ｕ１＝ａｋ１，…，ＵＬ＝ａｋＬ） ３．平稳信源：概率分布与起始下标无关Ｐ（Ｕ１＝ａｋ１，…，ＵＬ＝ａｋＬ）＝Ｐ（Ｕｔ＋１＝ａｋ１，…，ＵＬ＝ａｋＬ）４．各态历经源：信源输出的随机序列具有各态历经性。

５．有限记忆源：用条件概率Ｐ（ＵＬ，ＵＬ－１，ＵＬ－２，ＵＬ－ｍ）表述。

ｍ为记忆阶数。

６．马尔可夫源：有限记忆源可用有限状态马尔可夫链描述，当ｍ＝１时为简单马尔可夫链。

７．时间离散的连续源：各随机变量ＵＬ取值连续。

８．随机波形源：时间和取值上均连续的信源；由随机过程ｕ（ｔ）描述，时间或频率上有限的随机过程可展开成分量取值连续的随机矢量表示，即时间上离散，取值连续的信源。

９．混合信源二、离散无记忆源的等长编码离散无记忆源：ＤＭＳＬ长信源输出序列：ＵＬ＝（Ｕ１，Ｕ２，…，ＵＬ），Ｕｌ取值｛ａ１，ａ２，…ａｋ｝，共ＫＬ种不同序列。

对每个输出序列用Ｄ元码进行等长编码，码长为Ｎ，则可选码共有ＤＮ个。

１．单义可译码或唯一可译码：条件：ＤＮ≥ＫＬ＝Ｍ，即Ｎ≥ＬｌｏｇＫ／ｌｏｇＤＮ／Ｌ：每个信源符号所需的平均码元数；Ｎ／Ｌ→３．３２２；２．信息无损编码要求：设每个信源符号的信息量为Ｈ（Ｕ），则Ｌ长信源序列的最大熵值为ＬＨ（Ｕ），编码时由于Ｄ个码元独立等概时携带信息量最大，使码长最短。

第七章 信源编码7-1已知某地天气预报状态分为六种：晴天、多云、阴天、小雨、中雨、大雨。

① 若六种状态等概出现，求每种消息的平均信息量及等长二进制编码的码长N 。

② 若六种状态出现的概率为：晴天—0.6；多云—0.22；阴天—0.1；小雨—0.06；中雨—0.013；大雨—0.007。

试计算消息的平均信息量，若按Huffman 码进行最佳编码，试求各状态编码及平均码长N 。

解: ①每种状态出现的概率为6,...,1,61==i P i因此消息的平均信息量为∑=-===6122/58.26log 1log i ii bit P P I 消息 等长二进制编码的码长N ＝[][]316log 1log 22=+=+L 。

②各种状态出现的概率如题所给，则消息的平均信息量为6212222221log 0.6log 0.60.22log 0.220.1log 0.10.06log 0.060.013log 0.0130.007log 0.0071.63/i i iI P P bit -== = ------ ≈ ∑消息Huffman 编码树如下图所示：由此可以得到各状态编码为：晴—0，多云—10，阴天—110，小雨—1110，中雨—11110， 大雨—11111。

平均码长为：6110.620.2230.140.0650.01350.0071.68i ii N n P == =⨯+⨯+⨯+⨯+⨯+⨯ =∑—7-2某一离散无记忆信源（DMS ）由8个字母(1,2,,8)i X i =⋅⋅⋅组成，设每个字母出现的概率分别为：0.25，0.20，0.15，0.12，0.10，0.08，0.05，0.05。

试求： ① Huffman 编码时产生的8个不等长码字； ② 平均二进制编码长度N ； ③ 信源的熵，并与N 比较。

解：①采用冒泡法画出Huffman 编码树如下图所示可以得到按概率从大到小8个不等长码字依次为：0100,0101,1110,1111,011,100,00,1087654321========X X X X X X X X②平均二进制编码长度为8120.2520.2030.1530.1240.140.0840.0540.052.83i ii N n P == =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯ =∑ ③信源的熵∑=≈-=81279.2log)(i i i P P x H 。

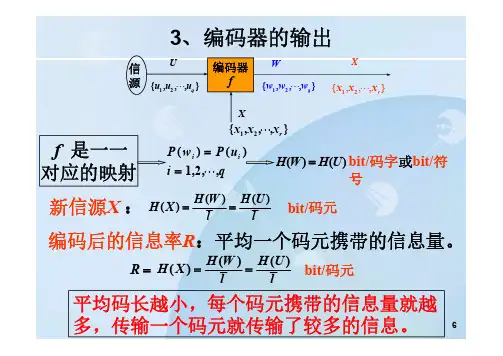
3、编码器的输出f 是一一对应的映射i i P w P u i q()()1,2,, H W H U ()()bit/码字或bit/符号H W H U H X l l()()()bit/码元新信源X ：编码后的信息率R ：平均一个码元携带的信息量。

H W H U H X l l()()()bit/码元平均码长越小，每个码元携带的信息量就越多，传输一个码元就传输了较多的信息。

R X{,,,}12r x x x 编码器f12{,,,}q u u u 12{,,,}r x x x WU12{,,,}q w w w X信源4、编码效率为了衡量编码效果，定义编码效率：编码后的实际信息率与编码后的最大信息率之比。

max max ()()()()log log c R H X H U l H U R H X r l r注：编码效率实际上也是新信源X 的信息含量效率或熵的相对率。

新信源的冗余度也是码的冗余度：1c c X{,,,}12rx x x 编码器f12{,,,}q u u u 12{,,,}r x x x WU12{,,,}q w w w X信源5种不同的码i P u W W W W W U u u u u 351241234()1200001001401000010011810100111001118111110111111W 1: 定长码。

W 3: 变长码。

奇异码。

定长非奇异码肯定是UDC u u u u u u u u u u u u u12434321121211,00,10,010110,01,00,11,00,1,00,1W 2: 定长码。

W 4: 变长码。

W 5: 变长码。

非奇异码。

非奇异码。

非奇异码。

非奇异码。

续长码。

非续长码。

续长码。

及时码。

非及时码。

奇异码肯定不是UDC不是UDC非续长码肯定是UDC 是UDC非及时码。

非续长码。

W 3：1001001唯一可译码定长非奇异码非续长码非奇异码码奇异码非奇异码非唯一可译码唯一可译码定长非奇异码变长非续长码（部分）变长续长码4.3 定长编码定理和定长编码方法1、对信源输出的符号序列进行编码DMS编码器f12{,,,}q u u u 12{,,,}r x x x WU 12{,,,}q w w w XX12{,,,}r x x x DMS编码器f 12{,,,}N q 12{,,,}r x x x WNU 12{,,,}Nq w w w XX12{,,,}r x x x 对信源U 的单个符号进行编码对信源U 的N 长符号串进行编码对扩展信源U N 的单个符号进行编码12i i i iNu u u 1212,,,{,,,}i i iN q u u u u u u2、定长编码定理r 进制定长编码,码长为l N , 可用的码字数目：Nl r Nl Nrq唯一可译max max ()log ()log log N r H U l q H U N r r信息传输率编码效率()()/N H U R H X l Nmax ()()()log c NH X H U l H X r Nbit/码元DMS编码器f 12{,,,}Nq 12{,,,}r x x x W NU 12{,,,}N q w w w XX12{,,,}r x x x定长无失真编码定理：用r 元符号表对离散无记忆信源U 的N 长符号序列进行定长编码，N 长符号序列对应的码长为l N ，若对于任意小的正数ε，有不等式:就几乎能做到无失真编码，且随着序列长度N 的增大，译码差错率趋于0。