土的侧压力系数和泊松比

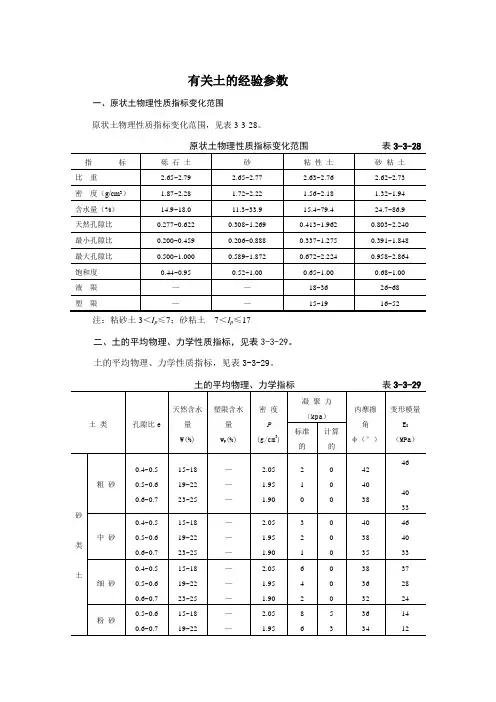
有关土的经验参数一、原状土物理性质指标变化范围原状土物理性质指标变化范围，见表3-3-28。

注：粘砂土3＜I p≤7；砂粘土7＜I p≤17二、土的平均物理、力学性质指标，见表3-3-29。

土的平均物理、力学性质指标，见表3-3-29。

注：①平均比重采取：砂——2.66；粘砂土——2.70；砂粘土——2.71；粘土——2.74；②粗砂和中砂的E 0值适用于不均匀系数C u = = 3者，当C u ＞5时应按表中所列值减少 。

C u为中间值时E 0 值按内插法确定；③对于地基稳定计算，采用人摩擦角φ的计算值低于标准值2°。

1060d d 32三、土的压缩模量一般范围值土的压缩模量一般范围值，见表3-3-3-。

注：砂粘土7＜I p≤7；粘土I p＞17四、粘性土剪强度参考值粘性土抗剪强度参考值，见表3-3-31。

注：粘砂土3＜I p≤7；砂粘土7＜I p≤7；粘土I p＞17五、土的侧压力系数（ξ）和泊松比（u）参考值注：粘土I p＞17；粉质粘土10＜I p≤17；I p≤10五、变形模量于压缩模量的关系变形模量E0是指土体在无侧限条件下应力与应变之比，其中的应变包含弹性应变和塑性应变两部分。

因此，变形模量较弹性模量E小，通常在土与基础的共同作用分析中用变形模量E。

变形模量一般是通过现场载荷试验确定，一些地方通过静力触探、标贯试验与变形模量建立了经验公式。

压缩模量Es是在侧限条件下应力与应变的比值，是通过室内试验获取的参数。

两者的关系：对于软土E0近似等于Es；较硬土层，E0=βEs，β=2～8，土愈坚硬，倍数愈大。

变形模量的定义在表达式上和弹性模量是一样的E=ζ/ε，对于变形模量ε是指应变，包括弹性应变εe和塑性应变εp，对于弹性模量而言，ε就是指εe(计算变形模量时，应变ε包括了弹性应变和塑性应变)。

岩土的弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

弹性模量>压缩模量>变形模量。

弹性模量也叫杨氏模量（岩土体在弹性限度内应力与应变的比值）压缩模量是有侧限的，杨氏模量是无侧限的。

同样的土体，同样的荷载，有侧限的土体应变小，所以压缩模量更大才对。

这只是弹性理论上的关系，对土体这种自然物不一定适用。

土体计算中所用的称为“弹性模量”不一定是在弹性限度内。

E——弹性模量；Es——压缩模量；Eo——变形模量。

弹性模量＝应力/弹性应变，它主要用于计算瞬时沉降。

压缩模量和变形模量均＝应力/总应变。

压缩模量是通过现场取原状土进行实验室有侧限压缩实验得出的，而变形模量则是通过现场的原位载荷试验得出的，它是无侧限的。

弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

地堪报告中，一般给出的是土的压缩模量Es与变形模量Eo，而一般不会给出弹性模量E。

数值模拟中一般用Eo，E（50），达到峰值应力（应变）50％时的割线模量。

Es（勘查报告中提供），有侧限，E＝2.0～5.0Es（看别人这么弄的）。

具体请查阅资料。

Eo应该是变形模量,E是弹性模量,Es是压缩模量,弹性模量与压缩模量应该有上百倍的关系吧,不应该只有五倍,一般e =3~5 es ;根据结果调整参数；问题是地质报告上只会提供压缩模量；工程上，土的弹性模量就是指变形模量，因为土发生弹性变形的时间非常短，变形模量与压缩模量是一个量级，但是由于土体的泊松比小于0.5，所以土的变形模量（弹性模量）总是小于压缩模量的。

在钱家欢主编的《土力学》P86中有公式：E = Es(1-2v^2/(1-v)) Es为变形模量，E为变形模量（弹性模量）。

事实上这些模量各有适用范围，本质上是为了在实验室或者现场模拟为再现实际工况而获取的值。

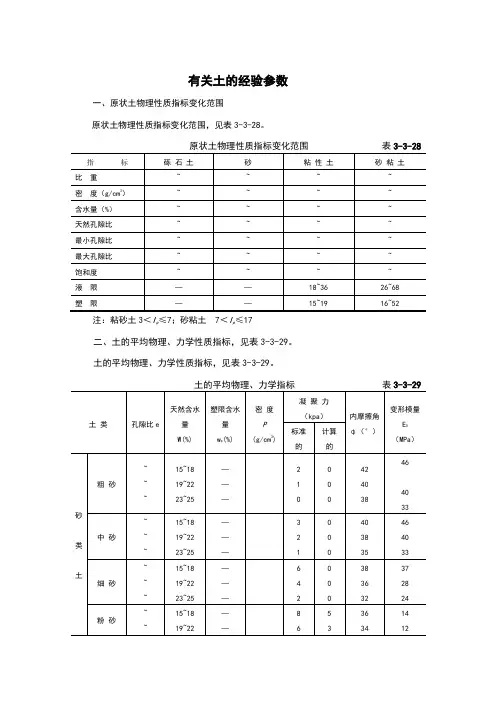
有关土的经验参数一、原状土物理性质指标变化范围
原状土物理性质指标变化范围，见表3-3-28。

注：粘砂土3＜I p≤7；砂粘土 7＜I p≤17
二、土的平均物理、力学性质指标，见表3-3-29。

土的平均物理、力学性质指标，见表3-3-29。

注：①平均比重采取：砂——；粘砂土——；砂粘土——；粘土——；
②粗砂和中砂的E 0值适用于不均匀系数C u = = 3者，当C u ＞5时应按表中所列值减少 。

C u
为中间值时E 0 值按内插法确定；
③对于地基稳定计算，采用人摩擦角φ的计算值低于标准值2°。

10
60d d 32
三、土的压缩模量一般范围值
土的压缩模量一般范围值，见表3-3-3-。

注：砂粘土7＜I p≤7；粘土I p＞17
四、粘性土剪强度参考值
粘性土抗剪强度参考值，见表3-3-31。

注：粘砂土3＜I p≤7；砂粘土7＜I p≤7；粘土I p＞17
五、土的侧压力系数（ξ）和泊松比（u）参考值
注：粘土I p＞17；粉质粘土10＜I p≤17；I p≤10
五、变形模量于压缩模量的关系
变形模量E0是指土体在无侧限条件下应力与应变之比，其中的应变包含弹性应变和塑性应变两部分。

因此，变形模量较弹性模量E小，通常在土与基础的共同作用分析中用变形模量E。

变形模量一般是通过现场载荷试验确定，一些地方通过静力触探、标贯试验与变形模量建立了经验公式。

压缩模量Es是在侧限条件下应力与应变的比值，是通过室内试验获取的参数。

两者的关系：对于软土E0近似等于Es；较硬土层，E0=βEs，β=2～8，土愈坚硬，倍数愈大。

c20混凝土侧压力系数混凝土的侧压力系数是指混凝土在受压时抵抗侧向膨胀的能力。

混凝土结构中的侧压力系数是无量纲的，通常用k表示，是一个关于材料本身和加载方式的固有性质。

一、混凝土侧压力系数的含义和计算方法：混凝土的侧压力系数表示了混凝土的抵抗侧向膨胀的能力，与混凝土的体积膨胀系数和材料的弹性性质有关。

混凝土结构受到压力时，由于体积受限，会产生侧向膨胀的效应。

侧面受到的约束力会对混凝土的体积膨胀产生一定的抑制作用，从而导致混凝土内部产生应力。

侧压力系数可以反映受到约束后的体积膨胀的抑制程度。

混凝土侧压力系数的计算可以根据国际标准、国家标准或文献中的公式进行。

一般来说，混凝土的侧压力系数可以通过以下公式进行计算：k = E × ν × k0其中，k表示混凝土的侧压力系数，E表示混凝土的弹性模量，ν表示混凝土的泊松比，k0表示混凝土的体积膨胀系数。

二、影响混凝土侧压力系数的因素：1. 混凝土的弹性性质：混凝土的弹性模量和泊松比是影响侧压力系数的主要因素。

弹性模量表示材料的刚度，泊松比表示材料在拉伸时沿垂直方向的收缩程度。

弹性模量越大，泊松比越小，混凝土的侧压力系数就越大。

2. 混凝土的体积膨胀系数：混凝土的体积膨胀系数是材料在受到约束时体积变化的比例。

体积膨胀系数越小，混凝土的侧压力系数就越大。

3. 加载方式和约束条件：混凝土的侧压力系数会受到加载方式和约束条件的影响。

在不同的加载方式下，混凝土的体积膨胀和侧压力系数会有所不同。

4. 混凝土的配合比和材料特性：混凝土的配合比和材料特性会影响混凝土的力学性能，进而影响侧压力系数。

三、混凝土侧压力系数的应用：混凝土侧压力系数在工程设计、结构分析和安全评估中起着重要的作用。

1. 工程设计：混凝土的侧压力系数在桥梁、坝体、隧道结构等工程设计中的压力计算和构件设计中起着重要作用。

2. 结构分析：混凝土的侧压力系数是进行结构强度和稳定性分析的重要参数，能够提供结构在受压时的有效计算结果。

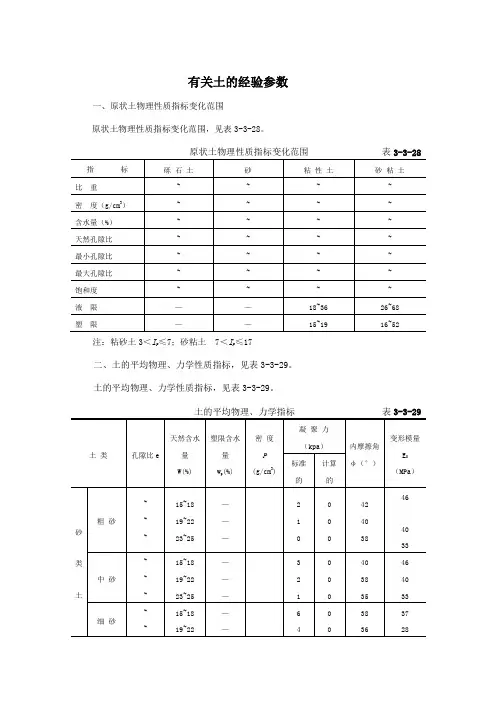
有关土的经验参数一、原状土物理性质指标变化范围原状土物理性质指标变化范围，见表3-3-28。

原状土物理性质指标变化范围表3-3-28注：粘砂土3＜I p≤7；砂粘土 7＜I p≤17二、土的平均物理、力学性质指标，见表3-3-29。

土的平均物理、力学性质指标，见表3-3-29。

土的平均物理、力学指标表3-3-29注：①平均比重采取：砂——；粘砂土——；砂粘土——；粘土——；②粗砂和中砂的E 0值适用于不均匀系数C u = = 3者，当C u ＞5时应按表中所列值减少 。

C u为中间值时E 0 值按内插法确定；③对于地基稳定计算，采用人摩擦角φ的计算值低于标准值2°。

三、土的压缩模量一般范围值土的压缩模量一般范围值，见表3-3-3-。

土的压缩模量一般范围值 表3-3-30注：砂粘土7＜I p ≤7；粘土I p ＞17四、粘性土剪强度参考值1060d d 32粘性土抗剪强度参考值，见表3-3-31。

注：粘砂土3＜I p≤7；砂粘土7＜I p≤7；粘土I p＞17五、土的侧压力系数（ξ）和泊松比（u）参考值土的侧压力系数ξ和泊松比u参考值表3-3-32注：粘土I p＞17；粉质粘土10＜I p≤17；I p≤10五、变形模量于压缩模量的关系变形模量E0是指土体在无侧限条件下应力与应变之比，其中的应变包含弹性应变和塑性应变两部分。

因此，变形模量较弹性模量E小，通常在土与基础的共同作用分析中用变形模量E。

变形模量一般是通过现场载荷试验确定，一些地方通过静力触探、标贯试验与变形模量建立了经验公式。

压缩模量Es是在侧限条件下应力与应变的比值，是通过室内试验获取的参数。

两者的关系：对于软土E0近似等于Es；较硬土层，E0=βEs，β=2～8，土愈坚硬，倍数愈大。

土的侧压力系数与泊松比的关系土的侧压力系数和泊松比是土力学中的两个重要物理量，它们之间的关系受到广泛关注。

土的侧压力系数是指土体在垂直于侧面施加的应力作用下，产生的水平反力和垂直反力之比。

泊松比是指材料在一维应力状态下，沿着垂直方向发生压缩应变时产生的侧向应变与垂向应变之比。

从理论上讲，侧压力系数和泊松比的关系应该存在一定的规律性，但具体的关系仍需要实验验证和理论研究。

土的侧压力系数是评价土体在剪切状态下的抗剪强度和变形特性的重要指标之一。

侧压力系数一般用于宏观力学中的岩土力学和土木工程中的土压力计算，它是描述土体抗侧扩张能力的重要参数。

在岩土力学中，侧压力系数可以用来计算土体在侧向应力下产生的各种变形和破坏。

在工程实践中，侧压力系数也广泛应用于巨型土木工程和结构工程的设计和施工。

泊松比是评价土体固结沉降特性的重要指标之一，它是描述土体的变形特性的重要参数。

泊松比反映了材料固有的应变能力，即在某一方向发生压缩应变时，材料沿着垂直方向发生的相应应变。

泊松比在土工、岩土工程、地震工程、机械工程和地质工程等领域的应用十分广泛。

侧压力系数和泊松比之间的关系一直是土力学中的热门话题之一。

在以往的研究中，有许多学者对这两个参数之间的关系进行了深入的探讨。

其中，一些学者指出，侧压力系数和泊松比之间存在一定的相关性，即两者呈负相关关系。

这是因为泊松比越大，土体的压缩能力越强，土体在垂直方向的应变越小，因此土体在侧向应力下的变形越小，侧压力系数也就越大。

反过来说，泊松比越小，土体在侧向应力下的变形越大，因此侧压力系数也会越小。

但是也有一些学者对这种负相关关系提出了质疑，认为侧压力系数和泊松比之间的关系不是单纯的线性关系，而是受到其他因素的影响。

这些因素包括土体的孔隙度、各向异性、饱和状况和含水量等。

因此，在实际工程和科学研究中，应当综合考虑这些因素，进一步探讨侧压力系数和泊松比之间的复杂关系。

总之，侧压力系数和泊松比是岩土力学和土木工程等领域中两个重要的土力学参数，它们之间的关系受到广泛的研究和关注。

土的经验参数(物理指标、压缩、变形模量、剪切强度)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN有关土的经验参数一、原状土物理性质指标变化范围原状土物理性质指标变化范围，见表3-3-28。

注：粘砂土3＜I p≤7；砂粘土 7＜I p≤17二、土的平均物理、力学性质指标，见表3-3-29。

土的平均物理、力学性质指标，见表3-3-29。

注：①平均比重采取：砂——2.66；粘砂土——2.70；砂粘土——2.71；粘土——2.74；②粗砂和中砂的E 0值适用于不均匀系数C u = = 3者，当C u ＞5时应按表中所列值减少 。

C u为中间值时E 0 值按内插法确定；③对于地基稳定计算，采用人摩擦角φ的计算值低于标准值2°。

1060d d 32三、土的压缩模量一般范围值土的压缩模量一般范围值，见表3-3-3-。

注：砂粘土7＜I p≤7；粘土I p＞17四、粘性土剪强度参考值粘性土抗剪强度参考值，见表3-3-31。

注：粘砂土3＜I p≤7；砂粘土7＜I p≤7；粘土I p＞17五、土的侧压力系数（ξ）和泊松比（u）参考值注：粘土I p＞17；粉质粘土10＜I p≤17；I p≤10五、变形模量于压缩模量的关系变形模量E0是指土体在无侧限条件下应力与应变之比，其中的应变包含弹性应变和塑性应变两部分。

因此，变形模量较弹性模量E小，通常在土与基础的共同作用分析中用变形模量E。

变形模量一般是通过现场载荷试验确定，一些地方通过静力触探、标贯试验与变形模量建立了经验公式。

压缩模量Es是在侧限条件下应力与应变的比值，是通过室内试验获取的参数。

两者的关系：对于软土E0近似等于Es；较硬土层，E0=βEs，β=2～8，土愈坚硬，倍数愈大。

土的压缩模量变形模量和弹性模量This model paper was revised by the Standardization Office on December 10, 2020土的压缩模量、变形模量和弹性模量压缩模量、变形模量和弹性模量都是对土的变形能力的不同表达，各自适用于不同情况。

压缩模量Es也叫侧限压缩模量，是土在完全侧限条件（无侧向变形）下，竖向附加应力与相应竖向应变的比值。

其大小反映了土体在单向压缩条件下对压缩变形的抵抗能力。

变形模量Eo是在现场原位测得的，是无侧限条件下应力与应变的比值，相当于理想弹性体的弹性模量，但是由于土体不是理想弹性体，故称为变形模量。

可以比较准确地反映土在天然状态下的压缩性。

压缩模量和变形模量之间可以互相换算，两者间是倍数的关系，土越坚硬倍数越大，软土则两者比较接近。

弹性模量是正应力与弹性（即可恢复）正应变的比值。

在计算饱和粘性土地基上瞬时加荷所产生的瞬时沉降时，就要采用弹性模量。

弹性模量＝应力/弹性应变，它主要用于计算瞬时沉降；压缩模量和变形模量均＝应力/总应变，压缩模量是通过现场取原状土进行实验室有侧限压缩实验得出的，而变形模量则是通过现场的原位载荷试验得出的，它是无侧限的。

弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

地堪报告中，一般给出的是土的压缩模量Es与变形模量Eo，而一般不会给出弹性模量E。

按规范的规定，在地基变形验算中要用的是压缩模量Es，但因Es是通过现场取原状土进行试验的，这对于粘性土来说很容易做到，但对于一些砂土和砾石土等粘聚力较小的土来说，取原状土是很困难的，很容易散掉，因此对砂土的砾石土通常都是通过现场载荷试验得到Eo，所以在地堪报告上，对于砂土的砾石土一般都仅给出Eo，即使给出Es，也是根据Eo换算来的，而不是试验直接得出的。

理论上Es和Eo有一定的关系，但根据该关系换算误差较大，所以二者关系一般都根据地区经验进行换算。

土的压缩模量变形模量和弹性模量Revised by BLUE on the afternoon of December 12,2020.土的压缩模量、变形模量和弹性模量压缩模量、变形模量和弹性模量都是对土的变形能力的不同表达，各自适用于不同情况。

压缩模量Es也叫侧限压缩模量，是土在完全侧限条件（无侧向变形）下，竖向附加应力与相应竖向应变的比值。

其大小反映了土体在单向压缩条件下对压缩变形的抵抗能力。

变形模量Eo是在现场原位测得的，是无侧限条件下应力与应变的比值，相当于理想弹性体的弹性模量，但是由于土体不是理想弹性体，故称为变形模量。

可以比较准确地反映土在天然状态下的压缩性。

压缩模量和变形模量之间可以互相换算，两者间是倍数的关系，土越坚硬倍数越大，软土则两者比较接近。

弹性模量是正应力与弹性（即可恢复）正应变的比值。

在计算饱和粘性土地基上瞬时加荷所产生的瞬时沉降时，就要采用弹性模量。

弹性模量＝应力/弹性应变，它主要用于计算瞬时沉降；压缩模量和变形模量均＝应力/总应变，压缩模量是通过现场取原状土进行实验室有侧限压缩实验得出的，而变形模量则是通过现场的原位载荷试验得出的，它是无侧限的。

弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

地堪报告中，一般给出的是土的压缩模量Es与变形模量Eo，而一般不会给出弹性模量E。

按规范的规定，在地基变形验算中要用的是压缩模量Es，但因Es是通过现场取原状土进行试验的，这对于粘性土来说很容易做到，但对于一些砂土和砾石土等粘聚力较小的土来说，取原状土是很困难的，很容易散掉，因此对砂土的砾石土通常都是通过现场载荷试验得到Eo，所以在地堪报告上，对于砂土的砾石土一般都仅给出Eo，即使给出Es，也是根据Eo换算来的，而不是试验直接得出的。

理论上Es和Eo有一定的关系，但根据该关系换算误差较大，所以二者关系一般都根据地区经验进行换算。

******************************************************************************* 土的变形模量：土的变形模量是通过现场载荷试验求得的压缩性指标，即在部分侧限条件下，其应力增量与相应的应变增量的比值。

土的经验参数(物理指标、压缩、变形模量、剪切强度)有关土的经验参数一、原状土物理性质指标变化范围原状土物理性质指标变化范围，见表3-3-28。

注：粘砂土3＜I p≤7；砂粘土 7＜I p≤17二、土的平均物理、力学性质指标，见表3-3-29。

土的平均物理、力学性质指标，见表3-3-29。

注：①平均比重采取：砂——2.66；粘砂土——2.70；砂粘土——2.71；粘土——2.74；②粗砂和中砂的E 0值适用于不均匀系数C u = = 3者，当C u ＞5时应按表中所列值减少 。

C u为中间值时E 0 值按内插法确定；③对于地基稳定计算，采用人摩擦角φ的计算值低于标准值2°。

1060d d 32三、土的压缩模量一般范围值土的压缩模量一般范围值，见表3-3-3-。

注：砂粘土7＜I p≤7；粘土I p＞17四、粘性土剪强度参考值粘性土抗剪强度参考值，见表3-3-31。

注：粘砂土3＜I p≤7；砂粘土7＜I p≤7；粘土I p＞17五、土的侧压力系数（ξ）和泊松比（u）参考值注：粘土I p＞17；粉质粘土10＜I p≤17；I p≤10五、变形模量于压缩模量的关系变形模量E0是指土体在无侧限条件下应力与应变之比，其中的应变包含弹性应变和塑性应变两部分。

因此，变形模量较弹性模量E小，通常在土与基础的共同作用分析中用变形模量E。

变形模量一般是通过现场载荷试验确定，一些地方通过静力触探、标贯试验与变形模量建立了经验公式。

压缩模量Es是在侧限条件下应力与应变的比值，是通过室内试验获取的参数。

两者的关系：对于软土E0近似等于Es；较硬土层，E0=βEs，β=2～8，土愈坚硬，倍数愈大。

土的压缩模量变形模量和弹性模量The latest revision on November 22, 2020土的压缩模量、变形模量和弹性模量压缩模量、变形模量和弹性模量都是对土的变形能力的不同表达，各自适用于不同情况。

压缩模量Es也叫侧限压缩模量，是土在完全侧限条件（无侧向变形）下，竖向附加应力与相应竖向应变的比值。

其大小反映了土体在单向压缩条件下对压缩变形的抵抗能力。

变形模量Eo是在现场原位测得的，是无侧限条件下应力与应变的比值，相当于理想弹性体的弹性模量，但是由于土体不是理想弹性体，故称为变形模量。

可以比较准确地反映土在天然状态下的压缩性。

压缩模量和变形模量之间可以互相换算，两者间是倍数的关系，土越坚硬倍数越大，软土则两者比较接近。

弹性模量是正应力与弹性（即可恢复）正应变的比值。

在计算饱和粘性土地基上瞬时加荷所产生的瞬时沉降时，就要采用弹性模量。

弹性模量＝应力/弹性应变，它主要用于计算瞬时沉降；压缩模量和变形模量均＝应力/总应变，压缩模量是通过现场取原状土进行实验室有侧限压缩实验得出的，而变形模量则是通过现场的原位载荷试验得出的，它是无侧限的。

弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

地堪报告中，一般给出的是土的压缩模量Es与变形模量Eo，而一般不会给出弹性模量E。

按规范的规定，在地基变形验算中要用的是压缩模量Es，但因Es是通过现场取原状土进行试验的，这对于粘性土来说很容易做到，但对于一些砂土和砾石土等粘聚力较小的土来说，取原状土是很困难的，很容易散掉，因此对砂土的砾石土通常都是通过现场载荷试验得到Eo，所以在地堪报告上，对于砂土的砾石土一般都仅给出Eo，即使给出Es，也是根据Eo换算来的，而不是试验直接得出的。

理论上Es和Eo有一定的关系，但根据该关系换算误差较大，所以二者关系一般都根据地区经验进行换算。

********************************************************************* **********土的变形模量：土的变形模量是通过现场载荷试验求得的压缩性指标，即在部分侧限条件下，其应力增量与相应的应变增量的比值。

静止侧压力系数K0参考值土类液限w L塑性指数静止侧压力系数K0饱和松砂0.46饱和紧砂0.34干紧砂（e=0.6）0.49干松砂（e=0.6）0.64压实残积黏土9 0.42压实残积黏土74% 31 0.66原状有机质土61% 45 0.57原状高岭土37% 23 0.64~0.70原状海相黏土34% 16 0.48灵敏性黏土10 0.52泊松比v的参考值弹性模量E的参考值在弹性阶段，E=Eo＝Es（1-2μ^2/(1-μ)），土力学上有相关说明。

有经验说是E=（2~5）·Es（未考证出处）变形模量的定义在表达式上和弹性模量是一样的E=ζ/ε，对于变形模量ε是指应变，包括弹性应变εe和塑性应变εp，对于弹性模量而言，ε就是指εe(计算变形模量时，应变ε包括了弹性应变和塑性应变)。

岩土的弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

弹性模量>压缩模量>变形模量。

弹性模量也叫杨氏模量（岩土体在弹性限度内应力与应变的比值）压缩模量是有侧限的，杨氏模量是无侧限的。

同样的土体，同样的荷载，有侧限的土体应变小，所以压缩模量更大才对。

这只是弹性理论上的关系，对土体这种自然物不一定适用。

土体计算中所用的称为“弹性模量”不一定是在弹性限度内。

E——弹性模量；Es——压缩模量；Eo——变形模量。

弹性模量＝应力/弹性应变，它主要用于计算瞬时沉降。

压缩模量和变形模量均＝应力/总应变。

压缩模量是通过现场取原状土进行实验室有侧限压缩实验得出的，而变形模量则是通过现场的原位载荷试验得出的，它是无侧限的。

弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

地堪报告中，一般给出的是土的压缩模量Es与变形模量Eo，而一般不会给出弹性模量E。

数值模拟中一般用Eo，E（50），达到峰值应力（应变）50％时的割线模量。

Es（勘查报告中提供），有侧限，E＝2.0～5.0Es（看别人这么弄的）。

土的变形模量与压缩模量的关系土的变形模量和压缩模量，是判断土的压缩性和计算地基压缩变形量的重要指标。

为了建立变形模量和压缩模量的关系，在地基设计中，常需测量土的侧压力系数0K 和侧膨胀系数（泊松比）μ。

侧压力系数0K ：是指侧向压力x σ与竖向压力z σ之比值，即：0K ＝x σ/z σ土的侧膨胀系数（泊松比）μ：是指在侧向自由膨胀条件下受压时，侧向膨胀的应变x ε与竖向压缩的应变z ε之比值，即：μ＝x ε/z ε根据材料力学广义胡克定律推导求得0K 和μ的相互关系：0K ＝μ/(1－μ)或μ=0K /（1＋0K ）土的侧压力系数可由专门仪器测得，但侧膨胀系数不易直接测定，可根据土的侧压力系数，按上式求得。

在土的压密变形阶段，假定土为弹性材料，则可根据材料力学理论，推导出变形模量0E 和压缩模量S E 之间的关系。

数值计算时应用土体的变形模量。

令β＝2121μμ-- 则0E ＝β×S E当μ＝0～0.5时，β＝1～0，即0E /S E 的比值在0～1之间变化，即一般0E 小于S E 。

但很多情况下0E /S E 都大于1。

其原因为：一方面是土不是真正的弹性体，并具有结构性；另一方面就是土的结构影响；三是两种试验的要求不同。

注：0E 与S E 之间的关系是理论关系，实际上，由于各种因素的影响，0E 值可能是β×S E 值的几倍，一般来说，土愈坚硬则倍数愈大，而软土的0E 值与β×S E 值比较。

弹性模量E指材料在弹性变形范围内（即在比例极限内），作用于材料上的纵向应力与纵向应变的比例常数。

也常指材料所受应力（如拉伸，压缩，弯曲，扭曲，剪切等）与材料产生的相应应变之比。

对均质土体而言，弹性模量与压缩模量之间有如下关系：()11(12)S E E μμμ-=+-，或(1)(12)1S E E μμμ+-=-2211S E μμ⎛⎫=- ⎪-⎝⎭上海地区土体的弹性模量一般为压缩模量的3～5倍，即：3~5S E E =变形模量0E土的变形模量是通过现场载荷试验求得的压缩性指标，即在部分侧限条件下，其应力增量与相应的应变增量的比值（土的变形模量是土体在无侧限条件下应力与应变之比值），由于土体不是理想的弹性体，故称为变形模量。

天然土或人工填土中任何一点的水平有效应力与竖向有效应力之比称改土的侧压力系数K。

如果土体在承受竖向压力时，不允许产生侧向变形，这时的侧压力则称为静止侧压力，相应的系数称静止侧压力系数，以K0表示。

实际工程常遇到上述K0状态的应力，例如房屋地下室外墙面、重力式挡墙无横向位移时的墙背，以及船闸的墙所受土压力皆为静止土压力。

对于正常固结黏土或砂土K0＝1-sinφ‘ ；对于超固结土，按下式估算K0＝(1-sinφ‘)(OCR)^sinφ φ‘为土的有效内摩擦角，OCR为超固结比。

静止侧压力系数K0与泊松比ν及弹性模量E的理论关系分别为：K0＝ν/(1-ν) ；E=(1-2K0)(1+K0)/[Mv(1-K0)] E为弹性模量(kpa)，Mv为体积压缩系数。

正常固结沉积黏土的K0一般介于0.4～0.7之间，砂土约为0.4。

自然沉积超固结土的水平应力可以大于竖向方向应力，故K0常大于1.0，可以达到3.1.静止侧压力系数K0的参考值：饱和松砂0.46、饱和紧砂0.34、干紧砂(e=0.6) 0.49、干松砂(e=0.8)0.64、原状有机质淤泥0.57 、原状高岭土0.64～0.70 、原状海相黏土0.48 、灵敏性黏土0.52 。

静止侧压力系数K0参考值土类液限w L塑性指数静止侧压力系数K0饱和松砂0.46饱和紧砂0.34干紧砂（e=0.6）0.49干松砂（e=0.6）0.64压实残积黏土9 0.42压实残积黏土74% 31 0.66原状有机质土61% 45 0.57原状高岭土37% 23 0.64~0.70原状海相黏土34% 16 0.48灵敏性黏土10 0.522.泊松比ν的参考值：饱和黏土0.5、含砂和粉土的黏土0.3～0.42 、非饱和黏土0.35～0.40、黄土0.44、砂质土0.15～0.25、砂土0.30～0.35泊松比v的参考值3.弹性模量E的参考值（MN×ｍ^-2）很软的黏土0.35～3、软黏土2～5、中硬黏土4～8、硬黏土7～18、砂质黏土30～40、粉质黏土7～20、松砂10～25、紧砂50～80、紧密砂、卵石100～200 。

土的变形模量是土体在无侧限条件下应力与应变之比值，相当于弹性模量。

由于土体不是理想的弹性体，故称为变形模量。

土的变形模量反映了土体抵抗弹塑性变形的能力，可用于弹塑性问题分析，通常可以通过三轴试验或现场试验进行测定。

如果现场原位试验未进行，可以通过其他方法进行估算、假定或理论计算。

E－－弹性模量Es－－压缩模量Eo－－变形模量在工程中土的弹性模量要远大于压缩模量和变形模量，而压缩模量又大于变形模量。

但在勘察报告中却只提供变形模量，在模拟计算的时侯我们要用弹性模量。

变形模量的定义在表达式上和弹性模量是一样的E=ζ/ε，对于变形模量ε是指应变，包括弹性应变εe和塑性应变εp，对于弹性模量而言，ε就是指εe。

压缩模量指的是侧限压缩模量，通过固结试验可以测定。

如果土体是理想弹性体，那么E＝Es（1-2μ^2/(1-μ)）＝E0。

在土体模拟分析时，如果时一维压缩问题，选用Es；如果是变形问题，一般用E0；如果是瞬时变形，或弹性变形用E。

土的变形模量和压缩模量，是判断土的压缩性和计算地基压缩变形量的重要指标。

为了建立变形模量和压缩模量的关系，在地基设计中，常需测量土的側压力系数ξ和側膨胀系数μ。

側压力系数ξ：是指側向压力δx与竖向压力δz之比值，即：ξ＝δx/δz土的側膨胀系数μ（泊松比）：是指在側向自由膨胀条件下受压时，测向膨胀的应变εx与竖向压缩的应变εz之比值，即μ＝εx/εz根据材料力学广义胡克定律推导求得ξ和μ的相互关系，ξ＝μ/(1－μ)或μ＝ε/（1＋ε）土的側压力系数可由专门仪器测得，但側膨胀系数不易直接测定，可根据土的側压力系数，按上式求得。

在土的压密变形阶段，假定土为弹性材料，则可根据材料力学理论，推导出变形模量E0和压缩模量Es之间的关系。

，令β＝则Eo＝βEs当μ＝0～0.5时，β＝1～0，即Eo/Es的比值在0～1之间变化，即一般Eo小于Es。

但很多情况下Eo/Es 都大于1。

其原因为：一方面是土不是真正的弹性体，并具有结构性；另一方面就是土的结构影响；三是两种试验的要求不同；μ、β的理论换算值土的种类μβ碎石土0.15～0.20 0.95～0.90砂土0.20～0.25 0.90～0.83粉土0.23～0.31 0.86～0.72粉质粘土0.25～0.35 0.83～0.62粘土0.25～0.40 0.83～0.47注：E0与Es之间的关系是理论关系，实际上，由于各种因素的影响，E0值可能是βEs值的几倍，一般来说，土愈坚硬则倍数愈大，而软土的E0值与βEs值比较。

土的变形模量与压缩模量的关系土的变形模量和压缩模量，是判断土的压缩性和计算地基压缩变形量的重要指标。

为了建立变形模量和压缩模量的关系，在地基设计中，常需测量土的侧压力系数0K 和侧膨胀系数（泊松比）μ。

侧压力系数0K ：是指侧向压力x σ与竖向压力z σ之比值，即：0K ＝x σ/z σ 土的侧膨胀系数（泊松比）μ：是指在侧向自由膨胀条件下受压时，侧向膨胀的应变x ε与竖向压缩的应变z ε之比值，即：μ＝x ε/z ε根据材料力学广义胡克定律推导求得0K 和μ的相互关系：0K ＝μ/(1－μ)或μ=0K /（1＋0K ）土的侧压力系数可由专门仪器测得，但侧膨胀系数不易直接测定，可根据土的侧压力系数，按上式求得。

在土的压密变形阶段，假定土为弹性材料，则可根据材料力学理论，推导出变形模量0E 和压缩模量S E 之间的关系。

数值计算时应用土体的变形模量。

令β＝2121μμ--则0E ＝β×S E当μ＝0～0.5时，β＝1～0，即0E /S E 的比值在0～1之间变化，即一般0E 小于S E 。

但很多情况下0E /S E 都大于1。

其原因为：一方面是土不是真正的弹性体，并具有结构性；另一方面就是土的结构影响；三是两种试验的要求不同。

注：0E 与S E 之间的关系是理论关系，实际上，由于各种因素的影响，0E 值可能是β×S E 值的几倍，一般来说，土愈坚硬则倍数愈大，而软土的0E 值与β×S E 值比较。

弹性模量E指材料在弹性变形范围内（即在比例极限内），作用于材料上的纵向应力与纵向应变的比例常数。

也常指材料所受应力（如拉伸，压缩，弯曲，扭曲，剪切等）与材料产生的相应应变之比。

对均质土体而言，弹性模量与压缩模量之间有如下关系：()11(12)S E E μμμ-=+-，或(1)(12)1S E E μμμ+-=-2211S E μμ⎛⎫=- ⎪-⎝⎭上海地区土体的弹性模量一般为压缩模量的3～5倍，即：3~5S E E =变形模量0E土的变形模量是通过现场载荷试验求得的压缩性指标，即在部分侧限条件下，其应力增量与相应的应变增量的比值（土的变形模量是土体在无侧限条件下应力与应变之比值），由于土体不是理想的弹性体，故称为变形模量。

静止土压力系数与泊松比的关系推导1. 引言大家好，今天咱们聊聊一个看似复杂但其实挺有趣的话题——静止土压力系数和泊松比的关系。

听上去有点高大上对吧？别担心，咱们慢慢来，把这个“土”字给弄明白，保证让你听得懂，也能笑着学到新东西。

首先，静止土压力系数，简单说就是在土壤静止状态下，土对结构的压力大小。

而泊松比嘛，呵呵，这个词可能让你联想到科学家在黑板上划来划去的样子，但其实它就是描述材料在受力时，横向和纵向变形的比例。

没错，就是这么简单！1.1 土压力的概念说到土压力，想象一下你在海边玩沙子，往沙子里插根小旗子。

随着你在沙子里推、压，小旗子旁边的沙子是不是也会被挤动？这就类似于土压力的概念。

当有结构在土壤上方时，土壤就会施加压力，就像小旗子被挤压的那一刻，给你一种“土有脾气”的感觉。

土壤可不是无情的，它对上面的建筑可是一点也不含糊，压力大小可和它的状态、性质密切相关。

1.2 泊松比的理解而泊松比就像是土壤的性格，咱们可以把它想象成一个小魔术师。

当你施加力量，土壤在某个方向上发生变形的时候，它总是忍不住在另外一个方向“反击”，这就是泊松比的来由。

比如你捏一块橡皮泥，它会变得扁扁的，但宽度会相应增大，横纵之间的变化比例就是它的泊松比。

有趣吧？2. 土压力系数与泊松比的关系2.1 理论推导那么，这两者之间到底有什么关系呢？在静止的状态下，土的压力就会受到泊松比的影响。

咱们可以这样想：如果土壤的泊松比大，意味着它在受到压力时，横向扩展的能力很强，导致它能承受的静止土压力就会更大。

换句话说，土壤越“丰满”，它对压力的抵抗能力就越强，静止土压力系数就越高，真是个“胖子”的优越性嘛！2.2 实际应用在实际工程中，这个关系可大有用处，比如在建筑设计的时候，咱们常常需要考虑土壤的性质来选择合适的材料。

如果泊松比过高，可能意味着土壤在受力后会有很大的侧向位移，这时候就得特别小心了，否则可真是“掉了脑袋”的事儿。

工程师们必须考虑到这些细节，才能避免在施工时碰到大麻烦。