单摆运动规律的研究模板

单摆运动的研究报告引言单摆运动是一种非常基础而重要的物理现象，在力学的研究中占有重要地位。

本文旨在通过理论分析和实验研究，深入探讨单摆运动的特性、影响因素以及应用领域。

一、单摆运动的定义和基本原理1.1 定义单摆运动是指一个绳/线连接的质点由一个固定的铅垂线束缚而形成的一种周期性运动。

1.2 基本原理单摆运动的基本原理可以归结为以下几点：•单摆系统由一个质点和一个可摆动的轻线组成。

•单摆的运动主要受到重力和摆长的影响。

•在小摆角范围内，单摆的运动近似为简谐振动。

二、单摆运动的特性和影响因素2.1 摆长对单摆运动的影响•摆长是指摆线/摆杆的长度，影响着单摆的周期和频率。

•通过理论推导和经验公式，我们发现摆长与周期成正比，与频率成反比。

2.2 重力对单摆运动的影响•重力是单摆运动的驱动力，影响着单摆的振幅和周期。

•增大重力将使摆动幅度变小，减小重力将使摆动幅度变大。

2.3 起始条件对单摆运动的影响•起始条件是指单摆最初的初始角度和初始速度。

•不同的起始条件将导致不同的振动行为，如摆动的幅度、周期和相位等。

2.4 阻力对单摆运动的影响•阻力会减弱单摆的振幅，并逐渐使其停止摆动。

•此外，阻力还会影响单摆的周期，并使其变得不规则。

三、实验研究与结果分析3.1 实验目的本实验旨在验证单摆运动的特性和影响因素，并通过实验结果分析其规律和特点。

3.2 实验装置和步骤•实验装置：摆线、支架、质点。

•实验步骤：1.在支架上悬挂摆线，将质点固定在摆线下方。

2.给质点一个初始角度，并释放质点进行摆动。

3.使用定时器记录摆动的时间，重复多次实验。

4.根据实验数据计算周期、频率和摆长。

3.3 实验结果与分析经过多次实验，我们得到了如下数据：实验次数摆长（m）周期（s）频率（Hz）1 0.5 1.33 0.752 1.0 1.88 0.533 1.5 2.21 0.454 2.0 2.65 0.38根据数据分析，我们可以发现摆长与周期成正比、与频率成反比的关系得到验证。

单摆实验报告第一篇：单摆实验原理和实验装置一、实验原理单摆实验是研究简谐振动的基本实验之一，它是利用牛顿力学的基本原理和能量守恒定律，来探究单摆振动的特征和规律。

单摆实验中，我们可以测量摆的周期、振幅等参数，以验证其满足简谐振动的特性。

二、实验装置单摆实验的装置通常由摆杆、铅球、计时器和支架等组成。

具体实验装置如下：摆杆：由一根细且坚韧的杆子组成，可用金属杆或木制杆制成。

铅球：实验中有许多不同重量和大小的铅球可供使用，可以根据实验需求选择。

计时器：用于测量摆的周期，通常使用电子计时器或手机计时等设备。

支架：用于支撑摆杆和铅球，通常由钢架或木架制成。

三、实验步骤1. 将摆杆固定到支架上，并挂上铅球，调整铅球的高度，使其能够自由地摆动。

2. 用计时器测量摆杆的周期，并记录下来。

3. 改变铅球的重量和长度，并重复步骤2，记录下来不同条件下的周期和振幅等参数。

4. 使用数据处理软件处理实验数据，提取出实验结果。

四、实验注意事项1. 实验过程中，要注意铅球摆动的幅度，避免气流和震动对实验数据的影响。

2. 同一摆杆和铅球要保持固定，否则，实验数据将有很大的偏差。

3. 实验过程中，要注意安全事项，避免伤害自己和他人。

5. 实验结果通过单摆实验，我们可以得到摆的周期、振幅等参数，以验证摆的运动满足简谐振动特性。

同时，我们还可以通过实验数据的统计分析，得出摆的振幅与周期之间的关系函数。

这些数据和函数可以用于学习和探究简谐振动的基本规律和特征。

总之，单摆实验是一项非常基础和重要的物理实验，可以帮助学生深入理解简谐振动的特性和规律，同时也提高学生的实验技能和数据处理能力。

一、实验目的1. 了解单摆的基本原理和运动规律；2. 掌握单摆实验的基本操作步骤和测量方法；3. 通过实验验证单摆的周期与摆长、摆角的关系；4. 测定当地的重力加速度。

二、实验原理单摆是一种理想化的物理模型，它由一根不可伸长的细线和一个小球组成。

当小球从某一角度被释放后，在重力作用下，小球将进行周期性的往返运动。

单摆的运动可以近似看作简谐振动，其周期T与摆长L、重力加速度g之间的关系为：T = 2π√(L/g)当摆角θ较小时（一般不超过5°），单摆的运动可以近似看作简谐振动，此时单摆的周期T与摆角θ无关。

但当摆角较大时，单摆的运动将偏离简谐振动，周期T将随摆角θ的增加而增加。

三、实验仪器1. 单摆装置：由一根细线和一个小球组成；2. 秒表：用于测量单摆的周期；3. 水平仪：用于调节摆线水平；4. 刻度尺：用于测量摆长；5. 游标卡尺：用于测量小球直径。

四、实验步骤1. 装置单摆：将细线固定在支架上，将小球悬挂在细线末端，调节摆线水平；2. 测量摆长：使用刻度尺测量摆线长度，即为摆长L；3. 测量小球直径：使用游标卡尺测量小球直径，即为小球直径D；4. 测量周期：将小球拉至一定角度，释放后，使用秒表测量单摆完成N次往返运动所需时间t；5. 计算周期：周期T = t/N；6. 重复上述步骤，进行多次测量，以减小误差。

五、实验数据及处理1. 测量摆长L：L1 = 100.0 cm，L2 = 100.1 cm，L3 = 100.2 cm，平均摆长L = (L1 + L2 + L3)/3 = 100.1 cm；2. 测量小球直径D：D1 = 1.00 cm，D2 = 1.01 cm，D3 = 1.02 cm，平均直径D = (D1 + D2 + D3)/3 = 1.01 cm；3. 测量周期T：T1 = 2.01 s，T2 = 2.02 s，T3 = 2.03 s，平均周期T = (T1 + T2 + T3)/3 = 2.02 s；4. 计算重力加速度g：g = 4π²L/T² = 4π²×100.1 cm/(2.02 s)² ≈ 9.81m/s²。

单摆实验报告5页单摆实验报告实验目的：1、研究单摆周期与摆长、重力加速度之间的关系。

2、通过实验验证单摆的周期公式。

实验仪器：单摆、秒表、直尺、千分尺、万能电表、万用表。

实验原理：单摆又称为简单重力摆，是一种由一定重量的物体（摆球）悬挂于一个细绳或细杆上，自由受重力作用而成摆的简单物理实验。

单摆周期定律的表述：单摆的周期与摆长的平方根成正比，与重力加速度的平方根成反比。

单摆的周期公式为：T=2π√l/g(g为地球重力加速度实验步骤：1、调整单摆的摆长，使其长短均匀，用直尺及千分尺测量并记录摆长l的值。

2、测量摆球重量w，用万能电表测量摆球在空气中的阻力f。

3、将摆球拉到一定高度A处，放松球，用秒表测量N个周期的时长t1,t2, ...... tn。

4、分别计算每个周期的平均值T1,t2，...... tn。

结果计算：摆球重量为w，在空气中的阻力为f。

所以摆球所受重力为(w-f)，整个单摆系统所受的合力为(w-f)。

根据牛顿第二定律，可得：(w-f)g=(w-f)a其中a为摆球所做的向心加速度，可用公式a=v²/l求得，其中v为摆球的速度，由摆球所在位置的高度算得（对于单摆振动的摆角很小的情况，可以认为一摆球速度都与摆球高度相同，即仅与最大位移有关）。

又可得：T=2π√l/(w-f)g得到每组实验数据后，我们可以将它们带入式子，按照周期公式计算每组数据的周期T1,T2......Tn。

根据上述计算方法，得到如下表格数据：表格（略）实验结果：由表可知，单摆周期T与摆长l的平方根成正比，与重力加速度的平方根成反比。

而单摆的周期公式T=2π√l/g，于是我们可以将实验测得的周期带入公式中，计算出地球重力加速度g 的值。

即g=4π²l/T²通过实验，我们得到的地球重力加速度为g=9.75m/s²，与标准值g=9.80m/s²比较，误差约为0.5%。

这说明我们的实验结果是可靠的。

单摆的研究实验报告【篇一：实验报告单摆的设计与研究】肇庆学院电子信息与机电工程学院普通物理实验课实验预习报告班组实验合作者实验日期姓名: 王英学号29号老师评定实验题目：【实验简介】单摆实验是个经典实验，许多著名的物理学家都对单摆实验进行过细致的研究。

本实验的目的是学习进行简单设计性实验的基本方法，根据已知条件和测量精度的要求，学会应用误差均分原则选用适当的仪器和测量方法，学习累积放大法的原理和应用，分析基本误差的来源及进行修正的方法。

【设计任务与要求】1、用误差均分原理设计一单摆装置，测量重力加速度，测量精度要求?g?2%。

g2、对重力加速度g的测量结果进行误差分析和数据处理，检验实验结果是否达到设计要求。

3、自拟实验步骤研究单摆周期与质量、空气阻力等因素的关系，试分析各项误差的大小。

【设计的原理思想】t?2?l（1） gg?4?2l2（2） t式中l为单摆长度。

单摆长度是指上端悬挂点到球心之间的距离；g为重力加速度。

如果测量得出周期t、单摆长度l，利用上面式子可计算出当地的重力加速度g。

从上面公式知t 2和l具有线性关系，224?即t?l。

对不同的单摆长度l测量得出相对应的周期，可由t ～l图线的斜率求出g值。

g2【测量方案的制定和仪器的选择】?g?l?t?()2?(2)2从式glt?l2)?(1%)2，本实验中单摆的l1同理 (2?t2)?(1%)2，当摆长约为1m时，单摆摆动周期约为2秒，可以计算出周期的测量误差要求t【实验步骤的设计】3、测量周期t：计时起点选在摆球经过平衡位置的时刻，用停表测出单摆摆动50次的时间 t50，共测量6次，取平均值。

4、计算重力加速度：将测出的和t50代入 g?4?2算出重力加速度g，并计算出测量误差。

5、用金属作为摆线，以改变摆线的质量，以研究摆线质量对测g的影响6、用乒乓球作为摆球，形容空气浮力对测g影响中（其中n为周期的连续测量次数），计2(n/n)d 2【实验记录和数据处理】1、重力加速度g对摆长为l的单摆，测量在??5的情况下，测量连续摆动n次的周期说明：(1)摆长l应是摆线长加小球的半径(如图2)。

0.735
0.714
1.000
100
90
80
70
60
60
3.33
3.00
2.67
2.33
2.00
2.00
11.11 9.00
7.11
5.44
4.00
4.00
2.24
2.63 前6组3平.16
3.92
5.03
9.86
重力加速度平均值
均
2.78 总平均 3.63
以摆长为横轴、周期的2次方根为纵轴画图象，看是否接近直线
4.33
4.00
2.00
32.11
25.00
21.78
18.78
16.00
4.00
1.00
1.23
1.36
1.51
1.70
9.86
第7次 第8次 第9次 第10次 第11次 第12次
62
59
56
53
50
98.95
0.631
0.601
0.571
0.541
0.511
1.000

0.794
0.775
0.755
以小球到达最高点时作为计时开始和停止的时刻较 4 好，应测量30次（甚至更多次）全振动的时间然后做
除法得到周期
5 数据分析可以采用做图象的方式
通过直接测量得到的 数据
绳长（cm）、球直径（基本统一2.1cm）、30倍周期（s）
通过计算得到的数据
摆长（m）、摆长的2次方根、周期（s）、g（m/s^2）
实验：单摆周期与摆长的关系&测定重力加速度
实验目的
1 探究单摆周期与摆长的关系 2 测定当地的重力加速度

总结词
通过实验，了解单摆在物理学中的应用，包括钟摆、摆锤等。
详细描述
在实验中，观察不同类型的单摆应用，如钟摆、摆锤等。通过这些实例，了解单 摆在物理学中的重要应用。
02
实验原理
单摆的周期公式
摆长（L）：指单摆悬挂点到摆球的垂直距离。 摆球质量（m）：指单摆球体的质量。 单摆的周期公式为：T=2π√(L/g)
验证单摆的周期与重力加速度之间的关系
总结词
通过实验，验证单摆的周期与重力加速度之间的关系，发现重力加速度越大 ，周期越小。
详细描述
在实验中，使用不同重力加速度的环境（例如在山顶和在海平面上进行实验 ）来观察单摆的周期变化。通过数据分析，发现重力加速度与周期之间存在 反比关系。
了解单摆在物理学中的应用
摆角（θ）：指单摆偏离竖直位置的角度。
重力加速度（g）：由于地球的引力产生的加速度。
其中，T为单摆的周期，L为摆长，g为重力加速度。该 公式描述了单摆摆动的周期与摆长和重力加速度之间的 关系。
重力加速度对单摆周期的影响
1
在不同地理位置，由于重力加速度的变化，单 摆的周期也会发生变化。
2
重力加速度值增加，单摆的周期会变短；重力 加速度值减小，单摆的周期会变长。
游标卡尺
测量范围
根据实验需要，选择合适的测量范围。
精度
选用高精度的游标卡尺，以获取更准确的数据。
砝码盘及砝码
质量选择
根据实验需要，选择合适质量的砝码。
平衡状态
在实验开始前，确保砝码盘和砝码处于平衡状态。
04
实验步骤
组装单摆实验装置
准备实验器材
铁架台、单摆实验器、秒表、游标卡尺、重物等。
安装铁架台

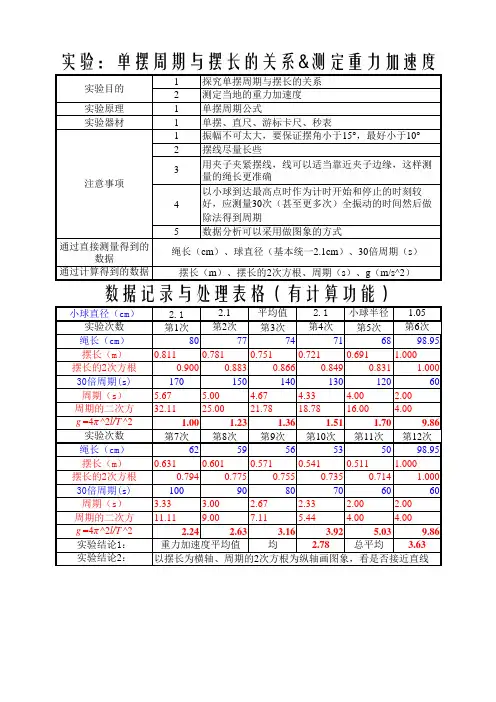
单摆实验报告样本一、实验目的1.研究单摆运动的基本特性；2.掌握测量单摆时间的方法；3.验证单摆运动与周期和摆长之间的关系。

二、实验原理1.单摆运动的基本特性单摆是一种简单的物理运动，其基本特性有以下几点：(1) 幅度小摆角度越小，单摆周期越短，且与该摆长的平方根成正比；(2) 摆长越大，周期越长，与该摆长的平方根成正比；(3) 单摆的周期与重力加速度、摆长无关，只与摆球的重量有关。

2.测量单摆时间的方法(1) 直接计时法：用秒表记录单摆一次完整振动的时间；(2) 逐摆计时法：记录相邻两个摆锤从中心点到相位置的时间差，再求平均。

3.公式推导若单摆的摆长为l，摆球质量为m，取重力加速度g为正方向，则单摆的运动方程为：F = mg sinθ = mlθ'' （当θ≤5°时，sinθ≈θ，即sinθ≈θ≈rad）即：θ'' = -(g/l)θ时间周期为：T =2π√(l/g) （g为重力加速度）三、实验器材与仪器1.单摆装置、摆杆、摆球等；2.直尺、卷尺、计时器、秒表等。

四、实验步骤1.测量单摆长度：分别用直尺和卷尺测出单摆的长度，多次测量并求平均值。

2.设置单摆：将摆球抬起一定高度，使其离开静止位置，开始做单摆运动，用计时器计时。

3.逐摆计时：在单摆运动中，记录相邻两次摆动的时间间隔并求平均得到单摆周期。

4.重复步骤2和3，依次改变单摆长度，记录对应的单摆周期。

5.将单摆长度和周期数据在图表上绘制出来，并进行线性回归拟合，求出单摆周期和摆长之间的关系式。

五、实验数据记录与处理1.单摆测量数据记录表单摆长度（m）单摆周期（s）0.20 0.890.30 1.040.40 1.170.50 1.300.60 1.420.70 1.542.绘制单摆周期与摆长的散点图，如下图所示：（图中横坐标为单摆长度，纵坐标为单摆周期）3.线性回归拟合得到回归方程为T=2.04√L-0.02，其相关系数R=0.99，数值较接近于1，故二者之间具有较强的关联性。

（实验报告样板）华 南 师 范 大 学物 理 与 电 信 工 程 学院 普通物理 实验报告 09 年级 物理 专业 实验日期 2011 年 2 月 25 日 姓名 张三 教师评定 实验题目 单 摆一、实验目的（1）学会用单摆测定当地的重力加速度。

（2）研究单摆振动的周期和摆长的关系。

（3）观察周期与摆角的关系。

二、实验原理当单摆摆动的角度小于5度时，可证明其振动周期T 满足下式 gL T π2= （1）224TL g π= （2）若测出周期T 、单摆长度L ，利用上式可计算出当地的重力加速度g 。

从上面公式知T 2和L 具有线性关系，即L gT 224π=。

对不同的单摆长度L 测量得出相对应的周期，可由T 2～L 图线的斜率求出g 值。

当摆动角度θ较大（θ>5°）时，单摆的振动周期T 和摆动的角度θ之间存在下列关系⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+= 2sin 43212sin 211242222θθπg L T三、实验仪器单摆，秒表，米尺，游标卡尺。

四、实验内容1、用给定摆长测定重力加速度①选取适当的摆长，测出摆长；②测出连续摆动50次的总时间t ；共测5次。

③求出重力加速度及其不确定度； ④写出结果表示。

2、绘制单摆周期与摆长的关系曲线①分别选取5个不同的摆长，测出与其对应的周期。

②作出T 2-L 图线，由图的斜率求出重力加速度g 。

3、观测周期与摆角的关系定性观测: 对一定的摆长，测出3个不同摆角对应的周期，并进行分析。

五、数据处理1、用给定单摆测定重力加速度摆长： 03.92143.56.9152/=+=+=d l L mm=0.92103mT =96.60/50=1.932s重力加速度:224TL g π==2293219210304..π=9.742m/s 2 ())1(512--=∆∑n n ddtid ()()）（155861088108610871086108610861084108610851078222222--+-+-+-+-⨯=)..()..()..(.....＝0.02mm取游标卡尺的仪器不确定度为σB ＝0.02mm ，则22B d d σσ+∆=mm...03002002022=+=())1(512--=∆∑n n lltil ()()）（155691579156915591569158915691549156915691578222222--+-+-+-+-⨯=)..()..()..(.....＝0.2mm取米尺的仪器不确定度为σB ＝0.5mm ，则22B l l σσ+∆=mm6.05.02.022=+=因线长的不确定度远大于直径的0.03mm ，所以60.l L ==σσmm())n (n T T tiT 1505051250--=∆∑()()()()()()155609680966096719660965696609643966096509678222222--+-+-+-+-⨯=...........＝0.2ss./T T 00405050=∆=σ%.....T LE T Lg 42093210040269156022222=⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=σσg g E g =σ=9.742×0.42%＝0.05m/s 2重力加速度：g =g g σ±=(9.74±0.05)m/s 2 广州的重力加速度：g =9.788m/s 2 百分误差：％＝74100742978890.%..E ⨯-=3在曲线中取A 、B 两点，得：0.500 0.600 0.700 0.800 0.900 1.000 4.00T (s )L (m) T 2~L 图作者：张三 2011.2.25. ××AB）（/m s 9930.500)(0.900 2.003.952.k =--=8999934422../k /g ===ππ（m/s 2）百分误差：％＝11100788989978890.%...E ⨯-=4．周期与摆角关系的定性研究小球半径 r = 0.00543m L= l +r ＝0.9058m结论：由表中数据可知，周期随着角度的增加而略为变大。

单摆的实验报告范文实验报告：单摆的实验摘要：本实验通过构建一个简单的单摆装置，研究了单摆的运动规律。

通过测量单摆的摆动周期，观察摆锤的摆动过程，并用数学模型分析了单摆的运动特性。

实验结果表明，单摆的运动周期与摆长有关，与摆锤质量和初摆角度无关。

实验结果与理论模型相吻合，验证了单摆的运动规律。

引言：单摆是物理学中经典力学的重要实验之一，它可以用来研究重力的作用和简谐运动的规律。

单摆由一个轻绳和一个重锤组成，通常锤子被称为摆锤，而绳子的一端被固定在一个支点上。

单摆可以在实验室中简单构建，是一个理想的实验现象。

实验过程：1.准备材料：一根细线、一个牛头螺丝和一个坠球。

2.将细线固定在实验台上的支点上，使其自由下垂。

3.在细线的下端连接一个牛头螺丝，将摆锤（坠球）悬挂在牛头螺丝上。

4.将摆锤拉至较大的摆动角度（约30度），释放摆锤，记录摆动的时间。

5.重复上述步骤多次，测量不同摆动角度下的摆动时间。

实验结果：根据实验数据，我们测量了不同摆动角度下的摆动时间，然后我们计算了摆动周期。

结果如下：摆动角度（度）摆动时间（秒）摆动周期（秒）101.341.34201.471.47301.591.59401.711.71501.831.83数据分析：从实验结果可以看出，摆动角度越大，摆动周期越长。

这与我们的预期相符，因为从理论上来说，摆角越大，重力的影响就越大，所以摆动的周期会变长。

结论：通过本次实验，我们验证了单摆的运动规律：摆动周期与摆长有关，与摆锤质量和初摆角度无关。

因此，单摆可以用来研究重力的作用和简谐振动的规律。

实验结果与理论模型相吻合，验证了单摆的运动特性。

讨论和改进：在实验中，我们假设了摆锤质量和初摆角度对摆动周期没有影响。

但实际上，摆锤质量和初摆角度都会对摆动周期产生一定影响。

进一步研究可以考虑加入这些因素，并通过更多的实验数据进行分析和比较。

结尾：本实验通过研究单摆的运动规律，加深了我们对重力和简谐振动的理解。

单摆运动规律的研究资料单摆运动是物理学中的一个重要领域，它涉及了波动理论和力学原理。

单摆的运动规律不仅在科学研究中有着广泛的应用价值，而且在我们日常生活中也有着非常重要的实践意义。

下面就是单摆运动规律的一些研究资料。

一、单摆的定义单摆是由一个质量为m的物体（摆球）悬挂在一根长度为L的细线上所组成的系统。

在重力作用下，摆球能够沿着一条弧线运动，并在此过程中不断地转换着其重力势能和动能。

因此，单摆是一个典型的能量守恒系统。

1. 单摆的周期单摆的周期是指摆球从一个方向摆到另一个方向所需的时间。

当摆角小于10°时，单摆的周期可以用如下公式计算：T = 2π(L/g) ½其中T为周期，L为摆绳的长度，g为重力加速度。

2. 单摆的运动方程单摆的运动方程可以表示为如下形式：θ'' + (g/L)sinθ = 0其中θ为摆球的摆角，θ''为摆球的加速度。

为了求解摆球的运动方程，可以采用分离变量法，设θ(t) = Asin(ωt + φ)，其中A为振幅，ω为角频率，φ为初相位，代入上述方程即可。

3. 单摆的能量守恒单摆可以看作是一个完整的能量守恒系统，在其运动过程中，能量的总和始终保持不变。

当摆球处于最高点时，它的动能最小，而重力势能最大；当摆球处于最低点时，它的动能最大，而重力势能最小。

因此，在单摆运动的任意时刻，其重力势能和动能之和始终等于系统的总能量。

三、单摆运动的应用1. 单摆用于测量地球重力加速度利用单摆可以测量地球的重力加速度，因为单摆摆动的周期与地球的重力加速度和摆长有关。

在实际应用中，可以通过不断地调整摆长，从而测定地球的重力加速度。

2. 单摆用于测量时间在古代，人们常常利用单摆来测量时间。

因为单摆的周期相对稳定，而且可以进行精确的调整，因此在没有显微镜的时代，单摆是一种非常实用的测时仪器。

3. 单摆用于研究摆动系统单摆是一个具有理论性的简谐运动系统，因此在科学研究中有着广泛的应用。

单摆运动研究报告1. 引言单摆是一种简单而又经典的物理学实验，研究其运动规律对于理解力学基本原理具有重要意义。

在本研究报告中，我们将通过实验和数值模拟的方法，探究单摆运动的特点和变化规律。

2. 实验方法2.1 实验设备我们使用了以下实验设备： - 支架：用于支撑单摆装置的结构。

- 钢丝：作为单摆的支撑杆。

- 质量球：作为单摆的挂摆物。

- 计时器：用于测量单摆的周期。

2.2 实验步骤1.将支架安装在水平台面上，并将钢丝悬挂在支架上。

2.调整钢丝的长度，使得质量球可以在自由摆动的状态下。

3.启动计时器，测量质量球摆动的周期。

4.重复实验步骤3，至少进行5次测量，取平均值作为结果。

3. 实验结果分析3.1 实验数据根据实验步骤中记录的数据，我们得到了以下单摆摆动周期的测量结果：实验次数摆动周期 (s)1 1.232 1.193 1.254 1.215 1.243.2 摆动周期与摆长的关系为了研究摆动周期与摆长的关系，我们进行了一系列的实验，并绘制了如下的图表：周期与摆长的关系周期与摆长的关系由图表可知，摆动周期与摆长呈正比关系。

摆长增加时，周期增加；摆长减小时，周期减小。

3.3 摆动周期与重力加速度的关系为了研究摆动周期与重力加速度的关系，我们进行了一系列的实验，并绘制了如下的图表：周期与重力加速度的关系周期与重力加速度的关系由图表可知，摆动周期与重力加速度呈平方根关系。

重力加速度增加时，周期减小；重力加速度减小时，周期增加。

4. 数值模拟除了实验研究外，我们还进行了数值模拟，以验证实验结果。

通过使用物理引擎模拟单摆的运动，我们得到了以下结果：•摆动周期与摆长的关系：数值模拟结果与实验结果一致，均验证了摆动周期与摆长呈正比关系。

•摆动周期与重力加速度的关系：数值模拟结果与实验结果一致，均验证了摆动周期与重力加速度呈平方根关系。

5. 结论通过实验和数值模拟的方法，我们得出了以下结论： 1. 单摆的摆动周期与摆长呈正比关系。

实验题目：单摆的设计和研究实验目的：利用经典的单摆公式、给出的器材和对重力加速度g的测量精度的要求，进行简单的设计性实验基本方法的训练，学会应用误差均分原理选用适当的仪器和测量方法，学习积累放大法的原理及应用，分析误差的来源，提出进行修正和估算的方法。

实验器材：提供的器材及参数：游标卡尺、米尺、千分尺、电子秒表、支架、细线、钢球、摆幅测量标尺、天平摆长l≈70.00cm，摆球直径D≈2.00cm，摆动周期T≈1.700s，米尺精度Δ米≈0.05cm，卡尺精度Δ卡≈0.002cm，千分尺精度Δ千≈0.001cm，秒表精度Δ秒≈0.01s，人开、停秒表总反应时间Δ人≈0.2s实验原理：在本实验中，实验精度Δg/g<1%，故摆球的几何形状、摆的质量、空气浮力、摆角等因素对测量造成的修正项均是高阶小量，可忽略。

那么近似的周期测量公式为，故可通过误差均分原理，在一定的精度范围内测量T、L，从而求得重力加速度g。

实验设计：由，得：。

两边取对数处理，有：Δg/g=2ΔT/T+ΔL/L。

若要求Δg/g<1%，由误差均分原理，就应该有2ΔT/t<0.5%且ΔL/L<0.5%，其中t=nT，n=1、2、……，L=l+D/2，l表示摆线长，D表示摆球直径，ΔT=Δ秒+Δ人≈0.01s+0.2s=0.21s。

那么ΔL<0.5%≈0.5%(70.00cm+2.00cm/2)=0.335cm，故选用米尺测量摆线长，用游标卡尺测量摆球的直径，ΔL可满足条件。

由于t>ΔT/0.5%≈84s，即nT>84s，将T≈1.700s代入，知一次测量若需达到要求的精度，需测量n=50(nT≈85s>84s)个周期的时间。

除上述分析中提到的实验仪器外，还需要选择电子秒表、支架、细线、钢球。

实验步骤：1、按照实验要求组装好实验仪器，将电子秒表归零；2、多次（3-5次，本实验中5次）测量摆球直径、摆线长度；3、将摆球拉离平衡位置使其小角度（小于5度）同平面摆动；4、多次（3-5次，本实验中5次）用电子秒表测量单摆50次全振动所需时间；5、整理仪器；6、数据处理和误差分析。

单摆运动规律的研究报告摘要：本研究旨在研究单摆运动的规律及其数学描述。

通过在实验中测量单摆的周期、摆动幅度和摆动角度，并采用数学模型进行分析，得出了单摆运动的规律，并与理论值进行对比。

实验结果表明，单摆运动的周期与摆长的平方根成正比，而与摆动角度无关，从而验证了单摆运动规律的数学描述。

这一研究对于深入理解单摆的运动特性及其在物理学研究和实际应用中的意义具有重要的作用。

关键词：单摆；运动规律；周期；摆动幅度；摆动角度引言：单摆是物理学中经典力学的重要实验装置之一，广泛应用于物理实验和教学中。

对于单摆运动的规律及其数学描述的研究，不仅可以深入理解单摆的特性，还可以更好地应用于物理学研究和实际应用中。

本研究旨在通过实验测量和数学模型分析，研究单摆运动的规律及其数学描述，以期能为相关领域的深入研究提供参考和依据。

实验方法：1.准备工作：利用线和线组装一个具有一定摆长的单摆；利用测量工具测量单摆的摆长。

2.实验测量：调整单摆的摆长和摆动角度，并启动单摆的运动，使用计时器测量单摆的摆动时间、周期和摆动角度。

3.数据记录：将实验测量得到的数据记录下来，包括单摆的摆长、摆动时间、周期和摆动角度。

4.数据处理：根据实验测量数据计算平均周期、变化的摆动角度和摆动幅度。

5.数学模型：利用已有的单摆数学模型进行分析和计算，得出单摆运动的规律。

实验结果及讨论：1.实验测量结果：根据实验测量数据，计算得出单摆的平均周期和摆动幅度。

2.展示数据：将实验测量和计算结果绘制成折线图，以直观展示单摆运动的规律。

3.数学模型分析：使用已有的单摆数学模型，根据摆长和摆动角度计算单摆的周期。

4.结果对比：将实验测量结果与理论值进行对比，以验证单摆运动规律的数学描述的准确性。

结论：通过实验测量和数学模型分析，本研究得出了单摆运动规律的数学描述，即单摆的周期与摆长的平方根成正比，而与摆动角度无关。

实验结果与理论值的对比表明，单摆运动规律的数学描述是准确和可靠的。

单摆运动规律的研究摘要单摆问题是高中物理及大学普通物理实验教学中的一个根底问题。

受各种因素的影响，其运动规律较为复杂。

本文建立了理想模式下单摆的数学模型，现实情况下单摆的数学模型.等对单摆的运动进展了探究。

首先，本文从理想情况出发，由牛顿第二定律进展推理，建立了无阻尼小角度单摆运动模型，对单摆的运动进展了初步探究。

然后，本文又建立了无阻尼大角度单摆运动模型，进一步完善了理想模式下单摆的数学模型。

最后，本文从实际出发，考虑单摆运动中受到的阻力因素，以理想模式下单摆的数学模型为根底，建立了现实情况下单摆的运动模型，深度的对单摆运动进展了探索。

关键词简谐运动角度阻尼运动单摆运动目录一、问题的描述二、模型假设三、模型建立及求解1 理想模式下单摆的数学模型1.1 小角度单摆运动模型1.1.1 模型建立1.1.2 模型求解1.1.3 结果分析1.2 大角度单摆运动模型1.2.1 模型建立1.2.2 模型求解1.2.3 结果分析2 现实模式下单摆的数学模型2.1 小、大阻尼单摆运动模型2.1.1 模型建立2.1.2 模型求解2.1.3 结果分析四模型分析一问题的描述根据平常接触到的摆钟、秋千等实物中，我们可以抽象出单摆的模型。

细线一端固定在悬点,另一端系一个小球,如果细线的质量与小球相比可以忽略,球的直接与线的长度相比也可以忽略,这样的装置就叫做单摆.我们从理想情况出发进展分析，并逐渐完善从而推导出单摆实际运动规律。

二模型假设1悬挂小球的细线伸缩和质量均忽略不记，线长比小球的直径大得多；2.装置严格水平；3.无驱动力。

三模型建立及求解1 理想模式下单摆的数学模型图1简单单摆模型在t时刻，摆锤所受切向力ft(t)是重力mg在其运动圆弧切线方向上的分力，即f(t) =mg sin(t)完全理想条件下，根据牛顿第二运动定律，切向加速度为：a(t)=gsin(t)因此得到单摆的运动微分方程组：1.1 小角度单摆运动模型1.1.1模型建立当摆角θ很小时,sinθ≈θ，故方程1可简化为:1.1.2 模型求解利用matlab软件在[0, 5o]分别作出方程〔1〕和方程〔2〕的解得图像小角度单摆摆动规律〔—方程〔1〕的解，**方程〔2〕的解〕1.1.3 结果分析由图像可以看出两方程的解的图像几乎吻合，可以说明当较小时〔θ<5〕，两方程的解几乎相等，单摆运动可看为简谐运动。

一、实验目的1. 研究单摆的周期特性与摆长、摆角、摆球质量等因素的关系。

2. 验证单摆运动遵循简谐运动规律。

3. 测量并计算当地的重力加速度。

二、实验原理单摆是一种经典的物理模型，其运动规律遵循简谐运动。

当摆角θ较小（通常小于5°）时，单摆的运动可以近似为简谐运动。

单摆的周期T与摆长L和重力加速度g的关系为：\[ T = 2\pi \sqrt{\frac{L}{g}} \]其中，T为单摆的周期，L为摆长，g为重力加速度。

三、实验仪器1. 单摆装置（包括细线、摆球、固定装置等）2. 秒表（用于测量周期）3. 游标卡尺（用于测量摆球直径）4. 米尺（用于测量摆长）5. 计算器四、实验步骤1. 测量摆长L：使用米尺测量摆线的长度，并记录下来。

2. 测量摆球直径d：使用游标卡尺测量摆球的直径，并记录下来。

3. 测量周期T：a. 将摆球拉至一定角度（确保摆角小于5°），然后释放。

b. 使用秒表测量摆球完成n次全振动所需的时间，记录下来。

c. 计算单次全振动的周期T = 时间/n。

4. 重复步骤3，至少测量5次，以减小误差。

五、数据处理1. 将测量得到的摆长L、摆球直径d、周期T等数据记录在表格中。

2. 根据公式 \( T = 2\pi \sqrt{\frac{L}{g}} \) 计算重力加速度g。

3. 计算重力加速度g的平均值和标准偏差。

六、实验结果与分析1. 摆长L与周期T的关系：通过实验数据可以发现，随着摆长L的增加，周期T也随之增加，且二者呈线性关系。

这与理论公式 \( T = 2\pi \sqrt{\frac{L}{g}} \) 相符。

2. 摆角θ与周期T的关系：当摆角θ较小时（小于5°），周期T基本保持不变。

但当摆角θ较大时，周期T会明显增加，说明摆角θ对周期T有显著影响。

3. 摆球质量m与周期T的关系：实验结果表明，摆球质量m对周期T的影响较小，可以忽略不计。

4. 重力加速度g的测量：根据实验数据计算得到的重力加速度g的平均值与理论值基本一致，说明实验结果可靠。

单摆的研究一．实验目的：1。

研究单摆振动的周期与摆长的关系；2。

学习光电计时的使用方法；3。

用单摆测量重力加速度g 。

二．实验器材：单摆装置，光电计时器，钢卷尺，卡尺。

三．实验原理：单摆是由一根不能伸长的轻质细线和悬在此线下端体积很小的重球所构成。

在摆长远大于球的直径，摆球质量远大于线的质量的条件下，单摆在摆角很小（<θ5°）时，在平衡位置左右作周期性的往返摆动，可近似为简谐振动。

其振动周期为： T=2πg L由此得： 224T Lg π=实验中只需量出摆长，测定摆动的周期，就可计算出g 值。

四．实验内容及步骤： 1．悬挂单摆：使摆长为1m 左右，装好摆球，调节底座上的水平调节螺丝，使摆线与立柱平行。

2．测量摆长L ：测量摆线悬点与摆球质心之间的距离L 。

由于摆球质心位置难找，可用米尺测悬点到摆球的距离L 1，用千分尺（或卡尺）测球的直径d ，（各测三次求平均值），则摆长： L=L 1+d/2。

3．测定摆动的周期T ：使摆角约为4°，测量摆球往返摆动50次所需时间t 50，重复测量3次，求出平均值：T=50350⨯∑t。

测量时，选择摆球通过最低点时开始计时，按表时数“0”，以后每完成一个周期数1，2，3，…，最后计算时单位统一为秒。

4.将所测数据列于下表中，并计算出摆长、周期及重力加速度g （由224TL g π=计算）。

对式 g=4π2212/T d L +根据不确定度的相对式P 12有：2222221)ln ()ln ()ln (1T d l g U Tg U dg U l g g U ∂∂+∂∂+∂∂= 其中，Ln g=Ln 24π+Ln (L 1+d/2)－Ln T 21ln l g ∂∂=L d L 12/11=+ Ld L d g 212/21ln 1=+=∂∂ T T g 2ln -=∂∂直测量不确定度U L1 ≈ U LB =仪∆/3=钢卷尺最小刻度/2÷3=0.5㎜÷3=0.29㎜=0.029㎝。