中考数学总复习:相交弦定理切割线定理
- 格式:ppt
- 大小:130.00 KB
- 文档页数:46
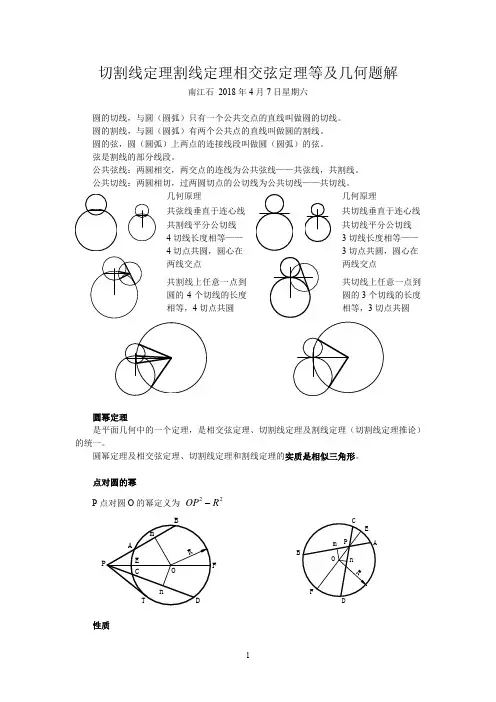
切割线定理割线定理相交弦定理等及几何题解南江石 2018年4月7日星期六圆的切线,与圆(圆弧)只有一个公共交点的直线叫做圆的切线。
圆的割线,与圆(圆弧)有两个公共点的直线叫做圆的割线。
圆的弦,圆(圆弧)上两点的连接线段叫做圆(圆弧)的弦。
弦是割线的部分线段。
公共弦线:两圆相交,两交点的连线为公共弦线——共弦线,共割线。
公共切线:两圆相切,过两圆切点的公切线为公共切线——共切线。
几何原理 几何原理共弦线垂直于连心线共切线垂直于连心线共割线平分公切线 共切线平分公切线4切线长度相等—— 4切点共圆,圆心在两线交点3切线长度相等——3切点共圆,圆心在两线交点共割线上任意一点到圆的4个切线的长度相等,4切点共圆共切线上任意一点到圆的3个切线的长度相等,3切点共圆圆幂定理是平面几何中的一个定理,是相交弦定理、切割线定理及割线定理(切割线定理推论)的统一。
圆幂定理及相交弦定理、切割线定理和割线定理的实质是相似三角形。
点对圆的幂P 点对圆O 的幂定义为22R OP FB性质点P 对圆O 的幂的值,和点P 与圆O 的位置关系有下述关系: 点P 在圆O 内→P 对圆O 的幂为负数; 点P 在圆O 外→P 对圆O 的幂为正数; 点P 在圆O 上→P 对圆O 的幂为0。
切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
PBPTPT PA =PB PA PT ∙=2 222Am Pm PT -=割线定理(切割线定理的推论)从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
PD PC PB PA ∙=∙2222Cn Pn Am Pm -=-相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等,或经过圆内一点引两条弦,各弦被这点所分成的两线段的积相等。
PD PC PB PA ∙=∙2222A Pn Cn Pm m -=-垂径定理(相交弦定理推论)如果弦与直径垂直相交,那么弦的一半是它所分直径所成的两条线段的比例中项。

初中切割线定理
切割线定理是初中数学中的一种几何定理,主要用于解决与三角形有关的问题。
它的表述如下:若一直线割一三角形之两边(或延长线)而交其他两边(或其延长线)于两点,则此直线截得的三角形面积等于被割去的两部分面积和的一半。
例如,在一个三角形ABC中,如果有一条直线DE从A点出发,经过BC边上的点D,然后到达AC边上的点E,那么根据切割线定理,我们就可以得出:三角形ADE的面积等于三角形ABD的面积加上三角形ACE的面积的一半。
这个定理在解题中非常有用,可以帮助我们快速计算出一些难以直接测量的面积,或者用来证明两个三角形的面积相等。
在学习和应用切割线定理时,我们需要理解其背后的逻辑,并熟练掌握相关的几何知识。
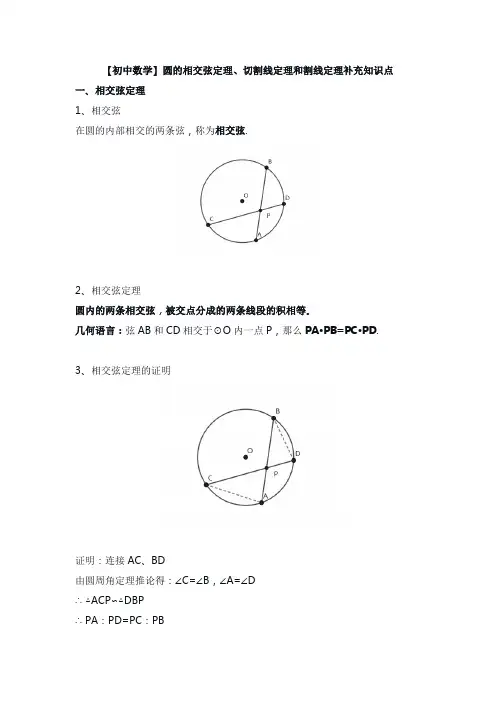
【初中数学】圆的相交弦定理、切割线定理和割线定理补充知识点一、相交弦定理1、相交弦在圆的内部相交的两条弦,称为相交弦.2、相交弦定理圆内的两条相交弦,被交点分成的两条线段的积相等。
几何语言:弦AB和CD相交于⊙O内一点P,那么PA·PB=PC·PD. 3、相交弦定理的证明证明:连接AC、BD由圆周角定理推论得:∠C=∠B,∠A=∠D∴△ACP∽△DBP∴ PA:PD=PC:PB二、切割线定理1、切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
几何语言:BC是⊙O的一条割线,PA是⊙O的一条切线,切点为A,则:PA²=PB·PC。
2、切割线定理的证明证明:如图,连接AB,AC∵ PA是圆O的切线,由弦切角定理可得∴∠PAC=∠B∵∠APB=∠CPA∴△APC∽△BPA∴ PA:BP=PC:PA三、割线定理1、割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
几何语言:从⊙O一点P引圆的两条割线AB、CD,则:PA·PB=PC·PD.2、割线定理证明证明:如图,连接AD、BC,由圆周角定理推论,得:∠D=∠B∵∠BPC=∠DPA∴△BPC∽△DPA∴ PB:PD=PC:PA∴ PA·PB=PC·PD四、例题例1、如图,在⊙O中,弦AB=CD,AB⊥CD于点E,已知CE·ED=3,BE =1,求⊙O的直径。
解:作OH⊥AB于H,OG⊥CD于G,连接OA由相交弦定理得:CE·ED=AE·EB∴ 3=AE×1∴ AE=3∴ AB=AE+EB=3+1=4∴ AB=CD=4∴ AH=HB=2∴ HE=HB-EB=2-1=1∵ AB=CD,AB⊥CD∴ OH=OG∴四边形OGEH为正方形∴ OH=HE=1由勾股定理得,OA=,∴⊙O的直径为,例2、如题图,⊙O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3, CE:ED=2:1 ,求BE的值。

第二十二讲园幂定理相交弦定理、切割线定理、割线定理统称为圆幂定理.圆幂定理实质上是反映两条相交直线与圆的位置关系的性质定理,其本质是与比例线段有关.相交弦定理、切割线定理、割线定理有着密切的联系,主要体现在:1.用运动的观点看,切割线定理、割线定理是相交弦定理另一种情形,即移动圆内两条相交弦使其交点在圆外的情况;2.从定理的证明方法看,都是由一对相似三角形得到的等积式.熟悉以下基本图形、基本结论:【例题求解】【例1】如图,PT切⊙O于点T,PA交⊙O于A、B两点,且与直径CT交于点D,CD=2,AD=3,BD=6,则PB= .思路点拨综合运用圆幂定理、勾股定理求PB长.注:比例线段是几何之中一个重要问题,比例线段的学习是一个由一般到特殊、不断深化的过程,大致经历了四个阶段:(1)平行线分线段对应成比例;(2)相似三角形对应边成比例;(3)直角三角形中的比例线段可以用积的形式简捷地表示出;(4)圆中的比例线段通过圆幂定理明快地反映出.【例2】 如图,在平行四边形ABCD 中,过A 、B 、C 三点的圆交AD 于点E ,且与CD 相切,若AB=4,BE=5,则DE 的长为( ) A .3 B .4 C .415 D .516思路点拨 连AC ,CE ,由条件可得许多等线段,为切割线定理的运用创设条件.注:圆中线段的算,常常需要综合相似三角形、直角三角形、圆幂定理等知识,通过代数化获解,加强对图形的分解,注重信息的重组与整合是解圆中线段计算问题的关键.【例3】 如图,△ABC 内接于⊙O ,AB 是∠O 的直径,PA 是过A 点的直线,∠PAC=∠B .(1)求证:PA 是⊙O 的切线;(2)如果弦CD 交AB 于E ,CD 的延长线交PA 于F ,AC=8,CE :ED=6:5,,AE :BE=2:3,求AB 的长和∠ECB 的正切值.思路点拨 直径、切线对应着与圆相关的丰富知识.(1)问的证明为切割线定理的运用创造了条件;引入参数x 、k 处理(2)问中的比例式,把相应线段用是的代数式表示,并寻找x与k 的关系,建立x 或k 的方程.【例4】如图,P是平行四边形AB的边AB的延长线上一点,DP与AC、BC分别交于点E、E,EG是过B、F、P三点圆的切线,G为切点,求证:EG=DE思路点拨由切割线定理得EG2=EF·EP,要证明EG=DE,只需证明DE2=EF·EP,这样通过圆幂定理把线段相等问题的证明转化为线段等积式的证明.注:圆中的许多问题,若图形中有适用圆幂定理的条件,则能化解问题的难度,而圆中线段等积式是转化问题的桥梁.需要注意的是,圆幂定理的运用不仅局限于计算及比例线段的证明,可拓展到平面几何各种类型的问题中.【例5】如图,以正方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF 切半圆于点E,交AB的延长线于点F,BF=4.求:(1)cos∠F的值;(2)BE的长.思路点拨解决本例的基础是:熟悉圆中常用辅助线的添法(连OE,AE);熟悉圆中重要性质定理及角与线段的转化方法.对于(1),先求出EF,FO值;对于(2),从△BE F∽△EAF,Rt△AEB入手.注:当直线形与圆结合时就产生错综复杂的图形,善于分析图形是解与圆相关综合题的关键,分析图形可从以下方面入手:(1)多视点观察图形.如本例从D点看可用切线长定理,从F点看可用切割线定理.(2)多元素分析图形.图中有没有特殊点、特殊线、特殊三角形、特殊四边形、全等三角形、相似三角形.(3)将以上分析组合,寻找联系.学力训练1.如图,PT是⊙O的切线,T为切点,PB是⊙O的割线,交⊙O于A、B两点,交弦CD于点M,已知CM=10,MD=2,PA=MB=4,则PT的长为.2.如图,PAB、PCD为⊙O的两条割线,若PA=5,AB=7,CD=11,则AC:BD= .3.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点F,若AB=CD=2,则CE= .4.如图,在△ABC中,∠C=90°,AB=10,AC=6,以AC为直径作圆与斜边交于点P,则BP的长为( )A.6.4 B.3.2 C .3.6 D.85.如图,⊙O 的弦AB 平分半径OC ,交OC 于P 点,已知PA 、PB 的长分别为方程024122=+-x x 的两根,则此圆的直径为( )A .28B .26C .24D .226.如图,⊙O 的直径Ab 垂直于弦CD ,垂足为H ,点P 是AC 上一点(点P 不与A 、C 两点重合),连结PC 、PD 、PA 、AD ,点E 在AP 的延长线上,PD 与AB 交于点F ,给出下列四个结论:①CH 2=AH ·BH ;②AD =AC :③AD 2=DF ·DP ;④∠EPC=∠APD ,其中正确的个数是( )A .1B .2C .3D .47.如图,BC 是半圆的直径,O 为圆心,P 是BC 延长线上一点,PA 切半圆于点A ,AD ⊥BC 于点D .(1)若∠B=30°,问AB 与AP 是否相等?请说明理由; (2)求证:PD ·PO=PC ·PB ;(3)若BD :DC=4:l ,且BC =10,求PC 的长.8.如图,已知PA 切⊙O 于点A ,割线PBC 交⊙O 于点B 、C ,PD ⊥AB 于点D ,PD 、AO 的延长线相交于点E ,连CE 并延长交⊙O 于点F ,连AF . (1)求证:△PBD ∽△PEC ; (2)若AB=12,tan ∠EAF=32,求⊙O 的半径的长.9.如图,已知AB 是⊙O 的直径,PB 切⊙O 于点B ,PA 交⊙O 于点C ,PF 分别交AB 、BC 于E 、D ,交⊙O 于F 、G ,且BE 、BD 恰哈好是关于x 的方程0)134(622=+++-m m x x⌒⌒⌒(其中m 为实数)的两根.(1)求证:BE=BD ;(2)若GE ·EF=36,求∠A 的度数.10.如图,△ABC 中,∠C=90°,O 为AB 上一点,以O 为圆心,OB 为半径的圆与AB 相交于点E ,与AC 相切于点D ,已知AD=2,AE=1,那么BC= .11.如图,已知A 、B 、C 、D 在同一个圆上,BC=CD ,AC 与BD 交于E ,若AC=8,CD=4,且线段BE 、ED 为正整数,则BD= .12.如图,P 是半圆O 的直径BC 延长线上一点,PA 切半圆于点A ,AH ⊥BC 于H ,若PA=1,PB+PC=a (a >2),则PH=( )A .a 2 B .a 1 C .2a D .3a13.如图,△ABC 是⊙O 的内接正三角形,弦EF 经过BC 的中点D ,且EF ∥AB ,若AB=2,则DE 的长为( )A .21 B .215 C .23D .1 14.如图,已知AB 为⊙O 的直径,C 为⊙O 上一点,延长BC 至D ,使CD=BC ,CE ⊥AD 于E ,BE 交⊙O 于F ,AF 交CE 于P ,求证:PE=PC .15.已知:如图,ABCD 为正方形,以D 点为圆心,AD 为半径的圆弧与以BC 为直径的⊙O 相交于P 、C 两点,连结AC 、AP 、CP ,并延长CP 、AP 分别交AB 、BC 、⊙O 于E 、H 、F 三点,连结OF .(1)求证:△AEP ∽△CEA ;(2)判断线段AB 与OF 的位置关系,并证明你的结论; (3)求BHHC16.如图,PA 、PB 是⊙O 的两条切线,PEC 是一条割线,D 是AB 与PC 的交点,若PE=2,CD=1,求DE 的长.17.如图,⊙O 的直径的长是关于x 的二次方程0)2(22=+-+k x k x (k 是整数)的最大整数根,P 是⊙O 外一点,过点P 作⊙O 的切线PA 和割线PBC ,其中A 为切点,点B 、C 是直线PBC 与⊙O 的交点,若PA 、PB 、PC 的长都是正整数,且PB 的长不是合数,求PA+PB+PC 的值.参考答案。

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段学习目标1.切线长概念切线长是在经过圆外一点的圆的切线上;这点和切点之间的线段的长度;“切线长”是切线上一条线段的长;具有数量的特征;而“切线”是一条直线;它不可以度量长度..2.切线长定理对于切线长定理;应明确1若已知圆的两条切线相交;则切线长相等;2若已知两条切线平行;则圆上两个切点的连线为直径;3经过圆外一点引圆的两条切线;连结两个切点可得到一个等腰三角形;4经过圆外一点引圆的两条切线;切线的夹角与过切点的两个半径的夹角互补;5圆外一点与圆心的连线;平分过这点向圆引的两条切线所夹的角..3.弦切角:顶点在圆上;一边和圆相交;另一边和圆相切的角..直线AB切⊙O于P;PC、PD为弦;图中几个弦切角呢四个4.弦切角定理:弦切角等于其所夹的弧所对的圆周角..5.弄清和圆有关的角:圆周角;圆心角;弦切角;圆内角;圆外角..6.遇到圆的切线;可联想“角”弦切角;“线”切线的性质定理及切线长定理..7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中;AB、CD为弦;交于P.PA·PB=PC·PD.连结AC、BD;证:△APC∽△DPB.相交弦定理的推论⊙O中;AB为直径;CD⊥AB于P.PC2=PA·PB.用相交弦定理.切割线定理⊙O中;PT切⊙O于T;割线PB交⊙O于APT2=PA·PB连结TA、TB;证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线;交⊙O于A、CPA·PB=PC·PD过P作PT切⊙O于T;用两次切割线定理圆幂定理⊙O中;割线PB交⊙O于A;CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M;延长OP'交⊙O于N;用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线;交⊙O于两点;则自定点P到两交点的两条线段之积为常数||R为圆半径;因为叫做点对于⊙O的幂;所以将上述定理统称为圆幂定理..。


九年级数学相交弦定理和切割线定理知识精讲一. 本周教学内容:相交弦定理和切割线定理二. 重点、难点:1. 相交弦定理的使用特征。
2. 切割线定理的使用特征。
[例1] 如图,AC=BD ,CE 、DF 切⊙O 于E 、F 两点,连EF ,求证:CM=MD 。
证明:作DN ∥EC ,交MF 于N ,那么∠1=∠2,∠C=∠4 由弦切角定理得:∠3=∠1 ∴ ∠2=∠3 ∴ DN=DF由切割线定理,CB CA CE ⋅=2DA DB DF ⋅=2∵ AC=DB ∴ CB=DA ∴ 22DF CE = CE=DF∴ CE=DN 又 ∵ ∠5=∠6 ∴ DNM CEM ∆≅∆〔AAS 〕 ∴ CM=MD[例2] PT 切⊙O 于T ,PBA 为割线,交OC 于D ,CT 为直径,假设OC=BD=4cm ,AD=3cm ,求PB 长。
解:设即3由切割线定理,BP AP PT ⋅=2 由勾股定理,222TD PT PD +=∴ 22TD BP AP PD +⋅= ∴ )7(6)4(22++=+y y y∴ cm y 20=[例3]假设BC=9,解:连AB ,∴ ∠1=∴EF CE =由相交弦定理得26⨯=ab ② 由①、②解得:4=b ,3=a 由切割线定理得:1441692=⨯=⋅=CF CB AC ∴ AC=12[例4] P 为弦AB 上一点,C 在圆O 上,OP ⊥PC ,求证:〔1〕PB PA PC ⋅=2〔2〕假设证明:〔1〕延长CP 解:〔2〕易知PM 由相交弦定理,MN CM MB AM ⋅=⋅,即27)63(3)3(=+⨯=+y x ① 由垂径定理,CP=PD ,故在CPO Rt ∆中有2046222=-=PC ∴ 由〔1〕结论,20)3(=+y x ② 由①—②得:37+=x y 代②得,0203162=-+x x ∴ 0601632=-+x x ,36128±-=x 〔舍负〕∴ AP 长为36128+-[例5] 如图,AB 切⊙O 于B ,OB 交割线ACD 于E ,AC=CE=3,OE=25,求AB 长。

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段1.切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
2弦切角定理及其推论圆周角∠CAB,让射线AC绕点A旋转,产生无数个圆周角,当AC绕点A旋转至与圆相切时,停止旋转,得∠BAE问:这时∠BAE还是圆周角吗?为什么?像∠BAE这样的角叫做弦切角,请你仿照圆周角的定义,给出弦切角的定义:_____________________________________________________________________________________________问题:以下各图中的角哪个是弦切角?思考:弦切角相对于圆心的位置,分为哪几类?请在右上方画出图。
问题:已知如图,AB是⊙O的一条切线,A为切点,AC是⊙O的一条弦,则∠ADC与∠BAC有什么关系?请给出证明。
(提示:类比圆周角定理的证明方法)弦切角定理:________________________________________________________问题:若两个弦切角所夹的弧相等,,那么这两个弦切角相等吗?为什么?弦切角定理的推论:___________________________________________________例如图,AD是ΔABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB,AC分别相交于E,F. 求证:EF∥BC.一、选择题(共17小题)1、如图,BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点.若∠ADE=19°,则∠AFB的度数为何?()A、97°B、104°C、116°D、142°2、如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则的度数为何()A、50°B、60°C、100°D、120°3、如图,CD是⊙O的切线,T为切点,A是上的一点,若∠TAB=100°,则∠BTD的度数为()A、20°B、40°C、60°D、80°4、如图,四边形ABCD内接于⊙O,AB=BC.AT是⊙O的切线,∠BAT=55°,则∠D等于()A、110°B、115°C、120°D、125°5、如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于()A、30°B、60°C、90°D、120°6、如图,△ABC是⊙O的内接三角形,AD是⊙O的切线,点A为切点,∠ACB=60°,则∠DAB的度数是()A、30°B、45°C、60°D、120°7、已知:如图,E是相交两圆⊙M和⊙N的一个交点,且ME⊥NE,AB为外公切线,切点分别为A,B连接AE,BE,则∠AEB的度数为()8、如图,直线AB切⊙O于点A,割线BDC交⊙O于点D、C.若∠C=30°,∠B=20°,则∠ADC=()A、70°B、50°C、30°D、20°9、如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于()度.A、40B、50C、70D、8010、如图,P为半⊙O直径BA延长线上一点,PC切半⊙O于C,且PA:PC=2:3,则sin∠ACP的值为_______11、如图AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为( )A、30°B、40°C、50°D、60°12、如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于()A、40°B、50°C、60°D、70°13、如图,AB、CD是⊙O的两条平行弦,BE∥AC交CD于E,过A点的切线交DC延长线于P,若AC=则PC•CE的值是()A、18B、6C、D、14、如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN互余的角有()A、1个B、2个C、3个D、4个则∠ACB等于()A、70°B、55°C、70°或110°D、55°或125°16、如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是()A、50°B、55°C、60°D、65°17、如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是()A、30°B、45°C、50°D、60°二、填空题(共13小题)18、如图,已知AD为⊙O的切线,⊙O的直径是AB=2,弦AC=1,则∠CAD=_________度.19、已知⊙O 中,的度数为70°,过点A的直线AC与⊙O相切,则弦切角∠BAC的度数为_________.20、如图,AB切⊙O于C,AO交⊙O于D,AO的延长线交⊙O于E,若∠A=α,则∠ECB=_________(用含α的式子表示).21、如图,△ABC内接于圆⊙O,CT切⊙O于C,∠ABC=100°,∠BCT=40°,则∠AOB=___度.22、如图,割线PAB过圆心O,PD切⊙O于D,C 是上一点,∠PDA=20°,则∠C的度数是______度.23、如图,PA、PB是⊙O的两条切线,A、B为切点,则∠ABO ﹣∠ABP=___.24、如图,四边形ABED内接于⊙O,E是AD延长线上的一点,若∠AOC=122°,则∠B=_________度,25、如图,已知AB是⊙O的弦,AC切⊙O于点A,∠BAC=60°,则∠ADB的度数为_________度.26、如图,AB为⊙O直径,CE切⊙O于点C,CD⊥AB,D为垂足,AB=12cm,∠B=30°,则∠ECB=_________度;CD=_________cm.27、如图,已知AB是圆O的弦,AC是圆O的切线,∠BAC的平分线交圆O于D,连BD并延长交AC于点C,若∠DAC=40°,则∠B=_________度,∠ADC=_________度.28、如图,PA切⊙O于A点,C是弧AB上任意一点,∠PAB=58°,则∠C的度数是_________度.29、如图,EF切△ABC的外接圆于C,∠BAC=80°,那么∠BCE=_________度.30、已知:如图,在⊙O中,AB是直径,四边形ABCD内接于⊙O,∠BCD=130°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为_________.3.与圆有关的比例线段 定理 图形 已知 结论 证法相交弦 定理⊙O 中,AB 、CD 为弦,交于P. PA·PB=PC·PD . 连结AC 、BD ,证:△APC∽△DPB .相交弦定理的推论⊙O 中,AB 为直径,CD⊥AB 于P.PC 2=PA·PB . 用相交弦定理.切割线 定理⊙O 中,PT 切⊙O 于T ,割线PB 交⊙O 于APT 2=PA·PB 连结TA 、TB ,证:△PTB∽△PAT切割线 定理推论PB 、PD 为⊙O 的两条割线,交⊙O 于A 、CPA·PB=PC·PD 过P 作PT 切⊙O 于T ,用两次切割线定理圆幂定理⊙O 中,割线PB 交⊙O 于A ,CD 为弦 P'C·P'D=r 2-OP'2PA·PB=OP 2-r 2r 为⊙O 的半径延长P'O 交⊙O 于M ,延长OP'交⊙O 于N ,用相交弦定理证;过P 作切线用切割线定理勾股定理证8.圆幂定理:过一定点P 向⊙O 作任一直线,交⊙O 于两点,则自定点P 到两交点的两条线段之积为常数||(R 为圆半径),因为叫做点对于⊙O 的幂,所以将上述定理统称为圆幂定理。

初三数学相交弦定理和切割线定理一. 本周教学内容:相交弦定理和切割线定理二. 重点、难点:1.[例yBP=,则y关于x的函数关系式为。
解:由相交弦定理得xy2236-=,即xy27=,其中93≤≤x.OABPCD[例证明:作DN∥EC,交MF于N,则∠1=∠2,∠C=∠4由弦切角定理得:∠3=∠1 ∴∠2=∠3 ∴DN=DF由切割线定理,CBCACE⋅=2DADBDF⋅=2∵AC=DB ∴CB=DA ∴22DFCE=CE=DF∴CE=DN 又∵∠5=∠6 ∴DNMCEM∆≅∆(AAS)∴CM=MD[例3] 已知PT切⊙O于T,PBA为割线,交OC于D,CT为直径,若OC=BD=4cm,AD=3cm,求PB长。
解:设TD=x ,BP=y ,由相交弦定理得:TD CD DB AD ⋅=⋅ 即x x )8(43-=⨯ 61=x ,22=x (舍)由切割线定理,BP AP PT ⋅=2 由勾股定理,222TD PT PD += ∴ 22TD BP AP PD +⋅= ∴ )7(6)4(22++=+y y y ∴ y =[例4] F ,若BC=9,解:连AB ,∴ ∠1=∴EF CE =由切割线定理得:1441692=⨯=⋅=CF CB AC ∴ AC=12[例5] P 为弦AB 上一点,C 在圆O 上,OP ⊥PC ,求证:(1)PB PA PC ⋅=2(2)若证明:(1)延长CP解:(2)易知321==OC PM ,设x AP =,y MB = 由相交弦定理,MN CM MB AM ⋅=⋅,即27)63(3)3(=+⨯=+y x ① 由垂径定理,CP=PD ,故在CPO Rt ∆中有2046222=-=PC ∴ 由(1)结论,20)3(=+y x ② 由①—②得:37+=x y 代②得,0203162=-+x x ∴ 0601632=-+x x ,36128±-=x (舍负)∴ AP 长为36128+-[例6] 如图,AB 切⊙O 于B ,OB 交割线ACD 于E ,AC=CE=3,OE=25,求AB 长。

初三数学弦切角、相交弦定理、割线定理、切割线定理首师大版【同步教育信息】一. 本周教学内容:弦切角、相交弦定理、割线定理、切割线定理(一)弦切角:1. 定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
满足三个条件:(1)顶点在圆上;(2)一边和圆相交;(3)一边和圆相切。
判断下列图形中的∠BAC是不是弦切角:图A中,缺少“顶点在圆上”的条件;图B中,缺少“一边和圆相交”的条件;圆C中,缺少“一边和圆相切”的条件;圆D中,缺少“顶点在圆上”和“一边和圆相切”两个条件。
所以,图中的∠BAC都不是弦切角。
2. 分类(以圆心的位置分):(1)圆心在角的外部;(2)圆心在角的一边上;(3)圆心在角的内部。
3. 弦切角的度理定理:弦切角的度数等于它所夹的弧的度数的一半。
推论1:弦切角定理:弦切角等于它所夹的弧对的圆周角。
推论2:在同圆或等圆中,如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。
(二)相交弦定理圆的两条弦相交,被交点分成的两条线段长的积相等。
如图1(1),在⊙O中,AB、CD相交于点P,则PA·PB=PC·PD。
(三)割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
如图1(3),有PA·PB=PC·PD。
(四)切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
如图1(4),有PA2=PC·PD。
当点P从圆内运动到圆上、圆外时(从图1(1)到图1(3)),总有PA·PB=PC·PD,图1(2)中,点B、D与点P重合,PB=PD=0,PA·PB=PC·PD同样成立。
当割线PBA绕着点P旋转到切线PA的位置时,点B与A重合,结论不变,仍有PA·PB =PC·PD,此时PA=PB,所以PA2=PC·PD。

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段[学习目标]1. 切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
2. 切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
直线AB切OO于P, PG PD为弦,图中几个弦切角呢?(四个)4. 弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5. 弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6. 遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
已知OO 中,AB CD为弦,交PA- PB= PG- PD. 连结AG、BD, 证:于P.△ APS A DPB.结论证法OO 中,AB为直径,CDL ABPC= PA- PB. 于P. 用相交弦定理•3.弦切角:顶点在圆上,一边和圆相交,另2OO 中,割线PB 交OO 于P'C - P'D = r —延长P'O 交OO 于 M 延 2 A , CD 为弦 OP' 长OP'交OO 于N,用相交PA- PB= OP — r 2 弦定理证;过P 作切线用r 为OO 的半径 切割线定理勾股定理证8.圆幕定理:过一定点P 向OO 作任一直线,交OO 于两点,贝洎定点P 到两交点的两条线段之积为常数 |一_亠-| (R 为圆半径),因为OP 2 -R 2叫做点对于OO 的幕,所以将上述定理统称为圆幕定理。
切割线定 T , PT 2= PA - PB 连结 TA 、TB , 证: △ PTB^A PAT 理推论 PBPD 为OO 的两条割线,PA- PB= PC- PD 交OO 于A C 过P 作PT 切OO 于T ,用 两次切割线定理。
2.4&2.5 切割线定理 相交弦定理对应学生用书P23]1.切割线定理(1)文字语言:过圆外一点作圆的一条切线和一条割线,切线长是割线上从这点到两个交点的线段长的比例中项.(2)符号语言:从⊙O外一点P引圆的切线PT和割线PAB,T是切点,则PT2=PA·PB.(3)图形语言:如图所示.推论:过圆外一点作圆的两条割线,在一条割线上从这点到两个交点的线段长的积,等于另一条割线上对应线段长的积(割线定理).2.相交弦定理(1)文字语言:圆内的两条相交弦,被交点分成的两条线段长的积相等.(2)符号语言:⊙O的两条弦AB和CD相交于圆内的一点P,则PA·PB=PC·PD.(3)图形语言:如图所示.1.由相交弦定理知,垂直于弦的直径平分弦.那么,直径被弦分成的两条线段与弦有何关系?提示:弦的一半是直径被弦分成的两条线段的比例中项.2.如图,圆外一点P引圆的两条割线能否有PA·AB=PC·CD?提示:只有PA=PC时才有PA·PB=PC·CD成立.对应学生用书P23]切割线定理的应用[例1] 如图所示,⊙O1与⊙O2相交于A,B两点,AB是⊙O2的直径,过A点作⊙O1的切线交⊙O2于点E,并与BO1的延长线交于点P.PB分别与⊙O1,⊙O2交于C,D两点.求证:(1)PA·PD=PE·PC;(2)AD=AE.[思路点拨] 本题主要考查切割线定理的应用.解题时由割线定理得PA·PE=PD·PB,再由切割线定理知PA2=PC·PB可得结论,然后由(1)进一步可证AD=AE.[精解详析] (1)∵PAE,PDB分别是⊙O2的割线,∴PA·PE=PD·PB.①又∵PA,PCB分别是⊙O1的切线和割线,∴PA2=PC·PB.②由①②得PA·PD=PE·PC.(2)连接AD,AC,ED,∵BC是⊙O1的直径,∴∠CAB=90°.∴AC是⊙O2的切线.又由(1)知=,∴AC∥ED.∴AB⊥ED.又∵AB是⊙O2∴AD=AE.讨论与圆有关的线段间的相互关系,常常可以借助于切割线定理和相似成比例的知识去解决,通常用分析法揭示解题的思考过程,而用综合法来表示解题的形式.1.(湖北高考)如图,P为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B.过PA 的中点Q作割线交⊙O于C,D两点.若QC=1,CD=3,则PB= .解析:由切割线定理,得QA2=QC·QD=4⇒QA=2,则PB=PA=2QA=4.答案:4相交弦定理的应用[例2]O于C,D两点,垂足是点E.求证:PC·PD=AE·AO.[思路点拨] 由相交弦定理知PC·PD=AP·PB,又P为AB的中点,所以PC·PD=AP2.在Rt△PAO中再使用射影定理即可.[精解详析] 连接OP,∵P为AB的中点,∴OP⊥AB,AP=PB.∵PE⊥OA,∴AP2=AE·AO.∵PD·PC=PA·PB=AP2,∴PD·PC=AE·AO.相交弦定理的运用多与相似三角形联系在一起,经常与射影定理、直角三角形的性质相结合证明某些结论.2.(湖南高考)如图,已知AB,BC是⊙O的两条弦,AO⊥BC,AB=,BC=2,则⊙O 的半径等于.解析:设AO,BC的交点为D,由已知可得D为BC的中点,则在直角三角形ABD中,AD==1,设圆的半径为r,延长AO交圆O于点E,由圆的相交弦定理可知BD·CD=AD·DE,即()2=2r-1,解得r=.答案:相交弦定理与切割线定理的综合应用[例3],AD、BC 相交于E点,F为CE上一点,且DE2=EF·EC.(1)求证:∠P=∠EDF;(2)求证:CE·EB=EF·EP.(3)若CE∶BE=3∶2,DE=6,EF=4,求PA的长.[思路点拨] 本题主要考查相交弦定理与切割线定理的综合应用.解题时先证△CED ∽△DEF,同时利用平行关系可证(1);然后证明△DEF∽△PEA,结合相交弦定理可证(2);最后由切割线定理可求PA.[精解详析] (1)证明:∵DE2=EF·EC,∴DE∶EC=EF∶ED.∵∠DEF是公共角,∴△CED∽△DEF.∴∠EDF=∠C.∵CD∥AP,∴∠C=∠P.∴∠P=∠EDF.(2)证明:∵∠P=∠EDF,∠DEF=∠PEA,∴△DEF∽△PEA.∴DE∶PE=EF∶EA,即EF·EP=DE·EA.∵弦AD,BC相交于点E,∴DE·EA=CE·EB.∴CE·EB=EF·EP.(3)∵DE2=EF·EC,DE=6,EF=4,∴EC=9.∵CE∶BE=3∶2,∴BE=6.∵CE·EB=EF·EP,∴9×6=4×EP.解得EP=.∴PB=PE-BE=,PC=PE+EC=.由切割线定理得PA2=PB·PC.∴PA2=×.∴PA=.解决与圆有关的线段问题多综合应用相交弦定理及切割线定理,同时注意相似三角形及平行过渡传递等量关系的应用.3.如图,E是⊙O内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于点F,FC与圆交于点G.求证:(1)△DFE∽△EFA;(2)△EFG∽△CFE.证明:(1)∵EF∥CB,∴∠DEF=∠DCB.∵∠DCB和∠DAB都是»DB上的圆周角,∴∠DAB=∠DCB=∠DEF.∵∠DFE=∠EFA,∴△DFE∽△EFA.(2)由(1)知:△DFE∽△EFA,∴=.即EF2=FA·FD.由割线定理得FA·FD=FG·FC.∴EF2=FG·FC,即=.又∵∠EFG=∠CFE,∴△EFG∽△CFE.本课时主要考查相交弦定理、切割线定理的应用.难度中档,是高考命题的热点内容.[考题印证](新课标全国卷Ⅱ)如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E.证明:(1)BE=EC;(2)AD·DE=2PB2.[命题立意] 本题主要考查切割线定理、相交弦定理以及三角形的外切定理、弦切角定理、同弧所对的圆心角相等定理.[自主尝试] (1)连接AB,AC.由题设知PA=PD,故∠PAD=∠PDA.因为∠PDA=∠DAC+∠DCA,∠PAD=∠BAD+∠PAB,∠DCA=∠PAB,所以∠DAC=∠BAD,因此BE=EC.(2)由切割线定理得PA2=PB·PC.因为PA=PD=DC,所以DC=2PB,BD=PB.由相交弦定理得AD·DE=BD·DC,所以AD·DE=2PB2.对应学生用书P25]一、选择题1.如图,已知⊙O的两条弦AB,CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为( )A.4 B.5C.8 D.10解析:选B 设CE=x,则DE=3+x.根据相交弦定理,得x(x+3)=2×2,x=1或x=-4(不合题意,应舍去).则CD=3+1+1=5.2.如图,点P是⊙O外一点,PAB为⊙O的一条割线,且PA=AB,PO交⊙O于点C,若OC=3,OP=5,则AB的长为( )A. B.2C. D.解析:选B 设PA=AB=x,延长PO交圆于点D.因为PA·PB=PC·PD,OC=3,OP=5,所以PC=2,PD=8.所以x·2x=16,所以x=2.3.如图,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E,则( )A.CE·CB=AD·DB B.CE·CB=AD·ABC.AD·AB=CD2D.CE·EB=CD2解析:选A 在直角三角形ABC中,根据直角三角形射影定理可得CD2=AD·DB,再根据切割线定理可得CD2=CE·CB,所以CE·CB=AD·DB.4.如图,CA,CD分别切圆O1于A,D两点,CB,CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB,CD,CE的长度,下列关系正确的是( )A.AB>CE>CD B.AB=CE>CDC.AB>CD>CE D.AB=CD=CE解析:选A 因为∠1=60°,∠2=65°,所以∠ABC=180°-∠1-∠2=180°-60°-65°=55°,所以∠2>∠1>∠ABC,所以AB>BC>AC,因为CA,CD分别切圆O1于A,D两点,CB,CE分别切圆O2于B,E两点,所以AC=CD,BC=CE,所以AB>CE>CD.故选A.二、填空题5.如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2,AB=3,则BD的长为.解析:由切割线定理得:DB·DA=DC2,即DB(DB+BA)=DC2,∴DB2+3DB-28=0,∴DB=4.答案:46.如图,从圆O外一点P引圆O的切线PA和割线PBC,已知PA=2,PC=4,圆心O到BC的距离为,则圆O的半径为.解析:记圆O的半径为R.依题意得PA2=PB·PC,PB==2,BC=PC-PB=2,所以R==2.答案:27.如图,⊙O的弦ED,CB的延长线交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=;CE= .解析:由切割线定理得AB·AC=AD·AE,即4×6=3×(3+DE),解得DE=5;易知==,又∠A=∠A,故△ABD∽△AEC,故∠BCE=∠BDA=90°,=.在直角三角形ABD中,BD==,∴CE===2.答案:5 28.如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=,AF∶FB∶BE=4∶2∶1.若CE与圆相切,则线段CE的长为.解析:设BE=x,则FB=2x,AF=4x,由相交弦定理得DF·FC=AF·FB,即2=8x2,解得x=,AE=,再由切割线定理得CE2=EB·EA=×=,所以CE=.答案:三、解答题9.如图,P为圆O外一点,PA,PB是圆O的两条切线,A,B为切点,OP与AB相交于点M,且点C求证:∠OPC=∠OCM.证明:连接OB,由切线长定理,得PA=PB,PM⊥AB,PO平分∠APB.又PB⊥OB,在Rt△OPB中,OB2=OP·OM,∵OB=OC,∴OC2=OP·OM,即=,∴△OCP∽△OMC,∴∠OPC=∠OCM.10.如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.(1)求BD的长.(2)求∠ABE+2∠D的度数.(3)求的值.解:(1)连接OC,因为AB是小圆的切线,C是切点,所以OC⊥AB,所以C是AB的中点.因为AD是大圆的直径,所以O是AD的中点.所以OC是△ABD的中位线.所以BD=2OC=10.(2)连接AE.由(1)知C是AB的中点.同理F是BE的中点.即AB=2BC,BE=2BF,由切线长定理得BC=BF.所以BA=BE.所以∠BAE=∠E.因为∠E=∠D,所以∠ABE+2∠D=∠ABE+∠E+∠BAE=180°.(3)连接BO,在Rt△OCB中,因为OB=13,OC=5,所以BC=12,AB=24.由(2)知∠OBG=∠OBC=∠OAC.因为∠BGO=∠AGB,所以△BGO∽△AGB.所以==.11.如图,在Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.(1)若∠E=30°,求证:BC·BD=r·ED.(2)若BD=3,DE=4,求AE的长.解:(1)证明:取AB的中点为O,△ABC是直角三角形,AB是斜边,O是外接圆的圆心,连接CO,所以BO=CO,∠BCO=∠OBC,因为BC是∠DBE的平分线,所以∠DBC=∠CBA,所以∠OCB=∠DBC,所以OC∥DB(内错角相等,两直线平行),所以=,把比例式化为乘积式得BD·CE=DE·OC,因为OC=r,所以BD·CE=DE·r.因为∠D=90°,∠E=30°,所以∠DBE=60°,所以∠CBE=∠DBE=30°,所以∠CBE=∠E,所以CE=BC,所以BC·BD=r·ED.(2)过点C作CH⊥OE,垂足为H.BD=3,DE=4,根据勾股定理,BE=5,OC=OA =r,因为OC∥DB,所以△OCE∽△BDE,所以==,即==,解得OE=r,CE=r.CH==r,因为BC平分∠DBE交DE于点C,则△BDC≌△BHC,所以BH=BD=3,则HE=2.在Rt△CHE中,根据勾股定理得:CH2+EH2=CE2,即2+22=2,解得:r=,则AE=BE-2r=5-=.。
圆中的重要模型--圆幂定理模型圆幂定理是一个总结性的定理,是对相交弦定理、切割线定理、割线定理、弦切角定理、托勒密定理以及它们推论的统一与归纳。
可能是在19世纪由德国数学家施泰纳(Steiner)或者法国数学家普朗克雷(Poncelet)提出的。
圆幂定理的用法:可以利用圆幂定理求解与圆有关的线段比例、角度、面积等问题。
模型1.相交弦模型条件:在圆O中,弦AB与弦CD交于点E,点E在圆O内。
结论:△CAE∼△BDE⇒ECEB=EAED⇒EC⋅ED=EB⋅EA。
1(2023·广东广州·九年级校考期中)如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,两圆组成的圆环的面积是.2(2023·江西景德镇·九年级校考期末)如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB=.3(2023·江苏·九年级专题练习)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(1)为了说明相交弦定理正确性,需要对其进行证明,如下给出了不完整的“已知”“求证”,请补充完整,并写出证明过程.已知:如图①,弦AB,CD交于点P,求证:.(2)如图②,已知AB是⊙O的直径,AB与弦CD交于点P,且AB⊥CD于点P,过D作⊙O的切线,交BA的延长线于E,D为切点,若AP=2,⊙O的半径为5,求AE的长.模型2.双割线模型条件:如图,割线CH与弦CF交圆O于点E和点G。
结论:△CEG∼△CHF⇒ECCH=CGCF⇒EC⋅FC=GC⋅HC4(2023·浙江·九年级假期作业)如图:PAB、PCD为⊙O的两条割线,若PA∙PB=30,PC=3,则CD的长为()A.10B.7C.510D.35(2023·四川成都·九年级校考阶段练习)如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为.6(2022·河南洛阳·统考一模)我们知道,直线与圆有三种位置关系:相交、相切、相离.当直线与圆有两个公共点(即直线与圆相交)时,这条直线就叫做圆的割线.割线也有一些相关的定理.比如,割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等.下面给出了不完整的定理“证明一”,请补充完整.已知:如图①,过⊙O 外一点P 作⊙O 的两条割线,一条交⊙O 于A 、B 点,另一条交⊙O 于C 、D 点.求证:PA ⋅PB =PC ⋅PD .证明一:连接AD 、BC ,∵∠A 和∠C 为BD 所对的圆周角,∴.又∵∠P =∠P ,∴,∴.即PA ⋅PB =PC ⋅PD .研究后发现,如图②,如果连接AC 、BD ,即可得到学习过的圆内接四边形ABDC .那么或许割线定理也可以用圆内接四边形的性质来证明.请根据提示,独立完成证明二.证明二:连接AC 、BD ,模型3.切割线模型条件:如图,CB 是圆O 的切线,CA 是圆O 的割线。
1.弦切角定理(1)弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.(2)弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半.如图所示,直线PT切圆O于点C,BC、AC为圆O的弦,则有∠PCA=∠PBC(∠PCA为弦切角).2、相交弦定理【结论1】如图,⊙O中,弦AB、CD相交于点P,半径为r,则①AP·BP=CP·DP,②AP·BP=CP·DP=r2-OP2.3、切割线定理【结论2】如图,PBC是⊙O的一条割线,PA是⊙O的一条切线,切点为A,半径为r,则①PA2=PB·PC,②PA2=PB·PC=PO2-r24、割线定理【结论3】如图,PAB、PCD是⊙O的两条割线,半径为r,则①PA·PB=PC·PD②PA·PB=PC·PD=OP2-r2☑口诀:从两线交点处引出的共线线段的乘积相等例题精讲考点一:相交弦定理【例1】.已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于()A.B.C.D.变式训练【变式1-1】.如图,⊙O的弦AB、CD相交于点E,若CE:BE=2:3,则AE:DE=.【变式1-2】.如图,在⊙O的内接四边形ABCD中,AC⊥BD,CA=CB,过点A作AC的垂线交CD的延长线于点E,连结BE.若cos∠ACB=,则的值为.考点二:弦切角定理【例2】.如图,割线PAB过圆心O,PD切⊙O于D,C是上一点,∠PDA=20°,则∠C的度数是度.变式训练【变式2-1】.如图,已知∠P=45°,角的一边与⊙O相切于A点,另一边交⊙O于B、C两点,⊙O的半径为,AC=,则AB的长度为()A.B.6C.D.5【变式2-2】.如图,BP是⊙O的切线,弦DC与过切点的直径AB交于点E,DC的延长线和切线交于点P,连接AD,BC.若DE=DA=,BC=2,则线段CP的长为.考点三:切割线定理【例3】.如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为.变式训练【变式3-1】.如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OA为半径作圆O与BC相切于点D,分别交AC、AB于E、F,若CD=2CE=4,则⊙O的直径为()A.10B.C.5D.12【变式3-2】.如图,在四边形ABCD中,以AB为直径的半圆O经过点C,D.AC与BD相交于点E,CD2=CE•CA,分别延长AB,DC相交于点P,PB=BO,CD=2.则BO的长是.【变式3-3】.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.(1)求证:AC是△BDE的外接圆的切线;(2)若,求BD的长.考点四:割线定理【例4】.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,AB=PC=2,则PD的长是()A.3B.7.5C.5D.5.5变式训练【变式4-1】.如图,P是圆O外的一点,点B、D在圆上,PB、PD分别交圆O于点A、C,如果AP=4,AB=2,PC=CD,那么PD=.【变式4-2】.已知直角梯形ABCD的四条边长分别为AB=2,BC=CD=10,AD=6,过B、D两点作圆,与BA的延长线交于点E,与CB的延长线交于点F,则BE﹣BF的值为.1.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,CM切⊙O于点C,∠BCM=60°,则∠B的正切值是()A.B.C.D.2.如图,从圆外一点P引圆的切线PA,点A为切点,割线PDB交⊙O于点D、B.已知PA=12,PD=8,则S△ABP:S△DAP=.3.如图,在△ABC中,AB=AC,∠C=72°,⊙O过AB两点且与BC切于B,与AC交于D,连接BD,若BC=﹣1,则AC=.4.如图,⊙O的直径AB=8,将弧BC沿弦BC折叠后与∠ABC的角平分线相切,则△ABC 的面积为.5.如图,⊙O是△ABC的外接圆,∠BAC=45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则DE的长是.6.如图,已知AC=AB,AD=5,DB=4,∠A=2∠E.则CD•DE=.7.如图:BE切⊙O于点B,CE交⊙O于C,D两点,且交直径于AB于点P,OH⊥CD于H,OH=5,连接BC、OD,且BC=BE,∠C=40°,劣弧BD的长是.8.如图,在平面直角坐标系中,⊙O经过点A(4,3),点B与点C在y轴上,点B与原点O重合,且AB=AC,AC与⊙O交于点D,延长AO与⊙O交于点E,连接CE、DE 与x轴分别交于点G、F,则tan∠DFO=,tan∠A=.9.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,CD是⊙O的切线,C为切点,且CD=CB,连接AD,与⊙O交于点E.(1)求证AD=AB;(2)若AE=5,BC=6,求⊙O的半径.10.如图,△ABC是⊙O的内接三角形,CD是⊙O的直径,AB⊥CD于点E,过点A作⊙O 的切线交CD的延长线于点F,连接FB.(1)求证:FB是⊙O的切线.(2)若AC=4,tan∠ACD=,求⊙O的半径.11.如图,正方形ABCD内接于⊙O,点E为AB的中点,连接CE交BD于点F,延长CE 交⊙O于点G,连接BG.(1)求证:FB2=FE•FG;(2)若AB=6,求FB和EG的长.12.如图,⊙O的割线PBA交⊙O于A、B,PE切⊙O于E,∠APE的平分线和AE、BE 分别交于C、D,PE=4,PB=4,∠AEB=60°.(1)求证:△PDE∽△PCA;(2)试求以PA、PB的长为根的一元二次方程;(3)求⊙O的面积.(答案保留π)13.如图,圆O上有A,B,C三点,AC是直径,点D是的中点,连接CD交AB于点E,点F在AB延长线上,且FC=FE.(1)求证:CF是圆O的切线;(2)若,BE=2,求圆O的半径和DE•EC的值.14.如图,AB为⊙O的直径,点P在AB的延长线上,点C在⊙O上,且PC2=PB•PA.(1)求证:PC是⊙O的切线;(2)已知PC=20,PB=10,点D是的中点,DE⊥AC,垂足为E,DE交AB于点F,求EF的长.15.已知:如图,PF是⊙O的切线,PE=PF,A是⊙O上一点,直线AE、AP分别交⊙O于B、D,直线DE交⊙O于C,连接BC,(1)求证:PE∥BC;(2)将PE绕点P顺时针旋转,使点E移到圆内,并在⊙O上另选一点A,如图2.其他条件不变,在图2中画出完整的图形.此时PE与BC是否仍然平行?证明你的结论.16.已知△ABC是⊙O的内接三角形,∠BAC的平分线与⊙O相交于点D,连接DB.(1)如图①,设∠ABC的平分线与AD相交于点I,求证:BD=DI;(2)如图②,过点D作直线DE∥BC,求证:DE是⊙O的切线;(3)如图③,设弦BD,AC延长后交⊙O外一点F,过F作AD的平行线交BC的延长线于点G,过G作⊙O的切线GH(切点为H),求证:FG=HG.17.【提出问题】小聪同学类比所学的“圆心角“与“圆周角”的概念,将顶点在圆内(顶点不在圆心)的角命名为圆内角.如图1中,∠AEC,∠BED就是圆内角,所对的分别是、,那么圆内角的度数与所对弧的度数之间有什么关系呢?【解决问题】小聪想到了将圆内角转化为学过的两种角,即圆周角、圆心角,再进一步解决问题:解:连接BC,OA,OC,OB,OD.如图2,在△BCE中,∠AEC=∠EBC+∠ECB∵∠EBC=∠AOC,∠ECB=∠BOD∴∠AEC=∠AOC+∠BOD=(∠AOC+∠BOD)即:∠AEC的度数=(的度数+的度数)(1)如图1,在⊙O中,弦AB、CD相交于点E,若弧的度数是65°,弧的度数是40°,则∠AED的度数是.【类比探究】顶点在圆外且两边与圆相交的角,命名为圆外角.(2)如图3,在⊙O中,弦AB,CD的延长线相交于点E,试探索圆外角∠E的度数与它所夹的两段弧、的度数之间的关系.【灵活运用】(3)如图4,平面直角坐标系内,点A(,1)在⊙O上,⊙O与y轴正半轴交于点B,点C,点D是线段OB上的两个动点,满足AC=AD.AC,AD的延长线分别交⊙O 于点E、F.延长FE交y轴于点G,试探究∠FGO的度数是否变化.若不变,请求出它的度数;若变化,请说明理由.。
相交弦定理、切割线定理是什么初中还是高中的知识相交弦定理、切割线定理是什么初中还是高中的知识是初中知识。
【相交线定理】圆内两条弦AB、CD相交于圆内一点P,则:PA×PB=PC×PD【切割线定理】过圆外一点P,作圆的割线PAB、PCD,和圆的切线PT,则:PA×PB=PC×PD=PT²急!圆的切割线定理和相交弦定理是什么1、相交弦定理。
设AB和CD是圆内的两条相交弦,交点为P,则PA×PB=PC×PD;2、切割线定理。
过圆外一点P,作圆的切线PT和割线PAB,切点为T,割线与圆的交点为A、B,则PT²=PA×PB。
能具体说说割线定理,切割线定理,相交弦定理吗?切割线定理如图:hiphotos.baidu./get%5Fon/pic/item/e39387f9d1672352252d f291.jpg, ABT是⊙O的一条割线,TC是⊙O的一条切线,切点为C,则TC2=TA·TB 证明:连接AC、BC ∵弦切角∠TCB对弧BC,圆周角∠A对弧BC ∴由弦切角定理,得∠TCB=∠A 又∠ATC=∠BTC ∴△ACT∽△CBT ∴AT:CT=CT:BT, 也就是CT2=AT·BT 割线定理如图:hiphotos.baidu./get%5Fon/pic/item/e3a17897b3a27e6655fb 9691.jpg,直线ABP和CDT是自点P引的⊙O的两条割线,则PA·PB=PC·PD 证明:连接AD、BC ∵∠A和∠C都对弧BD ∴由圆周角定理,得∠A=∠C 又∵∠APD=∠CPB ∴△ADP∽△CBP ∴AP:CP=DP:BP, 也就是AP·BP=CP·DP什么叫相交弦定理?什么叫切割线定理相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的乘积相等证明:连结AC,BD,由圆周角定理的推论,得∠A=∠D,∠C=∠B。