实验一_时域离散信号、系统及系统响应

实验一 信号、系统及系统响应一、实验目的1、熟悉理想采样的性质，了解信号采样前后的频谱变化，加深对时域采样定理的理解。

2、熟悉离散信号和系统的时域特性。

3、熟悉线性卷积的计算编程方法：利用卷积的方法，观察、分析系统响应的时域特性。

4、掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对离散信号、系统及其系统响应进行频域分析。

二、 实验原理1.理想采样序列：对信号x a (t)=A e −αt sin(Ω0t )u(t)进行理想采样，可以得到一个理想的采样信号序列x a (t)=A e −αt sin(Ω0nT ),0≤n ≤50，其中A 为幅度因子，α是衰减因子，Ω0是频率，T 是采样周期。

2.对一个连续时间信号x a (t)进行理想采样可以表示为该信号与一个周期冲激脉冲的乘积，即x ̂a (t)= x a (t)M(t),其中x ̂a (t)是连续信号x a (t)的理想采样；M(t)是周期冲激M(t)=∑δ+∞−∞(t-nT)=1T ∑e jm Ωs t +∞−∞,其中T 为采样周期，Ωs =2π/T 是采样角频率。

信号理想采样的傅里叶变换为X ̂a (j Ω)=1T ∑X a +∞−∞[j(Ω−k Ωs )],由此式可知：信号理想采样后的频谱是原信号频谱的周期延拓，其延拓周期为Ωs =2π/T 。

根据时域采样定理，如果原信号是带限信号，且采样频率高于原信号最高频率分量的2倍，则采样以后不会发生频率混叠现象。

三、简明步骤产生理想采样信号序列x a (n),使A=444.128，α=50√2π，Ω0=50√2π。

（1） 首先选用采样频率为1000HZ ，T=1/1000，观察所得理想采样信号的幅频特性，在折叠频率以内和给定的理想幅频特性无明显差异，并做记录；（2） 改变采样频率为300HZ ，T=1/300，观察所得到的频谱特性曲线的变化，并做记录；（3） 进一步减小采样频率为200HZ ，T=1/200，观察频谱混淆现象是否明显存在，说明原因，并记录这时候的幅频特性曲线。

第1篇一、实验目的1. 理解时域离散信号的基本概念和特性。

2. 掌握时域离散信号的表示方法。

3. 熟悉常用时域离散信号的产生方法。

4. 掌握时域离散信号的基本运算方法。

5. 通过MATLAB软件进行时域离散信号的仿真分析。

二、实验原理时域离散信号是指在时间轴上取离散值的一类信号。

这类信号在时间上不连续，但在数值上可以取到任意值。

时域离散信号在数字信号处理领域有着广泛的应用，如通信、图像处理、语音处理等。

时域离散信号的基本表示方法有：1. 序列表示法：用数学符号表示离散信号，如 \( x[n] \) 表示离散时间信号。

2. 图形表示法：用图形表示离散信号，如用折线图表示序列。

3. 时域波形图表示法：用波形图表示离散信号，如用MATLAB软件生成的波形图。

常用时域离散信号的产生方法包括：1. 单位阶跃信号：表示信号在某个时刻发生突变。

2. 单位冲激信号：表示信号在某个时刻发生瞬时脉冲。

3. 正弦信号：表示信号在时间上呈现正弦波形。

4. 矩形脉冲信号：表示信号在时间上呈现矩形波形。

时域离散信号的基本运算方法包括：1. 加法：将两个离散信号相加。

2. 乘法：将两个离散信号相乘。

3. 卷积：将一个离散信号与另一个离散信号的移位序列进行乘法运算。

4. 反褶：将离散信号沿时间轴翻转。

三、实验内容1. 实验一：时域离散信号的表示方法（1）使用序列表示法表示以下信号：- 单位阶跃信号：\( u[n] \)- 单位冲激信号：\( \delta[n] \)- 正弦信号：\( \sin(2\pi f_0 n) \)- 矩形脉冲信号：\( \text{rect}(n) \)（2）使用图形表示法绘制以上信号。

2. 实验二：时域离散信号的产生方法（1）使用MATLAB软件生成以下信号：- 单位阶跃信号- 单位冲激信号- 正弦信号（频率为1Hz）- 矩形脉冲信号（宽度为2）（2）观察并分析信号的波形。

3. 实验三：时域离散信号的基本运算（1）使用MATLAB软件对以下信号进行加法运算：- \( u[n] \)- \( \sin(2\pi f_0 n) \)（2）使用MATLAB软件对以下信号进行乘法运算：- \( u[n] \)- \( \sin(2\pi f_0 n) \)（3）使用MATLAB软件对以下信号进行卷积运算：- \( u[n] \)- \( \sin(2\pi f_0 n) \)（4）使用MATLAB软件对以下信号进行反褶运算：- \( u[n] \)4. 实验四：时域离散信号的仿真分析（1）使用MATLAB软件对以下系统进行时域分析：- 系统函数：\( H(z) = \frac{1}{1 - 0.5z^{-1}} \)（2）观察并分析系统的单位冲激响应。

数字信号处理课程实验报告实验一 离散时间信号和系统响应一. 实验目的1. 熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解2. 掌握时域离散系统的时域特性3. 利用卷积方法观察分析系统的时域特性4. 掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对离散信号及系统响应进行频域分析二、实验原理1. 采样是连续信号数字化处理的第一个关键环节。

对采样过程的研究不仅可以了解采样前后信号时域和频域特性的变化以及信号信息不丢失的条件，而且可以加深对离散傅里叶变换、Z 变换和序列傅里叶变换之间关系式的理解。

对连续信号()a x t 以T 为采样间隔进行时域等间隔理想采样，形成采样信号： 式中()p t 为周期冲激脉冲，()a x t 为()a x t 的理想采样。

()a x t 的傅里叶变换为()a X j Ω：上式表明将连续信号()a x t 采样后其频谱将变为周期的，周期为Ωs=2π/T 。

也即采样信号的频谱()a X j Ω是原连续信号xa(t)的频谱Xa(jΩ)在频率轴上以Ωs 为周期，周期延拓而成的。

因此，若对连续信号()a x t 进行采样，要保证采样频率fs ≥2fm ，fm 为信号的最高频率，才可能由采样信号无失真地恢复出原模拟信号ˆ()()()a a xt x t p t =1()()*()21()n a a a s X j X j P j X j jn T π∞=-∞Ω=ΩΩ=Ω-Ω∑()()n P t t nT δ∞=-∞=-∑计算机实现时，利用计算机计算上式并不方便，因此我们利用采样序列的傅里叶变换来实现，即而()()j j n n X e x n e ωω∞-=-∞=∑为采样序列的傅里叶变换2. 时域中，描述系统特性的方法是差分方程和单位脉冲响应，频域中可用系统函数描述系统特性。

已知输入信号，可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应。

实验一时域离散信号的产生及时域处理实验目的：了解Matlab软件数字信号处理工具箱的初步使用方法。

掌握其简单的Matlab语言进行简单的时域信号分析。

实验内容：[1.1]已知两序列x1=[0,1,2,3,4,3,2,1,0];n1=[-2:6];x2=[2,2,0,0,0,-2,-2],n2=[2:8].求他们的和ya及乘积yp. 程序如下：x1=[0,1,2,3,4,3,2,1,0];ns1=-2;x2=[2,2,0,0,0,-2,-2];ns2=2;nf1=ns1+length(x1)-1;nf2=ns2+length(x2)-1;ny=min(ns1,ns2):max(nf1,nf2);xa1=zeros(1,length(ny));xa2=xa1;xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1;xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2;ya=xa1+xa2yp=xa1.*xa2subplot(4,4,1),stem(ny,xa1,'.')subplot(4,1,2),stem(ny,xa2,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,3),stem(ny,ya,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,4),stem(ny,yp,'.')line([ny(1),ny(end)],[0,0])[1.2]编写产生矩形序列的程序。

并用它截取一个复正弦序列，最后画出波形。

程序如下：clear;close alln0=input('输入序列起点:n0=');N=input('输入序列长度:N=');n1=input('输入位移:n1=');n=n0:n1+N+5;u=[(n-n1)>=0];x1=[(n-n1)>=0]-[(n-n1-N)>=0];x2=[(n>=n1)&(n<(N+n1))];x3=exp(j*n*pi/8).*x2;subplot(2,2,1);stem(n,x1,'.');xlabel('n');ylabel('x1(n)');axis([n0,max(n),0,1]);subplot(2,2,3);stem(n,x2,'.');xlabel('n');ylabel('x2(n)');axis([n0,max(n),0,1]);subplot(2,2,2);stem(n,real(x3),'.'); xlabel('n');ylabel('x3(n)的实部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);subplot(2,2,4);stem(n,imag(x3),'.'); xlabel('n');ylabel('x3(n)的虚部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);[1.3]利用已知条件，利用MATLAB生成图形。

实验一 离散时间信号及系统冲激响应和零状态响应一、 实验原理利用MATLAB 软件生成典型信号,通过系统差分方程求系统单位冲激响应，利用卷积计算给定输入的系统输出 二、 实验目的（1）熟悉MATLAB 软件的使用方法。

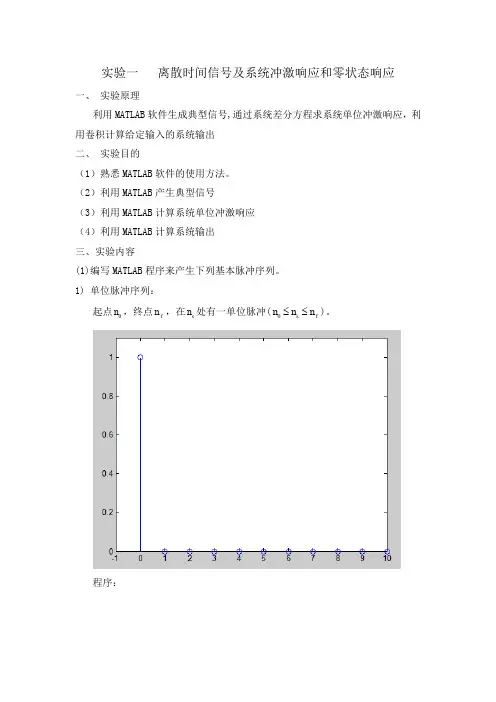
（2）利用MATLAB 产生典型信号（3）利用MATLAB 计算系统单位冲激响应 （4）利用MATLAB 计算系统输出 三、实验内容(1)编写MATLAB 程序来产生下列基本脉冲序列。

1) 单位脉冲序列：起点0n ，终点f n ，在s n 处有一单位脉冲(0s f n n n ≤≤)。

程序：2) 单位阶跃序列:起点0n ，终点f n ，在s n 前为0，在s n 处及以后为l(0s f n n n ≤≤)。

程序：3)实数指数序列：() 3()0.75n x n=程序：4)复数指数序列：(0.207) 4()j n x n e-+=程序：5)一个连续的锯齿波信号频率为1Hz，振幅值幅度为1V，在窗口上显示两个周期的信号波形，对它进行32点采样获得离散信号，试显示原信号和其采样获得离散信号波形。

程序：(2) ()0.75(1)0.125(2)()(1)y n y n y n x n x n+-+-=--表示线性时不变系统，用MATLAB求其冲激响应和阶跃响应程序：(3)用MATLAB 计算线性时不变系统()0.8(1)0.15y n y n x n--=当输入为1()2s i n (0.05)x n n π=时的零状态响应。

程序：(4) 用MATLAB计算线性时不变系统()0.9(1)()--=，当输入为y n y n x n =--时系统的零状态响应x n u n u n()()(10】程序：。

北华大学数字信号实验实验项目：信号、系统及系统响应班级：信息10-1姓名：张慧学号：36实验一 信号、系统及系统响应一．实验目的1．熟悉理想采样的性质，了解信号采用前后的频谱变化，加深对采样定理的理解。

2．熟悉离散信号和系统的时域特性。

3．熟悉线性卷积的计算编程方法：利用卷积的方法，观察、分析系统响应的时域特性。

4．掌握序列傅氏变换的计算机实现方法，利用序列的傅氏变换对离散信号、系统及系统响应进行频域分析。

二．实验原理1．连续时间信号的采样)()()(ˆt M t x t xa a = 其中)(ˆt xa 是连续信号)(t x a 的理想采样，)(t M 是周期冲激脉冲 ∑+∞-∞=-=n nT t t M )()(δ它也可以用傅立叶级数表示为：∑+∞-∞=Ω=n tjm s e T t M 1)(其中T 为采样周期，T s /2π=Ω是采样角频率。

设)(s X a 是连续时间信号)(t x a 的双边拉氏变换，即有：⎰+∞∞--=dt e t x s X sta a )()( 此时理想采样信号)(ˆt x a 的拉氏变换为 ∑⎰+∞-∞=+∞∞--Ω-===m s a sta ajm s X T dt e t x s X )(1)(ˆ)(ˆ作为拉氏变换的一种特例，信号理想采样的傅立叶变换[]∑+∞-∞=Ω-Ω=Ωm s a a m j X T j X )(1)(ˆ∑+∞-∞=-=n nzn x z X )()(以ωj e 代替上式中的z ，就可以得到序列)(n x 的傅立叶变换 ∑+∞-∞=-=n nj j en x e X ωω)()(具有如下关系：Tj a e X j X Ω==Ωωω)()(ˆ信号卷积∑+∞-∞=-=*=m m n h m x n h n x n y )()()()()()()()(z H z X z Y =)()()(ωωωj j j e H e X e Y =三．实验内容及步骤1， 分析理想采样的特性。

信号与系统实验报告一、信号的时域基本运算1．连续时间信号的时域基本运算两实验之一实验分析：输出信号值就等于两输入信号相加（乘）。

由于b=2，故平移量为2时，实际是右移1，符合平移性质。

两实验之二心得体会：时域中的基本运算具有连续性，当输入信号为连续时，输出信号也为连续。

平移，伸缩变化都会导致输出结果相对应的平移伸缩。

2.离散时间信号的时域基本运算两实验之一实验分析：输出信号的值是对应输入信号在每个n值所对应的运算值，当进行拉伸变化后，n值数量不会变，但范围会拉伸所输入的拉伸系数。

两实验之二心得体会：离散时间信号可以看做对连续时间信号的采样，而得到的输出信号值，也可以看成是连续信号所得之后的采样值。

二、连续信号卷积与系统的时域分析1.连续信号卷积积分两实验之一实验分析：当两相互卷积函数为冲激函数时，所卷积得到的也是一个冲激函数，且该函数的冲激t值为函数x，函数y冲激t值之和。

两实验之二心得体会：连续卷积函数每个t值所对应的卷积和可以看成其中一个在k值取得的函数与另外一个函数相乘得到的一个分量函数，并一直移动k值直至最后，最后累和出来的最终函数便是所得到的卷积函数。

3.RC电路时域积分两实验之一实验分析：全响应结果正好等于零状态响应与零输入响应之和。

两实验之二心得体会：具体学习了零状态，零输入，全响应过程的状态及变化，与之前所学的电路知识联系在一起了。

三、离散信号卷积与系统的时域分析1.离散信号卷积求和两实验之一实验分析：输出结果的n值是输入结果的k号与另一个n-k的累和两实验之二心得体会：直观地观察到卷积和的产生，可以看成连续卷积的采样形式，从这个方面去想，更能深入地理解卷积以及采样的知识。

2.离散差分方程求解两实验之一实验分析：其零状态响应序列为0 0 4 5 7.5，零输入响应序列为2 4 5 5.5 5.75，全状态响应序列为2 4 9 10.5 13.25，即全状态=零输入+零状态。

两实验之二心得体会：求差分方程时，可以根据全状态响应是由零输入输入以及零状态相加所得，分开来求，同时也加深了自己对差分方程的求解问题的理解。

实验一信号、系统及系统响应一、实验目的认真复习采样理论、离散信号与系统、线性卷积、序列的z 变换及性质等有关内容；掌握离散时间序列的产生与基本运算，理解离散时间系统的时域特性与差分方程的求解方法，掌握离散信号的绘图方法；熟悉序列的z 变换及性质，理解理想采样前后信号频谱的变化。

二、实验内容a. 产生长度为500 的在[0,1]之间均匀分布的随机序列，产生长度为500 的均值为0 单位方差的高斯分布序列。

N=500;x=rand(1,N);subplot(1,2,1);plot(x);grid on;y=randn(1,N);subplot(1,2,2);plot(y);b. 线性时不变系统单位脉冲响应为h(n)=(0.9)n u(n)，当系统输入为x(n)=R10(n)时，求系统的零状态响应，并绘制波形图。

n=[1:1:1000];y=0.9.^n.*u(n);x=ones(1,10);z=conv(x,y);stem(z)axis([0 20 0 10]);c. 描述系统的差分方程为：y(n)-y(n-1)+0.9y(n-2)=x(n)，其中x(n)为激励，y(n)为响应。

计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位脉冲响应h(n)；计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位阶跃响应s(n)；由h(n)表征的这个系统是稳定系统吗？A=[1,-1,0.9];B=[1];hn=impz(B,A,20);subplot(2,9,1);plot(hn);hn=impz(B,A,30);subplot(2,9,2);plot(hn);hn=impz(B,A,40);subplot(2,9,3);plot(hn);hn=impz(B,A,50);subplot(2,9,4);plot(hn);hn=impz(B,A,60);subplot(2,9,5);plot(hn);hn=impz(B,A,70);subplot(2,9,6);plot(hn);hn=impz(B,A,80);subplot(2,9,7); plot(hn);hn=impz(B,A,90); subplot(2,9,8); plot(hn);hn=impz(B,A,100); subplot(2,9,9); plot(hn);sn1=ones(1,20); sn=filter(B,A,sn1); subplot(2,9,10); stem(sn);sn2=ones(1,30); sn=filter(B,A,sn2); subplot(2,9,11); stem(sn);sn3=ones(1,40); sn=filter(B,A,sn3); subplot(2,9,12); stem(sn);sn4=ones(1,50); sn=filter(B,A,sn4); subplot(2,9,13); stem(sn);sn5=ones(1,60); sn=filter(B,A,sn5); subplot(2,9,14); stem(sn);sn6=ones(1,70); sn=filter(B,A,sn6); subplot(2,9,15); stem(sn);sn7=ones(1,80); sn=filter(B,A,sn7); subplot(2,9,16); stem(sn);sn8=ones(1,90); sn=filter(B,A,sn8); subplot(2,9,17); stem(sn);sn9=ones(1,100); sn=filter(B,A,sn9); subplot(2,9,18); stem(sn);d. 序列x(n)=(0.8)n u(n)，求DTFT[x(n)]，并画出它幅度、相位，实部、虚部的波形图。

前言数字信号处理是一门理论和工程实践密切结合的课程。

为了加深对教学内容的理解，应在学习理论的同时，加强上机实验，深入理解和消化基本理论，锻炼初学者独立解决问题的能力。

本课程实验要求学生运用MATLAB编程完成一些数字信号处理的基本功能。

MATLAB是一高效的工程计算语言，它将计算、可视化和编程等功能集于一个易于使用的环境。

在MATLAB环境中描述问题计编制求解问题的程序时，用户可以按照符合人们科学思维的方式和数学表达习惯的语言形式来书写程序。

MATLAB广泛应用于工业，电子，医疗和建筑等众多领域。

其典型应用主要包括以下几个方面：数学计算；算法开发；数据采集；系统建模和仿真；数据分析和可视化科学和工程绘图；应用软件开发（包括用户界面）。

；实验1 用MATLAB产生时域离散信号一、.实验目的：1、了解常用时域离散信号及其特点2、掌握用MATLAB 产生时域离散信号的方法 二、.实验原理： 1、时域离散信号的概念在时间轴的离散点上取值的信号，称为离散时间信号。

通常，离散时间信号用x(n)表示，其幅度可以在某一范围内连续取值。

由于信号处理设备或装置（如计算机、专用的信号处理芯片等）均以有限位的二进制数来表示信号的幅度，因此，信号的幅度也必须离散化。

我们把时间和幅度均取离散值的信号称为时域离散信号或数字信号。

在MATLAB 语言中，时域离散信号可以通过编写程序直接产生。

2、常用时域离散信号的生成 1) 单位抽样序列 单位抽样序列的表示式为⎩⎨⎧=01)(n δ00≠=n n 或 ⎩⎨⎧=-01)(k n δ 0≠=n kn 以下三段程序分别用不同的方法来产生单位抽样序列。

例1-1 用MATLAB 的关系运算式来产生单位抽样序列。

n1= -5;n2=5;n0=0;n=n1:n2; x=[n==n0]; stem(n,x,'filled');axis([n1,n2,0,1.1*max(x)]); xlabel('时间(n)');ylabel('幅度x(n)');title('单位脉冲序列');运行结果如图1-1所示：时间(n)幅度x (n )单位脉冲序列图1-1例1-2 用zeros 函数和抽样点直接赋值来产生单位抽样序列。

《数字信号处理》 实验报告学院 专业 电子信息工程 班级 姓名 学号 时间实验一 时域离散信号与系统分析一、实验目的1、熟悉连续信号经理想采样后的频谱变化关系，加深对时域采样定理的理解。

2、熟悉时域离散系统的时域特性，利用卷积方法观察分析系统的时域特性。

3、学会离散信号及系统响应的频域分析。

4、学会时域离散信号的MATLAB 编程和绘图。

5、学会利用MATLAB 进行时域离散系统的频率特性分析。

二、实验内容1、序列的产生（用Matlab 编程实现下列序列（数组），并用stem 语句绘出杆图。

（要求标注横轴、纵轴和标题）（1）. 单位脉冲序列x(n)=δ（n ） （2）. 矩形序列x(n)=R N (n) ,N=10nδ(n )nR N (n )图1.1 单位脉冲序列 图1.2 矩形序列(3) . x(n)=e （0.8＋3j ）n ； n 取0－15。

4n|x (n )|201321111053 陈闽焜n<x (n )/R a d图1.3 复指数序列的 模 图1.4 复指数序列的 相角（4）. x(n)=3cos （0. 25πn ＋0.3π）＋2sin （0.125πn ＋0.2π） n 取0－15。

ny (n )图1.4 复合正弦实数序列（5）. 把第（3）小题的复指数x(n)周期化，周期20点，延拓3个周期。

4m|y (m )|201321111053 陈闽焜图1.5 第（3）的20点周期延拓杆图（6）. 假设x(n)= [1，－3，2，3，-2 ]， 编程产生以下序列并绘出杆图：y(n) y(n)= x(n)－2x(n+1)+x(n-1)+x(n-3)；5201321111053 陈闽焜图1.6 y(n)序列杆图（7）、编一个用户自定义matlab 函数，名为stepshf （n0，n1，n2）实现单位阶跃序列u[n －n1]。

其中位移点数n1在起点n0和终点n2之间任意可选。

自选3个入口参数产生杆图。

实验一信号与系统的时域分析一、实验目的1、熟悉与掌握常用的用于信号与系统时域仿真分析的MA TLAB函数;2、掌握连续时间与离散时间信号的MA TLAB产生,掌握用周期延拓的方法将一个非周期信号进行周期信号延拓形成一个周期信号的MA TLAB编程;3、牢固掌握系统的单位冲激响应的概念,掌握LTI系统的卷积表达式及其物理意义,掌握卷积的计算方法、卷积的基本性质;4、掌握利用MA TLAB计算卷积的编程方法,并利用所编写的MA TLAB程序验证卷积的常用基本性质;掌握MA TLAB描述LTI系统的常用方法及有关函数,并学会利用MATLAB求解LTI系统响应,绘制相应曲线。

基本要求:掌握用MA TLAB描述连续时间信号与离散时间信号的方法,能够编写MATLAB程序,实现各种信号的时域变换与运算,并且以图形的方式再现各种信号的波形。

掌握线性时不变连续系统的时域数学模型用MA TLAB描述的方法,掌握卷积运算、线性常系数微分方程的求解编程。

二、实验原理信号(Signal)一般都就是随某一个或某几个独立变量的变化而变化的,例如,温度、压力、声音,还有股票市场的日收盘指数等,这些信号都就是随时间的变化而变化的,还有一些信号,例如在研究地球结构时,地下某处的密度就就是随着海拔高度的变化而变化的。

一幅图片中的每一个象素点的位置取决于两个坐标轴,即横轴与纵轴,因此,图像信号具有两个或两个以上的独立变量。

在《信号与系统》课程中,我们只关注这种只有一个独立变量(Independent variable)的信号,并且把这个独立变量统称为时间变量(Time variable),不管这个独立变量就是否就是时间变量。

在自然界中,大多数信号的时间变量都就是连续变化的,因此这种信号被称为连续时间信号(Continuous-Time Signals)或模拟信号(Analog Signals),例如前面提到的温度、压力与声音信号就就是连续时间信号的例子。

数字信号处理实验报告实验一 信号、系统及系统响应一、实验目的(1) 熟悉连续信号经理想采样前后的频谱变化关系， 加深对时域采样定理的理解。

(2) 熟悉时域离散系统的时域特性。

(3) 利用卷积方法观察分析系统的时域特性。

(4) 掌握序列傅里叶变换的计算机实现方法， 利用序列的傅里叶变换对连续信号、 离散信号及系统响应进行频域分析。

二、实验原理与方法 1. 时域采样定理:对一个连续信号xa(t)进行理想采样的过程如下： xa1(t)=xa(t)p(t)其中xa1(t)为xa(t)的理想采样,p(t)为周期冲击脉冲。

xa1(t)的傅里叶变换Xa1(j Ω)为:11()[()]m Xa j Xa j m s T +∞=-∞Ω=Ω-Ω∑表明Xa1(j Ω)为Xa(j Ω)的周期延拓，其延拓周期为采样角频率（s Ω=2π/T ）。

离散信号和系统在时域均可用序列来表示。

2. LTI 系统的输入输出关系: y(n)=x(n)*h(n)=()()m x m h n m +∞=-∞-∑()()()j j j Y e X e H e ωωω=三、实验内容1. 分析采样序列的特性。

1) 取模拟角频w=70.7*pi rad/s ，采样频率fs=1000Hz>2w ，发现无频谱混叠现象。

2) 改变采样频率， fs=300 Hz<2w ，频谱产生失真。

3) 改变采样频率， fs=200Hz<2w，频谱混叠，产生严重失真2. 时域离散信号、系统和系统响应分析。

1) 观察信号xb(n)和系统hb(n)的时域和频域特性；利用线性卷积求信号xb(n)通过系统hb(n)的响应y(n)，比较所求响应y(n)和hb(n)的时域及频域特性，注意它们之间有无差别，绘图说明，并用所学理论解释所得结果。

2) 观察系统ha(n)对信号xc(n)的响应特性。

可发现：信号通过系统，相当于x(n)与系统函数h(n)卷积，时域卷积即对应频域函数相乘。

数字信号处理实验与课程设计教程实验一戴虹编班级：15通信A1姓名：马佳音学号：20154820112工学部计算机与信息工程学院2015年12月实验一信号、系统及系统响应一、实验目的1.掌握典型序列的产生方法。

2.掌握DFT的实现方法，利用DFT对信号进行频域分析。

3.熟悉连续信号经采样前后频谱的变化，加深对时域采样定理的理解。

4.分别利用卷积和DFT分析信号及系统的时域和频域特性，验证时域卷积定理。

二、实验环境1．Windows2000操作系统2．MATLAB6.0三、实验原理1.信号采样对连续信号x a(t)=Ae-at sin(Ω0t)u(t)进行采样，采样周期为T,采样点0≤n<50，得采样序列x a(n)= Ae-at sin(Ω0nT)δ(t-nT) 。

2.离散傅里叶变换(DFT)设序列为x(n),长度为N,则X(ej ωk)=DFT[x(n)]=∑-=10N n x(n) e -jωkn,其中ωk =k Mπ2(k=0,1,2,…,M-1),通常M>N,以便观察频谱的细节。

|X(e j ωk )|----x(n)的幅频谱。

4.连续信号采样前后频谱的变化^X a (j Ω)=)]([s m a m j X T 1Ω-Ω∑∞-∞=即采样信号的频谱^X a (j Ω)是原连续信号x a (t)的频谱X a (j Ω)沿频率轴，以周期 Ωs 重复出现，幅度为原来的 1/T 倍。

5. 采样定理由采样信号无失真地恢复原连续信号的条件，即采样定理为：模拟信号经过变换转换为数字信号进行采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率fs ，重复出现一次，由此采样信号无失真地恢复原连续信号。

6．时域卷积定理设离散线性时不变系统输入信号为x(n),单位脉冲响应为h(n),则输出信号y(n)= x(n)*h(n) ；由时域卷积定理，在频域中，Y(e j ω)=FT[y(n)]= FT[x(n)]FT[h(n)] 。

信号、系统及系统响应实验报告实验⼀信号、系统及系统响应⼀、实验⽬的１、熟悉理想采样的性质，了解信号采样前后的频谱变化,加深对采样定理的理解。

2、熟悉离散信号和系统的时域特性；3、熟悉线性卷积的计算编程⽅法;利⽤卷积的⽅法,观察、分析系统响应的时域特性。

4、掌握序列傅⽒变换的计算实现⽅法,利⽤序列的傅⽒变换离散信号、系统及系统响应做频域分析。

⼆、实验原理(⼀）连续时间信号的采样对⼀个连续时间信号进⾏理想采样的过程可以表⽰为该信号的⼀个周期冲击脉冲的乘积，即()()()a a x t x t M t ∧= （1-1)其中()a x t ∧是连续信号()a x t 的理想采样，()M t 是周期冲激脉冲()()M t t nT δ+∞-∞=-∑ (1-２)理想信号的傅⾥叶变换为:1()[()]a a s m X j X j m T +∞∧=-∞Ω=Ω-Ω∑ (1-3）(⼆）有限长序分析⼀般来说，在计算机上不可能，也不必要处理连续的曲线()j X e ω，通常我们只要观察。

分析()j X e ω在某些频率点上的值。

对于长度为N 的有限长序列⼀般只需要在02π之间均匀的取M 个频率点。

(三）信号卷积⼀个线性时不变离散系统的响应y(ｎ)可以⽤它的单位冲激响应h(n 和输⼊信号ｘ(ｎ）的卷积来表⽰: ()()()()()m y n x n h n x m h n m +∞=-∞=*=-∑ (1-4)根据傅⾥叶变换和Ｚ变换的性质,与其对应应该有：()()()Y z X z H z = (1－5) ()()()j j j Y e X e H e ωωω= (1-6)式(1-3）可知通过对两个序列的移位、相乘、累加计算信号响应;⽽由式(１-６)可知卷积运算也可以在频域上⽤乘积实现。

三、实验内容及步结果1、分析理想采样信号序列的特性。

产⽣理想采样信号序列()a x t ,使Ａ=444.128，α=,0Ω=。

当频率fs ＝1000h ｚ时，其幅频特性如图1.1所⽰：-2000200理想采样信号序列（fs=1000hz ）时间幅值0100200理想采样信号序列幅度谱时间幅值-505理想采样信号序列相位谱频率幅值图1.１当fs=3００ｈｚ的时候,其幅频特性如图１．2所⽰:理想采样信号序列（fs=300hz ）时间幅值理想采样信号序列幅度谱时间幅值102030405060理想采样信号序列相位谱频率幅值图1.2当f ｓ=２００hz 的时候，其幅频特性如图１.3所⽰:理想采样信号序列（fs=200hz ）时间幅值理想采样信号序列幅度谱时间幅值理想采样信号序列相位谱频率幅值图1.3经过对⽐以上三个图形可以看出:当频率分别为1000h ｚ,３０0ｈｚ和200ｈz 的时候均没有出现混叠现象，因为给定的信号序列的频率为0Ω=，三个抽样频率均满⾜2s f f ≥，因此不会出现频率混叠现象。