模板18 线性回归方程.

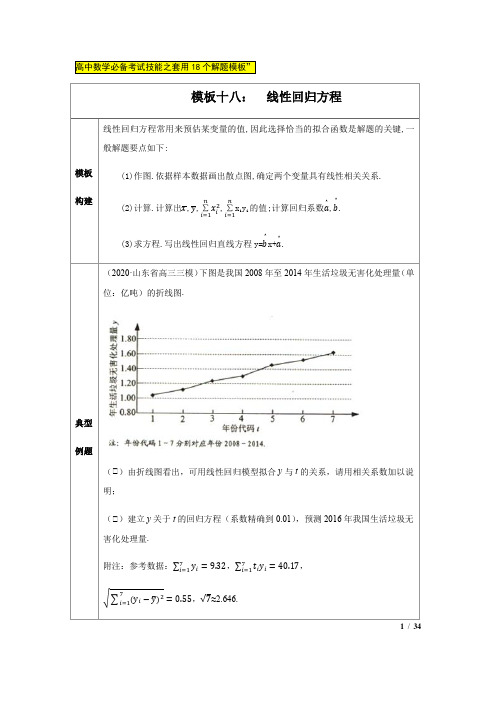
1 / 34（2020·山东省高三三模）下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.（Ⅰ）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明；（Ⅰ）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.附注：参考数据：∑y i 7i=1=9.32，∑t i y i 7i=1=40.17，√∑(y i −y ̅)27i=1=0.55，√7≈2.646.2/ 344 / 34（2）计算相关系数r ，并通过r 的大小说明y 与x 之间的相关程度；（3）求y 与x 的线性回归方程y bx a =+$$$，并推测当产量为3.2万件时销售额为多少.（该问中运算结果保留两位小数）附：回归直线方程y bx a =+$$$中的斜率和截距的最小二乘估计公式分别为()()()121niii nii x x y y bx x ==--=-∑∑$，a y bx =-$$；相关系数()()()()12211niii nniii i x x yyr x x y y ===--=-⋅-∑∑∑.参考数据：10221100.85ii xx =-≈∑，1022110 1.04ii yy -=-≈∑， 1.22b ≈$.3．（2020·安徽省高三三模）随着网购人数的日益增多，网上的支付方式也呈现一种多样化的状态，越来越多的便捷移动支付方式受到了人们的青睐，更被网友们评为“新四大发明”之一.随着人们消费观念的进步，许多人喜欢用信用卡购物，考虑到这一点，一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式，简单便捷，同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系，某网站对其注册用户开展抽样调查，在每个年龄段的注册用户中各随机抽取100人，得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.（1）由大数据可知，在18到44岁之间使用花呗“赊购”的人数百分比y 与年龄x 成线性相关关系，利用统计图表中的数据，以各年龄段的区间中点代表该年龄段的年龄，求所调查群体各年龄段“赊购”人数百分比y 与年龄x 的线性回归方程（回归直线方程的斜率和截距5/ 346 / 345．（2020·湖南省高三二模）2020年全球爆发新冠肺炎，人感染了新冠肺炎病毒后常见的呼吸道症状有：发热、咳嗽、气促和呼吸困难等，严重时会危及生命．随着疫情的发展，自2020年2月5日起，武汉大面积的爆发新冠肺炎，政府为了及时收治轻症感染的群众，逐步建立起了14家方舱医院，其中武汉体育中心方舱医院从2月12日开舱至3月8日闭仓，累计收治轻症患者1056人．据部分统计该方舱医院从2月26日至3月2日轻症患者治愈出仓人数的频数表与散点图如下：日期 2.26 2.27 2.28 2.29 3.1 3.2序号x1 2 3 4 5 6出仓人数y3 8 17 31 68 168根据散点图和表中数据，某研究人员对出仓人数y 与日期序号x 进行了拟合分析．从散点图观察可得，研究人员分别用两种函数Ⅰ2ˆymx p =+Ⅰtxy ke =分析其拟合效果．其相关指数R 2可以判断拟合效果，R 2越大拟合效果越好．已知2y mx p =+的相关指数为20.89R =．（1）试根据相关指数判断．上述两类函数，哪一类函数的拟合效果更好？（注：相关系数r 与相关指数R 2满足22R r =，参考数据表中2ln ,u y v x ==）（2）Ⅰ根据（1）中结论，求拟合效果更好的函数解析式；（结果保留小数点后三位）7 / 34Ⅰ3月3日实际总出仓人数为216人，按Ⅰ中的回归模型计算，差距有多少人？（附：对于一组数据(1,,,))(2,i i x y i n =⋅⋅⋅，其回归直线为ˆˆˆybx a =+ 相关系数()()()()()()()11222111ˆˆ,,,ˆnniiiii i n nni iii i i x x yy x x yy r by bx x x x y a x y=====----===---⋅-∑∑∑∑∑参考数据：xyv u(61ii v=∑2)v -1(bi i y =-∑2)y(61ii u=∑2)u -()()61iii x u u x =--∑ ()()61iii v yy v =--∑3.549.1715.173.13894.8319666.8310.55 13.56 395708317.5 4.18≈，10.55 3.25≈，0.418 1.520e ≈， 5.425227e ≈．6．（2020·陕西省西安中学高三三模）近期，西安公交公司分别推出支付宝和微信扫码支付乘车活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次，x 表示活动推出的天数，y 表示每天使用扫码支付的人次（单位：十人次），统计数据如表下所示：根据以上数据，绘制了散点图.8 / 34（1）根据散点图判断，在推广期内，y a bx =+与xy c d =⋅（,c d 均为大于零的常数），哪一个适宜作为扫码支付的人次y 关于活动推出天数x 的回归方程类型？（给出判断即可，不必说明理由）；（2）根据（1）的判断结果及表1中的数据，建立y 与x 的回归方程，并预测活动推出第8天使用扫码支付的人次；（3）推广期结束后，车队对乘客的支付方式进行统计，结果如下表：西安公交六公司车队为缓解周边居民出行压力，以80万元的单价购进了一批新车，根据以往的经验可知，每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元，使用现金支付的乘客无优惠，使用乘车卡支付的乘客享受8折优惠，扫码支付的乘客随机优惠，根据统计结果得知，使用扫码支付的乘客中有16的概率享受7折优惠，有13的概率享受8折优惠，有12的概率享受9折优惠.预计该车队每辆车每个月有1万人次乘车，根据所给数据以事件发生的频率作为相应事件发生的概率，在不考虑其它因素的条件下，按照上述收费标准，假设这批车需要n （n ∈+N ）年才能开始盈利，求n 的值. 参考数据：9 / 34yv71i ii x y=∑71i ii x v=∑0.541062.14 1.54 2535 50.12 3.47其中其中lg i i v y =，7117i i v v ==∑，参考公式：对于一组数据11(,)u v ，22(,)u v ，L ，(,)n n u v ，其回归直线ˆˆv u αβ=+的斜率和截距的最小二乘估计公式分别为：1221ˆni i i nii u v nu vunu β==-⋅=-∑∑，ˆˆv u αβ=-. 7．（2020·河北省正定中学高三二模）某企业为确定下一年度投入某种产品的生产所需的资金，需了解每投入2千万资金后，工人人数x (单位:百人．．)对年产能y (单位：千万元)的影响，对投入的人力和年产能的数据作了初步处理，得到散点图和统计量表.xy ln y1x21()ni i x x =-∑ 2111()ni ix x =-∑ 1()()n i i i x x y y =--∑ 111()(ln ln )ni i i y y x x =--∑ 1()(ln ln )ni i i x x y y =--∑5.825 3.612 0.154- 1.07732827.87 150.80 55.74- 126.56（1）根据散点图判断:ln y a b x =+与e ba x y +=哪一个适宜作为年产能y 关于投入的人力10 / 34x 的回归方程类型？并说明理由？（2）根据（1）的判断结果及相关的计算数据，建立y 关于x 的回归方程；（3）现该企业共有2000名生产工人，资金非常充足，为了使得年产能达到最大值，则下一年度共需投入多少资金（单位：千万元）？附注：对于一组数据11(,)s t ，22(,)s t ，…，(,)n n s t ，其回归直线t bs a =+的斜率和截距的最小二乘估计分别为$121()(),()niii nii s s tt ba t bs s s ==--==--∑∑$$，(说明:()e ba x f x +=的导函数为2e()b a xb f x x +-⋅'=)8．（2020·湖南省长郡中学高三三模）某企业积极响应国家“科技创新”的号召，大力研发新产品，为了对新研发的一批产品进行合理定价将该产品按事先拟定的价格进行试销，得到一组销售数据(),(1,2,3,4,5,6)i i x y i = 如下表所示：（1）求P 的值；（2）已知变量,x y 具有线性相关关系，求产品销量y （件）关于试销单价x （百元）的线性回归方程（计算结果精确到整数位）（3）用µi y 表示用正确的线性回归方程得到的与i x 对应的产品销量的估计值，当销量数据(),i i x y 的残差的绝对值$1i i y y -<时，则将销售数据称为一个“有效数据”现从这6组数据中任取2组，求抽出的2组销售数据都是“有效数据”的概率附参考公式：6662111180,1606,916i i i i i i i y y x y x =======∑∑∑，11 / 3466116622211()()()iiiii i iii i x x y y x ynx y bx x xnx====---==--∑∑∑∑$，a y bx =-9．（2020·湖南省长郡中学高三三模）为提供市民的健身素质，某市把,,,A B C D 四个篮球馆全部转为免费民用（1）在一次全民健身活动中，四个篮球馆的使用场数如图，用分层抽样的方法从,,,A B C D 四场馆的使用场数中依次抽取1234,,,a a a a 共25场，在1234,,,a a a a 中随机取两数，求这两数和ξ的分布列和数学期望；（2）设四个篮球馆一个月内各馆使用次数之和为x ，其相应维修费用为y 元，根据统计，得到如下表的数据：x 10 15 20 25 30 35 40y 10000 11761 13010 13980 14771 15440 16043430.12yz e=+2.993.494.05 4.50 4.995.49 5.9Ⅰ用最小二乘法求z 与x 的回归直线方程；12/ 3413 / 34（2020·山东省高三三模）下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.（Ⅰ）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明；（Ⅰ）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.附注：参考数据：∑y i 7i=1=9.32，∑t i y i 7i=1=40.17，√∑(y i −y ̅)27i=1=0.55，√7≈2.646.14 / 34（Ⅰ）由折线图中数据和附注中参考数据得t =4，∑(t i −t )27i=1=28，√∑(y i −y ̅)27i=1=0.55，，.因为与的相关系数近似为0.99，说明与的线性相关相当高，从而可以用线性回归模型拟合与的关系. （Ⅰ）由y ̅=9.327≈1.331及（Ⅰ）得b̂=∑(t i −t )(y i −y ̅)7i=1∑(t i −t )27i=1=2.8928≈0.103，a ̂=y ̅−b ̂t ≈1.331−0.103×4≈0.92. 所以，关于的回归方程为：.将2016年对应的代入回归方程得：.所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.15/ 3417/ 3418/ 34（1）由大数据可知，在18到44岁之间使用花呗“赊购”的人数百分比y 与年龄x 成线性相关关系，利用统计图表中的数据，以各年龄段的区间中点代表该年龄段的年龄，求所调查群体各年龄段“赊购”人数百分比y 与年龄x 的线性回归方程（回归直线方程的斜率和截距保留两位有效数字）；（2）该网站年龄为20岁的注册用户共有2000人，试估算该网站20岁的注册用户中使用花呗“赊购”的人数；（3）已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同，现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人，再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度，求抽取的两人年龄都在18到26岁的概率.参考答案：1221ni ii nii x y nx ybxnx==-⋅=-∑∑$，a y bx =-$$.【答案】（1）0.023 1.0y x =-+；（2）1080人；（3）514. 【解析】（1）由题意，223140313x ++==，0.50.30.0822375y ++==，所以222222220.5310.3400.08331 3.78750.023223140331162b ⨯+⨯+⨯-⨯⨯-==≈-++-⨯$，$22 3.7831 1.075162a=+⨯≈，所求线性回归方程为0.023 1.0y x =-+. （2）由（1）知，该网站20岁的注册用户中使用花呗“赊购”的人数百分比为0.02320 1.00.54-⨯+=，而20000.541080⨯=，20/ 3421/ 3422 / 34根据散点图和表中数据，某研究人员对出仓人数y 与日期序号x 进行了拟合分析．从散点图观察可得，研究人员分别用两种函数Ⅰ2ˆymx p =+Ⅰtxy ke =分析其拟合效果．其相关指数R 2可以判断拟合效果，R 2越大拟合效果越好．已知2y mx p =+的相关指数为20.89R =．（1）试根据相关指数判断．上述两类函数，哪一类函数的拟合效果更好？（注：相关系数r 与相关指数R 2满足22R r =，参考数据表中2ln ,u y v x ==）（2）Ⅰ根据（1）中结论，求拟合效果更好的函数解析式；（结果保留小数点后三位） Ⅰ3月3日实际总出仓人数为216人，按Ⅰ中的回归模型计算，差距有多少人？（附：对于一组数据(1,,,))(2,i i x y i n =⋅⋅⋅，其回归直线为ˆˆˆybx a =+ 相关系数()()()()()()()11222111ˆˆ,,,ˆnniiiii i n nni iii i i x x yy x x yy r by bx x x x y a x y=====----===---⋅-∑∑∑∑∑参考数据：xyv u(61ii v=∑ 2)v -1(bii y =-∑(61ii u=∑2)u -()()61iii x u u x =--∑ ()()61iii v yy v =--∑23/ 34即回归方程为0.7750.4180.7751.520x x y ee +==．Ⅰ当序号7x =时，0.7757 5.4251.520 1.520 1.520227345y e e ⨯==⨯=⨯≈， 而3月3日实际出仓人数为216人，相差129人．6．（2020·陕西省西安中学高三三模）近期，西安公交公司分别推出支付宝和微信扫码支付乘车活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次，x 表示活动推出的天数，y 表示每天使用扫码支付的人次（单位：十人次），统计数据如表下所示：根据以上数据，绘制了散点图.（1）根据散点图判断，在推广期内，y a bx =+与xy c d =⋅（,c d 均为大于零的常数），哪一个适宜作为扫码支付的人次y 关于活动推出天数x 的回归方程类型？（给出判断即可，不必说明理由）；（2）根据（1）的判断结果及表1中的数据，建立y 与x 的回归方程，并预测活动推出第8天使用扫码支付的人次；（3）推广期结束后，车队对乘客的支付方式进行统计，结果如下表：西安公交六公司车队为缓解周边居民出行压力，以80万元的单价购进了一批新车，根据以往的经验可知，每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元，使用现金支付的乘客无优惠，使用乘车卡支付的乘客享受8折优惠，扫码支付的乘客随机优惠，根据统计结果得知，使用扫码支付的乘客中有16的概率享受7折优惠，有13的概率享受8折优惠，有12的概率享受9折优惠.预计该车队每辆车每个月有1万人次乘车，根据所给数据以事件发生的频率作为相应事件发生的概率，在不考虑其它因素的条件下，按照上述收费标准，假设这批车需要n （n ∈+N ）年才能开始盈利，求n 的值. 参考数据：yv71i ii x y=∑71i ii x v=∑0.541062.14 1.54 2535 50.12 3.47其中其中lg i i v y =，7117i i v v ==∑，参考公式：对于一组数据11(,)u v ，22(,)u v ，L ，(,)n n u v ，其回归直线ˆˆv u αβ=+的斜率和截距的最小二乘估计公式分别为：1221ˆni i i nii u v nu vunu β==-⋅=-∑∑，ˆˆv u αβ=-. 【答案】（1）x y c d =⋅（2）0.540.250.25103.4710xx y +⋅==⨯，3470（3）7【解析】（1）根据散点图判断，在推广期内， xy c d =⋅（,c d 均为大于零的常数），适宜作为扫码支付的人次y 关于活动推出天数x 的回归方程类型.27 / 34则1.66121800.6612n n ⨯⨯⨯≥+⨯⨯，解得203n ≥。

（2020·山东省高三三模）下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.（Ⅰ）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； （Ⅰ）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.附注：参考数据：∑y i 7i=1=9.32，∑t i y i 7i=1=40.17，√∑(y i −y ̅)27i=1=0.55，√7≈2.646. 参考公式：相关系数r =∑(t i −t )(y i −y ̅)ni=1√∑(t i −t )2∑(y i −¯)2ni=1n i=1，（Ⅰ）由折线图中数据和附注中参考数据得t =4，∑(t i −t )27i=1=28，√∑(y i −y ̅)27i=1=0.55，，.因为与的相关系数近似为0.99，说明与的线性相关相当高，从而可以用线性回归模型拟合与的关系.（Ⅰ）由y ̅=9.327≈1.331及（Ⅰ）得b̂=∑(t i −t )(y i −y ̅)7i=1∑(t i −t )27i=1=2.8928≈0.103，a ̂=y ̅−b ̂t ≈1.331−0.103×4≈0.92. 所以，关于的回归方程为：.将2016年对应的代入回归方程得：.所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.y bt a =+的斜率和截距的最小二乘估计()()()121niii nii t t y y b a y bt t t ==--==--∑∑， 【答案】（1）0.25；（2）Ⅰ理由见解析，不能利用线性回归模型描述∑b=a yb t=-=0.21+0.86所以所求回归直线方程y bx a=+，并推测当产量为y bx a=+中的斜率和截距的最小二乘估计公式分别为((11iinix b== =∑∑a y bx=-；相关系数((11niiniix rx===-∑∑参考数据：1021iix=-∑ 1.22b≈.；具有很强的相关性（3 1.22y x=+4.731a y bx=≈--所以所求回归直线方程为 1.22 1.75y x =+，故当 3.2x =时， 1.22 3.2 1.75 5.65y =⨯+≈.3．（2020·安徽省高三三模）随着网购人数的日益增多，网上的支付方式也呈现一种多样化的状态，越来越多的便捷移动支付方式受到了人们的青睐，更被网友们评为“新四大发明”之一.随着人们消费观念的进步，许多人喜欢用信用卡购物，考虑到这一点，一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式，简单便捷，同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系，某网站对其注册用户开展抽样调查，在每个年龄段的注册用户中各随机抽取100人，得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.（1）由大数据可知，在18到44岁之间使用花呗“赊购”的人数百分比y 与年龄x 成线性相关关系，利用统计图表中的数据，以各年龄段的区间中点代表该年龄段的年龄，求所调查群体各年龄段“赊购”人数百分比y 与年龄x 的线性回归方程（回归直线方程的斜率和截距保留两位有效数字）；（2）该网站年龄为20岁的注册用户共有2000人，试估算该网站20岁的注册用户中使用花呗“赊购”的人数； （3）已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同，现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人，再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度，求抽取的两人年龄都在18到26岁的概率.参考答案：1221ni ii nii x y nx yb xnx==-⋅=-∑∑，a y bx =-.【答案】（1）0.023 1.0y x =-+；（2）1080人；（3）514.220.5b ⨯=22 3.7875162+⨯）由（1）知，该网站20000.541080⨯=y bx a =+；之间是正相关还是负相关，用所求回归方程预测该店营业y bx a =+中，121ni ii nii x y nx b xnx==-=-∑∑bx .11920=.1521i ii ii x y b x===∑∑750.67bx =-所以回归直线方程为0.67b =>之间是正相关.代入回归方程可预测该店营业湖南省高三二模）热、咳嗽、气促和呼吸困难等，严重时会危及生命．随着疫情的发展，自出仓人数y3 8 17 31 68 168根据散点图和表中数据，某研究人员对出仓人数y 与日期序号x 进行了拟合分析．从散点图观察可得，研究人员分别用两种函数Ⅰ2ˆymx p =+Ⅰtx y ke =分析其拟合效果．其相关指数R 2可以判断拟合效果，R 2越大拟合效果越好．已知2y mx p =+的相关指数为20.89R =．（1）试根据相关指数判断．上述两类函数，哪一类函数的拟合效果更好？（注：相关系数r 与相关指数R 2满足22R r =，参考数据表中2ln ,u y v x ==）（2）Ⅰ根据（1）中结论，求拟合效果更好的函数解析式；（结果保留小数点后三位） Ⅰ3月3日实际总出仓人数为216人，按Ⅰ中的回归模型计算，差距有多少人？（附：对于一组数据(1,,,))(2,i i x y i n =⋅⋅⋅，其回归直线为ˆˆˆy bx a =+相关系数()()()()()()()11222111ˆˆ,,,ˆnniiiii i nnnii i i i i x x yy x x yy r by bx x x x y a x y =====----===---⋅-∑∑∑∑∑参考数据：xyv u(61ii v =∑ 1(b ii y =-∑ (61ii u =∑()()61i i i x u u x =--∑ ()()61i ii v yy v =--∑Ⅰi t b ===∑ˆˆb a u ===0.775x =+Ⅰ当序号7x =时，0.7757 5.4251.520 1.520 1.520227345y e e ⨯==⨯=⨯≈， 而3月3日实际出仓人数为216人，相差129人．6．（2020·陕西省西安中学高三三模）近期，西安公交公司分别推出支付宝和微信扫码支付乘车活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次，x 表示活动推出的天数，y 表示每天使用扫码支付的人次（单位：十人次），统计数据如表下所示：根据以上数据，绘制了散点图.（1）根据散点图判断，在推广期内，y a bx =+与x y c d =⋅（,c d 均为大于零的常数），哪一个适宜作为扫码支付的人次y 关于活动推出天数x 的回归方程类型？（给出判断即可，不必说明理由）；（2）根据（1）的判断结果及表1中的数据，建立y 与x 的回归方程，并预测活动推出第8天使用扫码支付的人次；（3）推广期结束后，车队对乘客的支付方式进行统计，结果如下表：西安公交六公司车队为缓解周边居民出行压力，以80万元的单价购进了一批新车，根据以往的经验可知，每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元，使用现金支付的乘客无优惠，使用，，作了初步处理，得到散点图和统计量表.x yln y1x21()ni i x x =-∑ 2111()ni i x x=-∑ 1()()ni i i x x y y =--∑ 111()(ln ln )ni i i y y x x=--∑ 1()(ln ln )niii x x y y =--∑5.825 3.612 0.154- 1.077 328 27.87 150.80 55.74- 126.56（1）根据散点图判断:ln y a b x =+与e ba x y +=哪一个适宜作为年产能y 关于投入的人力x 的回归方程类型？并说明理由？（2）根据（1）的判断结果及相关的计算数据，建立y 关于x 的回归方程；（3）现该企业共有2000名生产工人，资金非常充足，为了使得年产能达到最大值，则下一年度共需投入多少资金（单位：千万元）？附注：对于一组数据11(,)s t ，22(,)s t ，…，(,)n n s t ，其回归直线t bs a =+的斜率和截距的最小二乘估计分别为121()(),()niii nii s s tt b a t bs s s ==--==--∑∑，(说明:()eb axf x +=的导函数为2e()b a xb f x x +-⋅'=)【答案】（1）选择ebaxy +=，理由见解析；（2）22ex y -+=；（3）20千万【解析】（1）由图可知e ba x y +=适宜作为年产能y 关于投入的人力x 的回归方程类型 若选择ln y ab x =+，则0b >，此时当x 接近于0时，y 必小于0，02<<x∴∈(0,2) x∴当x=8．（2020·湖南省长郡中学高三三模）某企业积极响应国家“科技创新”的号召，大力研发新产品，为了对新研发的一批产品进行合理定价将该产品按事先拟定的价格进行试销，得到一组销售数据(),(1,2,3,4,5,6)i i x y i = 如下表所示：（1）求P 的值；（2）已知变量,x y 具有线性相关关系，求产品销量y （件）关于试销单价x （百元）的线性回归方程（计算结果精确到整数位）（3）用i y 表示用正确的线性回归方程得到的与i x 对应的产品销量的估计值，当销量数据(),i i x y 的残差的绝对值1i i y y -<时，则将销售数据称为一个“有效数据”现从这6组数据中任取2组，求抽出的2组销售数据都是“有效数据”的概率附参考公式：6662111180,1606,916i i i i i i i y y x y x =======∑∑∑，66116622211()()()iii ii i iii i x x y y x y nx yb x x xnx====---==--∑∑∑∑，a y bx =-【答案】（1）82p =（2）495y x =-+或494y x =-+（3）25【解析】（1）由611806i i y y ===∑得9186787370806p +++++=. 求得82p =.（2） 3.5x =，6662111180,1606,916i i i i i i i y y x y x =======∑∑∑216066 3.580-744916 3.517.5b -⨯⨯∴==≈--⨯，804 3.594a =+⨯=（或7480 3.595175a ⎛⎫=--⨯≈ ⎪⎝⎭）所以回归方程为495y x =-+或494y x =-+.（3）当11ˆ1,90x y ==，当22ˆ2,86x y ==，当33ˆ3,82x y ==,当44x =，4ˆ78y =;当55x =，5ˆ74y=；当66x =，6ˆ70y=，根据题意则“有效数据”有()()()()2,86,3,82,4,78,6,704个,从6组销售数据中任意抽取2组的所有可能结果有2615C =种，抽取的2组销售数据都是“有效数据”的有246C =种,所以抽取的2组销售数据都是“有效数据”的概率为62155=. 9．（2020·湖南省长郡中学高三三模）为提供市民的健身素质，某市把,,,A B C D 四个篮球馆全部转为免费民用（1）在一次全民健身活动中，四个篮球馆的使用场数如图，用分层抽样的方法从,,,A B C D 四场馆的使用场数中依次抽取1234,,,a a a a 共25场，在1234,,,a a a a 中随机取两数，求这两数和ξ的分布列和数学期望；（2）设四个篮球馆一个月内各馆使用次数之和为x ，其相应维修费用为y 元，根据统计，得到如下表的数据：x 10 15 20 25 30 35 40y 10000 11761 13010 13980 14771 15440 1602043430.12yz e=+2.993.494.05 4.50 4.995.49 5.99Ⅰ用最小二乘法求z 与x 的回归直线方程； Ⅰ40yx +叫做篮球馆月惠值，根据Ⅰ的结论，试估计这四个篮球馆月惠值最大时x 的值 参考数据和公式：7723114.5,()700,()()70,20ii i i i z x x x x z z e ===-=--==∑∑71721()()()iii ii x x zz b x x ==--=-∑∑，a z bx =-【答案】（1）见解析，12.5（2）Ⅰ0.12z x =+Ⅰ20【解析】（1）抽样比为2511004=，所以1234,,,a a a a 分别是，6，7，8，5 所以两数之和所有可能取值是：10，12，13，15()1106p ξ==，()1123p ξ==，()1133p ξ==，()1156p ξ==所以分布列为期望为1111()1012131512.56336E ξ=⨯+⨯+⨯+⨯= （2）因为77211()700,()()70,ii i i i x x x x z z ==-=--=∑∑所以71721()()()iii ii x x zz b x x ==--=-∑∑，701, 4.50.125270010a ===-⨯=， 0.12z x ∴=+；y bx a =+月初购入进口猪肉，如果猪肉单价超过量以调控猪肉价格，试判断自受影响后第几周开始需要释放进口猪肉？·ni ix y nx y -∑2.56y x =12x ++=22345+++2.56y x =2）当6x =28.68y =，当31.24y =，所以应从第7周开始释放进口猪肉。

线性回归公式
线性回归方程公式：b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。

线性回归方程是利用数理统计中的回归分析，来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一，应用十分广泛。

线性回归方程中变量的相关关系最为简单的是线性相关关系，设随机变量与变量之间存在线性相关关系，则由试验数据得到的点，将散布在某一直线周围。

因此，可以认为关于的回归函数的类型为线性函数。

分析按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

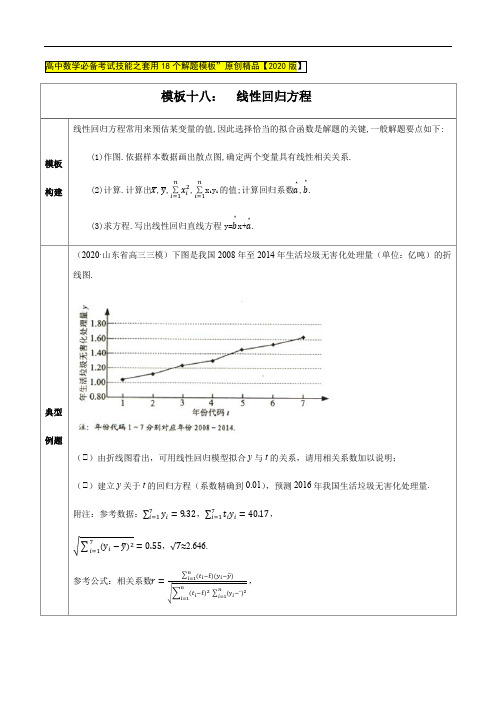
（2020·山东省高三三模）下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.（Ⅰ）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； （Ⅰ）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.附注：参考数据：∑y i 7i=1=9.32，∑t i y i 7i=1=40.17，√∑(y i −y ̅)27i=1=0.55，√7≈2.646. 参考公式：相关系数r =∑(t i −t )(y i −y ̅)ni=1√∑(t i −t )2∑(y i −¯)2ni=1n i=1，（Ⅰ）由折线图中数据和附注中参考数据得t =4，∑(t i −t )27i=1=28，√∑(y i −y ̅)27i=1=0.55，，.因为与的相关系数近似为0.99，说明与的线性相关相当高，从而可以用线性回归模型拟合与的关系.（Ⅰ）由y ̅=9.327≈1.331及（Ⅰ）得b̂=∑(t i −t )(y i −y ̅)7i=1∑(t i −t )27i=1=2.8928≈0.103，a ̂=y ̅−b ̂t ≈1.331−0.103×4≈0.92. 所以，关于的回归方程为：.将2016年对应的代入回归方程得：.所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.故当 3.2x =时， 1.22 3.2 1.75 5.65y =⨯+≈$.3．（2020·安徽省高三三模）随着网购人数的日益增多，网上的支付方式也呈现一种多样化的状态，越来越多的便捷移动支付方式受到了人们的青睐，更被网友们评为“新四大发明”之一.随着人们消费观念的进步，许多人喜欢用信用卡购物，考虑到这一点，一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式，简单便捷，同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系，某网站对其注册用户开展抽样调查，在每个年龄段的注册用户中各随机抽取100人，得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.（1）由大数据可知，在18到44岁之间使用花呗“赊购”的人数百分比y 与年龄x 成线性相关关系，利用统计图表中的数据，以各年龄段的区间中点代表该年龄段的年龄，求所调查群体各年龄段“赊购”人数百分比y 与年龄x 的线性回归方程（回归直线方程的斜率和截距保留两位有效数字）；（2）该网站年龄为20岁的注册用户共有2000人，试估算该网站20岁的注册用户中使用花呗“赊购”的人数； （3）已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同，现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人，再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度，求抽取的两人年龄都在18到26岁的概率.参考答案：1221ni ii nii x y nx ybxnx==-⋅=-∑∑$，a y bx =-$$.【答案】（1）0.023 1.0y x =-+；（2）1080人；（3）514. 【解析】（1）由题意，223140313x ++==，0.50.30.0822375y ++==，根据散点图和表中数据，某研究人员对出仓人数y 与日期序号x 进行了拟合分析．从散点图观察可得，研究人员分别用两种函数Ⅰ2ˆymx p =+Ⅰtxy ke =分析其拟合效果．其相关指数R 2可以判断拟合效果，R 2越大拟合效果越好．已知2y mx p =+的相关指数为20.89R =．（1）试根据相关指数判断．上述两类函数，哪一类函数的拟合效果更好？（注：相关系数r 与相关指数R 2满足22R r =，参考数据表中2ln ,u y v x ==）（2）Ⅰ根据（1）中结论，求拟合效果更好的函数解析式；（结果保留小数点后三位） Ⅰ3月3日实际总出仓人数为216人，按Ⅰ中的回归模型计算，差距有多少人？（附：对于一组数据(1,,,))(2,i i x y i n =⋅⋅⋅，其回归直线为ˆˆˆybx a =+ 相关系数()()()()()()()11222111ˆˆ,,,ˆnniiiii i n nni iii i i x x yy x x yy r by bx x x x y a x y=====----===---⋅-∑∑∑∑∑参考数据：xy v u(61ii v=∑2)v -1(b ii y =-∑2)y(61ii u=∑2)u -()()61iii x u u x =--∑ ()()61iii v yy v =--∑6．（2020·陕西省西安中学高三三模）近期，西安公交公司分别推出支付宝和微信扫码支付乘车活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次，x 表示活动推出的天数，y 表示每天使用扫码支付的人次（单位：十人次），统计数据如表下所示：根据以上数据，绘制了散点图.（1）根据散点图判断，在推广期内，y a bx =+与xy c d =⋅（,c d 均为大于零的常数），哪一个适宜作为扫码支付的人次y 关于活动推出天数x 的回归方程类型？（给出判断即可，不必说明理由）；（2）根据（1）的判断结果及表1中的数据，建立y 与x 的回归方程，并预测活动推出第8天使用扫码支付的人次；（3）推广期结束后，车队对乘客的支付方式进行统计，结果如下表：西安公交六公司车队为缓解周边居民出行压力，以80万元的单价购进了一批新车，根据以往的经验可知，每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元，使用现金支付的乘客无优惠，使用乘车卡支付的乘客享受8折优惠，扫码支付的乘客随机优惠，根据统计结果得知，使用扫码支付的乘客中有16的概率享受7折优惠，有13的概率享受8折优惠，有12的概率享受9折优惠.预计该车队每辆车每个月有1万人次乘车，根据所给数据以事件发生的频率作为相应事件发生的概率，在不考虑其它因素的条件下，按5.825 3.612 0.154- 1.07732827.87 150.80 55.74- 126.56（1）根据散点图判断:ln y a b x =+与e ba x y +=哪一个适宜作为年产能y 关于投入的人力x 的回归方程类型？并说明理由？（2）根据（1）的判断结果及相关的计算数据，建立y 关于x 的回归方程；（3）现该企业共有2000名生产工人，资金非常充足，为了使得年产能达到最大值，则下一年度共需投入多少资金（单位：千万元）？附注：对于一组数据11(,)s t ，22(,)s t ，…，(,)n n s t ，其回归直线t bs a =+的斜率和截距的最小二乘估计分别为$121()(),()niii nii s s tt ba t bs s s ==--==--∑∑$$，(说明:()eba xf x +=的导函数为2e()b a xb f x x+-⋅'=)【答案】（1）选择e b a x y +=，理由见解析；（2）22e x y -+=；（3）20千万 【解析】（1）由图可知eba xy +=适宜作为年产能y 关于投入的人力x 的回归方程类型Q 若选择ln y a b x =+，则0b >，此时当x 接近于0时，y 必小于0，故选择e ba x y +=作为年产能y 关于投入的人力x 的回归方程类型(),(1,2,3,4,5,6)i i x y i = 如下表所示：（1）求P 的值；（2）已知变量,x y 具有线性相关关系，求产品销量y （件）关于试销单价x （百元）的线性回归方程（计算结果精确到整数位）（3）用µi y 表示用正确的线性回归方程得到的与i x 对应的产品销量的估计值，当销量数据(),i i x y 的残差的绝对值$1i i y y -<时，则将销售数据称为一个“有效数据”现从这6组数据中任取2组，求抽出的2组销售数据都是“有效数据”的概率附参考公式：6662111180,1606,916i i i i i i i y y x y x =======∑∑∑，66116622211()()()iiiii i iii i x x y y x ynx y b x x xnx====---==--∑∑∑∑$，a y bx =-【答案】（1）82p =（2）495y x =-+或494y x =-+（3）25【解析】（1）由611806i i y y ===∑得9186787370806p +++++=. 求得82p =.（2） 3.5x =Q ，6662111180,1606,916i i i i i i i y y x y x =======∑∑∑216066 3.580-744916 3.517.5b-⨯⨯∴==≈--⨯$，$804 3.594a =+⨯=（或$7480 3.595175a ⎛⎫=--⨯≈ ⎪⎝⎭） 所以回归方程为495y x =-+或494y x =-+.（3）当11ˆ1,90x y==，当22ˆ2,86x y ==，当33ˆ3,82x y ==,当44x =，4ˆ78y =;当55x =，5ˆ74y =；当66x =，6ˆ70y=，根据题意则“有效数据”有()()()()2,86,3,82,4,78,6,704个,从6组销售数据中任意抽取2组的所有可能结果有2615C =种，抽取的2组销售数据都是“有效数据”的有246C =种,所以抽取的2组销售数据都是“有效数据”的概率为62155=. 9．（2020·湖南省长郡中学高三三模）为提供市民的健身素质，某市把,,,A B C D 四个篮球馆全部转为免费民用（1）在一次全民健身活动中，四个篮球馆的使用场数如图，用分层抽样的方法从,,,A B C D 四场馆的使用场数中依次抽取1234,,,a a a a 共25场，在1234,,,a a a a 中随机取两数，求这两数和ξ的分布列和数学期望；（2）设四个篮球馆一个月内各馆使用次数之和为x ，其相应维修费用为y 元，根据统计，得到如下表的数据：x 10 15 20 25 30 35 40y 10000 11761 13010 13980 14771 15440 1602043430.12yz e=+2.993.494.05 4.50 4.995.49 5.99Ⅰ用最小二乘法求z 与x 的回归直线方程；Ⅰ40yx +叫做篮球馆月惠值，根据Ⅰ的结论，试估计这四个篮球馆月惠值最大时x 的值 参考数据和公式：7723114.5,()700,()()70,20ii i i i z x x x x z z e ===-=--==∑∑71721()()()iii ii x x zz bx x ==--=-∑∑$，$az bx =- 【答案】（1）见解析，12.5（2）Ⅰ0.12z x =+$Ⅰ20【解析】（1）抽样比为2511004=，所以1234,,,a a a a 分别是，6，7，8，5 所以两数之和所有可能取值是：10，12，13，15()1106p ξ==，()1123p ξ==，()1133p ξ==，()1156p ξ== 所以分布列为期望为1111()1012131512.56336E ξ=⨯+⨯+⨯+⨯= （2）因为77211()700,()()70,ii i i i x x x x z z ==-=--=∑∑所以71721()()()iii ii x x zz bx x ==--=-∑∑$，$701, 4.50.125270010a ===-⨯=， 0.12zx ∴=+$； Ⅰ43430.12yz e=+0.12x =+，。

线性回归方程公式_数学公式线性回归方程公式线性回归方程公式：b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。

线性回归方程公式求法：第一：用所给样本求出两个相关变量的(算术)平均值：x_=(x1+x2+x3+...+xn)/ny_=(y1+y2+y3+...+yn)/n第二：分别计算分子和分母：(两个公式任选其一)分子=(x1y1+x2y2+x3y3+...+xnyn)-nx_Y_分母=(x1^2+x2^2+x3^2+...+xn^2)-n__x_^2第三：计算b：b=分子/分母用最小二乘法估计参数b，设服从正态分布，分别求对a、b的偏导数并令它们等于零。

其中，且为观测值的样本方差.线性方程称为关于的线性回归方程，称为回归系数，对应的直线称为回归直线.顺便指出，将来还需用到，其中为观测值的样本方差。

先求x，y的平均值X，Y再用公式代入求解:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)后把x，y的平均数X，Y代入a=Y-bX求出a并代入总的公式y=bx+a得到线性回归方程(X为xi的平均数，Y为yi的平均数)线性回归方程的应用线性回归方程是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。

这是因为线性依赖于其未知参数的模型比非线性依赖于其位置参数的模型更容易拟合，而且产生的估计的统计特性也更容易确定。

线性回归有很多实际用途。

分为以下两大类：如果目标是预测或者映射，线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。

当完成这样一个模型以后，对于一个新增的X值，在没有给定与它相配对的y的情况下，可以用这个拟合过的模型预测出一个y值。

给定一个变量y和一些变量X1,...,Xp，这些变量有可能与y相关，线性回归分析可以用来量化y与Xj之间相关性的强度，评估出与y不相关的Xj，并识别出哪些Xj的子集包含了关于y的冗余信息。