- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
J ω 1 = J ω 2 + mvl .
lmg +
2 J ω 2 = mgh
4. 如图:空心环 :R,初角速度ω0 ,对轴转动惯量为 如图:空心环B: , 小球A:质量为m J0 . 小球 :质量为 . 小球A无摩擦滑到 点时相对于环 无摩擦滑到b,c点时相对于环的速率 求:小球 无摩擦滑到 点时相对于环的速率 .
2.如图 知A: m,l,质量均匀 开始时水平静止 如图,知 质量均匀,开始时水平静止 如图 质量均匀 B:m , , A竖直时被碰 竖直时被碰, 竖直时被碰 m 然后滑行距离S. 然后滑行距离 A l 碰后A的质心可达高度 求 :碰后 的质心可达高度 碰后 的质心可达高度h.
思考:几个过程 各有何特点 思考 几个过程,各有何特点 几个过程 各有何特点? 由水平下摆至垂直, 解:A由水平下摆至垂直,机械能守恒. 由水平下摆至垂直 机械能守恒. 1 2 1 以地面为零势点 mgl = Jω + mgl
ω10 ω20
1
ω1
ω2
AΟ
R1
B
Ο2
R2
AΟ
1
B R2 R1 Ο2
方法如下: 求解它们的角速度ω1和ω2 方法如下 两滑轮边缘线速度相同,所以 两滑轮边缘线速度相同 所以 ω 1 R1 = ω 2 R2 设两滑轮边缘相互作用力大小为F,根据角动量定理 设两滑轮边缘相互作用力大小为 根据角动量定理
(三) 课堂讨论题 1 .当两个力作用在一个有固定转轴的刚体上 当两个力作用在一个有固定转轴的刚体上, 当两个力作用在一个有固定转轴的刚体上 下列说法正确吗? 下列说法正确吗 (1)这两个力都平行于轴作用时它们对轴的合 这两个力都平行于轴作用时它们对轴的合 力矩一定为零; 力矩一定为零 (2)这两个力都垂直于轴作用时它们对轴的 这两个力都垂直于轴作用时它们对轴的 合力矩可能为零; 合力矩可能为零 (3)这两个力矢量和为零时 它们对轴的合力 这两个力矢量和为零时,它们对轴的合力 这两个力矢量和为零时 矩一定为零; 矩一定为零 (4)这两个力对轴的合力矩为零时 它们的 这两个力对轴的合力矩为零时,它们的 这两个力对轴的合力矩为零时 矢量和一定为零; 矢量和一定为零
转动 转动惯量J 转动惯性 转动惯量 质点系 J = ∑ miri2 质量连续分布 J = ∫ r 2 dm 转动定律dL = dtF =源自mab aM = Jβ
W = ∫ Mdθ P = Mω E k = Jω 2 / 2
转动动
2
功 和 能 动
P = dW / dt = Fvcosθ 2 E k = mv / 2
O A a B R b B R
ω0
A a
O
ω
b vbt
c
vc
c
O' O' 分析:问题的性质,系统选择, 分析:问题的性质,系统选择,运动特征 . . .
小球下落过程,球与环组成的系统对轴oo'角动量守恒 解:小球下落过程,球与环组成的系统对轴 角动量守恒 J 0ω 0 2 a→b: J 0 ω 0 = ( J 0 + mR )ω b ω b = J 0 + mR 2 a→c: J 0ω 0 = J 0ω c , ω c = ω 0 O
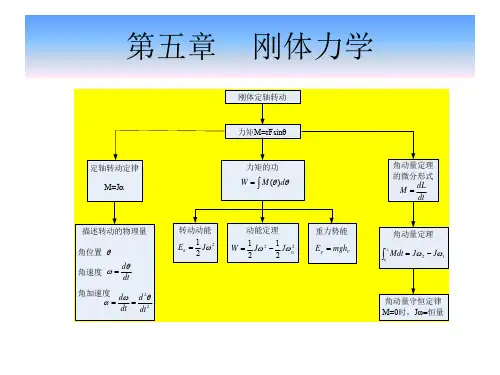
刚体力学 习题课
力学内容总结
平动 转动 关系 位移 r = r2 r1 角位移 θ = θ 2 θ1 ω = dθ / dt 速度 v = dr / dt 角速度 加速度 a = dv / dt 角加速度 β = dω / dt 切向加速度
r = rθ v = rω
an = rω 2
2 a = aτ2 + an
aτ = rβ
运 动 学
aτ = dv / dt
向加速度 速
an = v / r
2
a = r β 2 +ω4
动
v = v0 + at x = v0t + at 2 / 2
ω = ω0 + β t θ = ω0t + β t 2 / 2
速转动
v2 = v0 + 2ax
2
ω = ω0 + 2βθ
2 2
平动 质量m 动 平动惯性 质量 力 学 M = r ×F 牛顿第二定律
2 2
功 和 能
∑ W外 + ∑ W内非 = E E 0
∑ W外 + ∑ W内非 = E E 0
E = ∑ mv 2 / 2 + ∑ mgh + ∑ kx 2 / 2
E = ∑ mv 2 / 2 + ∑ mgh + ∑ kx 2 / 2 + ∑ Jω 2 / 2
E0 = E
E0 = E
平动
转动
ω
4. 质量分别为 1,M2,R1,R2的两个均匀圆柱 质量分别为M 体可分别绕它们本身的轴转动,二轴平行 二轴平行.开始时 体可分别绕它们本身的轴转动 二轴平行 开始时 匀速转动,然后平移 它们分别以角速度ω10 , ω20匀速转动 然后平移 两轴使他们的边缘互相接触.试分析在此过程中 两轴使他们的边缘互相接触 试分析在此过程中 以两圆柱为系统,对O1或O2的角动量是否守恒?如 以两圆柱为系统 对 的角动量是否守恒 如 何求解当两圆柱的接触点无相对滑动时,它们的 何求解当两圆柱的接触点无相对滑动时 它们的 角速度ω1和ω2 ?
错!环不是惯性系 对地面: (2)对地面: 设小球A在 点对地的速率为 的速率为V 设小球 在b点对地的速率为V
3. 一圆盘可绕垂直于盘面 且通过盘心的中心轴OO'以 且通过盘心的中心轴 以 角速度ω沿顺时针方向转动 转动. 角速度ω沿顺时针方向转动
O v v
ω
(1) 在同一水平直线以相反方 Jω = J 0ω 0 O' 向同时射入两颗质量相同, 向同时射入两颗质量相同,速率 J > J 0 ∴ ω < ω 0 相等的子弹,并留在盘中, 相等的子弹,并留在盘中,盘的 盘的角速度减小 因为角 盘的角速度减小,因为角 角速度如何变化? 角速度如何变化? 动量L=J ω不变 但转动惯 不变,但转动惯 动量 加大了. 量J加大了 加大了 (2)两大小相等 两大小相等, (2)两大小相等,方向相反但不在 F 同一直线上的力沿盘面同时作用 在盘上,盘的角速度如何变化? 在盘上,盘的角速度如何变化? 盘的角速度增大,因为转盘受到同向的力矩 盘的角速度增大 因为转盘受到同向的力矩 与 M > M ′ M与ω同方向 ∴ ω > ω 0 O' O F'
a = 2.4 4 x m s
2
的速率 (2)当 a=0;β =0 时, A的速率 v = v max ) dv dv 1 2 2 a= =v ; v = 2.4 x 2x dt dx 2 得 vmax = 1.2 m s (3) 设:A由静止释放沿斜面下滑的最大距离为 S , 由静止释放沿斜面下滑的最大距离为 则以A,B,C为系统,其机械能守恒. 为系统, 则以 为系统 其机械能守恒. 1 2 ks mgssinα = 0 得 s = 1.2 m 2
定
2 2 0
W = ∫ F dr
θ θ0
转动动 定 系动
质点动
定
2 0
W = mv / 2 mv / 2
质点系动 定
W = Jω / 2 Jω / 2
定
∑ W外 + ∑ W内 = E k E k 0
∑ W外 + ∑ W内 = E k E k 0
平动
转动
E k = ∑ mv / 2
2
E k = ∑ mv / 2 + ∑ J ω / 2
t t0
动 动 量 动
∫ F dt P = mv
I=
∫
动 动
t
t0
M dt
L = r×P
L = Jω
∫
t
t0
F dt = m v m v 0
动
∫
t
t0
M dt = L L 0
∫
动
t
P=
t0
F dt = P P0
∑ mv
动 0 0
P0 = P
L0 = L
四大定理, 四大定理,三大守恒
四大定理 1.动能定理 动能定理 2.功能原理 功能原理 3.动量定理 动量定理 4.角动量定理 角动量定理 1.机械能守恒 机械能守恒 三大守恒 2.动量守恒 动量守恒 3.角动量守恒 角动量守恒
1 FR1dt = M 1 R12 (ω 1 ω 10 ) ∫ 2 1 2 FR2dt = M 2 R2 (ω 2 ω 20 ) ∫ 2
ω1 ω2
AΟ B R2 R1 Ο2
1
求解上述方程可得ω1和ω2 .
四 基本能力训练题 (一)填空题 (二)计算题
1.已知 如图,m=2.0kg,0.5R=m,k=20N/m,j=7.5kgm2 , 已知:如图 已知 如图, 不计摩擦.当弹簧无形变时将 由静止释放.求 α=37°.不计摩擦 当弹簧无形变时将A由静止释放 求 ° 不计摩擦 当弹簧无形变时将 由静止释放 B (1)A下滑的加速度 下滑的加速度; 下滑的加速度 R (2)A下滑的最大速率 下滑的最大速率; 下滑的最大速率 (3)A下滑的最大距离 下滑的最大距离; 下滑的最大距离 O A k m 解法1:(1)受力分析如图, 解法1:(1)受力分析如图, 1:(1)受力分析如图 C 取弹簧为原长时物体A位置 取弹簧为原长时物体 位置 α=37° ° x 下滑x 下滑 为原点. 为原点.当A下滑 时,有: T1 C : T2 = kx A m B B : ( T1 T2 )R = Jβ T1 T2 A : mg sinα T1 = ma ; mg α
a = Rβ
联立求解,得 联立求解 得: