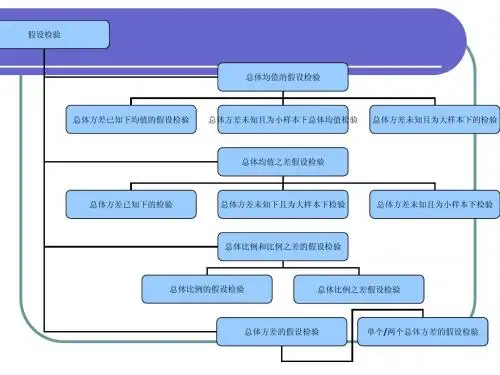
3[1]3总体方差的假设检验
- 格式:doc
- 大小:296.51 KB
- 文档页数:10



假设检验的定义和步骤
假设检验是统计学中一种常用的推断方法,用于判断样本数据
是否支持对总体参数的某个假设。
通过对样本数据进行分析,假设
检验可以帮助我们判断我们所做的假设是否合理,并据此对总体参
数进行推断。
假设检验的步骤通常包括以下几个步骤:
1. 提出假设,首先,我们需要明确提出一个关于总体参数的假设,通常包括原假设(H0)和备择假设(H1)两种。
2. 选择检验统计量,根据所提出的假设,选择适当的检验统计量,该统计量应能够在原假设成立时具有已知的概率分布。
3. 确定显著性水平,确定显著性水平(α),即拒绝原假设的
概率阈值。
通常选择0.05作为显著性水平。
4. 计算统计量的值,利用样本数据计算出所选检验统计量的值。
5. 做出决策,根据检验统计量的值和显著性水平,做出决策,
即是拒绝原假设还是不拒绝原假设。
6. 得出结论,根据做出的决策,得出对原假设的结论,判断样本数据是否支持原假设。
总的来说,假设检验是一种通过对样本数据进行统计分析,以判断对总体参数的假设是否成立的方法。
通过严格的步骤和逻辑推理,假设检验可以帮助我们做出合理的推断和决策。

常⽤的假设检验⽅法(U检验、T检验、卡⽅检验、F检验)⼀、假设检验假设检验是根据⼀定的假设条件,由样本推断总体的⼀种⽅法。
假设检验的基本思想是⼩概率反证法思想,⼩概率思想认为⼩概率事件在⼀次试验中基本上不可能发⽣,在这个⽅法下,我们⾸先对总体作出⼀个假设,这个假设⼤概率会成⽴,如果在⼀次试验中,试验结果和原假设相背离,也就是⼩概率事件竟然发⽣了,那我们就有理由怀疑原假设的真实性,从⽽拒绝这⼀假设。
⼆、假设检验的四种⽅法1、有关平均值参数u的假设检验根据是否已知⽅差,分为两类检验:U检验和T检验。
如果已知⽅差,则使⽤U检验,如果⽅差未知则采取T检验。
2、有关参数⽅差σ2的假设检验F检验是对两个正态分布的⽅差齐性检验,简单来说,就是检验两个分布的⽅差是否相等3、检验两个或多个变量之间是否关联卡⽅检验属于⾮参数检验,主要是⽐较两个及两个以上样本率(构成⽐)以及两个分类变量的关联性分析。
根本思想在于⽐较理论频数和实际频数的吻合程度或者拟合优度问题。
三、U检验(Z检验)U检验⼜称Z检验。
Z检验是⼀般⽤于⼤样本(即⼤于30)平均值差异性检验的⽅法(总体的⽅差已知)。
它是⽤标准的理论来推断差异发⽣的概率,从⽽⽐较两个的差异是否显著。
Z检验步骤:第⼀步:建⽴虚⽆假设 H0:µ1 = µ2 ,即先假定两个平均数之间没有显著差异,第⼆步:计算Z值,对于不同类型的问题选⽤不同的计算⽅法,1、如果检验⼀个样本平均数(X)与⼀个已知的总体平均数(µ0)的差异是否显著。
其Z值计算公式为:其中:X是检验样本的均值;µ0是已知总体的平均数;S是总体的标准差;n是样本容量。
2、如果检验来⾃两个的两组样本平均数的差异性,从⽽判断它们各⾃代表的总体的差异是否显著。
其Z值计算公式为:第三步:⽐较计算所得Z值与理论Z值,推断发⽣的概率,依据Z值与差异显著性关系表作出判断。
如下表所⽰:第四步:根据是以上分析,结合具体情况,作出结论。


统计学三大检验方法引言统计学三大检验方法是指假设检验、置信区间估计和方差分析。
这三种方法是统计学中非常重要的工具,用来对样本数据进行分析和推断。
本文将详细介绍这三种方法的原理、应用和步骤。
一、假设检验假设检验是一种基于样本数据对总体参数进行推断的方法。
它的目的是判断样本数据对某一假设的支持程度。
假设检验的步骤可以分为以下几个部分:1.明确研究问题和假设。
首先确定研究的目的和问题,然后提出关于总体参数的假设,包括原假设和备择假设。
2.选择合适的检验统计量。
根据问题和数据的特点,选择适合的检验统计量,如均值差检验的t统计量、比例差检验的z统计量等。
3.设定显著性水平。
显著性水平是在假设检验中用来判断是否拒绝原假设的标准,通常取0.05或0.01。
4.计算检验统计量的观察值。
根据样本数据计算出具体的检验统计量的观察值。
5.给出结论。
通过计算观察值与临界值的比较,得出对原假设的结论,并解释结果的意义。
二、置信区间估计置信区间估计是一种用来对总体参数进行估计的方法。
它通过样本数据计算出的区间,给出了总体参数的一个估计范围。
1.确定置信水平。
置信水平是在置信区间估计中用来描述区间的可靠程度,通常取0.95。
2.选择适合的估计方法。
根据总体参数的类型和样本数据的特点,选择适合的估计方法,如均值估计的t分布、比例估计的正态分布等。
3.计算置信区间。
根据样本数据和所选的估计方法,计算出具体的置信区间,通常采用公式:估计值±临界值×标准差/√n。
4.解释结果。
解释置信区间的意义,并进行合理的解释和讨论。
三、方差分析方差分析是一种用于比较两个或多个组之间差异的方法。
它是通过分解总体方差,分析组内与组间的差异,来判断组间的差异是否显著。
1.确定研究问题。
确定需要比较的组,并明确研究的目的和问题。
2.设定假设。
设定组间差异的原假设和备择假设。
3.计算方差。
计算组内方差和组间方差。
4.计算F统计量。
根据方差计算出F统计量。




统计学中的方差分析与假设检验方差分析(Analysis of Variance,简称ANOVA)是统计学中一种常用的假设检验方法,用于比较两个或多个样本的均值是否存在显著差异。
方差分析通过对不同组之间的方差进行比较,判断样本均值是否有统计学上的差异。
本文将介绍方差分析的基本原理和假设检验的步骤。
一、方差分析的基本原理方差分析是一种多个总体均值比较的方法,它通过计算组间离散度与组内离散度的比值来判断样本均值是否有显著差异。
方差分析的基本原理可以用以下公式表示:$$F=\frac{MS_{\text{between}}}{MS_{\text{within}}}$$其中,F为方差比值,$MS_{\text{between}}$为组间均方,$MS_{\text{within}}$为组内均方。
方差比值F的值越大,说明组间差异相对于组内差异的贡献越大,即样本均值之间的差异越显著。
通过查找F分布表,可以确定F值对应的显著性水平,从而判断样本均值是否有显著差异。
二、假设检验的步骤方差分析的假设检验可以分为以下几个步骤:1. 建立假设- 零假设(H0):各组样本的均值相等,即$\mu_1=\mu_2=...=\mu_k$- 备择假设(H1):至少有两个组样本的均值不相等,即$\mu_i\neq\mu_j$2. 计算组间均方- 组间均方$MS_{\text{between}}$的计算公式为:$MS_{\text{between}}=\frac{SS_{\text{between}}}{df_{\text{between}}}$ - 其中,$SS_{\text{between}}$为组间平方和,$df_{\text{between}}$为组间自由度。
3. 计算组内均方- 组内均方$MS_{\text{within}}$的计算公式为:$MS_{\text{within}}=\frac{SS_{\text{within}}}{df_{\text{within}}}$ - 其中,$SS_{\text{within}}$为组内平方和,$df_{\text{within}}$为组内自由度。
§3 检验母体方差 3.1 检验正态母体的方差
——2
χ检验
母体),(~2σμN X ,2
,σμ均未知,试对
2
σ与2
0σ有无显著差异作假设检验.
①在母体上作
假设
↔=2
020:σσH 2021:σσ≠H
②检验统计量
)1( ~ )1(22
02
2
--=*n S
n H χσχ
③给定显著水平α,如图存在
)1(22
1--
n α
χ
和)1(2
2
-n αχ,使
2
)}1({)}1({2
2
222
12α
χχχ
χαα
=
->=-<-
n P n P
故取拒绝域
}
)1()1(),,,{(2
2
222
12
21->-<=-
n n x x x W n αα
χχχ
χ或
④决策:当抽样结果是
W
x x x n ∈),,,(21 时,拒绝0
H ,认为2
σ与2
0σ有
显著差异;否则接受0
H ,认为2
σ与20
σ无
显著差异.
例3.3.1 某细纱车间纺出的一种细纱支数的标准差2.10=σ,现从某日纺出的一批细纱中随机抽出16缕进行支数测
量,算得子样标准差1.2*
=s ,问:纱的均
匀度有无显著变化(取05.0=α)?假定
母体分布是正态的。
解: 设该日纺出的纱的支数
),(~2
σμN X ,2
,σμ均未知,
作假设↔=2.1:20σH 2.1:21
≠σH 检验统计量)1(~
)1(22
22
--=
*n S
n H χσ
χ
给定显著水平α,拒绝域为
}
)1()1(),,,{(2
2
222
1221->-<=-n n x x x W n ααχχχχ或
这时16=n ,2.10=σ,1.2*
=s ,从而94.452
=χ,又05.0=α,查表得
262.6)15()1(975.02
1==--
χχ
α
n ,
488.27)15()1(025.02
==-χχαn ,
可见)1(2
2
->n αχχ,故应拒绝0H ,认为
这天细纱的均匀度有显著变化。
例3.3.2
),(~2
σμN X ,
2
,σμ均未知,
当45>n ,作如下假设检验
↔=2
2
0:σσH 2021:σσ≠H
检验统计量取为2
02
2
)1(σχ
*-=
S
n ,证明:给
定显著水平α,则拒绝域为
}
)1(2)1({})1(2)1({2
22
2ααχχu n n u n n W ---≤-+-≥= .
证明:作假设↔=2020:σσH 2
021:σσ≠H ,
0H 成立时检验统计量
)1(~)1(2
20
22
--=
*n S
n H χσ
χ
而45>n ,由2
χ分布的性质知,
)
1,0()
1(2)
1(~
2
N n n U H 近似
---=
χ
给定显著水平α,拒绝域为
}
)
1(2)
1({
}{2
22
ααχu n n u U W ≥---=≥=
}
)1(2)1({})1(2)1({2
22
2ααχχu n n u n n ---≤-+-≥= 证毕.
3.2 检验两个正态母体的方差相等——F 检验
设母体),(~2
11σμN X ,母体),(~2
22σμN Y ,
且X 与Y 相互独立,
2
221σσ,未知,试对21σ与
2
2
σ有无显著差异作假设检验.
①在母体上作假设
↔=22210:σσH 2
2211:σσ≠H
②
检
验
统计量
)
1,1(~ / 212*2*22
212*2*0
--==n n F S
S S S
F H
Y
X H Y
X σσ ③给定显著水平α,如图存在
)1,1(212
1---
n n F α和)1,1(212
--n n F α,使 2
)}1,1({)}1,1({212
212
1α
αα
=
-->=--<-
n n F F P n n F
F P
故取拒绝域
()1,1(),,,;,,,{(1
2
212
1212121>--<=-
n F F n n F
F y y y x x x W n n αα
或
④决策:当抽样结果是W y y y x x x n n ∈),,,;,,,(2
1
2121 时,拒绝0
H ,认
为2
1σ与22σ有显著差异;否则接受0
H ,认为2
1σ与22σ无显著差异.
注①: 在本章检验两个正态母体的均值相等,及在上一章求两个正态母体的均值之差的置信区间时,均须假定两个正态母体的方差相等。
——实际问题中,这一假设是否合理,可以用上述方
法去检验。
例3.3.3 有两种冶金方法,所得产
品中的杂质含量(%)分别为,
),(~2
11σμN X ,),(~2
22σμN Y ,且
X 与Y 相互独立,各抽取
一个子样,杂质含量(%)如下:
问:两种方法生产的产品中所含杂质的波动性有无显著差异(取05.0=α)?
解:作假设↔=22210:σσH 2
2211:σσ≠H
检验统计量 )
1,1(~
212
*2
*0
--=n n F S S
F H Y
X
拒绝域
()1,1(),,,;,,,{(1
2
212
1212121>--<=-
n F F n n F
F y y y x x x W n n αα
或
给定显著水平05.0=α,9,1321
==n n ,
则查表可得
20.4)8,12()1,1(025.0212
==--F n n F α,
28
.051
.31
)12,8(1)8,12()1,1(025.0975.02121====---F F n n F α
接受域为)20.4,
28.0(=W
又算得862.52*=X
S
,641.12*=Y
S
,从而
W
F ∈=572.3
故接受0
H ,即认为两种方法生产的产品中所含杂质的波动性无显著差异。
注②: 注意到附表4(F 分布的上侧
分位数表)中1),(21>n n F α,故在上述F 检
§4 单侧假设检验
(1)引例及说明
P102例
①原假设
H的选取原则: 检验产
品质量是否合格时,取
H为合格;检验
技术革新后某参数值有无显著变化时,取
H为变化不大。
②检验统计量的选取:与双侧检
验的相应情形一致。
③小概率事件的选取原则:给定α,依1H 选取。
④单侧检验拒绝域中的不等号方向与备择假设1H 中的一致。
(2)作法:(仅以下述几种情形为例)
①正态母体方差未知时,对均值的左边检验
作假设↔≥00:μμH 01:μμ<H
检验统计量 )1(~/0*0
--==n t n
S X T 时
μμμ
给定显著水平α,如图知有)
1(-n t α
使αα=--<)}1({n t T P ,故取拒绝域
})1(),,,{(21--<=n t T x x x W n α .
②大子样情形,对母体均值的右边检验
作假设↔
≤00:μμH :01μμ>H (其中
0μ已知)
检验统计量 )1,0(~
/00N n
S X U 时
近似
μμμ=-=
给定显著水平α,有αu 使αα≈≥}{u U P ,故取拒绝域
}),,,{(21αu U x x x W n ≥=
③对方差相等的两个正态母体均值之差的左边检验
作假设↔≥210:μμH 211:μμ<H 检验统计量
)
2(~
1111)()(212
1*
2
121*21212121-++
-=
+---===n n t n n S X X n n S X X T 时
时μμμμμμ
其中:2
)1()1(21*2
2*1
12
*22
-+-+-=n n S
n S n S
给定显著水平α,有)
2(21-+n n t
α
使
αα=-+-<)}2({21n n t T P ,故取拒绝域
}
)2(),,,;,,,{(21212121-+-<=n n t T y y y x x x W n n α。