当前位置：文档之家 › 正态总体均值及方差的假设检验表

正态总体均值及方差的假设检验表

  • 格式：doc
  • 大小：399.24 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

8.2-0单正态假设检验

8.2-0单正态假设检验
解 这里方差σ2未知，因此检验统计量为
u X 0 . S/ n
拒绝域为| u | u / 2 ．查表得 u / 2 = u0.025 = 1.96 ．
由于
| u | | x 0 | 0.4 50 1.22 1.96 , s/ n 4
所以接受H0，即认为总体的均值μ=0．
147，150，149，154，152，153，148，151, 155
假设零件长度服从正态分布，问这批零件是否
合格（取 = 0.05）？
解 这里是在总体方差 2 未知的情况下，检验假设 H0： 0 150 ，H1： 150 ．
在H0成立时，检验统计量
T X 0 ~ t(n 1) .
| t | | x 0 | 1.096 2.306 .
s/ n
所以接受H0，即认为这批零件合格．
三、正态总体方差的假设检验— 2 检验
设总体 X ~ N (, 2 ) 平 ．
, (X1，X2，…，Xn)为X 的样本，给定显著性水
1．当 已知时，方差 2的假设检验
H0： 2
(5)由数据计算得x 112.8, s 1.1358
故T 112.8 112.6 0.4659 2.4469 1.1358 7
故接受H 0 ,即可认为用热敏电阻测温仪间接测量温度无系统 误差。
例2 某车间加工一种零件，要求长度为150mm， 今从一批加工后的这种零件中抽取 9 个，测得长度如 下：

2
2 (n)
或 2

2 1
2 (n)
2


2 0
2


2 0
2


2

两个正态总体的假设检验

两个正态总体的假设检验

由样本观察值算出的 F 满足
F0.95 (9 , 9) 1 3.18 F 1.95 3.18 F0.05 (9 , 9) .
可见它不落入拒绝域，因此不能拒绝原假设 H0 ：σ12 = σ22 ，
从而认为两个总体的方差无显著差异。
注意：在 μ1 与 μ2 已知时，要检验假设 H0 ：σ12 = σ22 ，其
检验方法类同均值未知的情况，此时所采用的检验统计量是：
1 n1
2
(
X


)
i 1
n1 i 1
F
1 n2
2
(
Y


)
i 2
n2 i 1
其拒绝域参看表8-5。
( 2 )单边检验可作类似的讨论。
F0.05 (n1 , n2 ) .
8-5
概率学与数理统计
体的样本，且 μ1 与 μ2 未知。现在要检验假设 H0 ： σ2 = σ02 ；
H1： σ2 ≠ σ02 。在原假设 H0 成立的条件下，两个样本方差的
比应该在1附近随机地摆动，所以这个比不能太大又不能太小。
于是我们选取统计量
S12
F 2.
S2
( 8.21 )
显然，只有当 F 接近1时，才认为有 σ12 = σ22 。
10 10 2
18
由( 8.20 )式计算得
2.063 2.059
t0
3.3 .
0.0000072 (2 10)
对于 α =0.01，查自由度为18的 t 分布表得 t 0.005( 18 )=2.878。
由于| t0|=3. 3 > t 0.005( 18 )=2.878 ，于是拒绝原假设 H0 ：μ1 = μ2 。

正态总体方差的假设检验

正态总体方差的假设检验
方差计算公式为：$sigma^2 = frac{1}{N}sum_{i=1}^{N}(x_i mu)^2$，其中$N$是样本数量， $x_i$是每个样本值，$mu$是样本均 值。
方差的计算方法
简单方差
适用于数据量较小，且数据间相互独立的情况。
加权方差
适用于数据量较大，且数据间存在相关关系的 情况，需要考虑到每个数据点的重要程度。
配对样本方差检验
总结词
配对样本方差检验用于比较两个相关样本的方差是否相同。
详细描述
在配对样本方差检验中，我们首先需要设定一个零假设，即两个相关样本的方差无显著差异。然后， 通过计算检验统计量（如Wilcoxon秩和统计量或Stevens' Z统计量），我们可以评估零假设是否被拒 绝。如果零假设被拒绝，则可以得出两个相关样本方差不相同的结论。
方差齐性检验的目的是为了后续 的方差分析提供前提条件，确保 各组数据具有可比性。
方差分析
方差分析（ANOVA）是
1
用来比较多个正态总体均
值的差异是否显著的统计
方法。
4
方差分析的结果通常以p值 表示，若p值小于显著性水 平（如0.05），则认为各组 均值存在显著差异。
2
方差分析的前提条件是各
组数据具有方差齐性和正
正态总体方差假设检验的未来发展
改进假设检验方法
结合其他统计方法
结合其他统计方法，如贝叶斯推断、机器学习等， 可以更全面地分析数据和推断总体特征。
针对正态总体方差假设检验的局限性，未来 研究可以探索更灵活、适应性更强的检验方 法。
拓展应用领域
正态总体方差假设检验的应用领域可以进一 步拓展，特别是在大数据和复杂数据分析方 面。
数学表达式

两个正态总体的假设检验

两个正态总体的假设检验
两个正态总体的假设检验
有时，我们需要比较两总体的参数 有时，我们需要比较两总体的参数 是否存在显著差异。比如， 是否存在显著差异。比如，两个农作物 品种的产量，两种电子元件的使用寿命， 品种的产量，两种电子元件的使用寿命， 两种加工工艺对产品质量的影响， 两种加工工艺对产品质量的影响，两地 区的气候差异等等。 区的气候差异等等。
Fα2 (n1 − 1, n2 − 1) 和 F12 α (n1 − 1, n2 − 1) ，使 −
2
( P (F
P F < Fα (n1 − 1, n2 − 1) =
2 2
2
2
> F12 α −
2
）、（3） 由（2）、（ ）式可得检验的拒绝域为 ）、（
F < F1−(α 2) ( n1 − 1, n2 − 1) 及 F > Fα 2 ( n1 − 1, n2 − 1)
拒绝H 两种灯泡的平均寿命 所以拒绝 假设， 所以拒绝 0假设，即认为 A、B两种灯泡的平均寿命 、 两种灯泡的 有统计意义。 有统计意义。
两个正态总体的方差检验 问题： 问题： X ~ N µ , σ 2 , Y ~ N µ ,σ 2 1 1
(
)
未知
µ1 , µ2 ，检验假设 0：σ 12 = σ 22 检验假设H
所以拒绝原假设 H20，即认为两种玉米的产量差异 有统计意义。 有统计意义。
(
2
2
)
F检验 检验
S12 σ 12 F = 2 2 ~ F ( n1 − 1, n2 − 1) 由抽样分布知 S2 σ 2 2 S 若假设H 成立， 若假设 0成立，则 F = 12 ~ F ( n1 − 1, n2 − 1) S2
f (x )

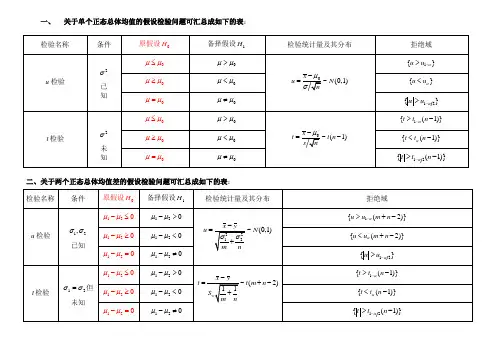
假设检验汇总表

假设检验汇总表

12
m

2 2
{u u (m n 2)}
n
{ u u1 2}
{t t1 (n 1)} {t t (n 1)}t 检验ຫໍສະໝຸດ 1 2 但未知
1 2 0 1 2 0
xy t ~ t (m n 2) 1 1 Sw m n
{u u1 }
已 知
0 0 0

n
~ N (0,1)
{u u }
{ u u1 2}
{t t1 (n 1)} {t t (n 1)}
t 检验
2
未 知
0 0
{ t t1 2 (n 1)}
二、关于两个正态总体均值差的假设检验问题可汇总成如下的表： 检验名称 条件 原假设 H 0 备择假设 H 1 检验统计量及其分布 拒绝域
2
(n 1)S 2
2 0
~ 2 (n 1)
2 2 (n 1)
2 21 ( n 1) 或 2 2 (n 1) 2 2
2 2 0
2 2 0
四、关于两个正态总体方差比的假设检验问题可汇总成如下的表： 条件 原假设 H 0
{ t t1 2 (n 1)}
三、关于单个正态总体方差的假设检验问题可汇总成如下的表： 条件 原假设 H 0
2 2 0
2 2 0
备择假设 H 1
2 2 0
2 2 0
检验统计量及其分布
拒绝域

已 知
2
( xi )
i 1 2 0
n
2 12 2
2 12 2
FF

双正态总体参数的假设检验

双正态总体参数的假设检验

§7.3 双正态总体参数的假设检验设样本1,,1n X X 取自正态总体211(,)N μσ，样本2,,1n Y Y 取自总体222(,)N μσ，两样本相互独立，它们的样本均值分别为∑==1111n i iX n X ，∑==2121n j jYn Y ，样本方差分别为∑=--=112121)(11n i i X X n S ，∑=--=212222)(11n j j Y Y n S 。

一、 关于两个正态总体方差比的假设检验以双侧检验：2221122210::σσσσ≠↔=H H 为例 选用检验统计量2221S S F =，它在原假设0H 成立的条件下服从F 分布)1,1(21--n n F ；记2221s s f O =表示检验统计量F 的样本观测值，则检验的P 值为⎪⎩⎪⎨⎧<=≥≥=≥=1),/1/1(21),(222212221O O O O f f F P f f F P P 如果如果σσσσ这种检验方法通常称为“F 检验”。

例7.3.1 甲乙两台车床分别加工某种轴，轴的直径分别服从正态分布),(211σμN ，),(2σμN ，从各自加工的轴中分别抽取若干根，测得其直径如下表所示：试问在显著性水平05.0=α下，两台车床加工的精度是否有显著差异？解：（1）依题意，考虑假设检验问题2221122210::σσσσ≠↔=H H （2）用F 检验，检验统计量为)6,7(~02221F S S F H =或)7,6(~/102122F S S F H =；（3）由样本观测值可得2164.021=s ，2729.022=s ，检验统计量的值为793.0/2221==s s f O 。

故检验的P 值为76.038.02)793.0/1/1(22221=⨯==≥=σσF P P 。

（4） 因为05.0>P ，所以不拒绝原假设0H ，即没有充分理由认为两种机床所加工轴的精度有显著差异。

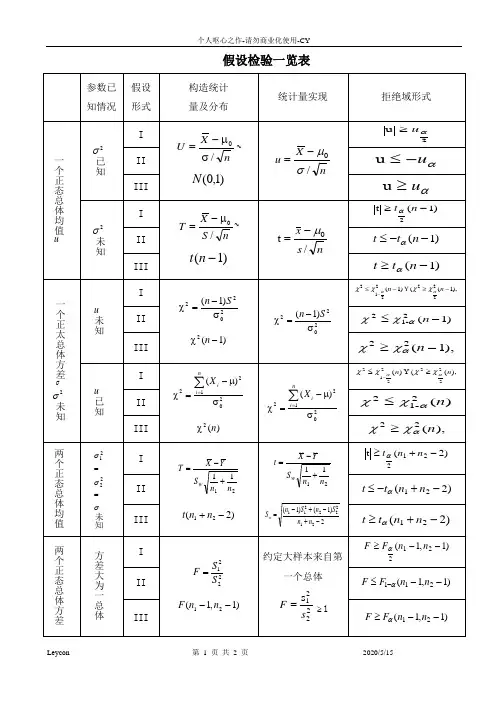
假设检验表-leycon

假设检验表-leycon

u u
t t (n 1)
2
未 知
2
T
II III I
~
t
x 0 s/ n
t t (n 1)
t (n 1)
(n 1)S 2 2 0
2
t t ( n 1)
2 2 2 (n 1) ( 2 (n 1), 1 2 2
一 个 正 太 总 体 方 差

u 未 知
II III I
2
2 (n 1)
n
(n 1)S 2 0
2
2 2 1- ( n 1)
2 2 (n 1),
未 知
2
u 已 知
II III

2
(X
i 1
i
)
2
2 2
1

2
2 (n) ( 2 (n), 2
2
方 差 大 为 一 总 体
S2 F 12 S2
F (n1 1, n2 1)
约定大样本来自第 一个总体
F F1 (n1 1, n2 1)
F
2 s1 2 1 s2
F F (n1 1, n2 1)
第 1 页 共 2 页
2012/12/27
个人呕心之作-请勿商业化使用-CY
u u
u u
2
U
X 0 S/ n
~ N (0,1)
u
x 0 s/ n
u u
代 替
u u
U X Y
2 2 S1 S 2 n1 n 2
u u
u x y
2 2 s1 s 2 n1 n2

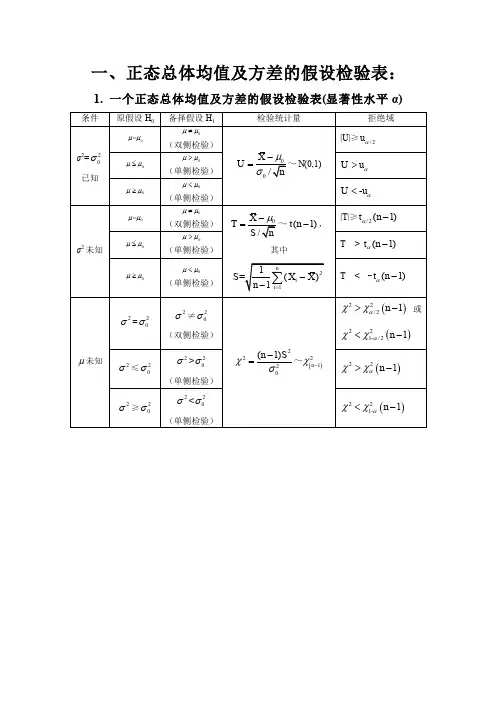
正态分布总体的区间估计与假设检验汇总表

正态分布总体的区间估计与假设检验汇总表

（单侧检验）
2
(n
1)S 2
2 0
～2n1
2
2 /2
n
1
或
2
2 1- / 2
n 1
2 2 n 1
2
≥
2 0
2
<
2 0
（单侧检验）
2
2 1-
n
1
2. 两个正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 备择假设 H1
检验统计量
拒绝域
12
，
2 2
已知
1 =2 1 2 1 2
1 2
1 2
（单侧检验）
SW
(n1 1)S12 (n2 1)S22 n1 n2 2
T < - t (n1 n2 2)
1，2
未知
2 1
=
2 2
2 1
≤
2 2
2 1
≠
2 2
（双侧检验）
2 1
>
2 2
（单侧检验）
F
S12 S22
～
F ( n1 - 1, n2 - 1)
F ≥ F /2 n1 1, n2 1
已知
0 / n
X
0 n
u
/2,
X
0 n
u
/2
2 未知 T X 0 ～ t(n 1) S/ n
X
S n 1
t / 2
n
1 ,
X
S n
1
t
/
2
n
1
方差 2
未知
2
(n 1)S 2
2 0
～2n1
(n 2 /
1)S 2

假设检验

假设检验

假设检验一、基本思想与基本步骤(一)假设检验问题[例1.6-1]某厂生产某种化纤的纤度X服从正态分布N(μ，0.042)，其中μ的设计值为1.40，每天都要对“μ=1.40”作例行检验，以观生产是否正常运行。

某天从生产线中随机抽取25根化纤，测得纤度值为:x1，x2，…，x25其纤度平均值=1.38，问当日生产是否正常。

几点评论:(1)这不是一个参数估计问题。

(2)这里要求对某个命题“μ=1.40”回答:是与否。

(3)这一类问题被称为(统计)假设检验问题。

(4)这类问题在质量管理中普遍存在。

(二)假设检验的基本步骤假设检验的基本思想是:根据所获样本，运用统计分析方法，对总体X的某种假设H0做出接受或拒绝的判断。

具体做法如下:1.建立假设H0:μ=1.40这是原假设，其意是:“与原设计一致”，“当日生产正常”等。

要使当日生产与1 40无差别是办不到的，若差异仅是由随机误差引起的，则可认为H0成立；若由其他特殊因素引起的，则认为差异显著，则应拒绝H0。

H1:μ≠1.40 这是备择假设，它是在原假设被拒绝时而应接受的假设。

在这里，备择假设还有两种设置形式，它们是:H12:μ<1.40，或H13:μ>1.40 备择假设的不同将会影响下面拒绝域的形式，今后称H0对H1的检验问题是双边假设检验问题H0对H12的检验问题是单边假设检验问题H0对H13的检验问题也是单边假设检验问题注:若假设是关于总体参数的某个命题，称为参数的假设检验问题，比如:H0:μ=μ0，H1:μ≠μ0，H0:σ2≤σ20，H1:σ2>σ20，H0:P≥P0，H1:P<P0，都是参数假设检验问题。

东莞德信诚精品培训课程(部分)(点击课程名称打开课程详细介绍)内审员系列培训课程查看详情TS16949五大工具与QC/QA/QE品质管理类查看详情 JIT东莞德信诚公开课培训计划>>> 培训报名表下载>>> /download/dgSignUp.doc2.选择检验统计量，给出拒绝的形式这个假设检验问题涉及正态均值μ。

正态总体的均值和方差的假设检验

正态总体的均值和方差的假设检验

12
n1

2 2
n2
~ N (0,1)
给定α 0.05,
(当H 0成立时)
由 Φ(u0.025 ) 0.975, 查表可得 uα / 2 u0.025 1.96
(3)拒绝域: W1={(x1, x2, ∙∙∙, xn, y1, y2, ∙∙∙, yn)||u| u /2=1.96},
3. μ为未知，关于σ 2的检验（χ 2检验法）
设X 1 , X 2 , , X n是来自正态总体 N ( μ, σ 2 )的一样本，
其中μ, σ 2未知，检验水平为 α，检验σ 2步骤为：
1 假设H0 : 2 0 2 , H1: 2 0 2 ;
X1 , X 2 ,, X n为来自总体X的样本，
2 2 2 2 X ~ N ( μ1 , σ1 ),Y ~ N ( μ2 , σ 2 ), σ1 60, σ 2 80,问
两台机床生产的产品重量有无显著差异( =0.05)？ 解 本题归结为检验假设
(1) H0 : 1 2 , H1: 1 2 ,
(2)取检验的统计量为 U ( X Y ) /
解 (1)
本题归结为检验假设
H 0 : μ 800,
H1 : μ 800;
40，n 9 X 800 (2)选择统计量 U 9 40
当H0成立时,U~N(0,1).
(3)给定显著性水平 = 0.05,由正态分布函数表 查得u /2=u0.025 =1.96,从而得检验的拒绝域为 W1={(x1 , x2 , ∙∙∙ , xn) :|u| u 0.025 =1.96 }； (4) 由样本值计算U的观测值为
x 0 s / n

7-2正态总体参数的检验

7-2正态总体参数的检验
第二节 正态总体参数的假设检验
一、单个正态总体均值的检验 二、两个正态总体均值差的检验 三、正态总体方差的检验
同上节) 标准要求长度是32.5毫米 毫米. 例2(同上节 某工厂生产的一种螺钉 标准要求长度是 同上节 某工厂生产的一种螺钉,标准要求长度是 毫米
实际生产的产品，其长度 假定服从正态分布N( σ 未知， 实际生产的产品，其长度X 假定服从正态分布 µ,σ2 ) ,σ2 未知， 现从该厂生产的一批产品中抽取6件 得尺寸数据如下: 现从该厂生产的一批产品中抽取 件, 得尺寸数据如下
(1)与(4); (2)与(5)的拒绝域形式相同 与 的拒绝域形式相同. 与 的拒绝域形式相同
一、单个正态总体均值的检验
是来自N( σ 的样本 的样本, 设x1,…,xn是来自 µ,σ2)的样本 关于µ的三种检验问题是 (µ0是个已知数 是个已知数)
(1) H0 : µ ≤ µ0 vs H1 : µ > µ0 (2) H0 : µ ≥ µ0 vs H1 : µ < µ0 (3) H0 : µ = µ0 vs H1 : µ ≠ µ0
对于检验问题 对于检验问题
(2) H0 : µ ≥ µ0 vs H1 : µ < µ0
x − µ0
仍选用u统计量 u = 选用 统计量 相应的拒绝域的形式为: 相应的拒绝域的形式为
取显著性水平为α 取显著性水平为α，使c满足 P 0 (u ≤ c) = α 满足 µ
由于μ = μ 0时，u ~ N(0,1),故 c = uα,如图 故 , 因此拒绝域为: 因此拒绝域为 或等价地: 或等价地 φ(x)
检 H0 : µ = µ0 vs H1 : µ ≠ µ0 验
x − µ0 s/ n
接受域为: 接受域为

两正态分布均值差检验

两正态分布均值差检验

两正态总体均值差的假设检验基于Wolfram Mathematica ,给出了两正态分布Ν[μ1,σ1]、Ν[μ2,σ2]总体均值差μ1-μ2在两总体方差已知、未知但相等、未知但样本量相等、未知但已知方差比、未知近似、未知精确的假设检验方法。

"一.两总体方差σ12=σ102、σ22=σ202已知,Z 检验"定理1:U =X 1--X 2--(μ1-μ2)σ12Ｎ[0,1],σ12=需要Needs ["HypothesisTesting`"]σ1=1;σ2=2;X1=伪随机变数RandomVariate [正态分布NormalDistribution [3,σ1],1000];X2=伪随机变数RandomVariate [正态分布NormalDistribution [2,σ2],1500];μ0=1.02;α=0.01;n1=长度Length [X1];n2=长度Length [X2];m =平均值Mean [X1]-平均值Mean [X2];σ=u =m -μ0σ;"1.双侧Z 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [正态分布NormalDistribution [0,1],绝对值Abs [u ]]ZTest {X1,X2}, σ12,σ22 ,μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal" "2.右侧Z 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [正态分布NormalDistribution [0,1],u ]Z 检验ZTest {X1,X2}, σ12,σ22 ,μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater" "3.左侧Z 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [正态分布NormalDistribution [0,1],u ]Z 检验ZTest {X1,X2}, σ12,σ22 ,μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"1.双侧Z 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0.6402322.右侧Z 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0.3201163.左侧Z 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ00.679884"二.两总体方差σ12=σ22未知,T 检验"定理2:T =X 1--X 2--(μ1-μ2)S Wt n 1+n 2-2 ，S W =2 正态分布\\正态分布统计分析\\两正态分布均值差检验.nb需要Needs ["HypothesisTesting`"]σ1=σ2=2;X1=伪随机变数RandomVariate [正态分布NormalDistribution [3,σ1],1000];X2=伪随机变数RandomVariate [正态分布NormalDistribution [2,σ2],1500];μ0=1.05;α=0.01;n1=长度Length [X1];n2=长度Length [X2];m =平均值Mean [X1]-平均值Mean [X2];V1=方差Variance [X1];V2=方差Variance [X2];Sw =t =m -μ0Sw;"1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [学生t 分布StudentTDistribution [n1+n2-2],绝对值Abs [t ]]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal"]"2.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [学生t 分布StudentTDistribution [n1+n2-2],t ]T 检验TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater"]"3.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [学生t 分布StudentTDistribution [n1+n2-2],t ]T 检验TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"]1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ00.1818342.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ00.9090833.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ00.0909169正态分布\\正态分布统计分析\\两正态分布均值差检验.nb3"三.两总体方差σ12、σ22未知,但样本容量n1=n2=n,T检验"定理3:T=X-(μ1-μ2)S X n t n-1 ,X=X1-X2.4正态分布\\正态分布统计分析\\两正态分布均值差检验.nb需要Needs ["HypothesisTesting`"]n =1000;X1=伪随机变数RandomVariate [正态分布NormalDistribution [3,2],n ];X2=伪随机变数RandomVariate [正态分布NormalDistribution [2,1],n ];μ0=1.0;α=0.01;X =X1-X2;m =平均值Mean [X ];S =标准偏差StandardDeviation [X ];t =m -μ0Sn;"1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [学生t 分布StudentTDistribution [n -1],绝对值Abs [t ]]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal"]"2.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [学生t 分布StudentTDistribution [n -1],t ]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater"]"3.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [学生t 分布StudentTDistribution [n -1],t ]T 检验TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"]1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ00.3169872.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ00.8415063.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ00.158494"四.两总体方差σ12、σ22未知,但已知方差比σ12σ22=r,T 检验"正态分布\\正态分布统计分析\\两正态分布均值差检验.nb5定理4:X 1--X 2--(μ1-μ2)S X 1t n 1-1 ,X 1--X 2--(μ1-μ2)S X2t n 2-1 ,X 1--X 2--(μ1-μ2)t n 1+n 2-2 .需要Needs ["HypothesisTesting`"]X1=伪随机变数RandomVariate [正态分布NormalDistribution [3,2],1200];X2=伪随机变数RandomVariate [正态分布NormalDistribution [2,1],2500];μ0=1.1;α=0.01;r =4;n1=长度Length [X1];n2=长度Length [X2];m =平均值Mean [X1]-平均值Mean [X2];S1=标准偏差StandardDeviation [X1];S2=标准偏差StandardDeviation [X2];"(一) X 1--X 2--(μ1-μ2)S X1t (n 1-1)"Sw =S1t =m -μ0Sw;"1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [学生t 分布StudentTDistribution [n1-1],绝对值Abs [t ]]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal"]"2.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [学生t 分布StudentTDistribution [n1-1],t ]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater"]"3.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [学生t 分布StudentTDistribution [n1-1],t ]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"]"(二) X 1--X 2--(μ1-μ2)SX 2t (n 2-1)"Sw =S2t =m -μ0Sw;6 正态分布\\正态分布统计分析\\两正态分布均值差检验.nb"1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [学生t 分布StudentTDistribution [n2-1],绝对值Abs [t ]]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal"]"2.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [学生t 分布StudentTDistribution [n2-1],t ]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater"]"3.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [学生t 分布StudentTDistribution [n2-1],t ]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"]"(三X 1--X 2--(μ1-μ2)t (n 1+n 2-2)"Sw = 1n1+(n2-1)S12++(n2-1)S22;t =m -μ0Sw;"1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [学生t 分布StudentTDistribution [n2-1],绝对值Abs [t ]]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal"]"2.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [学生t 分布StudentTDistribution [n2-1],t ]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater"]"3.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [学生t 分布StudentTDistribution [n2-1],t]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"](一)X 1--X 2--(μ1-μ2)S X 1t (n 1-1)1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ00.05165612.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ00.974172正态分布\\正态分布统计分析\\两正态分布均值差检验.nb73.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ00.0258281(二)X 1--X 2--(μ1-μ2)S X 2t (n 2-1)1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ00.04846952.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ00.9757653.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0.0242347(三X 1--X 2--(μ1-μ2)t (n 1+n 2-2)1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ00.09177842.右侧T 检验H 0:μ1-μ2≤μ0,H1:μ1-μ2>μ00.9541113.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ00.0458892"五.两总体方差σ12、σ22未知,近似T检验"定理5:X --Y --(μ1-μ2)~t (n ),n =舍入Round++.8 正态分布\\正态分布统计分析\\两正态分布均值差检验.nb需要Needs ["HypothesisTesting`"]X1=伪随机变数RandomVariate [正态分布NormalDistribution [3,2],1800];X2=伪随机变数RandomVariate [正态分布NormalDistribution [2,1],1000];μ0=1.0;α=0.01;m =平均值Mean [X1]-平均值Mean [X2];V1=方差Variance [X1];V2=方差Variance [X2];n =舍入Round+2+;t =m -μ0"1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [学生t 分布StudentTDistribution [n ],绝对值Abs [t ]]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal"]"2.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [学生t 分布StudentTDistribution [n ],t ]T 检验TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater"]"3.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [学生t 分布StudentTDistribution [n ],t ]T 检验TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"]1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ00.6178232.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ00.6910893.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ00.308911"六.两总体方差σ12、σ22未知,T 检验(n 1<n 2)"正态分布\\正态分布统计分析\\两正态分布均值差检验.nb9定理6:T =X 1--X 2--(μ1-μ2)S X nt n 1-1 ,X 3i =X 2i i =1,2,⋯,n 1 ,X i =X 1iX 3i+X 3-X 2,X =1n 1i =1n 1X i ,S X =需要Needs ["HypothesisTesting`"]X1=伪随机变数RandomVariate [正态分布NormalDistribution [3,2],1200];X2=伪随机变数RandomVariate [正态分布NormalDistribution [2,1],1500];μ0=1.0;α=0.01;n1=长度Length [X1];n2=长度Length [X2];m1=平均值Mean [X1];m2=平均值Mean [X2];X3=X2[[1;;n1]];m3=平均值Mean [X3];X =X1-平方根Sqrt n1 n2 X3+平方根Sqrt n1 n2 m3-m2;m =平均值Mean [X ];S =标准偏差StandardDeviation [X ];t =m -μ0Sn1;"1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ0"p =2 1-⋯CDF [学生t 分布StudentTDistribution [n1-1],绝对值Abs [t ]]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"不等Unequal"]"2.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ0"p =1-⋯CDF [学生t 分布StudentTDistribution [n1-1],t ]TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"大于Greater"]"3.左侧T 检验H 0:μ1-μ2≥μ0,H 1:μ1-μ2<μ0"p =⋯CDF [学生t 分布StudentTDistribution [n1-1],t ]T 检验TTest [{X1,X2},μ0,"TestDataTable",备择假设AlternativeHypothesis →"小于Less"]1.双侧T 检验H 0:μ1-μ2=μ0,H 1:μ-μ2≠μ00.6180772.右侧T 检验H 0:μ1-μ2≤μ0,H 1:μ1-μ2>μ00.30903810 正态分布\\正态分布统计分析\\两正态分布均值差检验.nb正态分布\\正态分布统计分析\\两正态分布均值差检验.nb113.左侧T检验H0:μ1-μ2≥μ0,H1:μ1-μ2<μ00.690962。

8.2正态总体均值的假设检验

8.2正态总体均值的假设检验

t t ( n1 n2 2).
x y 因为 t 4.295, 1 1 sw 10 10
t0.05 (18) 1.7341,
所以拒绝 H 0 ,
即认为建议的新操作方法较原来的方法为优.
例5 有甲、乙两台机床加工相同的产品, 从这两台机床加工 的产品中随机地抽取若干件, 测得产品直径(单位:mm)为 机床甲: 20.5, 19.8, 19.7, 20.4, 20.1, 20.0, 19.0, 19.9
X 0 P Z / n
拒绝域为 Z Z
或 H0： 0；H1：0
X 0 P Z / n
拒绝域为 Z Z
2、方差未知 问题：总体 X~N（，2），2未知 假设 H0：=0；H1：≠0 构造T统计量 T X 0 ~ t (n 1)
t检验 双边检验
X 0 由 P t 2 (n 1) S n 确定拒绝域 T t 2 (n 1) x 0 如果统计量的观测值 T t 2 (n 1) S n
则拒绝原假设；否则接受原假设
S
n
例2 化工厂用自动包装机包装化肥，每包重量服从正态 分布，额定重量为100公斤。某日开工后，为了确定包 装机这天的工作是否正常，随机抽取9袋化肥，称得平 均重量为99.978，均方差为1.212，能否认为这天的包 装机工作正常？（=0.1） 解 由题意可知：化肥重量X~N（，2），0=100 方差未知，要求对均值进行检验，采用T检验法。
得 k t / 2 (n1 n2 2).
故拒绝域为
( x y) t t / 2 ( n1 n2 2). 1 1 sw n1 n2

正态总体均值与方差的假设检验

正态总体均值与方差的假设检验

, 其中 Sw2
(n1
1)
S* 1n1
2
(n2
1)
S* 2 n2
2
.
n1 n2 2
当H0为真时,根据第二章§2.3定理2.9知, 定理2.9
t ~ t(n1 n2 2).
其拒绝域旳形式为
|x y|
W {x: sw
1
1
t (n1 n2 2)},
2
n1 n2
第一类错误旳概率为：
P{H0 为真拒绝
问全部住户消费数据旳总体方差为0.3是否可信?
解 按题意要检验 H0 : 2 0.3, H1 : 2 0.3, n 9, x 5.91, sn*2 6.05 / 9,
查表得
2 0.975
(8)
2.18,
2 0.025
(8)
17.5,
于是
(n 1)sn*2
02
6.05 20.17 17.5, 0.3
此处 k 的值由下式确定 :
P12＝
2 2
S* 2 1n1
S* 2 2 n2
k1
P12＝
2 2
S* 2 1n1
S* 2 2 n2
k2
要使 P{H0 为真拒绝 H0} , 为了计算
简单，令
P
S* 2 1n1
2 1
S* 2 2n
22
22 ,
H1:
2 1
22
,
当 H0 为真时,
E
(
S* 1n1
2
)
12
2 2
E
(
S* 1n2
2
),
当 H1 为真时,
E( S12 )
2 1
2 2

34两个正态总体均值和方差的假设检验

34两个正态总体均值和方差的假设检验

(n1 n2 2)
(
x sw
y 1 n1


1 n2
k)
2
概率统计
在显著性水平 下, H0 的拒绝域:
x y
sw
11 n1 n2
t (n1 n2 2)
2
注:
当

2 1


2 2
2
未知时
检验假设 H0 : 1 2 , H1 : 1 2
H1
:

2 1


2 2
单边检验
H1
:

2 1


2 2
同上面双边检验的讨论类似，可得 H0的拒绝域为:
s12 s22

F (n1
1, n2
1)
习惯上亦称两个总体 方差相等的检验为： 两总体方差齐性的检验
或
s12 s22

F1 (n1
1, n2
1)
概率统计
例2. 现要检测两批葡萄酒的醇含量，分别对它们
设有 n 对相互独立的观察结果：
( X1 ,Y1 ) , ( X 2 ,Y2 ) , , ( X n ,Yn )
令：D1 X1 Y1 , D2 X 2 Y2 , , Dn ( X n ,Yn ) 则 D1 , D2 , , Dn相互独立。又由于 D1 , D2 , , Dn 是由同一因素所引起的，所以可认为它们服从同 一分布。
例4 现要比较甲、乙两种橡胶制成的轮胎的耐磨性。
今从甲、乙两种轮胎中各随机的取 8 个，又从 两组中各取一个组成一对，共 8 对； 再随机的取 8 架飞机，将 8 对轮胎随机地搭配 给这 8 架飞机作耐磨性试验，当飞机飞行了一 定时间后测得轮胎的磨损量的数据(单位：毫克) 如下：

两个正态总体均值差和方差的假设检验

两个正态总体均值差和方差的假设检验

方差齐性检验是检验 两个正态总体方差是 否相等的统计方法。
常用的方差齐性检验 方法有：Levene检验、 Bartlett检验和Welch 检验。
Levene检验基于方差 分析，通过比较不同 组间的方差来判断方 差是否齐性。
Bartlett检验基于 Kruskal-Wallis秩和 检验，通过比较不同 组间的中位数和四分 位距来判断方差是否 齐性。
独立样本的均值检验
1
独立样本的均值检验是用来比较两个独立正态总 体的均值是否存在显著差异的统计方法。
2
常用的独立样本均值检验方法包括t检验和z检验， 其中t检验适用于小样本和大样本，而z检验适用 于大样本。
3
在进行独立样本均值检验时，需要满足独立性、 正态性和方差齐性的假设，以确保检验结果的准 确性和可靠性。
根据研究目的和数据类型，选择合适的统计量 来描述样本数据。
确定临界值
根据统计量的分布和显著性水平，确定临界值。
计算样本统计量
根据样本数据计算所选统计量的值。
做出决策
将样本统计量的值与临界值进行比较，做出接受 或拒绝原假设的决策。
解读结果
根据决策结果解读研究问题，给出结论和建议。
Part
02
两个正态总体均值的假设检验
Part
05
结论与展望
假设检验的优缺点
理论基础坚实
假设检验基于概率论和统计学原理，具有坚实的理论基础。
操作简便
假设检验提供了清晰的步骤和标准，方便研究者进行操作。
假设检验的优缺点
• 实用性强：假设检验广泛应用于各个领域，为科学研究和实践提供了有效的工具。
假设检验的优缺点
01
对数据要求较高
假设检验对数据的分布、样本量 等有一定的要求，不符合条件的 样本可能导致检验结果不准确。

一个正态总体期望与方差的假设检验

一个正态总体期望与方差的假设检验
第八章
第二节 一个正态总体 期望与方差的假设检验
一、期望值的假设检验
检验 二、方差的假设检验－
2
一、期望值的假设检验
2 2 1、方差 0 为已知时对期望值 的检验— u 检验
设样本 X 1 , X 2 ,
, X n 来自正态总体 N ( , 2 ), 方
差 2已知,对 的检验问题由上节中的五个步骤来进行. ①建立假设 关于正态均值 常用的三对假设 (a) H0 : 0 ,H1 : 0 ; (双边假设检验问题) (b) H0 : 0 ,H1 : 0 ; (单边假设检验问题) } (c) H0 : 0 ,H1 : 0 . 选择哪一种假设应根据问题的需要.
② 检验统计量都选择 U 统计量
U
X 0
/ n
~ N (0,1)
(8.2.1)
③ 确定显著性水平
显著性水平 的大小应根据研究问题的需要而定,
一般为0.05. ④ 确定临界值,给出拒绝域 对于三种不同的假设,其拒绝域如图所示,其中u1 / 2 是标准正态分布的 1 分位数, 其他意义相同. 2
即样本观测值落在拒绝域之外, 故接受原假设, 认为该批金 属丝折断力的方差与64无显著差异.
以上对方差的检验属于双侧检验,另外还有单侧检验:
2 2 H0 : 2 0 ;H1 : 2 0
(8.2.8)
2 2 H0 : 2 0 ;H1 : 2 0 (8.2.9) 关于假设检验问题 2 2 (8.2.10) H0 : 2 0 ;H1 : 2 0 它与假设检验问题式(8.2.8)在同一显著性水平α下的检验 方法是一样的,其他的单侧检验也类同. 例4 某车间生产一种保险丝,规定保险丝熔化时间的 方差不得超过400.今从一批产品中抽处25个,测得其熔化时 间的方差为388.58, 试根据所给数据, 检验这批产品的方差 是否符合要求(α=0.05). 已知保险丝的熔化时间服从正态 分布.

方差已知时总体均值的双侧假设检

方差已知时总体均值的双侧假设检

一、方差已知时总体均值的双侧假设检100202221:,:,,),(),...,,(μμμμσσσμ≠==*H H N X X X n 要检验假设为已知常数的样本是取自正态总体设}|{|,,:,00000K X C X H X >-==*μμμμμμ所以临界域应有形式太远波动而不偏离附近随机地应在则样本均值为真如果原假设的无偏估计为由于样本均值 )1,0(~/00N n X U σμ-=由于}|{|}|{|,,2/2/2/αααααu U C u U P u ≥==≥这样就得到了临界域使可查出相应的临界值下于是在给定显著性水平n x u x x x n /),...,,(0021σμ-=算出再根据样本观察值找临界值u α/2示意图..,;.:,||,0002/αμμα率恰好等于此时犯第一类错误的概异原假设无差认为此时的总体均值与否则接受原假设有明显差异认为总体的均值此时与则拒绝原假设即若H H u u C u =≥∈*例:设某厂一车间生产的钮扣,其直径据经验服从正态分布N(μ,5.22).为了检验这一车间生产是否正常,现抽取容量n=100的样本,得样本均值为26.56,要求在显著性水平α=0.05下检验假设H0:μ0=26.解：26:,26:10≠=μμH H 备择假设提出原假设)1,0(~100/2.526N X U -=建立统计量05.0}96.1|100/2.526{|96.1,05.0025.02/=≥-===X P u u 即查得对于给定的显著性水平αα.,96.108.1100/2.52656.26100/2.526||0认为生产是正常的从而接受原假设而H x u <=-=-= 例 由经验知某零件的重量X~N 2=15，=0.05；技术革新后，抽出6个零件，测得重量为（单位：克）14.7 15.1 14.8 15.0 15.2 14.6，已知方差不变，试统计推断，平均重量是否仍为15克？=0.05）解 由题意可知：零件重量X~N 2），且技术2=0.052，要求对均值进行检验，采用U 检验法。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

或
2 ≤ 02
2 ≥ 02
2 > 02
2 < 02
2 个正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 a1=a2
2 12 ， 2
备择假设 H1 a1≠a2 a1>a2 a1<a2 a1≠a2 a1>a2
检验统计量
拒绝域 |U|≥ u( n - 1) a
a=a0 已 知 方差 2
c2 =
1 n 2 x - a0 ) ～c (2n) 2 å ( i s i =1
轾n n 2 2 犏 x i - a0 ) x i - a0 ) 邋 ( ( 犏 i =1 , i =1 犏 骣 骣 a a 犏 c2 琪 c (2n) 琪 1琪 犏 ( n) 琪 2 桫 桫 2 臌
( )
U≥ u( n - 1) 2a
( ) ( )
U≤- u( n - 1) 2a |T|≥ t( n - 1) a
( )
σ 未知
2
a≤a0 a≥a0
T=
x - a0 ～ t( n- 1) S n- 1
T≥ t( n - 1) 2a
( )
( )
T≤- t( n - 1) 2a
2 = 02
a= a0 已 知
(
已知
( )
( )
2 12 = 2
a1≤a2 a1≥a2
T=
未知
Z ～ t( n- 1) S n- 1
T≥ t( n - 1) 2a
( )
( )
T≤- t( n - 1) 2a
单正态总体均值及方差的区间估计(置信度 1-α)
待估参数 条件 检验统计量 拒绝域
2 s 2 =s 0
U=
已知 均值 a
或
骣 a F ≤ F( n1 - 1,n2 - 1) 琪 1琪 桫 2
F ≥ F( n1 - 1, n2 - 1) ( a )
F ≤ F( n1 - 1, n2 - 1) ( a )
F ( n1 - 1, n2 - 1)
2 个配对样本正态总体均值的假设检验表(显著性水平 α)
2 Z=ξ-η～N(a1-a2， 12 + 2 )，Zi=ξi-ηi.
条件
原假设 H0 a1=a2
备择假设 H1 a1≠a2 a1>a2 a1<a2 a1≠a2 a1>a2 a1<a2
检验统计量
拒绝域 |U|≥ u( n - 1) a
2 12 ， 2
a1≤a2 a1≥a2 a1=a2
U=
Z
2 s +s 2 n 2 1
( ) )
～ N(0,1)
U≥ u( n - 1) 1 - a U≤- u( n - 1) 2a |T|≥ t( n - 1) a
轾 1 犏 x - h ? t( n1 +n2 - 2) ( a ) SW 犏 n1 臌
(
)
1 n2
t( n1 +n2 - 2)

2
n2 i a1 n1 i a2
i 1 i 1 n2
n1
2
a1， a2 已 知
12 ～ 2 2 2
轾 骣 a 骣 a 犏 F( n1 ,n2 ) 琪 1A, F( n1 ,n2 ) 琪 A 琪 琪 犏 2 桫 2 桫 臌
2 ≠ 02
1 n 2 c = 2 å ( x i - a0 ) ～c (2n) s 0 i =1
2
骣பைடு நூலகம்a c 2 > c (2n) 琪 琪 或 2 桫 骣 a c 2 < c (2n) 琪 1琪 桫 2
c 2 > c (2n) ( a ) c 2 < c (2n) ( 1 - a )
2 ≤ 02 2 ≥ 02
a1≤a2 a1≥a2 a1=a2 a1≤a2
U=
x -h
2 s 12 s 2 + n1 n2
( ) )
～ N(0,1)
U≥ u( n - 1) 1 - a U≤- u( n - 1) 2a
(
已知
( )
( )
T=
=
2 1
2 2
x -h ～ 1 1 SW + n1 n2
|T|≥ t( n1 +n2 - 2) a
2 1
2 2
(x - h ) - ( a - a ) ～
1
已知 均值 a1-a2
2 12 = 2
s s + n1 n2
2 1
2 2
轾 s 12 犏 x h ? u a 犏 n1 犏 臌
(
)
2 s2 n2
N(0,1)
(x - h ) - ( a - a ) ～
1 2
SW
未知
1 1 + n1 n2
2 > 02 2 < 02
2 = 02
a 未知
2 ≠ 02
nS 2 c = 2 ～c (2n- 1) s0
2
骣 a c 2 > c (2n- 1) 琪 琪 2 桫 骣 a c 2 < c (2n - 1) 琪 1琪 桫 2
c 2 > c (2n - 1) ( a )
c 2 < c (2n - 1) ( 1 - a )
a 未知
c2 =
nS 2 ～c (2n- 1) 2 s0
轾 犏 nS 2 犏 nS 2 , 犏 骣 骣 a a 2 犏 c (2n - 1) 琪 1琪 c ( n - 1) 琪 琪 犏 2 桫 桫 2 臌
2 个正态总体均值差及方差比的区间估计(置信度 1-α)
待估参数 条件 检验统计量 拒绝域
2
，
T≥ t( n1 +n2 - 2) 2a
( ) ( )
未知 a1≥a2 a1<a2
t( n1 +n2 - 2) ,
n S 2 + n2 S 22 SW = 1 1 n1 + n2 - 2
T≤- t( n1 +n2 - 2) 2a
2 12 = 2
2 12 ≠ 2
a1， a2 已 知
2 12 ≤ 2 2 12 ≥ 2 2 12 > 2 2 12 < 2
F ≤ F( n1 ,n2 ) ( a )
2 12 = 2
2 12 ≠ 2
a1， a2 未 知
2 12 ≤ 2 2 12 ≥ 2 2 12 > 2 2 12 < 2
nS n -1 F = ( 1 2) ～ n2 S2 ( n2 - 1)
2 1 1
骣 a F ≥ F( n1 - 1,n2 - 1) 琪 琪 2 桫
F( n1 - 1,n2 - 1)
n S + n2 S SW = ，A= n1 + n2 - 2
2 1 1
2 2
n1å ( x i - a2 ) n2 å ( x i - a2 )
i =1 i =1 n1
n2
2
2
，B=(
( n2 - 1) n1S12
2 n1 - 1) n2 S2
．
1 2 x i - a1 ) å ( n i =1 F= 1 n ～ 1 2 å ( hi - a2 ) n2 i =1
n
骣 a F ≥ F( n1 ,n2 ) 琪 琪 2 桫 骣 a F ≤ F( n1 ,n2 ) 琪 1琪 桫 2
F ≥ F( n1 ,n2 ) ( a )
或
F ( n1, n2 )
x -a ～ N(0,1) s0 n1
轾 s0 s 犏 x u( n- 1) ( a ) ,x + 0 u( n- 1) ( a ) 犏 n n 臌
未知
2
T=
x -a ～ t( n- 1) S n- 1
轾 犏 x 犏 臌
S S t( n- 1) ( a ) ,x + t n- 1 ( a ) n- 1 n- 1 ( )
2 方差 12 2
a1， a2 未 知
F( n1 ,n2 )
( n - 1) n S ( n - 1) n S
2 1
2 1 1 2 2 2
s 12 ～ 2 s2
轾 骣 a 骣 a 犏 F( n1 - 1,n2 - 1) 琪 1B, F( n1 - 1,n2 - 1) 琪 1B 琪 琪 犏 桫 2 桫 2 臌
正态总体均值及方差的假设检验表：
单正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 a=a0
2 σ2= 0
备择假设 H1 a≠a0 a>a0 a<a0 a≠a0 a>a0 a<a0
检验统计量
拒绝域 |U|≥ u( n - 1) a
a≤a0 a≥a0 a=a0
U=
已知
x - a0 ～ N(0,1) s0 n1