第五章 控制系统的稳定性分析(含习题解答)

第5章“控制系统的李雅普诺夫稳定性分析”练习题及答案.doc第5章 “控制系统的李雅普诺夫稳定性分析”练习题及答案5.1 判断下列函数的正定性1) 2221231213()2322V x x x x x x x =++-+x 2) 222123121323()82822V x x x x x x x x x =++-+-x 3) 22131223()2V x x x x x x =+-+x解1) T T 211()130101V A -??==-x x x x x , 因为顺序主⼦式2120,50,13->=>- 2111302011--=> 所以0>A ，()V x 为正定函数。

2) T T 841()421111V -??==---x x Ax x x , 因为主⼦式8481218,2,10,0,70,10,421111-->==>=>--421164421680111---=++---<- 所以A 不定，()V x 为不定函数。

3) T T 1212110()1001V -??==-x x Ax x x , 因为顺序主⼦式1110,10,1->=-<- 121211011001041--=--<所以A 为不定矩阵，()V x 为不定函数。

5.2 ⽤李雅普诺夫第⼀⽅法判定下列系统在平衡状态的稳定性。

2211211222212212()()x x x x x x x x x x x x =-+++=--++解解⽅程组 22121122212212()0()0x x x x x x x x x x ?-+++=?--++=?只有⼀个实孤⽴平衡点（0，0）。

在（0，0）处将系统近似线性化，得** 1111x x -??=?--，由于原系统为定常系统，且的特征根1s i =-±均具有负实部，于是根定理5.3可知系统在原点（0，0）附近⼀致渐近稳定。

控制工程基础习题解答第五章5-1．已知开环系统的传递函数如下，试用罗斯-赫尔维茨判据判别其闭环稳定性。

（1）. ()()()()()32110+++=s s s s s H s G （2）. ()()()()()()38.05.022.0++++=s s s s s s H s G （3）. ()()()5060030010022++=s s s s H s G （4）.()()()2481322+++=s s s s s H s G 解：（1）. 特征方程为01016523=+++s s s100141051610123s s s s第一列全部大于零，所以闭环稳定。

（2）. 特征方程为04.04.13.43.4234=++++s s s s4.097.04.097.34.13.44.03.4101234s s s s s 第一列全部大于零，所以闭环稳定。

（3）. 特征方程为010050600300234=+++s s s100012001005006001005030001234-s s s s s第一列有小于零的数存在，所以闭环不稳定，符号变化了两次，有两个右极点。

（4）. 特征方程为013248234=++++s s s s124100380012410038 18924138=5033801241038= 503124100380012410038= 所有主子行列式全大于零，所以闭环稳定。

5-2．已知单位负反馈系统的开环传递函数如下()⎪⎪⎭⎫ ⎝⎛++=1222n n s s s Ks G ωζω式中s rad n /90=ω，2.0=ζ。

试确定K 取何值闭环稳定。

解：方法1：特征方程为0810081003623=+++K s s s 36008100810036810036081001810036222≤≥≥-⨯=K K K K KK36810081003681001810036≤≥-⨯=K K K得当360<<K 时，闭环稳定，当36时，闭环临界稳定。

第五章 状态反馈和状态观测器3-5-1 已知系统结构图如图题3-5-1图所示。

(1)写出系统状态空间表达式；(2)试设计一个状态反馈矩阵，将闭环极点特征值配置在j 53±-上。

)(t y题3-5-1图【解】：方法一：根据系统结构直接设状态变量如题3-5-1图所示，写状态空间表达式：[]x y u x x 10112101=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--= 23111=⎥⎦⎤⎢⎣⎡--=c c U rank U系统能控，可以设计状态反馈阵。

设状态反馈阵为][21k k K = 状态反馈控制规律为：Kx r u -= 求希望特征多项式：34625)3()(*22++=++=s s s s f求加入反馈后的系统特征多项式：)22()3()(1212k s k k s bK A sI s f ++-++=+-=依据极点配置的定义求反馈矩阵：]1316[131634)22(6)3(21112=⎩⎨⎧==⇒⎩⎨⎧=+=+-K k k k k k 方法二：[][][]1316)346(311110)(*10211=++⎥⎦⎤⎢⎣⎡--==--I A A A f U K c方法三：（若不考虑原受控对象的结构，仅从配置极点位置的角度出发）求系统传递函数写出能控标准型：2321)111()()(2++-=+-+=s s ss s s U s Y []xy u x x 10103210-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 求系统希望特征多项式：34625)3()(*22++=++=s s s s f求状态反馈矩阵K ~：[][][]33236234~21=--==k k K [][][][]5.05.031111010111=⎥⎦⎤⎢⎣⎡--==--Ab bP⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=105.05.011A P P P []1316~==P K K依据系统传递函数写出能控标准型ss s s s s s U s Y 2310)2)(1(10)()(23++=++= []x y u x x 0010100320100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=求系统希望特征多项式：464]1)1)[(2()(*232+++=+++=s s s s s s f求状态反馈矩阵：[][][]144342604321=---==k k k K 。

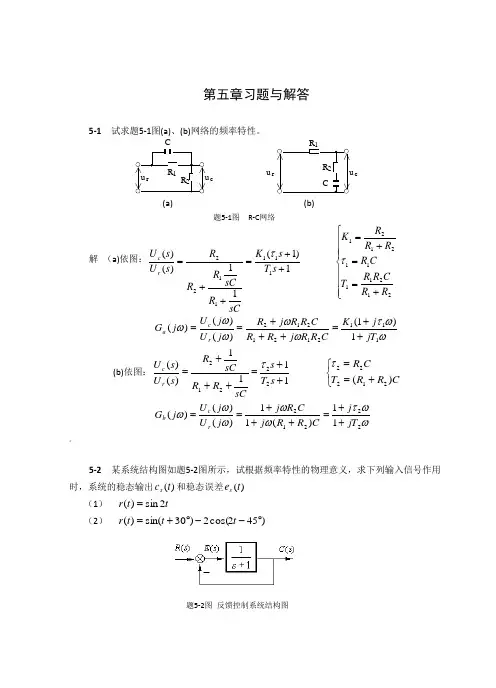
第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。

u r R1u cR2CR2R1u r u c(a) (b)题5-1图R-C网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图：⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++=="5-2某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs和稳态误差)(tes（1）tt r2sin)(=（2）)452cos(2)30sin()(︒--︒+=ttt r题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=-系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ （2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ>)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应 h t e e t tt()..=-+≥--11808049试求系统频率特性。

题型：选择题题目：关于系统稳定的说法错误的是【】A．线性系统稳定性与输入无关B．线性系统稳定性与系统初始状态无关C．非线性系统稳定性与系统初始状态无关D．非线性系统稳定性与系统初始状态有关分析与提示：线性系统稳定性与输入无关；非线性系统稳定性与系统初始状态有关。

答案：C习题二题型：填空题题目：判别系统稳定性的出发点是系统特征方程的根必须为或为具有负实部的复数，即系统的特征根必须全部在是系统稳定的充要条件。

分析与提示：判别系统稳定性的出发点是系统特征方程的根必须为负实数或为具有负实部的复数，即系统的特征根必须全部在复平面的左半平面是系统稳定的充要条件。

答案：负实数、复平面的左半平面习题三题型：选择题题目：一个线性系统稳定与否取决于【】A．系统的结构和参数B．系统的输入C．系统的干扰D．系统的初始状态分析与提示：线性系统稳定与否取决于系统本身的结构和参数。

答案：A习题四题型：填空题题目：若系统在的影响下，响应随着时间的推移，逐渐衰减并回到平衡位置，则称该系统是稳定的分析与提示：若系统在初始状态的影响下（零输入），响应随着时间的推移，逐渐衰减并趋向于零(回到平衡位置)，则称该系统是稳定的；反之，若系统的零输入响应发散，则系统是不稳定的。

答案：初始状态习题五题型：填空题题目：系统的稳定决定于的解。

分析与提示：系统的稳定决定于特征方程的解。

答案：特征方程题型：填空题题目：胡尔维兹（Hurwitz ）判据、劳斯（Routh ）判据又称为 判据。

分析与提示：胡尔维兹（Hurwitz ）判据、劳斯（Routh ）判据，又称为代数稳定性判据。

答案：代数稳定性习题二题型：填空题题目：利用胡尔维兹判据，则系统稳定的充要条件为：特征方程的各项系数均为 ；各阶子行列式都 。

分析与提示：胡尔维兹判据系统稳定的充要条件为：特征方程的各项系数均为正；各阶子行列式都大于零。

答案：正、大于零习题三题型：计算题题目：系统的特征方程为010532234=++++s s s s用胡尔维兹判据判别系统的稳定性。

自动控制理论第五章习题汇总填空题1、系统的频率响应与正弦输入信号之间的关系称为频率响应2、在正弦输入信号的作用下，系统输入的稳态分量称为频率响应简答题：5-2、什么是最小相位系统及非最小相位系统？最小相位系统的主要特点是什么？答在s平面上，开环零、极点均为负实部的系统称为最小相位系统；反之，开环零点或极点中具有正实部的系统称为非最小相位系统。

最小相位系统的主要特点是：相位滞后最小，并且幅频特性与相频特性有惟一的确定关系。

如果知道最小相位系统的幅频特性，可惟一地确定系统的开环传递函数。

5-3、什么是系统的频率响应？什么是幅频特性？什么是相频特性？什么是频率特性？答对于稳定的线性系统，当输入信号为正弦信号时，系统的稳态输出仍为同频率的正弦信号，只是幅值和相位发生了改变，如图5-3所示，称这种过程为系统的频率响应。

图5-3称为系统的幅频特性，它是频率的函数；称为系统的相频特性，它是频率的函数：称为系统的频率特性。

稳定系统的频率特性可通过实验的方法确定。

计算题5-1、设某控制系统的开环传递函数为)()(s H s G =)10016()12.0(752+++s s s s 试绘制该系统的Bode 图，并确定剪切频率c ω的值。

解：Bode 图如下所示剪切频率为s rad c /75.0=ω。

5-2、某系统的结构图和Nyquist 图如图(a)和(b)所示，图中2)1(1)(+=s s s G 23)1()(+=s s s H 试判断闭环系统稳定性，并决定闭环特征方程正实部根的个数。

解：由系统方框图求得内环传递函数为：ss s s s s s H s G s G +++++=+23452474)1()()(1)( 内环的特征方程：04742345=++++s s s s s由Routh 稳定判据：1:0310:16:44:171:01234s s s s s由此可知，本系统开环传函在S 平面的右半部无开环极点，即P=0。

第5章 “控制系统的李雅普诺夫稳定性分析”练习题及答案5.1 判断下列函数的正定性1) 2221231213()2322V x x x x x x x =++-+x 2) 222123121323()82822V x x x x x x x x x =++-+-x 3) 22131223()2V x x x x x x =+-+x解1) T T 211()130101V A -⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦x x x x x , 因为顺序主子式2120,50,13->=>- 2111302011--=> 所以0>A ，()V x 为正定函数。

2) T T 841()421111V -⎡⎤⎢⎥==--⎢⎥⎢⎥-⎣⎦x x Ax x x , 因为主子式8481218,2,10,0,70,10,421111-->==>=>--841421164421680111---=++---<- 所以A 不定，()V x 为不定函数。

3) T T 1212110()1001V -⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦x x Ax x x , 因为顺序主子式1110,10,1->=-<- 121211011001041--=--<所以A 为不定矩阵，()V x 为不定函数。

5.2 用李雅普诺夫第一方法判定下列系统在平衡状态的稳定性。

2211211222212212()()x x x x x x x x x x x x =-+++=--++解解方程组 22121122212212()0()0x x x x x x x x x x ⎧-+++=⎨--++=⎩只有一个实孤立平衡点（0，0）。

在（0，0）处将系统近似线性化，得**1111x x -⎡⎤=⎢⎥--⎣⎦，由于原系统为定常系统，且矩阵1111-⎡⎤⎢⎥--⎣⎦的特征根1s i =-±均具有负实部，于是根定理5.3可知系统在原点（0，0）附近一致渐近稳定。

自动控制原理课后习题答案(总26页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除第一章引论1-1 试描述自动控制系统基本组成，并比较开环控制系统和闭环控制系统的特点。

答：自动控制系统一般都是反馈控制系统，主要由控制装置、被控部分、测量元件组成。

控制装置是由具有一定职能的各种基本元件组成的，按其职能分，主要有给定元件、比较元件、校正元件和放大元件。

如下图所示为自动控制系统的基本组成。

开环控制系统是指控制器与被控对象之间只有顺向作用，而没有反向联系的控制过程。

此时，系统构成没有传感器对输出信号的检测部分。

开环控制的特点是：输出不影响输入，结构简单，通常容易实现；系统的精度与组成的元器件精度密切相关；系统的稳定性不是主要问题；系统的控制精度取决于系统事先的调整精度，对于工作过程中受到的扰动或特性参数的变化无法自动补偿。

闭环控制的特点是：输出影响输入，即通过传感器检测输出信号，然后将此信号与输入信号比较，再将其偏差送入控制器，所以能削弱或抑制干扰；可由低精度元件组成高精度系统。

闭环系统与开环系统比较的关键，是在于其结构有无反馈环节。

1-2 请说明自动控制系统的基本性能要求。

答：自动控制系统的基本要求概括来讲，就是要求系统具有稳定性、快速性和准确性。

稳定性是对系统的基本要求，不稳定的系统不能实现预定任务。

稳定性通常由系统的结构决定与外界因素无关。

对恒值系统，要求当系统受到扰动后，经过一定时间的调整能够回到原来的期望值（例如恒温控制系统）。

对随动系统，被控制量始终跟踪参量的变化（例如炮轰飞机装置）。

快速性是对过渡过程的形式和快慢提出要求，因此快速性一般也称为动态特性。

在系统稳定的前提下，希望过渡过程进行得越快越好，但如果要求过渡过程时间很短，可能使动态误差过大，合理的设计应该兼顾这两方面的要求。

准确性用稳态误差来衡量。

在给定输入信号作用下，当系统达到稳态后，其实际输出与所期望的输出之差叫做给定稳态误差。

机械控制工程基础第五章练习习题及解答习题一题型：选择题题目：关于系统稳定的说法错误的是【】A．线性系统稳定性与输入无关B．线性系统稳定性与系统初始状态无关C．非线性系统稳定性与系统初始状态无关D．非线性系统稳定性与系统初始状态有关分析与提示：线性系统稳定性与输入无关；非线性系统稳定性与系统初始状态有关。

答案：C习题二题型：填空题题目：判别系统稳定性的出发点是系统特征方程的根必须为或为具有负实部的复数，即系统的特征根必须全部在是系统稳定的充要条件。

分析与提示：判别系统稳定性的出发点是系统特征方程的根必须为负实数或为具有负实部的复数，即系统的特征根必须全部在复平面的左半平面是系统稳定的充要条件。

答案：负实数、复平面的左半平面习题三题型：选择题题目：一个线性系统稳定与否取决于【】A．系统的结构和参数B．系统的输入C．系统的干扰D．系统的初始状态分析与提示：线性系统稳定与否取决于系统本身的结构和参数。

答案：A习题四题型：填空题题目：若系统在的影响下，响应随着时间的推移，逐渐衰减并回到平衡位置，则称该系统是稳定的分析与提示：若系统在初始状态的影响下（零输入），响应随着时间的推移，逐渐衰减并趋向于零(回到平衡位置)，则称该系统是稳定的；反之，若系统的零输入响应发散，则系统是不稳定的。

答案：初始状态习题五题型：填空题题目：系统的稳定决定于的解。

分析与提示：系统的稳定决定于特征方程的解。

答案：特征方程习题一题型：填空题题目：胡尔维兹（Hurwitz）判据、劳斯（Routh）判据又称为判据。

分析与提示：胡尔维兹（Hurwitz）判据、劳斯（Routh）判据，又称为代数稳定性判据。

答案：代数稳定性习题二题型：填空题题目：利用胡尔维兹判据，则系统稳定的充要条件为：特征方程的各项系数均为；各阶子行列式都。

分析与提示：胡尔维兹判据系统稳定的充要条件为：特征方程的各项系数均为正；各阶子行列式都大于零。

答案：正、大于零习题三题型：计算题题目：系统的特征方程为2s4?s3?3s2?5s?10?0用胡尔维兹判据判别系统的稳定性。

前言本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。

本书对该教材中的习题给予了详细解答，可帮助同学学习和理解教材的内容。

由于习题数量较多，难易程度不同，虽然主要对象是研究型大学自动化专业本科学生，但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。

书中第5、6、8章习题由高立群教授组织编选和解答；第4、7 章由井元伟教授组织编选和解答，第1、2章由郑艳副教授组织编选和解答。

由于时间比较仓促，可能存在错误，请读者批评、指正。

另外有些题目解法和答案并不唯一，这里一般只给出一种解法和答案。

编者 2005年5月第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示，设输入为1u ，输出为2u ，试自选状态变量并列写出其状态空间表达式。

图P2.1解 此题可采样机理分析法，首先根据电路定律列写微分方程，再选择状态变量，求得相应的系统状态空间表达式。

也可以先由电路图求得系统传递函数，再由传递函数求得系统状态空间表达式。

这里采样机理分析法。

设1C 两端电压为1c u ，2C 两端的电压为2c u ，则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =，22c x u =，由式(1)和(2)得：1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为：12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。

《现代控制理论》第5章习题解答5.1 已知系统的状态空间模型为Cx y Bu Ax x =+=, ，画出加入状态反馈后的系统结构图，写出其状态空间表达式。

答：具有状态反馈的闭环系统状态空间模型为：u Kx =−+v ()xA BK x Bv y Cx=−+=相应的闭环系统结构图为闭环系统结构图5.2画出状态反馈和输出反馈的结构图，并写出状态反馈和输出反馈的闭环系统状态空间模型。

答：具有状态反馈的闭环系统状态空间模型为u Kx =−+v ()xA BK x Bv y Cx=−+=相应的反馈控制系统结构图为具有输出反馈的闭环系统状态空间模型为u Fy =−+v ()x A BFC x Bv y Cx=−+=相应的反馈控制系统结构图为后案网 ww w.kh d5.3 状态反馈对系统的能控性和能观性有什么影响？输出反馈对系统能控性和能观性的影响如何？答：状态反馈不改变系统的能控性，但不一定能保持系统的能观性。

输出反馈不改变系统的能控性和能观性。

5.4 通过检验能控性矩阵是否满秩的方法证明定理5.1.1。

答：加入状态反馈后得到闭环系统K S ，其状态空间模型为()x A BK x Bv y Cx=−+=开环系统的能控性矩阵为0S 1[,][]n c A B BAB A B −Γ="闭环系统K S 的能控性矩阵为 1[(),][()()]n cK A BK B B A BK B A BK B −Γ−=−−"由于222()()()()(A BK B AB BKBA BKB A ABK BKA BKBK B)A B AB KB B KAB KBKB −=−−=−−+=−−−#以此类推，总可以写成的线性组合。

因此，存在一个适当非奇异的矩阵U ，使得()m A BK B −1,,,m m A B A B AB B −[(),][,]cK c A BK B A B U Γ−=Γ由此可得：若rank([,])c A B n Γ=，即有个线性无关的列向量，则n [(),]cK A BK B Γ−也有个线性无关的列向量，故n rank([(),])cK A BK B n Γ−=5.5 状态反馈和输出反馈各有什么优缺点。

第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。