Ti2+离子能级结构的理论计算
- 格式:docx
- 大小:57.71 KB
- 文档页数:7

离子的极化率和极化力公式,并标明所有参数的物理意义
离子的极化率
在电场作用下离子的电子云分布偏离原子核,造成负电荷中心偏离,产生了诱导偶极矩。
诱导偶极矩pI正比于有效电场强度E,pI=αE。
比例系数α称离子极化率,其单位是C·m2/V。
离子半径越大,核外电子越多,极化率越大。
负离子极化率一般大于正离子。
负离子价越高,极化率越大;正离子价越高,极化率越小。
含d电子多的正离子极化率大。
离子极化率多由经验或半经验公式计算得到。
也有一些理论计算,如下:
离子的极化力公式
一个离子能够使其他离子极化的能力称为极化力。
一个离子的极化力就决定于这个离子所产生电场的大小,电场愈大,则极化力也愈强。
离子极化能力大小的三个主要因素,即离子半径、离子电荷和离子的电子层构型。
用离子势来表示离子极化力,Z是离子价电荷数,R 是离子半径。
离子势反映了离子电荷密度的大小,决定了离子的电场强度,如果阳离子的电荷越高,半径越小, 则该离子极化力越强,这种标度对解释8电子构型的离子极化力是很成功。
用离子有效核电荷与半径来标度极化力,离子极化力=Z*2/r,离子有效核电荷Z*=Z-S,Z为离子的核电荷数,S为离子中所有电子对外面假设的加合电子的屏蔽系数之和,它与离子的电子构型有关。
计算对非惰气构型离子也适用,与化合物性质符合得较好。
以上两种标度把离子看成是带电荷的圆球来考虑,下面是另一种在量子力学中的标度。

离子极化和离子晶体的晶格能——离子极化能的理论计算和适用于所有离子晶体的晶格能公式
离子极化和离子晶体的晶格能是由离子极化的作用和晶体的晶格结构共同决定的。
离子极
化是由电子的位移而引起的,当一个负离子周围有一个或更多的正离子时,它们之间发生
离子极化,这时负离子就有了一个近似虚拟电荷,而当它离开正离子时,这个虚拟电荷消失。
晶格能是一个晶体晶格中多个原子的相互作用定义的,它取决于原子的表面形状,原
子的重量大小,原子的极化能和原子力的感应。
为了理论计算晶格能,一般用户采用了离子极化(IP)和共价能(CP)有效势函数法。
在
这种情况下,由离子极化能而产生的晶格能是依靠了有效势函数法来理论计算的。
有效势
函数法中定义了两个参数,即离子极化系数k和共价能参数C,这两个参数用于描述离子
极化能和共价能之间的相互关系。
在实际计算中,可以选择不同的参数值来定义离子的极
化能,从而计算出晶格能。
克拉平克斯(Krampen)和柏金斯(Broms)提出了一种适用于所有离子晶体的晶格能公式。
根据这个公式,晶格能的计算可以用以下公式表示:U=S1+S2+S3,其中S1表示由离子极
化能而产生的能量,S2表示从共价能而产生的能量,而S3表示由极化能和共价能之间的
交互相互作用而产生的能量。
这个公式已成为计算晶格能的标准。
由此可见,离子极化和离子晶体的晶格能是由离子极化和晶格结构共同决定的,理论计算
晶格能大都采用有效势函数法,而晶格能的计算则可以通过克拉平克斯和柏金斯的晶格能
公式来完成。

二维光子晶体能带结构计算
计算二维光子晶体的能带结构可以采用所谓的平面波展开法(Plane wave expansion method)或所谓的有限元法(Finite element method)。
其中,平面波展开法将晶体的电场和磁场分别表示为周期性平面波的展开,并通过求解Maxwell方程来获得能带结构和色
散曲线。
有限元法则将计算区域分割为有限的小块,对每个小块进行数值求解,最终通过求解矩阵本征值问题来获得能带结构。
需要注意的是,二维光子晶体的能带结构通常可以通过简化的
K点采样方案来计算,而不是像传统的固体晶格那样通过整个倒空间的完整采样来计算。
具体实施计算过程可能因采用的具体方法而有所不同,因此建议在实际计算中查阅相关文献或软件文档以获得更详细的指导。

二维光子晶体能带结构计算二维光子晶体是由周期性幻灯片形状的材料构成的结构,其中存在禁带,可以控制光的传播和吸收特性。
能带结构计算是研究光子晶体特性的重要方法之一、本文将介绍二维光子晶体能带结构的计算方法及其在光学器件设计中的应用。
能带结构是指在固体中,电子或光子在能量-波矢空间中的能量分布情况。
对于二维光子晶体而言,能带结构可以通过求解带有布拉格波动方程的频率-波矢关系得到。
计算二维光子晶体能带结构的方法主要有两种,分别是耦合平面波方法和有限差分时间域方法。
耦合平面波方法是计算光子晶体能带结构的传统方法之一、该方法通过展开光的电磁场为平面波形式,然后将其代入光的麦克斯韦方程进行求解。
耦合平面波方法可以得到光子晶体的色散曲线,从而得到能带结构。
该方法的优点是计算速度快、精度较高,但对计算资源要求较高。
有限差分时间域方法是一种近年来较为流行的计算二维光子晶体能带结构的方法。
该方法基于有限差分的原理,将光的电磁场离散化为有限差分点。
然后通过求解麦克斯韦方程的差分形式,得到光的传播模式和色散曲线。
有限差分时间域方法可以更加直观地展示二维光子晶体的能带结构及其演化规律。
该方法的优点是计算精度高、适合于复杂结构的计算,但计算耗时较长。
二维光子晶体的能带结构对于光学器件的设计具有重要意义。
例如,通过调控光子晶体的结构参数,可以实现光子晶体中禁带的控制,从而实现特定波长光的波导效应。
此外,光子晶体中的能带结构还可以用于设计可调谐的光学滤波器和调制器等器件。
总结起来,二维光子晶体能带结构的计算是研究光子晶体特性的重要方法之一、耦合平面波方法和有限差分时间域方法是计算二维光子晶体能带结构的两种常见方法。
通过计算二维光子晶体的能带结构,可以实现光的波导效应和设计可调谐的光学器件。
随着计算技术的发展,二维光子晶体能带结构的计算方法将会进一步完善和广泛应用。



第28卷第3期2012年6月 分 子 科 学 学 报 JOURNAL OF MOLECULAR SCIENCE Vol.28No.3 June 2012收稿日期:2012-02-23基金项目:辽宁省自然科学基金计划项目(201102198);辽宁省教育厅项目(L2010518);沈阳师范大学实验室主任基金重点项目.联系人简介:刘跃(1965-),女,教授,主要从事聚合机理、材料设计、计算化学等研究.E-mail:yueliusd@163.com[文章编号]1000-9035(2012)03-0248-04磷掺杂锐钛矿二氧化钛能带结构的从头计算研究王丽丽,李 阳,刘 颖,刘 跃*(沈阳师范大学化学与生命科学学院,辽宁沈阳110034)[摘 要] 用密度泛函方法优化了锐钛矿二氧化钛及其磷掺杂锐钛矿二氧化钛的晶体结构.研究揭示了用超胞模型研究未掺杂和P掺杂锐钛矿TiO2能带结构和态密度的可行性.计算结果对于提高TiO2光催化活性有意义.[关键词] 锐钛矿;光催化性;掺杂;密度泛函[中图分类号] O 649 [学科代码] 150·30 [文献标识码] A 0 引 言TiO2具有优异的光催化、敏化等特性,受到人们广泛关注[1].TiO2有四方金红石、锐钛矿和正交板钛矿3种晶型结构.每个Ti 4+离子在O2-离子围成的八面体空隙中,O原子周围相邻3个Ti原子.金红石型TiO2的空间群为P42/mnm(136),晶体常数a=b=0.459 4nm,c=0.295 9nm.其中每个八面体与2个八面体共用一棱边,另与8个八面体共用一顶点(见图1a).锐钛矿型TiO2的空间群为I41/amd(141),晶体常数a=b=0.377 6nm,c=0.948 6nm.每个八面体与4个八面体共用一棱边,另与4个八面体共用一顶点(见图1b).板钛矿型TiO2的空间群为Pbca(61),晶体常数a=0.916 6nm,b=0.543 6nm,c=0.513 5nm(见图1c).(a):金红石(1×1×2);(b):锐钛矿(3×1×1);(c)板钛矿单晶胞图1 TiO2晶型结构示意图纳米尺度的薄膜和颗粒中锐钛矿结构占优势.在催化和光电化学的应用方面,锐钛矿相比金红石相更有效[2].但是锐钛矿型TiO2带隙较宽(Eg=3.2eV),只能吸收波长较短的紫外光.从机理角度[3-6]用计算化学方法[7-9]研究材料理论问题[10-11]行之有效.因此本文用量子化学从头计算方法,研究掺杂对锐钛矿型TiO2能带结构的影响.研究结果对于提高TiO2光催化效率有意义[12-13].1 计算方法Materials Studio 5.5软件CASTEP(Cambridge serial total energy package)模块[14-15];密度泛函理论,广义梯度近似(GGA,general gradient approximation)下的RPBE(revised Perdew Burke Ernzer-hof)泛函方案;超软赝势(ultrasoft pseudopotential);平面波截断能400eV,自洽迭代过程总能量收敛限2×10-6 eV/原子,布里渊区k点网格选取3×5×2.几何全优化,分别计算了磷取代氧的掺杂和未掺杂的TiO2的能带结构和态密度.2 结果与讨论各种类型TiO2素晶胞中原子的分数坐标示于表1,其他原子坐标可以根据对称性得到.锐钛矿TiO2素晶胞中含4个等价的Ti和8个等价的O.用1个P原子取代任何1个等价O原子,计算结果相同.表1 TiO2晶胞中原子的分数坐标原子金红石锐钛矿板钛矿Ti(0.0000,0.0000,0.0000)(0.0000,0.0000,0.0000)(0.127 0,0.386 8,0.373 0)(0.010 0,0.155 0,0.180 0)O(0.304 8,0.304 8,0.000)(0.0000,0.500 0,0.042 0)(0.230 0,0.395 0,0.035 0) 曹红红等用1个Sn4+取代锐钛矿TiO2素晶胞中4个Ti 4+中的1个[13],掺杂比为0.25.高掺杂比不利于光催化.实际上半导体的掺杂比一般都很小.为了与实验一致,我们将锐钛矿TiO2的2个素晶胞合并为一个超胞,用1个P取代16个等价O中的一个,掺杂比为0.062 5.锐钛矿超晶胞参数优化结果见表2.表2 锐钛矿TiO2超晶胞参数优化值nm参数a b c未掺杂TiO20.763 4 0.381 8 0.982 6P掺杂TiO20.742 4 0.383 3 1.180 4 图2为计算得到的掺杂和未掺杂TiO2的能带结构,由图2a可以看出,采用超胞模型,理论计算得到的纯锐钛矿TiO2禁带宽度(带隙)是2.18eV,小于实验结果3.2eV.GGA计算得到的结果通常要小于实验值.曹红红和侯清玉等人计算锐钛矿TiO2素晶胞禁带宽度结果分别是2.12和2.26eV[2,12].尽管超胞模型从表面上破坏了原来素晶胞的对称性,计算结果说明素晶胞的内禀对称性仍然保留不变,因此采用超胞模型研究掺杂锐钛矿TiO2的能带结构和态密度问题是可行的.采用超胞模型的缺点是没有对称性的帮助,计算负担加大.(a)TiO2;(b)P图2 掺杂TiO2能带结构942第3期 王丽丽,等:磷掺杂锐钛矿二氧化钛能带结构的从头计算研究采用超胞模型得到P掺杂后的TiO2带隙值如图2b,在价带和导带之间形成3条P的2p轨道的杂质能级.除了杂质能带外,原来的带隙也稍有减小.电子可以从价带跃迁到中间杂质能级,再从中间杂质能级跃迁到导带,所以杂质能级有助于扩大吸收波长范围,实现可见光范围内的光催化.图3a为TiO2的总态密度和组分态密度.可以看出,TiO2价带和导带都包含Ti的3d轨道和O的2p轨道成分,价带主要由O的2p轨道组成,导带主要由Ti的3d轨道组成.所以TiO2中既含有离子键又含有共价键.图3b为P掺杂TiO2的总态密度和组分态密度,从图3b可以看出,P掺杂后的TiO2的态密度整体向能量负方向移动,空带能级降低有利于空带接受电子,表明P掺杂TiO2的氧化能力更强,TiO2光催化活性增强.杂质能级由O的2p轨道和Ti的3d轨道杂化形成.由于形成了杂质能级,当掺杂率较高时,杂质能级会成为电子-空穴复合中心,不利于光催化.(a):TiO2总态密度,O和P组分态密度;(b):P掺杂TiO2总态密度,P和Ti组分态密度图3 总态密度和组分态密度3 结 论TiO2是目前发展潜力最大的多功能新型环保光催化剂之一,已被广泛应用于越来越多的领域,因此如何更加有效提高TiO2光催化效率仍是有待深入研究的课题,需要理论计算与实验相结合,用计算机模拟的方式对材料的新性能进行预测,再用实验方法加以验证.本工作采用超胞模型,对磷掺杂的锐钛矿二氧化钛的能带结构和态密度进行了研究,并且与锐钛矿二氧化钛的能带结构和态密度进行了比较.结果表明,P掺杂锐钛矿二氧化钛产生杂质能级,扩大了可见光吸收范围,提高二氧化钛光催化效率.[参 考 文 献][1] 汝强,胡社军,邱秀丽.[J].华南师范大学学报:自然科学版,2009(4):52-56.[2] 曹红红,黄海波.[J].北京航空航天大学学报,2005,31(2):251-254.[3] LIU Y,DREW M G B,LIU Y.[J].J Magn Magn Mater,2011,323:945-953.[4] LIU Y,DREW M G B,LIU Y,et al.[J].J Magn Magn Mater,2010,322(21):3342-3345.[5] LIU Y,DREW M G B,WANG J,et al.[J].J Magn Magn Mater,2010,322(3):366-374.[6] LIU Y,DREW M G B,LIU Y.[J].J Magn Magn Mater,2010,322:814-818.[7] LIU Y,LIU Y,DREW M G B.[J].Struct Chem,2010,21(1):21-28.[8] LIU Y,DREW M G B,LIU Y.[J].J Mol Struct:THEOCHEM,2007,809:29-37.[9] LIU Y,WANG Q,LIU Y,et al.[J].Chem Phys Lett,2003,373(3/4):338-343.[10] LIU Y,LIU B,LIU Y.[J].J Chem Educ,2011,88(3):295-298.[11] LIU Y,LIU B,LIU Y,et al.[J].J Math Chem,2011,49:2089-2108.052 分子科学学报 第28卷 [12] 侯清玉,张跃,张涛.[J].光学学报,2008,28(7):1347-1352.[13] 曹红红,陈强,王天民.[J].稀有金属材料与工程,2008,37(2):219-222.[14] SEGALL M D,LINDAN P J D,PROBERT M J,et al.[J].J Phys Condens Matter,2002,14:2717-2743.[15] 张福兰,李来才.[J].分子科学学报,2011,27(1):49-53.Ab initio study on the band structure of P-doped anatase TiO2WANG Li-li,LI Yang,LIU Ying,LIU Yue*(Colledge of Chemistry and Life Science,Shengyang Normal Universty,Shenyang 110034,China)Abstract:The microstructures of pure and P-doped anatase TiO2were optimized by ab initio method.Evidences for the possibility of studying band structures and density states using the density functionaltheory(DFT)with super cell model of P-doped anatase TiO2were investigated.The results obtainedby the calculations on the P-doped anatase TiO2are significant for analyzing the mechanism of photo-catalysis of TiO2and for improving catalytic activity of anatase TiO2.Keywords:anatase titania;photo-catalysis;dope;density functional theory152第3期 王丽丽,等:磷掺杂锐钛矿二氧化钛能带结构的从头计算研究。
`TiO复合2对TiO的复合一般可分为半导体复合,表面光敏化和贵金属沉积三种类型。
2复合作用能实现对TiO中光生电子-空穴的分离,同时复合物也增加对可见光的2吸收。
(1)半导体复合将TiO与其它能带结构不同的半导体进行复合,称为半导体复合。
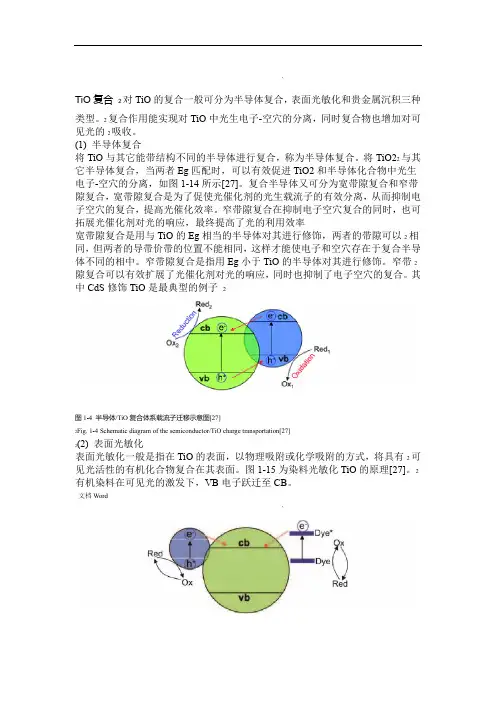
将TiO22与其它半导体复合,当两者Eg匹配时,可以有效促进TiO2和半导体化合物中光生电子-空穴的分离,如图1-14所示[27]。
复合半导体又可分为宽带隙复合和窄带隙复合,宽带隙复合是为了促使光催化剂的光生载流子的有效分离,从而抑制电子空穴的复合,提高光催化效率。
窄带隙复合在抑制电子空穴复合的同时,也可拓展光催化剂对光的响应,最终提高了光的利用效率宽带隙复合是用与TiO的Eg相当的半导体对其进行修饰,两者的带隙可以2相同,但两者的导带价带的位置不能相同,这样才能使电子和空穴存在于复合半导体不同的相中。
窄带隙复合是指用Eg小于TiO的半导体对其进行修饰。
窄带2隙复合可以有效扩展了光催化剂对光的响应,同时也抑制了电子空穴的复合。
其中CdS修饰TiO是最典型的例子2图1-4 半导体/TiO复合体系载流子迁移示意图[27]2Fig. 1-4 Schematic diagram of the semiconductor/TiO charge transportation[27]2(2)表面光敏化表面光敏化一般是指在TiO的表面,以物理吸附或化学吸附的方式,将具有2可见光活性的有机化合物复合在其表面。
图1-15为染料光敏化TiO的原理[27]。
2有机染料在可见光的激发下,VB电子跃迁至CB。
文档Word`图1-5 TiO表面光敏化示意图[27]2Fig. 1-5 Schematic diagram of the TiO photosensitization[27]2(3)表面贵金属沉积贵金属沉积一般是指在TiO的表面沉积某种贵金属形成纳米级的量子点,以2改变体系中的电子分布结构,从而增强TiO的光催化活性。

五-类氢离子能级和光谱的计算摘要:利用玻尔理论和索默菲尔德的轨道原理,考虑到相对论效应和自旋轨道相互作用,与几种线性类氢离子相关的精确能级和光谱的理论分析和数值计算,并进行列表、讨论以及总结。
最后,总结了类氢离子的能级和光谱以及精细结构的影响因素和规律。
关键字:类氢离子;精细结构;能级;光谱;氢离子0引言光谱学是研究原子结构的重要因素,可以获得有关物质组成的信息。
通过sommerfeld 轨道校正和Lamb —Retherford 的结果,并考虑自旋角动量和电子的轨道角动量,得到了氢和类氢离子精细结构值的理论计算公式。
能级的水平定义是,原子由围绕原子核和原子核运行的电子组成,因为电子具有不同的能量。
因此,它们围绕核根据不同轨道运行,也就是,不同能量的电子处于不同的水平。
根据氢离子的能量水平,光谱和能级在类氢离子的氦离子的精细结构进行了分析计算,以便更好地了解和理解氢的系统的能级和光谱。
王建伟[10]等人用玻尔理论和力分析法计算了氢离子能量和光谱的精细结构,强调了影响氢离子水平的三个因素,氢类离子满足产生光谱过程中的转变规律。
同时,总结了离子状水平的特征和光谱精细结构。
林和成[9]在研究了类氢离子时的电子自旋和轨道角动量,同时提出有关于氢离子和类氢离子的轨道能级的计算方法,同时,提出了一种氢离子计算方法,改善了氢类离子精细结构的理论计算。
弓斌耀[6]阐述了氢原子谱精细结构的规律和过渡规律。
在考虑相对论效应与自旋轨道之间的相互作用后,分析了精细结构中的过渡规则。
黄时中[2]等人计算36个类氢离子的电离能,并比较了实验值与量子力学相对误差之间的相对误差。
因此,获得了类氢离子的电离能的相对论计算。
1. 氢原子的光谱光谱学是研究原子结构的重要因素,在研究光谱的时候需要通过光谱仪,光源等情况进行分析。
1.1 玻尔的氢原子理论(1)定态假设:假设该原子是在一个稳定的状态,并具有所谓的静止状态的定义能量值。
当原子处于静止状态时,它既不能吸收能量也不能释放能量。

Br~(32+)离子1s~2ns-1s~2np态跃迁能和振子强度的理论计算本文介绍了我国原子与分子物理的研究现状和发展概况,阐明了高核电荷离子的性质、制备方法以及在相关学科领域的重要性。
以高核电荷离子Br32+为研究对象,应用全实加关联的方法计算了类锂体系Br32+离子1s2ns和1s2np(2≤n≤9)的非相对论总能量。
为了得到高精度的理论数据,将相对论效应和质量极化效应作为一阶微扰,对Br32+离子体系的能量进行一阶修正,与此同时还考虑了量子电动力学(QED)效应和高阶相对论效应对体系能量的贡献。
在确定了Br32+离子体系各能级总能量的基础上,计算出体系的电离能、跃迁能、跃迁波长和激发能;利用自旋-轨道相互作用(S-O)和自旋-其他轨道(S-O-O)相互作用算符的期待值得到了类锂体系Br32+离子1s2np态的精细结构劈裂。
根据量子亏损理论,计算了类锂体系Br32+离子1s2ns和1s2np两个态Rydberg系列的量子数亏损,并得到了对任意高激发态能量的理论预言。
本文还计算了类锂体系Br32+离子1s2ns-1s2n’p(2≤n≤9,3≤n’≤9)三种规范下的偶极跃迁振子强度,同时还对振子强度进行外推。
当任意初态确定,根据单通道量子亏损理论,可以完成从这一初态到其它分立态的所有可能允许的偶极跃迁振子强度的计算,还可以进行由这一初态到连续态的振子强度密度的理论研究,进而得到了整个体系的分立态间振子强度和分立态与连续态的振子强度密度的理论预言。
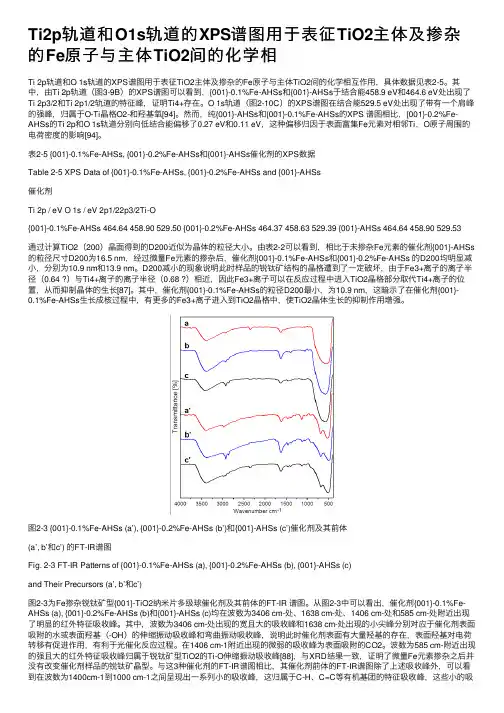
Ti2p轨道和O1s轨道的XPS谱图⽤于表征TiO2主体及掺杂的Fe原⼦与主体TiO2间的化学相Ti 2p轨道和O 1s轨道的XPS谱图⽤于表征TiO2主体及掺杂的Fe原⼦与主体TiO2间的化学相互作⽤,具体数据见表2-5。
其中,由Ti 2p轨道(图3-9B)的XPS谱图可以看到,{001}-0.1%Fe-AHSs和{001}-AHSs于结合能458.9 eV和464.6 eV处出现了Ti 2p3/2和Ti 2p1/2轨道的特征峰,证明Ti4+存在。
O 1s轨道(图2-10C)的XPS谱图在结合能529.5 eV处出现了带有⼀个肩峰的强峰,归属于O-Ti晶格O2-和羟基氧[94]。
然⽽,纯{001}-AHSs和{001}-0.1%Fe-AHSs的XPS 谱图相⽐,{001}-0.2%Fe-AHSs的Ti 2p和O 1s轨道分别向低结合能偏移了0.27 eV和0.11 eV,这种偏移归因于表⾯富集Fe元素对相邻Ti,O原⼦周围的电荷密度的影响[94]。
表2-5 {001}-0.1%Fe-AHSs, {001}-0.2%Fe-AHSs和{001}-AHSs催化剂的XPS数据Table 2-5 XPS Data of {001}-0.1%Fe-AHSs, {001}-0.2%Fe-AHSs and {001}-AHSs催化剂Ti 2p / eV O 1s / eV 2p1/22p3/2Ti-O{001}-0.1%Fe-AHSs 464.64 458.90 529.50 {001}-0.2%Fe-AHSs 464.37 458.63 529.39 {001}-AHSs 464.64 458.90 529.53通过计算TiO2(200)晶⾯得到的D200近似为晶体的粒径⼤⼩。
由表2-2可以看到,相⽐于未掺杂Fe元素的催化剂{001}-AHSs 的粒径尺⼨D200为16.5 nm,经过微量Fe元素的掺杂后,催化剂{001}-0.1%Fe-AHSs和{001}-0.2%Fe-AHSs 的D200均明显减⼩,分别为10.9 nm和13.9 nm。
二氧化钛能带机构和费米能级
二氧化钛(TiO2)是一种常见的半导体材料。
它的能带结构
主要由价带和导带组成。
在二氧化钛中,价带是最高能级的能带,包括由氧原子的2p
轨道和钛原子的3d轨道形成的能级。
导带是最低能级的能带,由钛原子的4s和3d轨道形成。
这两个能级之间存在能隙,也
就是禁带宽度,决定了二氧化钛的半导体特性。
费米能级是能带中被填充电子和未被填充电子之间分界处的能级。
在绝对零度下,费米能级位于填充电子的最高能级上。
根据能带填充原理,费米能级以下的能级被填充满电子,而费米能级以上的能级没有电子填充。
对于二氧化钛这样的半导体材料,费米能级的位置决定了材料的导电性质。
费米能级位于禁带中间时,材料是半导体。
费米能级在价带或导带上时,材料可能会表现出金属的导电性。
二价铁离子总磁矩二价铁离子总磁矩是指二价铁离子在外加磁场下所表现出的总磁性。
为了理解二价铁离子总磁矩的形成,我们需要先了解一些基本概念和原理。
一、基本概念1. 电子自旋:电子具有自旋角动量,可以看作是电子自身围绕轴心旋转所产生的现象。
电子自旋有两个取向,即自旋向上和自旋向下。
2. 电子轨道角动量:电子在原子核周围运动形成的轨道称为电子轨道。
电子轨道角动量是指电子在轨道运动时所具有的角动量。
3. 磁偶极矩:由于电荷的运动而产生的磁性称为磁偶极矩。
一个物体的磁偶极矩与其内部带正负相等、大小相等但方向相反的两个点电荷之间的距离和它们之间的连线垂直于这些点上。
4. 总磁矩:一个物体在外加磁场下所表现出来的总磁性称为总磁矩。
总磁力可以分为两部分,即轨道磁矩和自旋磁矩。
二、二价铁离子总磁矩的形成1. 轨道磁矩:二价铁离子的电子在原子核周围的轨道运动形成了电子轨道角动量,从而产生了轨道磁矩。
轨道磁矩的大小与电子轨道角动量成正比。
2. 自旋磁矩:二价铁离子的电子具有自旋,即自旋向上和自旋向下。
自旋向上和自旋向下的电子分别具有相反的自旋角动量,并且它们之间存在着相互作用。
这种相互作用使得自旋向上和自旋向下的电子在外加磁场下产生了自旋磁矩。
自旋磁矩的大小与电子自旋角动量成正比。
3. 总磁力:二价铁离子总共有5个d电子,其中4个是未配对电子。
未配对电子会产生额外的总轨道角动量和总自旋角动量。
根据洪特规则(Hund's rule),总轨道角动量和总自旋角动量取最大值,从而使得总磁力最大。
三、计算二价铁离子总磁矩的方法1. 轨道磁矩的计算:轨道磁矩的大小可以通过以下公式计算:μL = -√(L(L+1)) × μB其中,μL为轨道磁矩,L为电子轨道角动量量子数,μB为玻尔磁子。
2. 自旋磁矩的计算:自旋磁矩的大小可以通过以下公式计算:μS = -2 × √(S(S+1)) × μB其中,μS为自旋磁矩,S为电子自旋角动量量子数,μB为玻尔磁子。
二聚体系常数的计算方法
1 二聚体系常数的概念
二聚体系常数是指二价离子的结合能力的定量描述,它表示在一
定浓度条件下,一定量的离子可以形成一个二聚体。
根据不同的条件,可以分为弱电解质系常数、强电解质系常数等。
2 计算方法
1.弱电解质聚合常数
一般来说,弱电解质聚合常数容易计算,只需要将物质浓度和离
子常数代入其计算公式:
K=[(A+)×(B-) ]/[A]×[B]
其中K为聚合常数;A、B为所计算的不同离子,+(-)分别代表这
些离子的正负电荷;[A]和[B]分别表示他们的摩尔浓度。
2.强电解质聚合常数
强电解质聚合常数的计算略有不同,计算式如下:
K=([A+]2×[B-]2)/[A]×[B]
类似上述,K为聚合常数;A、B为所计算的不同离子,+(-)分别
代表这些离子的正负电荷;[A+]2、[B-]2分别表示强电解质所形成的
正负离子的平方;[A]和[B]分别表示他们的摩尔浓度。
3 总结
二聚体系常数反映离子结合能力的定量描述,可用于比较不同稀释溶液的离子结合能力。
二聚体系常数的计算方法主要有弱电解质系常数和强电解质系常数,计算公式分别如上所述。
二价钴离子自旋值1. 引言二价钴离子作为一种重要的过渡金属离子,在许多化学和物理领域中具有广泛的应用。
自旋值是描述物质自旋状态的重要参数,对于理解物质的性质和行为具有重要意义。
本文将详细介绍二价钴离子的基本性质、自旋值的定义和测量方法,以及二价钴离子自旋值的影响因素和应用。
2. 二价钴离子的基本性质2.1 原子结构和电子排布钴是一种过渡金属元素,其原子结构具有3d和4s电子层。
在二价钴离子中,一个电子从4s层跃迁到3d层,形成3d74s2的电子排布。
这种电子排布使得二价钴离子具有较高的自旋多重度。
2.2 离子的形成与性质二价钴离子通常通过失去一个电子形成,其离子半径较小,具有较高的化学活性。
二价钴离子在溶液中容易与其他离子形成配位键,形成稳定的配合物。
这些配合物的性质受到二价钴离子自旋状态的影响。
3. 自旋值的定义和测量方法3.1 自旋值的定义自旋值是描述物质自旋状态的重要参数,它表示物质自旋的净磁矩。
对于二价钴离子,其自旋值可以通过其电子排布和磁性性质进行计算。
3.2 自旋值的测量方法自旋值的测量方法主要有两种:实验测量和理论计算。
实验测量通常通过磁性测量仪进行,可以准确地测定物质的自旋值。
而理论计算则是基于量子力学和电子结构计算方法,可以对物质自旋值进行较为精确的计算。
4. 二价钴离子的自旋值4.1 实验测定通过实验测量,可以确定二价钴离子的自旋值。
实验测量的结果通常会受到实验条件、样品纯度等因素的影响。
因此,在实验测量过程中需要注意这些因素的控制,以确保结果的准确性。
4.2 理论计算基于量子力学和电子结构计算方法,可以对二价钴离子的自旋值进行理论计算。
这种计算方法可以较为准确地预测物质的自旋值,为实验研究提供理论支持。
5. 自旋值的影响因素5.1 配位环境二价钴离子在溶液中的配位环境对其自旋值有重要影响。
不同的配位体和配位环境会导致二价钴离子自旋值的改变。
这种改变通常是由于配位体对二价钴离子电子排布的干扰和影响所致。
锂二正离子的薛定谔方程
薛定谔方程公式:c1+c2=1c2。
薛定谔方程又称薛定谔波动方程,是由奥地利物理学家薛定谔提出的量子力学中的一个基本方程,也是量子力学的一个基本假定。
它是将物质波的概念和波动方程相结合建立的二阶偏微分方程,可描述微观粒子的运动,每个微观系统都有一个相应的薛定谔方程式,通过解方程可得到波函数的具体形式以及对应的能量,从而了解微观系统的性质。
薛定谔方程表明量子力学中,粒子以概率的方式出现,具有不确定性,宏观尺度下失效可忽略不计。
二价锂离子是丢失两个电子的一个结构,只有原子核和一个电子,所以它被称为“类氢离子”,这个结构的定态薛定谔方程的写法,在形式上和氢原子基本一致,只不过具体的原子核质量以及原子核的核电荷数Z的数字有所不同。
HΨ=EΨ,其中哈密顿算符H的形式和氢
原子一致。
tib2 晶格常数摘要:1.引言2.tib2 晶格常数的定义3.tib2 晶格常数的计算方法4.tib2 晶格常数的应用5.总结正文:1.引言晶格常数(Lattice constant)是描述晶体结构的重要参数,它反映了晶体内部原子或离子排列的周期性。
对于不同的晶体材料,其晶格常数会有所不同。
在此,我们将以tib2 晶体为例,介绍晶格常数的相关知识。
2.tib2 晶格常数的定义tib2 晶格常数是指在tib2 晶体结构中,相邻原子之间的距离。
具体来说,它是沿着晶格的对角线方向上的原子间距。
晶格常数通常用a、b、c 表示,分别对应晶体的三个晶格参数。
3.tib2 晶格常数的计算方法tib2 晶格常数的计算方法通常采用实验方法,如X 射线衍射(X-ray diffraction)和电子衍射(electron diffraction)等。
这些实验方法可以精确地测量出晶体内部原子的排列情况,从而计算出晶格常数。
此外,理论计算方法也可以用于预测tib2 晶格常数。
例如,密度泛函理论(density functional theory,DFT)是一种常用的计算方法,可以通过计算机模拟来预测晶格常数。
4.tib2 晶格常数的应用tib2 晶格常数在材料科学和工程领域具有广泛的应用,主要包括以下几个方面:(1)晶体结构分析:晶格常数是描述晶体结构的基本参数,通过测量晶格常数,可以了解晶体内部原子的排列方式,进而分析晶体的结构。
(2)材料性能预测:晶格常数与材料的力学性能、磁性能、电子性能等密切相关。
因此,通过计算晶格常数,可以预测材料的性能。
(3)材料制备:在材料制备过程中,通过控制晶格常数,可以实现对材料性能的调控。
例如,在半导体材料中,通过改变晶格常数,可以实现对材料带隙的调控。
5.总结tib2 晶格常数是描述tib2 晶体结构的重要参数,其计算方法包括实验方法和理论计算方法。