§第 13 讲 《对称分量法》
- 格式:pdf
- 大小:60.74 KB
- 文档页数:1

对称分量法(零序,正序,负序)的理解与计算1)求零序分量:把三个向量相加求和。
即A相不动,B相的原点平移到A相的顶端(箭头处),注意B相只是平移,不能转动。
同方法把C相的平移到B相的顶端。
此时作A相原点到C相顶端的向量(些时是箭头对箭头),这个向量就是三相向量之和.最后取此向量幅值的三分一,这就是零序分量的幅值,方向与此向量是一样的。
2)求正序分量:对原来三相向量图先作下面的处理:A相的不动,B相逆时针转120度,C 相顺时针转120度,因此得到新的向量图。
按上述方法把此向量图三相相加及取三分一,这就得到正序的A相,用A相向量的幅值按相差120度的方法分别画出B、C两相.这就得出了正序分量。
3)求负序分量:注意原向量图的处理方法与求正序时不一样。
A相的不动,B相顺时针转120度,C相逆时针转120度,因此得到新的向量图.下面的方法就与正序时一样了.对电机回路来说是三相三线线制,Ia+Ib+Ic=0,三相不对称时也成立;当Ia+Ib+Ic≠0时必有一相接地,对地有有漏电流;对三相四线制则为Ia+Ib+Ic+Io=0成立,只要无漏电,三相不对称时也成立;因此,零序电流通常作为漏电故障判断的参数。
负序电流则不同,其主要应用于三相三线的电机回路;在没有漏电的情况下(即Ia+Ib+Ic=0),三相不对称时也会产生负序电流;负序电流常作为电机故障判断;注意了:Ia+Ib+Ic=0与三相对称不是一回事;Ia+Ib+Ic=0时,三相仍可能不对称。
注意了:三相不平衡与零序电流不可混淆呀!三相不平衡时,不一定会有零序电流的;同样有零序电流时,三相仍可能为对称的.(这句话对吗?)前面好几位把两者混淆了吧!正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时,把三相的不对称分量分解成对称分量(正、负序)及同向的零序分量。
只要是三相系统,一般针对三相三线制的电机回路,就能分解出上述三个分量(有点象力的合成与分解,但很多情况下某个分量的数值为零)。

对称分量法(零序,正序,负序)的理解与计算对称分量法(零序,正序,负序)的理解与计算1)求零序分量:把三个向量相加求和。
即A相不动,B相的原点平移到A相的顶端(箭头处),注意B相只是平移,不能转动。
同方法把C相的平移到B相的顶端。
此时作A相原点到C相顶端的向量(些时是箭头对箭头),这个向量就是三相向量之和。
最后取此向量幅值的三分一,这就是零序分量的幅值,方向与此向量是一样的。
2)求正序分量:对原来三相向量图先作下面的处理:A相的不动,B相逆时针转120度,C 相顺时针转120度,因此得到新的向量图。
按上述方法把此向量图三相相加及取三分一,这就得到正序的A相,用A相向量的幅值按相差120度的方法分别画出B、C两相。
这就得出了正序分量。
3)求负序分量:注意原向量图的处理方法与求正序时不一样。
A 相的不动,B相顺时针转120度,C相逆时针转120度,因此得到新的向量图。
下面的方法就与正序时一样了。
对电机回路来说是三相三线线制,Ia+Ib+Ic=0,三相不对称时也成立;当Ia+Ib+Ic≠0时必有一相接地,对地有有漏电流;对三相四线制则为Ia+Ib+Ic+Io=0成立,只要无漏电,三相不对称时也成立;因此,零序电流通常作为漏电故障判断的参数。
负序电流则不同,其主要应用于三相三线的电机回路;在没有漏电的情况下(即Ia+Ib+Ic=0),三相不对称时也会产生负序电流;负序电流常作为电机故障判断;注意了:Ia+Ib+Ic=0与三相对称不是一回事;Ia+Ib+Ic=0时,三相仍可能不对称。
注意了:三相不平衡与零序电流不可混淆呀!三相不平衡时,不一定会有零序电流的;同样有零序电流时,三相仍可能为对称的。
(这句话对吗?)前面好几位把两者混淆了吧!正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时,把三相的不对称分量分解成对称分量(正、负序)及同向的零序分量。
只要是三相系统,一般针对三相三线制的电机回路,就能分解出上述三个分量(有点象力的合成与分解,但很多情况下某个分量的数值为零)。



对称分量法公式摘要:一、对称分量法简介1.对称分量法的概念2.对称分量法在工程中的应用二、对称分量法公式推导1.基本电路分析2.对称分量法的推导过程3.对称分量法公式三、对称分量法应用实例1.三相电路分析2.发电机和变压器分析3.其他应用场景四、对称分量法的优缺点1.优点2.缺点正文:一、对称分量法简介对称分量法是一种电路分析方法,主要用于解决不对称三相电路的问题。
该方法将三相电路分解为三个独立的单相电路,通过对每个单相电路的分析,可以得到三相电路中各相的电流和电压。
对称分量法广泛应用于电力系统、自动化控制等领域。
二、对称分量法公式推导1.基本电路分析首先,我们分析一个简单的不对称三相电路,包含三个相电压U1、U2、U3 和一个中性线N。
我们用矢量表示电压和电流:U1、U2、U3 和I1、I2、I3。
2.对称分量法的推导过程为了方便分析,我们将电压和电流分解为正序和负序两个分量。
正序分量表示三相电压和电流的平衡部分,负序分量表示三相电压和电流的不平衡部分。
正序分量和负序分量的关系如下:U1p = U1 + U2 + U3I1p = I1 + I2 + I3U1n = U1 - U2 - U3I1n = I1 - I2 - I3其中,U1p、I1p 表示正序分量的电压和电流,U1n、I1n 表示负序分量的电压和电流。
3.对称分量法公式根据对称分量法,我们可以得到以下公式:U1p = U1 + jU2 + jU3I1p = I1 + jI2 + jI3U1n = U1 - jU2 - jU3I1n = I1 - jI2 - jI3其中,j 表示虚数单位。
三、对称分量法应用实例1.三相电路分析通过对称分量法,我们可以将复杂的不对称三相电路分解为三个简单的单相电路。
这样,我们可以分别分析每个单相电路,从而简化电路分析过程。
2.发电机和变压器分析对称分量法广泛应用于发电机和变压器的分析。
通过分解发电机和变压器的不对称电流和电压,我们可以了解设备的运行状态,及时发现故障,保证电力系统的稳定运行。
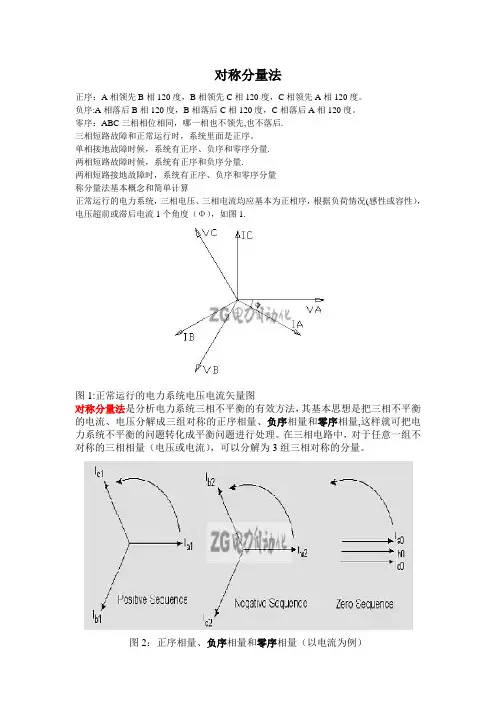
对称分量法正序:A相领先B相120度,B相领先C相120度,C相领先A相120度。
负序:A相落后B相120度,B相落后C相120度,C相落后A相120度。
零序:ABC三相相位相同,哪一相也不领先,也不落后.三相短路故障和正常运行时,系统里面是正序。
单相接地故障时候,系统有正序、负序和零序分量.两相短路故障时候,系统有正序和负序分量.两相短路接地故障时,系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统,三相电压、三相电流均应基本为正相序,根据负荷情况(感性或容性),电压超前或滞后电流1个角度(Φ),如图1.图1:正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法,其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量,这样就可把电力系统不平衡的问题转化成平衡问题进行处理。
在三相电路中,对于任意一组不对称的三相相量(电压或电流),可以分解为3组三相对称的分量。
图2:正序相量、负序相量和零序相量(以电流为例)当选择A相作为基准相时,三相相量与其对称分量之间的关系(如电流)为:IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1 IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量:Ib1=α2 Ia1 ,Ic1=αIa1对于负序分量:Ib2=αIa2 ,Ic2=α2Ia2对于零序分量:Ia0= Ib0 = Ic0式中,α为运算子,α=1∠120°有α2=1∠240°,α3=1,α+α2+1=0由各相电流求电流序分量:I1=Ia1= 1/3(IA +αIB +α2 IC)I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义(方法)求解。

对称分量法(零序,正序,负序)的理解与计算对称分量法(零序,正序,负序)的理解与计算1)求零序分量:把三个向量相加求和。
即A相不动,B相的原点平移到A相的顶端(箭头处),注意B相只是平移,不能转动。
同方法把C相的平移到B相的顶端。
此时作A相原点到C相顶端的向量(些时是箭头对箭头),这个向量就是三相向量之和。
最后取此向量幅值的三分一,这就是零序分量的幅值,方向与此向量是一样的。
2)求正序分量:对原来三相向量图先作下面的处理:A相的不动,B相逆时针转120度,C相顺时针转120度,因此得到新的向量图。
按上述方法把此向量图三相相加及取三分一,这就得到正序的A相,用A相向量的幅值按相差120度的方法分别画出B、C两相。
这就得出了正序分量。
3)求负序分量:注意原向量图的处理方法与求正序时不一样。
A相的不动,B 相顺时针转120度,C相逆时针转120度,因此得到新的向量图。
下面的方法就与正序时一样了。
对电机回路来说是三相三线线制,Ia+Ib+Ic=0,三相不对称时也成立;当Ia+Ib+Ic≠0时必有一相接地,对地有有漏电流;对三相四线制则为Ia+Ib+Ic+Io=0成立,只要无漏电,三相不对称时也成立;因此,零序电流通常作为漏电故障判断的参数。
负序电流则不同,其主要应用于三相三线的电机回路;在没有漏电的情况下(即Ia+Ib+Ic=0),三相不对称时也会产生负序电流;负序电流常作为电机故障判断;注意了:Ia+Ib+Ic=0与三相对称不是一回事;Ia+Ib+Ic=0时,三相仍可能不对称。
注意了:三相不平衡与零序电流不可混淆呀!三相不平衡时,不一定会有零序电流的;同样有零序电流时,三相仍可能为对称的。
(这句话对吗?)前面好几位把两者混淆了吧!正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时,把三相的不对称分量分解成对称分量(正、负序)及同向的零序分量。
只要是三相系统,一般针对三相三线制的电机回路,就能分解出上述三个分量(有点象力的合成与分解,但很多情况下某个分量的数值为零)。

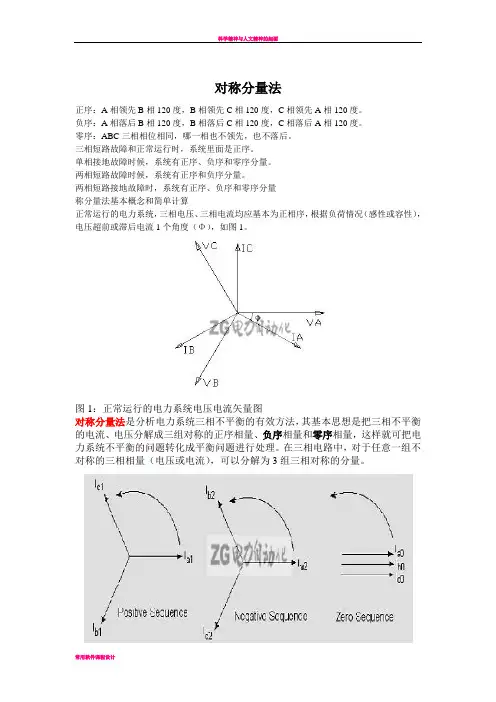
对称分量法正序:A相领先B相120度,B相领先C相120度,C相领先A相120度。
负序:A相落后B相120度,B相落后C相120度,C相落后A相120度。
零序:ABC三相相位相同,哪一相也不领先,也不落后。
三相短路故障和正常运行时,系统里面是正序。
单相接地故障时候,系统有正序、负序和零序分量。
两相短路故障时候,系统有正序和负序分量。
两相短路接地故障时,系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统,三相电压、三相电流均应基本为正相序,根据负荷情况(感性或容性),电压超前或滞后电流1个角度(Φ),如图1。
图1:正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法,其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量,这样就可把电力系统不平衡的问题转化成平衡问题进行处理。
在三相电路中,对于任意一组不对称的三相相量(电压或电流),可以分解为3组三相对称的分量。
图2:正序相量、负序相量和零序相量(以电流为例)当选择A相作为基准相时,三相相量与其对称分量之间的关系(如电流)为:IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量:Ib1=α2 Ia1 ,Ic1=αIa1对于负序分量:Ib2=αIa2 ,Ic2=α2Ia2对于零序分量:Ia0= Ib0 = Ic0式中,α为运算子,α=1∠120°有α2=1∠240°, α3=1, α+α2+1=0由各相电流求电流序分量:I1=Ia1= 1/3(IA +αIB +α2 IC)I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义(方法)求解。


对称分量法的主要内容对称分量法,听起来是不是有点高大上?其实它就是一种用来分析和处理电力系统中不对称故障的技术。
嗯,别担心,这不是那些复杂到让你头疼的数学公式,也不是只有工程师才懂的神秘语言。
它就像是给电力系统做了个“大扫除”,把那些乱七八糟的电流、电压“整理”得清清楚楚。
怎么个整理法呢?说白了,就是把复杂的三相电力系统分解成几个简单的部分,这样一来,分析起来就轻松多了。
想象一下,你有三个颜色的球——红、绿、蓝。
原本它们在一起混杂,看上去有点乱,想要搞清楚每个颜色球的具体情况,怎么办?简单,把这些球分开,单独看看每个颜色是怎么回事。
对,就是这个道理。
对称分量法的核心思想,就是把三相电流或者电压分解成三种分量:正序分量、负序分量和零序分量。
说起来这三个名字好像有点抽象,但其实每个都很有“特色”。
正序分量,简单来说,就是最正常的情况,大家都按秩序排好队,电流、电压各自稳定。
这就像是一个小小的电力世界,秩序井然,三相电压的幅值相等,角度相差120度,一切都挺好,没啥问题。
这个分量是我们常见的正常工作状态,整个系统运行得好好的,啥毛病都没有。
正序分量就好比一个团队里,大家都很努力地工作,目标一致,大家都心往一处想。
然后是负序分量,这个嘛,就有点不太对劲了。
负序分量代表的就是一种不平衡状态,电流、电压的幅值虽然差不多,但它们的相位角有点“调皮”,不像正序分量那样整齐划一。
这就像是一个团体里,有人开始偏离节奏,开始不太配合,有点“不务正业”的感觉。
负序分量往往出现在电力系统出现故障的时候,比如电机偏心,负载不平衡,这些都可能让电流或电压变得不对称,影响系统的稳定性。
零序分量嘛,听起来就像是“零零碎碎”的东西。
它代表了系统中存在的一些特殊情况,比如三相电压或者电流不完全对称,可能是某个相的电流出现了异常,或者系统有接地故障时,零序分量就会显现出来。
简单来说,零序分量就像是你在做饭时,发现锅里多了一点油,虽然不多,但也不能忽视。
§第13讲 《对称分量法》
一、教学目标 对称分量法原理,它是分析、计算不对称短路的基础。
相量的旋转因子及由旋转因子组成的变换矩阵,它是具体进行对称量与不对称量之间互换的计算因子。
二、教学重点
对称概念;对称分量法;不对称量;对称分量;正序量概念、负序量概念、零序量概念;旋转因子;不对称量与对称分量之间的变换矩阵;不对称量与对称分量之间α=e j 1200的互换计算;变换矩阵表示了不对称量与对称分量之间的关系。
三、教学难点
对称分量法的数学意义和物理意义
四、教学内容和要点 ⑴ 首先以电压或电流为例搞清什么是正序、负序、零序对称量。
对称是三相量数值相等,相位差相同。
正序量相量的顺序是a 、b 、c 按顺时针方向排序。
负序是a 、b 、c 按逆时针方向排序。
零序,a 、b 、c 相位差是00(或3600)。
旋转因子表示相量按正方向旋转120α=e j 12000,
和其关系 ,10
α31=2++=αα⑵ 三相不对称量可以唯一地用一组对称分量合成,反之,三相不对称量可以唯一地 分解成一组对称分量,合成和分解通过变换矩阵T 及其逆矩阵T −1
来实现。
他们既适用于电压变换也适用于电流变换。
记住变换矩阵
五、采用的教学方法和手段
教学方法(如:讲述法、讨论法、实验法等):讲述法
教学手段(如:挂图、模型、仪器、投影、幻灯等):板书。
对称分量法(零序,正序,负序)的理解与计算1)求零序分量:把三个向量相加求和。
即A相不动,B相的原点平移到A相的顶端(箭头处),注意B相只是平移,不能转动。
同方法把C相的平移到B相的顶端。
此时作A相原点到C相顶端的向量(些时是箭头对箭头),这个向量就是三相向量之和。
最后取此向量幅值的三分一,这就是零序分量的幅值,方向与此向量是一样的。
2)求正序分量:对原来三相向量图先作下面的处理:A相的不动,B相逆时针转120度,C 相顺时针转120度,因此得到新的向量图。
按上述方法把此向量图三相相加及取三分一,这就得到正序的A相,用A相向量的幅值按相差120度的方法分别画出B、C两相。
这就得出了正序分量。
3)求负序分量:注意原向量图的处理方法与求正序时不一样。
A相的不动,B相顺时针转120度,C相逆时针转120度,因此得到新的向量图。
下面的方法就与正序时一样了。
对电机回路来说是三相三线线制,Ia+Ib+Ic=0,三相不对称时也成立;当Ia+Ib+Ic≠0时必有一相接地,对地有有漏电流;对三相四线制则为Ia+Ib+Ic+Io=0成立,只要无漏电,三相不对称时也成立;因此,零序电流通常作为漏电故障判断的参数。
负序电流则不同,其主要应用于三相三线的电机回路;在没有漏电的情况下(即Ia+Ib+Ic=0),三相不对称时也会产生负序电流;负序电流常作为电机故障判断;注意了:Ia+Ib+Ic=0与三相对称不是一回事;Ia+Ib+Ic=0时,三相仍可能不对称。
注意了:三相不平衡与零序电流不可混淆呀!三相不平衡时,不一定会有零序电流的;同样有零序电流时,三相仍可能为对称的。
(这句话对吗?)前面好几位把两者混淆了吧!正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时,把三相的不对称分量分解成对称分量(正、负序)及同向的零序分量。
只要是三相系统,一般针对三相三线制的电机回路,就能分解出上述三个分量(有点象力的合成与分解,但很多情况下某个分量的数值为零)。
第一节对称分量法图4—1(a)、(b)、(c)表示三组对称的三相相量。
第一组相量Fa(1)、相量F b(1). 相量Fc(1),幅值相等。
相位为“a 超前b 120度,b超前c 120度,称为正序;第二组相量Fa(2). 相量F b(2)相量.Fc(2),幅值相等,相序与正序相反,称为负序;第三组相量Fa(0)、相量.F b(0)、相量Fc(0),幅值和相位均相同,称为零序。
在图4—1(d)中将每一组的带下标a的三个相量合成为Fa,,带下标b的合成为Fb,,带下标c的合成为F是三个小对称的相量,即三组对称的相量合成得相量Fa、Fb、Fc是三个不对称的相量。
写成数学表达式为:由于每一组是对称的,固有下列关系:将式(4-2)代入式(4-1)可得:此式表示上述三个不对称相量和三个对称相量中a相量的关系。
其矩阵形式为:或简写为式(4-4)和式(4-5)说明三相对称相量合成得三个不对称相量。
其逆关系为:或简写为式(4—6)和(4—7)说明由三个不对称的相量可以唯一地分解成三组对称的相量(即对称分量);正序分量、负序分员和不序分量。
实际上,式(4—4)和(4—6)表示三个对称相量Fa、Fb、Fc和另外三个相量Fa(1)、 Fa(2)、 Fa(0)之间的线性变换关系。
如果电力系统某处发生不对称短路,尽管除短路点外三相系统的元件参数都是对称的,三相电路的电流和电压的基频分量都变成不对称的相量。
将式(4—6)的变换关系应用于基频电流(或电压),则有即将三相不对称电流(以后略去“基频”二字)Ia、Ib、Ic经过线性变换后,可分解成三组对称的电流。
即a相电流Ia分解成Ia(1)、Ia(2)、Ia(0),b相电流Ib分解成Ib(1)、Ib(2)、Ib(0),c相电流Ic分解成Ic(1)、Ic(2)、Ic(0)。
其中Ia(1)、Ib(1)、Ic(1)一组对称的相量,称为正序分量电流;Ia(2)、Ib(2)、Ic(2)也是一组对称的相量。
§第13讲 《对称分量法》
一、教学目标 对称分量法原理,它是分析、计算不对称短路的基础。
相量的旋转因子及由旋转因子组成的变换矩阵,它是具体进行对称量与不对称量之间互换的计算因子。
二、教学重点
对称概念;对称分量法;不对称量;对称分量;正序量概念、负序量概念、零序量概念;旋转因子;不对称量与对称分量之间的变换矩阵;不对称量与对称分量之间α=e j 1200的互换计算;变换矩阵表示了不对称量与对称分量之间的关系。
三、教学难点
对称分量法的数学意义和物理意义
四、教学内容和要点 ⑴ 首先以电压或电流为例搞清什么是正序、负序、零序对称量。
对称是三相量数值相等,相位差相同。
正序量相量的顺序是a 、b 、c 按顺时针方向排序。
负序是a 、b 、c 按逆时针方向排序。
零序,a 、b 、c 相位差是00(或3600)。
旋转因子表示相量按正方向旋转120α=e j 12000,
和其关系 ,10
α31=2++=αα⑵ 三相不对称量可以唯一地用一组对称分量合成,反之,三相不对称量可以唯一地 分解成一组对称分量,合成和分解通过变换矩阵T 及其逆矩阵T −1
来实现。
他们既适用于电压变换也适用于电流变换。
记住变换矩阵
五、采用的教学方法和手段
教学方法(如:讲述法、讨论法、实验法等):讲述法
教学手段(如:挂图、模型、仪器、投影、幻灯等):板书。