EXCEL 制作正态分布曲线图

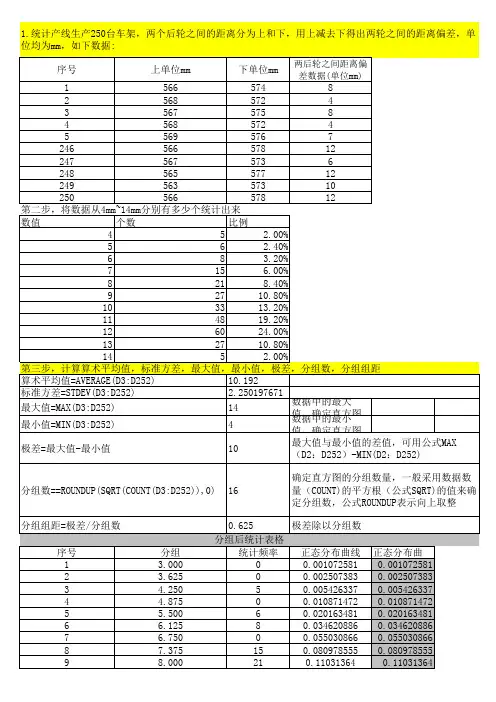
第四步，制作直方图：用频率来实现直方图第五步，修整直方图：1.将X轴中用分组数据来表示-单击柱形图空白区域右键，选择源数据，选择系列，点击分类X轴标志，选择单元格B276：B294 确定即可；第六步，制作正态分布图获取正态分布概念密度，正态分布概率密度正态分布函数“NORMDIST”获取。

在这里是以分组边界值为“X”来计算：Mean=AVERAGE(A:A)(数据算术平均）Standard_dev=STDEV(A:A)(数据的标准方差）Cumulative=0(概率密度函数）1.在正态分布曲线单元格下插入函数NORMDIST，函数参数中的数值栏表示用于计算正态分布函数值的区间点，即“分组”单元格下的数据，算术平均值用函数公式计算，标准方差用函数公式计算，返回累计分布函数用数字1表示TRUE，数字0表示FALSE返回的是概率密度函数，见下图2.在朝下填充中，要注意，函数的参数改变的是“数值”栏，算术平均值、标准方差、返回的累计函数分布是不变的，因此相应的用公式计算的参数中所引用的单元格是不变的，即算术平均值AVERAGE(D3：D252）不变，标准方差STDEV(D3：D252）不变，返回的函数逻辑值0不变。

第七步，绘制正态分布曲线图。

正态分布N（μ，σ2），已经将μ值10.192，σ的平方即标准方差2.250197671计算得出，据此绘制正态分布曲线图。

1.在直方图中，点击源数据，选择系列，点击添加，选择数据单元格即D276：D2942.由于直方图与正态分布在同一张图中数据差距太大，导致正态曲线图数据太小，不易选择。

可以选择直方图，右键数据系列格式中，坐标轴绘制在“次坐标轴”，这样突出显示的就是正态分布曲线和数据点，再将正态分布曲线及其数据点“数据系列格式”中用突出的颜色和增加粗细表示出来，然后再将直方图调整回“主坐标轴”，这样就比较容易看清曲线图中的数据点，选择之后“正态分布曲线”数据栏显示为被选中状态。

引用用Excel函数画曲线的方法1．用Excel函数画曲线图的一般方法因为Excel有强大的计算功能，而且有数据填充柄这个有力的工具，所以，绘制曲线还是十分方便的。

用Excel画曲线的最大优点是不失真。

大体步骤是这样的：⑴用“开始”→“程序”→“Microsoft office”→”Excel”,以进入Excel窗口。

再考虑画曲线，为此：⑵在A1 和A2单元格输入自变量的两个最低取值，并用填充柄把其它取值自动填入；⑶在B列输入与A列自变量对应的数据或计算结果。

有三种方法输入：第一种方法是手工逐项输入的方法，这种方法适合无确定数字规律的数据：例如日产量或月销售量等；第二种方法是手工输入计算公式法：这种方法适合在Excel的函数中没有列入粘贴函数的情况，例如，计算Y=3X^2时，没有现成的函数可用，就必须自己键入公式后，再进行计算；第三种方法是利用Excel 中的函数的方法，因为在Excel中提供了大量的内部预定义的公式，包括常用函数、数学和三角函数、统计函数、财务函数、文本函数等等。

怎样用手工输入计算公式和怎样利用Excel的函数直接得出计算结果，下面将分别以例题的形式予以说明；⑷开始画曲线：同时选择A列和B列的数据→“插入”→“图表”→这时出现如下图所示的图表向导:选“XY散点图”→在“子图表类型”中选择如图所选择的曲线形式→再点击下面的‘按下不放可查看示例’钮，以查看曲线的形状→“下一步”→选“系列产生在列”→“下一步”→“标题”（输入本图表的名称）→“坐标”（是否默认或取消图中的X轴和Y轴数据）→“网络线”（决定是否要网格线）→“下一步”后，图形就完成了；⑸自定义绘图区格式：因为在Excel工作表上的曲线底色是灰色的，线条的类型（如连线、点线等）也不一定满足需要，为此，可右击这个图，选“绘图区格式”→“自定义”→“样式”（选择线条样式）→“颜色”（如果是准备将这个曲线用在Word上，应该选择白色）→“粗细”（选择线条的粗细）。

excel正态分布曲线正态分布曲线也称为高斯分布曲线，是一种非常重要的连续概率分布，在统计学和科学研究中广泛应用。

它的形状呈钟形，且左右对称。

正态分布曲线是自然界中许多现象的表现形式，比如身高、体重、智商、经济收入等等。

在Excel中，我们可以使用NORM.DIST函数来计算正态分布曲线的概率值。

在本文中，我们将介绍如何绘制正态分布曲线以及如何使用Excel来计算正态分布概率值。

一、正态分布曲线的特点正态分布曲线的特点如下：1.左右对称：对于任意一组数据，正态分布曲线的左半部分和右半部分是对称的。

左右对称是由于正态分布曲线的数学定义，即所有点到均值的距离相等，且呈正态分布。

2.峰值处概率最大：正态分布曲线在均值处有一个峰值，该点处的概率值最大。

在峰值两侧，概率值逐渐减小。

正态分布曲线的峰值位于均值处，峰值左右的两个临界点分别位于均值两侧一个标准差的距离处。

3.形状具有稳定性：正态分布曲线的形状是固定的，无论均值或标准差如何变化，曲线的形状不变。

这就使得正态分布曲线成为一种非常重要的概率分布。

二、绘制正态分布曲线在Excel中，我们可以使用以下步骤来绘制正态分布曲线：1.打开Excel，新建一个工作簿。

2.输入以下数据：-A1单元格：均值（μ）-A2单元格：标准差（σ）-A3单元格：步长（从μ-3σ到μ+3σ，每隔0.1σ取一个值）3.在B3单元格中，输入以下公式：=NORM.DIST(A3,$A$1,$A$2,FALSE)。

这个公式中，A3是一个变量，表示横坐标值，$A$1和$A$2是固定值，分别表示均值和标准差。

FALSE 表示概率分布累积函数的形式，即对每个横坐标值分别计算它对应的纵坐标值。

4.复制B3单元格公式，从B4单元格到B61单元格。

5.选中A1单元格到B61单元格，然后选择插入散点图。

6.点击散点图右侧的加号，选择趋势线，然后选择添加趋势线。

7.在趋势线中，选择加权多项式趋势线，调整阶数为6，然后勾选显示方程和R平方值。

excel标准正态分布表一、概述在数据分析中，标准正态分布是一个非常重要的分布，它在许多领域都有着广泛的应用。

为了方便用户在Excel中进行标准正态分布的计算和查询，本文将介绍如何使用Excel制作标准正态分布表。

二、制作方法1.打开Excel，创建一个新的工作表。

2.在A1单元格中输入“标准正态分布表”，并设置适当的字体和颜色。

3.在B1单元格输入“μ”，在C1单元格输入“σ”。

其中μ是正态分布的均值，σ是正态分布的标准差。

4.从B2到Bn单元格依次输入-3、-2、-1、0、1、2、3等值的μ。

5.从C2到Cn单元格分别输入相应的σ值，例如0.05、0.025、0.01等。

6.将鼠标放在B10单元格上，点击“公式”菜单，选择“定义名称”。

在弹出的对话框中输入名称，如“norm_table”，并选择A2:C10区域。

7.在D1单元格输入“z”，并在D2单元格输入“=norm_table(μ,σ)”。

通过拖动填充柄，将D2单元格的公式应用到D列的其他单元格。

8.在E列和F列分别输入变量x和对应的概率值p。

可以使用D列的函数来计算每个x对应的p值。

9.调整列宽和行高，使表格更加美观。

三、使用方法1.在Excel中打开标准正态分布表，可以在B1:F1区域看到整个表格。

2.在需要使用标准正态分布的地方输入变量x的值，然后在对应的位置查找p值。

例如，在B3单元格输入x值“0.4”，然后在F3单元格即可找到对应的p 值。

3.如果需要计算某个概率下的x值，可以使用D列的函数来查找对应的μ和σ值，再使用B列的函数来查找对应的x值。

4.如果需要制作更复杂的数据表格，可以根据需要调整表格的格式和内容。

总之，Excel标准正态分布表是一个非常实用的工具，可以帮助用户在数据分析中快速查找标准正态分布的概率和对应的x值。

通过掌握制作和使用方法，可以更好地利用Excel进行数据分析和管理。

excel画正态分布曲线图正态分布是一种被广泛应用的概率分布，它的概率密度函数是一个标准的钟形曲线，它的简称为NDF(Normal Distribution Function)，或者叫作正态分布曲线。

正态分布在做实验中经常使用，但人们不得不用许多繁琐的统计学公式来绘制出正态分布曲线。

为了使用更简便的方法来绘制正态分布曲线，本文将介绍如何使用微软的Excel构建正态分布曲线图。

首先，需要准备一份Excel表格，将某一维度的分布曲线数据记录在一列中。

这里以“height”（身高）为例，在第一列的表格中，列出人的身高（以厘米为单位），在第二列的表格中，记录身高的频数（以人数为单位）。

接下来，在Excel中选择插入“图表”，选择“线形图”，把第一列的数据作为图表的X轴，第二列的数据作为图表的Y轴。

然后，在图表右上角的菜单中，点击“选项”，勾选“折线”并且把它改为“曲线”，当把曲线拖动到正常位置时，图表就出来了。

最后，可以给正态分布曲线图添加标题和比例尺，使其更加易于理解。

正态分布曲线图主要用于表示一组数据的分布特征。

例如，可以用正态分布曲线图来表示全国人口的年龄分布情况，或是某类测试成绩的分布特征，或是市场消费行为的变化情况。

另外，正态分布曲线图也可以用于比较两个不同维度的数据分布特征，从而更好地表现出这些数据之间的相关性。

正态分布曲线图被广泛应用于商业决策分析、统计学、有限元素分析等领域中，可以帮助人们对数据的变化趋势进行更加客观的分析，从而准确地了解现象背后的规律性。

使用Excel绘制正态分布曲线图不但简单易操作，而且能够获得较为准确的曲线图，因此得到了广泛的应用。

以上就是本文关于如何使用Excel画正态分布曲线图的介绍，希望读者通过本文的介绍，能够对Excel构建正态分布曲线图有一个较为完整的了解，可以灵活运用Excel技术来解决一些数据处理问题。

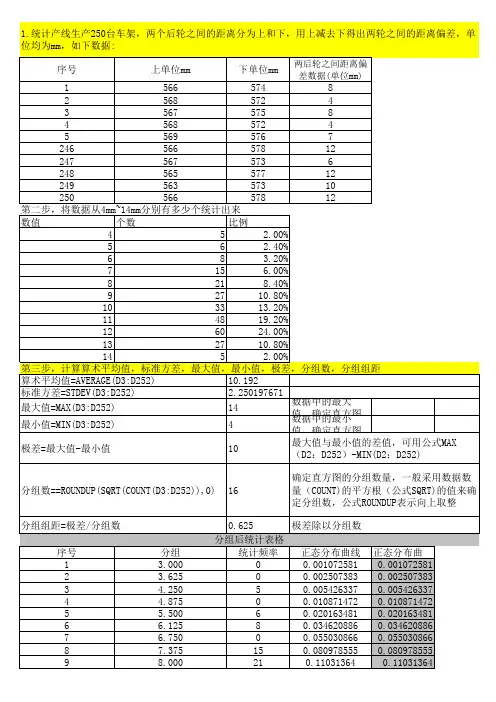
第四步，制作直方图：用频率来实现直方图第五步，修整直方图：1.将X轴中用分组数据来表示-单击柱形图空白区域右键，选择源数据，选择系列，点击分类X轴标志，选择单元格B276：B294 确定即可；第六步，制作正态分布图获取正态分布概念密度，正态分布概率密度正态分布函数“NORMDIST”获取。

在这里是以分组边界值为“X”来计算：Mean=AVERAGE(A:A)(数据算术平均）Standard_dev=STDEV(A:A)(数据的标准方差）Cumulative=0(概率密度函数）1.在正态分布曲线单元格下插入函数NORMDIST，函数参数中的数值栏表示用于计算正态分布函数值的区间点，即“分组”单元格下的数据，算术平均值用函数公式计算，标准方差用函数公式计算，返回累计分布函数用数字1表示TRUE，数字0表示FALSE返回的是概率密度函数，见下图2.在朝下填充中，要注意，函数的参数改变的是“数值”栏，算术平均值、标准方差、返回的累计函数分布是不变的，因此相应的用公式计算的参数中所引用的单元格是不变的，即算术平均值AVERAGE(D3：D252）不变，标准方差STDEV(D3：D252）不变，返回的函数逻辑值0不变。

第七步，绘制正态分布曲线图。

正态分布N（μ，σ2），已经将μ值10.192，σ的平方即标准方差2.250197671计算得出，据此绘制正态分布曲线图。

1.在直方图中，点击源数据，选择系列，点击添加，选择数据单元格即D276：D2942.由于直方图与正态分布在同一张图中数据差距太大，导致正态曲线图数据太小，不易选择。

可以选择直方图，右键数据系列格式中，坐标轴绘制在“次坐标轴”，这样突出显示的就是正态分布曲线和数据点，再将正态分布曲线及其数据点“数据系列格式”中用突出的颜色和增加粗细表示出来，然后再将直方图调整回“主坐标轴”，这样就比较容易看清曲线图中的数据点，选择之后“正态分布曲线”数据栏显示为被选中状态。

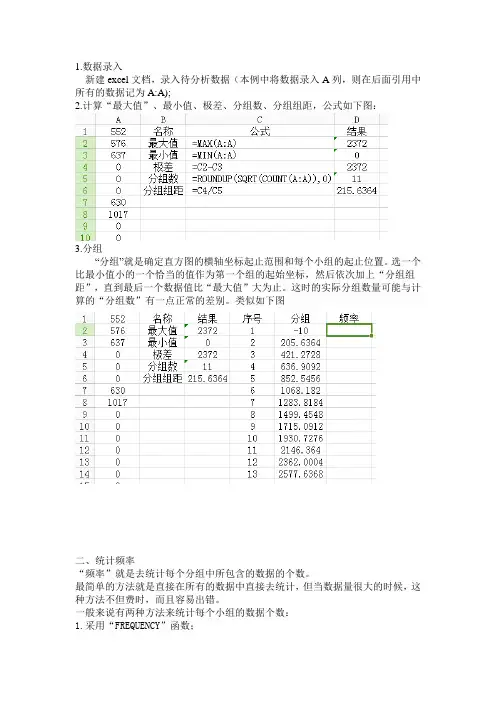
1.数据录入新建excel文档，录入待分析数据（本例中将数据录入A列，则在后面引用中所有的数据记为A:A);2.计算“最大值”、最小值、极差、分组数、分组组距，公式如下图：3.分组“分组”就是确定直方图的横轴坐标起止范围和每个小组的起止位置。

选一个比最小值小的一个恰当的值作为第一个组的起始坐标，然后依次加上“分组组距”，直到最后一个数据值比“最大值”大为止。

这时的实际分组数量可能与计算的“分组数”有一点正常的差别。

类似如下图二、统计频率“频率”就是去统计每个分组中所包含的数据的个数。

最简单的方法就是直接在所有的数据中直接去统计，但当数据量很大的时候，这种方法不但费时，而且容易出错。

一般来说有两种方法来统计每个小组的数据个数：1.采用“FREQUENCY”函数；2.采用“COUNT IF”让后再去相减。

这里介绍的是“FREQUENCY”函数方法：“Date_array”：是选取要统计的数据源，就是选择原始数据的范围；“Bins_array”：是选取直方图分组的数据源，就是选择分组数据的范围；生成“FREQUENCY”函数公式组，步骤如下：1. 先选中将要统计直方图每个子组中数据数量的区域2.再按“F2”健，进入到“编辑”状态再同时按住“Ctrl”和“Shift”两个键，再按“回车Enter”键，最后三键同时松开，大功告成！三、获取正态分布概率密度正态分布概率密度正态分布函数“NOR MDIST”获取。

在这里是以分组边界值为“X”来计算：Mean=AVERAGE(A:A)(数据算术平均）Standard_dev=STDEV(A:A)(数据的标准方差）Cumulative=0(概率密度函数）向下填充四、制作正态分布图1、选中统计好的折线图每个小组的分布概率密度，用折线图来完成正态分布图；2、选中正态分布概率密度列下所有数据（I2：I14），插入——图标——折线图，3、选好图表类型及配色方案后，单击“下一步”，进入“源数据”对话框，如图4、单击框图上“系列”菜单5、单击“添加”系列，新建系列二，如图6、在系列名称点击框选图标，在表格中选取G1单元格，其自动将“频率”转换成代码，再点击框选图标，返回源数据对话框7、然后在系列“值”栏，清除数据={1}后点击框选图标，在表格中选中频率下所有数据（G2：G14),8、再返回源数据对话框，可以看到原系列二已更名为频率9、单击系列1，将其名称更换为“正态分布概率密度”，即在选中系列1后10、在名称栏中点击框选图标，在表格中选中“I1”单元格后返回“源数据对话框”，11、在分类X轴标志栏，点击框选图标，在表格中选中分组列下所有数据（F2：F14),返回对话框，可以看到对话框中图表横轴发生变化12、然后单击“下一步’,进入图表选项对话框，在标题菜单的“图表标题”中输入“正态分布概率密度曲线”，在分类x轴中输入“分组”，在数据Y轴中输入“概率密度”，如图13、单击完成，图表绘制完成。

excel 正态分布曲线
Excel中如何绘制正态分布曲线？正态分布是一种重要的概率分布，广泛应用于统计学、金融学、经济学、医学等领域。

Excel 作为强大的数据处理工具，可以方便地绘制正态分布曲线。

首先，在Excel中输入数据，可以使用NORM.DIST函数计算随机变量X的概率密度函数值。

NORM.DIST函数的语法为：
NORM.DIST(x, mean, standard_dev, cumulative)，其中x表示要计算概率密度函数值的随机变量，mean表示随机变量X的均值，standard_dev表示随机变量X的标准差，cumulative表示是否计算累积分布函数值。

例如，在单元格A1中输入
=NORM.DIST(0,1,1,FALSE)，即可计算X=0处的概率密度函数值。

然后，在Excel中绘制正态分布曲线，可以使用折线图或散点图。

具体步骤如下：
1.将随机变量X的取值范围输入到Excel的一个列中，例如，在A列中输入-3,-
2.9,-2.8,...,2.8,2.9,3，表示X的取值范围为-3到3，步长为0.1。

2.在另一个列中输入随机变量X对应的概率密度函数值，例如，在B列中输入=NORM.DIST(A1,1,1,FALSE)，并将此公式复制到下面的单元格中，直到填满整个列。

3.选中A列和B列中的所有数据，点击插入菜单中的折线图或散点图，即可绘制出正态分布曲线。

4.可以根据需要对图表进行格式调整，例如，调整坐标轴范围
和标签，添加标题和图例等。

绘制正态分布曲线是Excel中常见的数据可视化任务之一，掌握这一技能可以帮助我们更好地理解和分析数据。

excel 拟合正态分布
Excel是一款功能强大的电子表格软件，能够进行各种统计分析和数据处理。

其中，拟合正态分布是Excel中的一个重要功能。

正态分布是自然界中非常常见的一种分布形式，也称为高斯分布。

在Excel中，可以通过使用“数据分析”工具中的“拟合曲线”功能来拟合正态分布。

具体步骤如下：
1. 打开Excel，并打开需要进行拟合的数据表格。

2. 点击“数据”选项卡，在“分析”组中找到“数据分析”命令，点击。

3. 在弹出的“数据分析”对话框中，选择“回归”选项，并点
击“确定”。

4. 在“回归”对话框中，选择“拟合曲线”选项，并勾选“标
准误差”和“置信水平”选项。

5. 在“拟合曲线”下拉菜单中，选择“正态分布”。

6. 配置其他参数，如选择需要拟合的数据列、置信水平等。

7. 点击“确定”按钮，Excel会自动拟合正态分布，并输出相
关统计数据和参数。

通过拟合正态分布，我们可以更好地了解数据的分布规律，进一步进行数据分析和决策。

- 1 -。

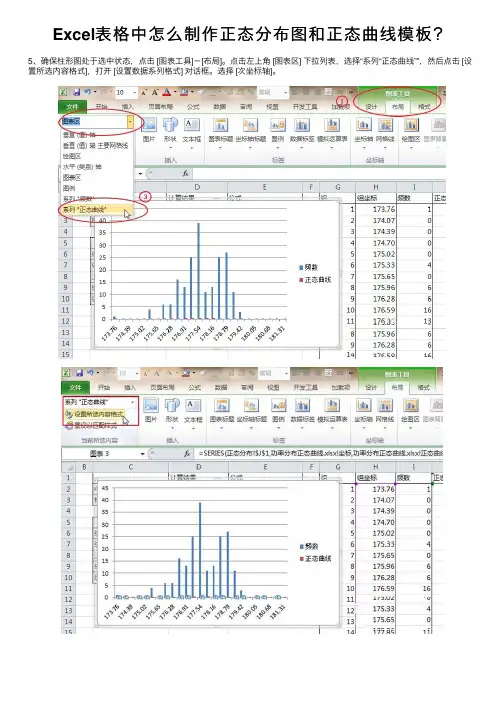
Excel表格中怎么制作正态分布图和正态曲线模板？5、确保柱形图处于选中状态，点击 [图表⼯具]－[布局]。

点击左上⾓ [图表区] 下拉列表，选择“系列“正态曲线””，然后点击 [设置所选内容格式]，打开 [设置数据系列格式] 对话框。

选择 [次坐标轴]。

6、 [图表⼯具] 选项组切换到 [设计] 选项卡。

点击 [更改图表类型]，打开 [更改图表类型] 对话框。

如图选择拆线图7、柱形图中选中正态曲线，然后在 [图表⼯具] 选项组切换到 [布局] 选项卡。

点击 [设置所选内容格式]，打开 [设置数据系列格式] 对话框。

切换到 [线型] ，选择 [平滑线]。

8、⾄此，图形已经画完。

如果只需要柱形分布图，不需要正态曲线，在柱形图中选中正态曲线，按键盘上的Delete键删除就⾏了。

有的专业作图软件中，柱形分布图中柱⼦是紧挨在⼀起的。

要这样设置的话请在柱形图中选中柱⼦，然后 [图表⼯具] 选项组切换到 [布局] 选项卡。

点击 [设置所选内容格式]，打开 [设置数据系列格式] 对话框。

分类间距设为0%。

切换到 [边框颜⾊] ，然后选择 [实线] ，颜⾊随便选⼀个，只要和柱⼦不是⼀个颜⾊就可以了。

这⾥选择了⿊⾊。

9、最后，试着修改下“组”和上下限与中⼼值距离的值，图表会⾃动更新。

在第3步中，我们计算了100组的值，所以，只要此处的组不超过100，均可得到正确的图表。

⼀般分组到100的情况极少，所以，第3步预留了100组的数据，以便在更改组时，总能等到正确的图表。

当然，如果你原意，计算1000组也⽆所谓了。

反正你已经学会⽅法了。

以后如果样本数据变更了，直接将A列数据换成新的样本数据，设置下需要的分组和上下限与中⼼值距离的值，正态分布图分分钟钟就出来啦。

⾄于美化嘛，只要更改相关设置就可以了，⽐如开篇那张，当然，你可以把图表美化的更加漂亮，尽情发挥想象⼒吧。

上⼀页12 3下⼀页阅读全⽂。

正态分布函数的语法是NORMDIST(x，mean，standard_dev，cumulative)cumulative为一逻辑值，如果为0则是密度函数，如果为1则是累积分布函数。

如果画正态分布图，则为0。

例如均值10%，标准值为20%的正态分布，先在A1中敲入一个变量，假定－50，选中A列，点编辑－填充－序列，选择列，等差序列，步长值10，终止值70。

然后在B1中敲入NORMDIST（A1，10，20，0），返回值为0.000222，选中B1，当鼠标在右下角变成黑十字时，下拉至B13，选中A1B13区域，点击工具栏上的图表向导－散点图，选中第一排第二个图，点下一步，默认设置，下一步，标题自己写，网格线中的勾去掉，图例中的勾去掉，点下一步，完成。

图就初步完成了。

下面是微调把鼠标在图的坐标轴上点右键，选坐标轴格式，在刻度中填入你想要的最小值，最大值，主要刻度单位（x轴上的数值间隔），y轴交叉于（y为0时，x多少）等等。

确定后，正态分布图就大功告成了。

PS：标准正态分布的语法为NORMSDIST(z)，正态分布（一）NORMDIST函数利用Excel计算正态分布，可以使用函数。

格式如下：变量，均值，标准差，累积，其中：变量：为分布要计算的值；均值：分布的均值；标准差：分布的标准差；累积：若1，则为分布函数；若0，则为概率密度函数。

当均值为0，标准差为1时，正态分布函数即为标准正态分布函数。

例3已知考试成绩服从正态分布，，，求考试成绩低于500分的概率。

解在Excel中单击任意单元格，输入公式：“ 500，600，100，1 ”，得到的结果为0.158655，即，表示成绩低于500分者占总人数的15.8655%。

例4假设参加某次考试的考生共有2000人，考试科目为5门，现已知考生总分的算术平均值为360，标准差为40分，试估计总分在400分以上的学生人数。

假设5门成绩总分近似服从正态分布。

解设表示学生成绩的总分，根据题意，，。

在学习工作中总会有一些用到直方图、正态分布曲线图的地方，下面手把手教大家在Excel2007中制作直方图和正态分布曲线图工具/原料•Excel(2007)•方法/步骤.1.数据录入.新建Excel文档，录入待分析数据（本例中将数据录入A列，则在后面引用中所有的数据记为A:A）；..2.计算“最大值”、“最小值”、“极差”、“分组数”、“分组组距”，公式如图：...3.分组.“分组”就是确定直方图的横轴坐标起止范围和每个小组的起止位置。

选一个比最小值小的一个恰当的值作为第一个组的起始坐标，然后依次加上“分组组距”，直到最后一个数据值比“最大值”大为止。

这时的实际分组数量可能与计算的“分组数”有一点正常的差别。

类似如下图。

...4.统计频率.“频率”就是去统计每个分组中所包含的数据的个数。

..最简单的方法就是直接在所有的数据中直接去统计，但当数据量很大的时候，这种方法不但费时，而且容易出错。

..一般来说有两种方法来统计每个小组的数据个数：1.采用“FREQUENCY”函数；2.采用“COUNT IF”让后再去相减。

..这里介绍的是“FREQUENCY”函数方法：.“Date_array”：是选取要统计的数据源，就是选择原始数据的范围；.“Bins_array”：是选取直方图分组的数据源，就是选择分组数据的范围；...5.生成“FREQUENCY”函数公式组，步骤如下：.1. 先选中将要统计直方图每个子组中数据数量的区域...6 .2. 再按“F2”健，进入到“编辑”状态...7.3. 再同时按住“Ctrl”和“Shift”两个键，再按“回车Enter”键，最后三键同时松开，大功告成！...8.制作直方图.选中统计好的直方图每个小组的分布个数的数据源（就是“频率”），用“柱形图”来完成直方图：.选中频率列下所有数据（G1:G21),插入→柱形图→二维柱形图..9.修整柱形图.选中柱形图中的“柱子”→右键→设置数据系列格式：.1、系列选项，分类间距设置为0%；.2、边框颜色：实线，白色（你喜欢的就好）3、关闭“设置数据系列格式”窗口...10 .直方图大功造成！..END.制作正态分布图.获取正态分布概念密度.正态分布概率密度正态分布函数“NORMDIST”获取。

excel有个数据分析工具，里面可以做直方图，但是正态分布图不能直接做。

若要两种图都显示，那么就需要用到函数了。

方法如下：
假若你的数据在A1:A10
1.统计数据个数；任意选个单元格，如B1，输入count(A1:A10)；
2.求最大值；如B2中输入：max(A1:A10)
3.求最小值；如B3中输入：min(A1:A10)
4.求平均值；如B4中输入：average(A1:A10)
5.求标准偏差：如B5中输入：stdev(A1:A10)
6.获得数据区间；用最大值减最小值；如B6中输入：B3-B2
7.获得直方图个数；个数的开放加1，如B7中输入：sqrt（B1）+1
8.获得直方图组距；用区间除以(直方图个数-1)，如B8中输入B7/(B7-1)
下面就开始作图了：
1.任选个空单元格：如C列第一个单元格C1，令C1等于最小值，即输入=B3
2.在C2中输入=C1+$B$8 (最小值逐渐累加，绝对引用)
3.选中C2，然后向下拉，直到数据大于最大值就可以了；比如你拉到C5了。

4.统计频数，如在D1中输入frequency（A1:A10，C1:C5）确定，然后将选中D1到D5，将光标定位到公式栏，同时按住ALT+Shift+Enter
5.统计正态分布的数据，E1中输入normdist（C1，$B$4,$B$5,0）回车；然后选中E1，下拉到E5
选择数据区域-二维堆积柱形图-确定完成，点击二维堆积柱形图的上数据图-右键-更改系列图标类型-选择折线图-图标空白处-右键-设置数据系列格式,看图吧：
-----
----
----
------
--。

在Excel 中，可以使用以下步骤生成正态分布曲线：1. 准备数据：准备一组数据，可以是任意数量的数据点，但最好不要太多，否则会使曲线变得过于平滑。

2. 计算均值和标准差：使用Excel 内置的公式计算数据的均值和标准差。

均值公式为=AVERAGE(data)，标准差公式为=STDEV.P(data)。

其中，data 是要计算标准差的数据列或数组的名称。

3. 绘制散点图：在Excel 中选择数据列或数组，右键单击并选择“插入”选项卡，然后选择“散点图”选项。

在弹出的菜单中，选择“散点图（散点图）”选项。

4. 添加误差线：在绘制的散点图上，选择要添加误差线的散点，然后右键单击并选择“添加数据标签”选项。

接下来，右键单击数据标签并选择“编辑数据标签”选项。

在弹出的菜单中，选择“数据标签包含”选项中的“位置”选项，并将“最小值”和“最大值”设置为数据的最小值和最大值。

5. 绘制正态分布曲线：在Excel 中选择散点图，右键单击并选择“添加趋势线”选项。

在弹出的菜单中，选择“线性趋势线”选项，然后选择“显示方程式”和“显示R²”选项。

接下来，单击“确定”按钮并选择要添加趋势线的散点，以确保趋势线正确地连接了散点。

6. 添加正态分布曲线：在绘制的散点图上，选择要添加正态分布曲线的散点，右键单击并选择“添加图表元素”选项。

在弹出的菜单中，选择“数据标签”选项，并选择“数据标签包含”选项中的“位置”选项，并将“最小值”和“最大值”设置为数据的最小值和最大值。

7. 调整正态分布曲线：使用Excel 的图表工具调整正态分布曲线的样式、颜色和标签等属性，以使其更符合实际情况。

以上是在Excel 中生成正态分布曲线的基本步骤，需要注意的是，生成的正态分布曲线可能会因为数据的不同而有所不同，需要根据实际情况进行调整。

制作直方图
1、数据录入
新建Excel文档，录入待分析数据（本例中将数据录入A列，则在后面引用中所有的数据记为A:A）；2
2、计算最大值、最小值、极差、分组数、分组组距
其中：极差=最大值-最小值，分组数=数据的平方根向上取整，分组组距=极差/分组数
3、分组
分组就是确定直方图的横轴坐标起止范围和每个小组的起止位置。

选一个比最小值小的一个恰当的值作为第一个组的起始坐标，然后依次加上“分组组距”，直到最后一个数据值比“最大值”大为止。

这时的实际分组数量可能与计算的“分组数”有一点正常的差别。

4、统计频率
5、制作直方图
选中统计好的直方图每个小组的分布个数的数据源（就是“频率”），用“柱形图”来完成直方图：选中频率列下所有数据（G1:G21),插入→柱形。

excel画正态分布曲线图Excel是微软公司出品的办公软件，使用非常广泛。

它不仅可以用来处理各种表格，还可以制作精美的图表。

本文将介绍如何使用Excel来画正态分布曲线图。

首先，我们需要准备一份数据表，该表应包含来自观测值的观测数据。

在Excel中，将数据表格式设置为“简单表格”，然后把数据复制到此表格中。

接下来，在新工作表中插入正态分布曲线图。

打开图表编辑器，点击“图表类型”，然后选择“曲线图”，点击“确定”。

接着，在“数据”标签中，选择“添加数据”，并将Excel中的数据表中的数据复制到此框中。

点击“确定”，曲线图就生成了。

接下来，我们就可以对正态分布曲线图进行美化了。

先把X轴的标题改成“观测值”，Y轴标题改成“概率”，然后把曲线的粗细调整一下，把颜色改成你喜欢的颜色，最后可以把图表的标题改成“正态分布图”，这样就可以得到一幅精美的正态分布图了。

正态分布图有很多用途，它可以帮助用户更好地分析和理解数据。

例如，我们可以使用正态分布图查看一组观测数据的分布规律。

我们可以看到，这些观测值有多少在平均值附近，有多少偏离平均值。

另外，正态分布图还可以用来评估观测数据是否符合正态分布，以及观测数据的变异情况。

最后，我们可以介绍一下使用Excel画正态分布曲线图的优势。

Excel是一款只需要很少的操作就可以搞定的软件，使用它画正态分布曲线图相当容易，而且能得到较高质量的曲线图，并且可以在图表中添加更多的新元素，比如说添加坐标轴的网格线、标题等等，让曲线图变得更为美观。

以上就是本文关于“Excel画正态分布曲线图”的内容，希望本文能够帮助读者学会如何使用Excel来制作正态分布曲线图，深入了解正态分布图的特点以及它的用途，也希望读者在制作这种图表时能够节省时间，得到更好的效果。

excel生成正态曲线
在Excel中生成正态曲线可以通过以下步骤实现。

首先，打开Excel并创建一个新的工作表。

然后按照以下步骤操作：
1. 在一个列中输入一系列代表正态分布的X值。

例如，可以输
入-3、-2.5、-2、-1.5、-1、-0.5、0、0.5、1、1.5、2、2.5、3
等数值。

2. 在另一列中，使用正态分布函数NORM.DIST来计算对应X值
的Y值。

该函数的语法为
=NORM.DIST(x,mean,standard_dev,cumulative)，其中x是要计算
的值，mean是正态分布的均值，standard_dev是正态分布的标准差，cumulative是一个逻辑值，用于指定计算累积分布函数还是概率密
度函数。

例如，可以使用=NORM.DIST(A2,0,1,FALSE)来计算X值为
A2的概率密度函数值。

3. 将上述公式拖动或填充到下面的单元格，以计算所有X值对
应的Y值。

4. 选择X和Y值的数据范围，然后插入散点图。

在Excel中，
选择“插入”选项卡，然后选择“散点图”图标。

选择适当的散点图类型，确保X轴是你输入的X值，Y轴是计算得到的Y值。

5. 在生成的散点图上，右键单击数据点，然后选择“添加趋势线”。

在弹出的对话框中，选择“正态分布”作为趋势线类型。

通过上述步骤，你就可以在Excel中生成一个代表正态分布的曲线图表。

这样可以直观地展示正态分布的特征，对于数据分析和可视化非常有帮助。

希望这些步骤能帮助到你。