函数的概念和图象课件1(苏教版必修1)
- 格式:ppt
- 大小:256.05 KB
- 文档页数:4

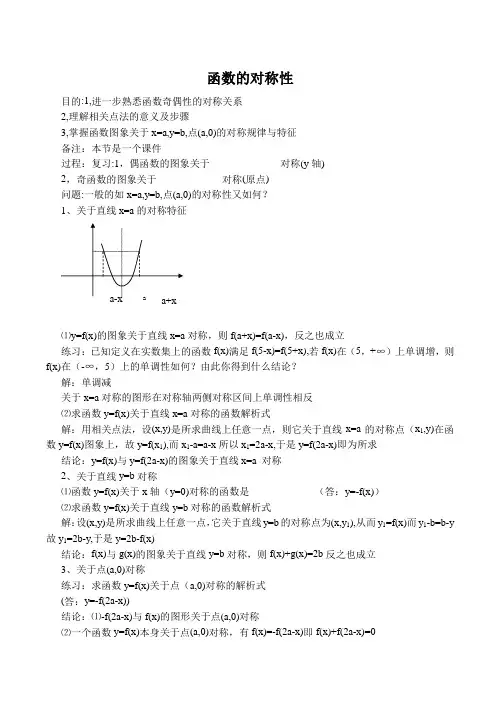
函数的对称性目的:1,进一步熟悉函数奇偶性的对称关系2,理解相关点法的意义及步骤3,掌握函数图象关于x=a,y=b,点(a,0)的对称规律与特征备注:本节是一个课件过程:复习:1,偶函数的图象关于______________对称(y轴)2,奇函数的图象关于_____________对称(原点)问题:一般的如x=a,y=b,点(a,0)的对称性又如何?1、关于直线x=a的对称特征⑴y=f(x)的图象关于直线x=a对称,则f(a+x)=f(a-x),反之也成立练习:已知定义在实数集上的函数f(x)满足f(5-x)=f(5+x),若f(x)在(5,+∞)上单调增,则f(x)在(-∞,5)上的单调性如何?由此你得到什么结论?解:单调减关于x=a对称的图形在对称轴两侧对称区间上单调性相反⑵求函数y=f(x)关于直线x=a对称的函数解析式解:用相关点法,设(x,y)是所求曲线上任意一点,则它关于直线x=a的对称点(x1,y)在函数y=f(x)图象上,故y=f(x1),而x1-a=a-x所以x1=2a-x,于是y=f(2a-x)即为所求结论:y=f(x)与y=f(2a-x)的图象关于直线x=a 对称2、关于直线y=b对称⑴函数y=f(x)关于x轴(y=0)对称的函数是_____________(答:y=-f(x))⑵求函数y=f(x)关于直线y=b对称的函数解析式解:设(x,y)是所求曲线上任意一点,它关于直线y=b的对称点为(x,y1),从而y1=f(x)而y1-b=b-y 故y1=2b-y,于是y=2b-f(x)结论:f(x)与g(x)的图象关于直线y=b对称,则f(x)+g(x)=2b反之也成立3、关于点(a,0)对称练习:求函数y=f(x)关于点(a,0)对称的解析式(答:y=-f(2a-x))结论:⑴-f(2a-x)与f(x)的图形关于点(a,0)对称⑵一个函数y=f(x)本身关于点(a,0)对称,有f(x)=-f(2a-x)即f(x)+f(2a-x)=0总结:本节主要说明了以下几个对称问题:⑴y=f(x)的图象关于直线x=a对称,则f(a+x)=f(a-x),反之也成立;关于x=a对称的图形在对称轴两侧对称区间上单调性相反;y=f(x)与y=f(2a-x)的图象关于直线x=a 对称⑵f(x)与g(x)的图象关于直线y=b对称,则f(x)+g(x)=2b反之也成立⑶-f(2a-x)与f(x)的图形关于点(a,0)对称;一个函数y=f(x)本身关于点(a,0)对称,有f(x)=-f(2a-x)即f(x)+f(2a-x)=0课上练习1,已知函数y=|x+1|-|x-2|画出其图象,说明它关于哪个点对称(不必证明),并指出函数的最值。