第2章 平面连杆机构
- 格式:doc
- 大小:409.00 KB
- 文档页数:11




第二章平面连杆机构及其设计【基本要求】1.了解平面四杆机构的基本型式,掌握其演化方法。
2.掌握平面四杆机构的工作特性。
3.了解连杆机构传动的特点及其功能。
4.掌握平面连杆机构运动分析的方法,学会将复杂的平面连杆机构的运动分析问题转化为可用计算机解决的问题。
5.了解平面连杆机构设计的基本问题,熟练掌握根据具体设计条件及实际需要,选择合适的机构型式和合理的设计方法,解决具体设计问题。
【重点难点】本章内容包括平面连杆机构和空间连杆机构两部分,其中平面连杆机构是本章的重点。
通过本章的学习,最终要求达到:根据实际需求,确定满足此需求的连杆机构类型,选择合适的设计方法设计出此连杆机构。
设计完成后需对所设计的连杆机构进行运动学和动力学分析,校验此机构是否实用,是否满足实际要求。
【学习内容】平面连杆机构是常用的低副机构,其中以由四个构件组成的四杆机构应用最广泛,而且是组成多杆机构的基础。
因此本章着重讨论四杆机构的基本类型、性质及常用设计方法。
2.1 铰链四杆机构的类型及应用2.2 铰链四杆机构的曲柄存在条件2.3 铰链四杆机构的演化2.4 平面四杆机构的基本特性2.5 平面四杆机构的设计平面连杆机构若各运动构件均在相互平行的平面内运动,则称为平面连杆机构。
空间连杆机构若各运动构件不都在相互平行的平面内运动,则称为空间连杆机构。
平面连杆机构较空间连杆机构应用更为广泛,故着重介绍平面连杆机构。
在平面连杆机构中,结构最简单的且应用最广泛的是由4个构件所组成的平面四杆机构,其它多杆机构可看成在此基础上依次增加杆组而组成。
●下面介绍平面四杆机构的基本型式及其演化。
铰链四杆机构所有运动副均为转动副的四杆机构称为铰链四杆机构。
它是平面四杆机构的基本型式。
2.1 铰链四杆机构的类型及应用2.1.1铰链四杆机构的类型由转动副联接四个构件而形成的机构,称为铰链四杆机构,奴图所示。
图中固定不动的构件AD是机架;与机架相连的构件AB、CD称为连架杆;不与机架直接相连的构件BC称为连杆。
第2章平面连杆机构2.1平面连杆机构的特点和应用连杆机构是由若干刚性构件用低副连接组成的机构,又称为低副机构。
在连杆机构中,若各运动构件均在相互平行的平面内运动,称为平面连杆机构;若各运动构件不都在相互平行的平面内运动,则称为空间连杆机构。
平面连杆机构被广泛应用在各类机械中,之所以广泛应用,是因为它有较显著的优点:(1)平面连杆机构中的运动副都是低副,其构件间为面接触,传动时压强较小,便于润滑,因而磨损较轻,可承受较大载荷。
(2)平面连杆机构中的运动副中的构件几何形状简单(圆柱面或平面),易于加工。
且构件间的接触是靠本身的几何约束来保持的,所以构件工作可靠。
(3)平面连杆机构中的连杆曲线丰富,改变各构件的相对长度,便可使从动件满足不同运动规律的要求。
另外可实现远距离传动。
平面连杆机构也存在一定的局限性,其主要缺点如下:(1)根据从动件所需要的运动规律或轨迹设计连杆机构比较复杂,精度不高。
(2)运动时产生的惯性力难以平衡,不适用于高速的场合。
(3)机构中具有较多的构件和运动副,则运动副的间隙和各构件的尺寸误差使机构存在累积误差,影响机构的运动精度,机械效率降低。
所以不能用于高速精密的场合。
平面连杆机构具有上述特点,所以广泛应用于机床、动力机械、工程机械等各种机械和仪表中。
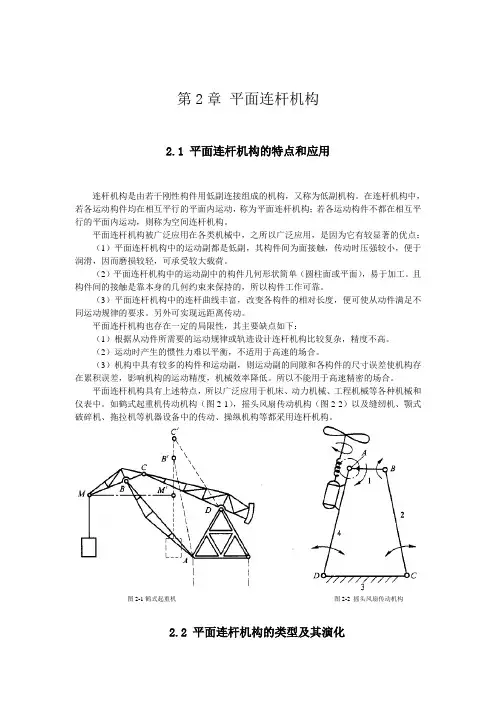
如鹤式起重机传动机构(图2-1),摇头风扇传动机构(图2-2)以及缝纫机、颚式破碎机、拖拉机等机器设备中的传动、操纵机构等都采用连杆机构。
图2-1鹤式起重机图2-2 摇头风扇传动机构2.2平面连杆机构的类型及其演化2.2.1 平面四杆机构的基本形式全部用转动副组成的平面四杆机构称为铰链四杆机构,如图2-3所示。
机构的固定件4称为机架;与机架相联接的杆1和杆3称为连架杆;不与机架直接联接的杆2称为连杆。
能作整周转动的连架杆,称为曲柄。
仅能在某一角度摆动的连架杆,称为摇杆。
按照连架杆的运动形式,将铰链四杆机构分为三种基本型式:曲柄摇杆机构、双曲柄机构和双摇杆机构。



第2章平面连杆机构平面连杆机构是由若干构件通过低副联接而成的平面机构,也称平面低副机构。
平面连杆机构广泛应用于各种机械和仪表中,其主要优点是:(1)由于运动副是低副,面接触,传力时压强小,磨损较轻,承载能力较高;(2)构件的形状简单,易于加工,构件之间的接触由构件本身的几何约束来保持,故工作可靠;(3)可实现多种运动形式及其转换,满足多种运动规律的要求;(4)利用平面连杆机构中的连杆可满足多种运动轨迹的要求。
主要缺点有:(1)由于低副中存在间隙,机构不可避免地存在着运动误差,精度不高,(2)主动构件匀速运动时,从动件通常为变速运动,故存在惯性力,不适用于高速场合。
平面机构常以其组成的构件(杆)数来命名,如由四个构件通过低副联接而成的机构称为四杆机构,而五杆或五杆以上的平面连杆机构称为多杆机构。
四个机构是平面连杆机构中最常见的形式,也是多杆机构的基础。
1.1 四杆机构的基本形式及其演化1.1.1 四杆机构的基本形式构件间的运动副均为转动副联接的四杆机构,是四杆机构的基本形式,称为铰链四杆机构,如图1-1所示。
由三个活动构件和一个固定构件(即机架)组成。
其中,AD杆是机架,与机架相对的杆(BC杆)称为连杆,与机架相联的构件(AB杆和CD杆)称为连架杆,能绕机架作360°回转的连架杆称为曲柄,只能在小图1-1于360°范围内摆动的连架杆称为摇杆。
根据两连架杆的运动形式的不同,铰链四杆机构可分为三种基本形式并以其连架杆的名称组合来命名。
(1)曲柄摇杆机构两连架杆中一个为曲柄另一个为摇杆的四杆机构,称为曲柄摇杆机构。
曲柄摇杆机构中,当以曲柄为原动件时,可将曲柄的匀速转动变为从动件的摆动。
如图1-2所示的雷达天线机构,当原动件曲柄1转动时,通过连杆2,使与摇杆3固结的抛物面天线作一定角度的摆动,以调整天线的俯仰角度。
图1-3为汽车前窗的刮雨器,当主动曲柄AB回转时,从动摇杆作往复摆动,利用摇杆的延长部分实现刮雨动作。



第2章平面连杆机构教案(精选5篇)第一篇:第2章平面连杆机构教案第2章平面连杆机构平面连杆机构——由若干个构件通过平面低副(转动副和移动副)联接而构成的平面机构,也叫平面低副机构平面连杆机构具有承载能力大、结构简单、制造方便等优点,用它可以实现多种运动规律和运动轨迹,但只能近似地实现所要求的运动。
最简单的平面连杆机构由四个构件组成,简称平面四杆机构。
是组成多杆机构的基础只介绍四杆机构§2-1 平面四杆机构的基本类型及其应用一,铰链四杆机构铰链四杆机构——全部由回转副组成的平面四杆机构,它是平面四杆机构最基本的形态。
如图2-1a所示,铰链四杆机构由机架4、连架杆(与机架相连的 1、3两杆)和连杆(与机架不相联的中间杆2)组成。
如图所示曲柄——能绕机架上的转动副作整周回转的连架杆。
摇杆——只能在某一角度范围(小于360°)内摆动的连架杆。
铰链四杆机构按照连架杆是曲柄还是摇杆分为曲柄摇杆机构、双曲柄机构、双摇杆机构三种基本型式。
1、曲柄摇杆机构曲柄摇杆机构——两连架杆中一个是曲柄,一个是摇杆的铰链四杆机构。
当曲柄为原动件时,可将曲柄的连续转动,转变为摇杆的往复摆动。
应用:雷达调整机构2、双曲柄机构两连架杆均为曲柄的铰链四杆机构称为双曲柄机构。
当原动曲柄连续转动时,从动曲柄也作连续转动如图所示在双曲柄机构中,若其相对两杆相互平行如右图所示,则成为或平行四边形机构(平行双曲柄机构)。
如图所示当平行四边形机构的四个铰链中心处于同一条直线上时,将出现运动不确定状态,一般采用相同机构错位排列的方法,来消除这种运动不确定状态。
如图所示应用:在机车车轮联动机构中,则是利用第三个平行曲柄来消除平行四边形机构在这种死点位置的运动不确定性。
3、双摇杆机构两连架杆均为摇杆的铰链四杆机构称为双摇杆机构应用:飞机起落架通过用移动副取代转动副、变更杆件长度、变更机架和扩大转动副等途径,可以得到铰链四杆机构的其他演化型式二,含一个移动副的四杆机构 1,曲柄滑块机构通过将摇杆改变为滑块,摇杆长度增至无穷大,可得到曲柄滑块机构,如图所示对心曲柄滑块机构与偏置曲柄滑块机构曲柄滑块机构应用于活塞式内燃机2、导杆机构在图所示曲柄滑块机构中,若改取杆1为固定构件,即得导杆机构。
第2章平面连杆机构
题2-1 试根据图2.14 中标注尺寸判断下列铰链四杆机构是曲柄摇杆机构、双曲柄机构,还是双摇杆机构。
a )
b )
c )
d )
图2.14
题2-2 试运用铰链四杆机构有整转副的结论,推导图2.15 所示偏置导杆机构成为转动导杆机构的条件(提示:转动导杆机构可视为双曲柄机构)。
图2.15
题2-3 画出图2.16 所示各机构的传动角和压力角。
图中标注箭头的构件为原动件。
图2.16
题2-4 已知某曲柄摇杆机构的曲柄匀速转动,极位夹角为,摇杆工作行程须时7s 。
试问:
(1 )摇杆空回行程需几秒?(2 )曲柄每分钟转速是多少?
题2-5 设计一脚踏轧棉机的曲柄摇杆机构,要求踏板在水平位置上下各摆,且
,。
(1 )试用图解法求曲柄和连杆的长度;(2 )用公式(2-3 )和(2-3 )′ 计算此机构的最小传动角。
图2.17 题2-5 解图
题2-6 设计一曲柄摇杆机构。
已知摇杆长度,摆角,摇杆的行程速度变化系数。
(1 )用图解法确定其余三杆的尺寸;( 2 )用公式( 2 — 3 )和(2-3 )′确定机构最小传动角(若,则应另选铰链A 的位置,重新设计)。
题2-7 设计一曲柄滑块机构。
已知滑块的行程,偏距,行程速度变化系数。
求曲柄和连杆的长度。
图2.19
题2-8 设计一导杆机构。
已知机架长度,行程速度变化系数,求曲柄长度。
图2.20
题2-9 设计一曲柄摇杆机构。
已知摇杆长度,摆角,摇杆的行程速度变化系数,且要求摇杆的一个极限位置与机架间的夹角,试用图解法确定其余三杆的长度。
图2.21
题2-10 设计一铰链四杆机构作为加热炉门的启闭机构。
已知炉门上的两活动铰链中心距为,炉门打开后成水平位置时,要求炉门温度较低的一面朝上(如虚线所示),设固定铰链
安装在轴线上,其相关尺寸如图所示,求此铰链四杆机构其余三杆的长度。
图2.22
题2-11 设计一铰链四杆机构。
已知其两连架杆的四组对应位置间的夹角为,
、,,试用实验法求各杆长度,并绘出机构简图。
题2-12 已知某操纵装置采用铰链四杆机构。
要求两连架杆的对应位置如2.24 所图所示,,;,;,,机架长度
,
试用解析法求其余三杆长度。
图2.24
题2-13 图2.25 所示机构为椭圆仪中的双滑块机构,试证明当机构运动时,构件2 的直线上任一点(除、及的中点外)所画的轨迹为一椭圆。
图2.25
答案
题2-1答: a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题2-2解: 要想成为转动导杆机构,则要求与均为周转副。
(1 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15 中位置
和。
在中,直角边小于斜边,故有:(极限情况取等号);
在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
(2 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15 中位置
和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);
在位置时,因为导杆是无限长的,故没有过多条件限制。
(3 )综合(1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:
题2-3 见图 2.16 。
图2.16
题2-4解: (1 )由公式,并带入已知数据列方程有:
因此空回行程所需时间;
(2 )因为曲柄空回行程用时,
转过的角度为,
因此其转速为:转/ 分钟
题2-5
解: (1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此
时
曲柄与连杆处于两次共线位置。
取适当比例图尺,作出两次极限位置和(见图
2.17 )。
由图量得:,。
解得:
由已知和上步求解可知:
,,,
(2 )因最小传动角位于曲柄与机架两次共线位置,因此取和代入公式(2-3 )计算可得:
或:
代入公式(2-3 )′,可知
题2-6解:因为本题属于设计题,只要步骤正确,答案不唯一。
这里给出基本的作图步骤,不
给出具体数值答案。
作图步骤如下(见图2.18 ):
(1 )求,;并确定比例尺。
(2 )作,。
(即摇杆的两极限位置)
(3 )以为底作直角三角形,,。
(4 )作的外接圆,在圆上取点即可。
在图上量取,和机架长度。
则曲柄长度,摇杆长度。
在得到具体各杆数据之后,代入公式(2 — 3 )和(2-3 )′求最小传动角,能满足即可。
图2.18
题2-7
图2.19
解: 作图步骤如下(见图2.19 ):
(1 )求,;并确定比例尺。
(2 )作,顶角,。
(3 )作的外接圆,则圆周上任一点都可能成为曲柄中心。
(4 )作一水平线,于相距,交圆周于点。
(5 )由图量得,。
解得:
曲柄长度:
连杆长度:
题2-8
解: 见图2.20 ,作图步骤如下:
(1 )。
(2 )取,选定,作和,。
(3 )定另一机架位置:角平
分线,。
(4 ),。
杆即是曲柄,由图量得曲柄长度:
题2-9解:见图2.21 ,作图步骤如下:
(1 )求,,由此可知该机构没有急回特性。
(2 )选定比例尺,作,。
(即摇杆的两极限位置)(3 )做,与交于点。
(4 )在图上量取,和机架长度。
曲柄长度:
连杆长度:
题2-10解: 见图2.22 。
这是已知两个活动铰链两对位置设计四杆机构,可以用圆心法。
连接,,作图2.22 的中垂线与交于点。
然后连接,,作的中垂线
与交于点。
图中画出了一个位置。
从图中量取各杆的长度,得到:
,
,
题2-11解: (1 )以为中心,设连架杆长度为,根据作出,,。
(2 )取连杆长度,以,,为圆心,作弧。
(3 )另作以点为中心,、,的另一连架杆的几个位置,并作出不同
半径的许多同心圆弧。
(4 )进行试凑,最后得到结果如下:,,,。
机构运动简图如图2.23 。
题2-12解: 将已知条件代入公式(2-10 )可得到方程组:
联立求解得到:
,,。
将该解代入公式(2-8 )求解得到:
,,,。
又因为实际,因此每个杆件应放大的比例尺为:
,故每个杆件的实际长度是:
,,
,。
题2-13证明: 见图2.25 。
在上任取一点,下面求证点的运动轨迹为一椭圆。
见图可知点将分为两部分,其中,。
又由图可知,,二式平方相加得
可见点的运动轨迹为一椭圆。