2018届绵阳二诊试卷评讲(南山实验周德伟)

绝密*启用前(考试时间：2018年1月11日下午3：00—5：30)绵阳市高中2018级第二次诊断性考试文科综合能力测试本试卷分为试题卷和答题卷两部分，其中试题卷由第1卷’(选择题)和第Ⅱ卷(非选择题)组成，共10页；答题卷共4页。

满分300分。

考试结束后将答题卡和答题卷一并交回。

第1卷(选择题，共140分)注意事项：1．答第1卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案，不能答在试题卷上。

3．第1卷1—11小题为地理；12～23小题为历史；24～35小题为思想政治。

一、本卷共35小题，每小题4分，共计140分。

在每小题列出的四个选项中，只有一项是最符合题目要求的。

读下图判断1—4题：1．一架飞机在某理想状态下进行航空作业，从B地(400S)依次向北，向东，向南，向西各航行2500Km，然后降落于Q点，Q点的位置在A．恰好与B点重合B．位于B点正西方C.位于B点正东方D．位于B点东南方2．图中A、B、C、D四点中，年降水量最少的是A．A B．B C．C D．D3．有关甲、乙、丙三个阴影区域的叙述，正确的是A．甲地日出时，乙地可能是日落B．乙的比例尺大于甲，但小于丙C、甲地到丙地走最近路线不会通过乙地D．甲、乙、丙的面积相等4．乙和丙阴影区域所在地的两个主要国家，正确的说法是①都是人口超过一亿的大国②都有回归线经过③乙国是发展中国家，丙国是发达国家④乙国的粮食作物主要是水稻，丙国是天然橡胶的最大产国A．③④B．①② C.①④D．②③读下图判断5—7题：5．根据图上信息，判断该地区位于A．东北平原B．云贵高原 C.塔里木盆地D．青藏高原6．该地的人口密度小，其影响的主要因素是A．原生环境B．次生环境 C.社会环境D．人口迁移7．该地最适宜开展的经济活动是A．旅游B．航运C．牧业D．种植业读内蒙古商都县某地土地荒漠化的变化状况示意图，判断8—9题：8．图中所示的这种变化状况主要取决于A、地形因素B、气候因素C、降水状况D、人类活动9．该地区的自然景观特征正确的描述是A、深居内陆、受海洋影响小，降水量少B、日照时间长，积温高C、人类活动的历史悠久，人口密度大D、全年气温低、光照时数少下图为世界地图上的一段经线；M以北为陆地，N以南为陆地，MN之间为海洋，读图判断10一11题：10．下列国家中，位于MN所在海洋沿岸的是A、几内亚利比里亚B．印度巴基斯坦C、土耳其法国D．瑞典芬兰11．下列关于N所在国家的叙述，正确的是A．地跨亚洲和欧洲B．著名河流——密西西比河B．草场辽阔，畜牧业发达D．光照充足，适合长绒棉生长走向海洋，是一个国家发展、强大和开放的重要标志。

四川省绵阳市2018届高三第二次诊断考试理综物理试题一、选择题:本题共8小题,每小题6分。

在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19-21题有多项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分1. 如图所示,闭合开关S,将滑动变阻器R的滑片向右滑动的过程中A. 电流表A1的示数变小B. 电流表A2的示数变小C. 电压表V的示数变小D. 电阻R1的电功率变大【答案】A【解析】A、D、滑动变阻器左边部分的电阻并联接入电路,滑片向右滑动,并联的电阻增大,总电阻增大,由可知干路电流变小,则A1表的示数变小,根据可得电阻R1的电功率变大，则A正确、D正确.C、由可知并联部分的电压增大,即电压表的示数变大,C错误.B、由,因R2阻值不变则电流表A2的示数变大,则B错误。

故选A。

【点睛】要解答本题需要用到的知识有滑动变阻器的使用，电阻的串联和并联，串联电路的电压规律，欧姆定律及其应用，电功率的计算。

本题中的电路图是一个混联电路，分析时我们可以先局部后整体，解答本题的思路：先分析电阻变化情况-再分析电流变化情况-接着分析电压变化情况-最后得出电功率变化情况。

解答本题用到的核心知识是：欧姆定律。

另：不论电阻是串联还是并联，只要两个电阻中有一个电阻变大（或变小），则总电阻也会变大（或变小）。

2. 在水平地面上，两个具有相同初动量而质量不同的物体在大小相等的阻力作用下最后停下来。

则质量大的物体( )A. 滑行的距离小B. 滑行的时间长C. 滑行过程中的加速度大D. 滑行过程中的动量变化快【答案】A【解析】A、根据P=mv，可知，则可知，初动量相同，质量大的物体速度小；根据动能定理可知：，则可知质量大的物体滑行的距离小；故A正确；B、根据动量定理可知，-ft=0-P，因动量相同，故滑行时间相同，故B错误；C、因阻力相同，由牛顿第二定律可知，质量大的加速度小，故C错误；D、因两物体均停止，所以滑行过程中动量变化相同，因滑行时间相同，故动量变化相同，故D错误。

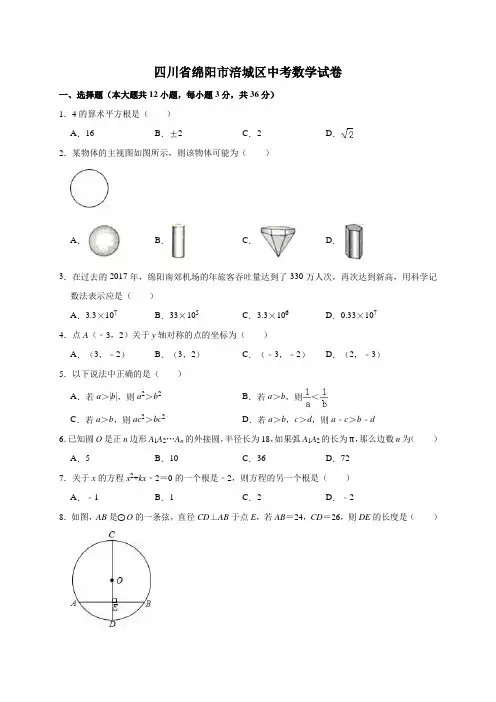
四川省绵阳市涪城区中考数学试卷一、选择题（本大题共12小题，每小题3分，共36分）1．4的算术平方根是（）A．16B．±2C．2D．2．某物体的主视图如图所示，则该物体可能为（）A．B．C．D．3．在过去的2017年，绵阳南郊机场的年旅客吞吐量达到了330万人次，再次达到新高，用科学记数法表示应是（）A．3.3×107B．33×105C．3.3×106D．0.33×1074．点A（﹣3，2）关于y轴对称的点的坐标为（）A．（3，﹣2）B．（3，2）C．（﹣3，﹣2）D．（2，﹣3）5．以下说法中正确的是（）A．若a＞|b|，则a2＞b2B．若a＞b，则＜C．若a＞b，则ac2＞bc2D．若a＞b，c＞d，则a﹣c＞b﹣d6．已知圆O是正n边形A1A2…A n的外接圆，半径长为18，如果弧A1A2的长为π，那么边数n为（）A．5B．10C．36D．727．关于x的方程x2+kx﹣2＝0的一个根是﹣2，则方程的另一个根是（）A．﹣1B．1C．2D．﹣28．如图，AB是⊙O的一条弦，直径CD⊥AB于点E，若AB＝24，CD＝26，则DE的长度是（）A．5B．6C．7D．89．如图，在小山的东侧A点有一个热气球，由于受风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A，B两点间的距离为（）米．A．750B．375C．375D．75010．如图是二次函数y＝ax2+bx+c图象的一部分，其对称轴为x＝﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b＝0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．①②④D．②③④11．如图，在平行四边形ABCD中，BC＝4，现将平行四边形ABCD绕点A旋转到平行四边形AEFG 的位置，其中点B，C，D分别落在点E，F，G处，且点B，E，D，F在同一直线上，如果点E 恰好是对角线BD的中点，那么AB的长度是（）A．4B．3C．2D．12．如果，一圆桌周围有20个箱子，依顺时针方向编号1～20，小明从1号箱子沿着圆桌依顺时针方向前进，每经过一个箱子就丢入一颗球，所有小球共有红、黄、绿3种颜色，1号箱子红色，2号箱子黄色，3号箱子绿色，4号红色，5号黄色，6号绿色……，颜色依次循环，当他围绕圆桌刚好丢完2018圈时，则第10号箱子有（）个黄球．A．671B．672C．673D．674二、填空题（本大题共6小题，每小题3分，共18分）13．因式分解：x2﹣9x+18＝．14．如图，直线l1，l2，l3交于一点，直线l4∥l1，若∠1＝124°，∠2＝88°，则∠3的度数为．15．一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机摸出两个小球，摸出两个颜色相同的小球的概率为．16．如图，点A的坐标为（3，），点B的坐标为（6，0），将△AOB绕点B按顺时针方向旋转一定的角度后得到△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为．17．如图，在菱形ABCD中，已知∠ABC＝60°，AB＝6，E为AD中点，BE与AC交于点O，F为EC上点，且OF∥BC，连接BF，BF与AC交于点M，则OM的长度是．18．如图，AB为⊙P直径，点O是⊙P上一点，以O为圆心，OA为半径的⊙O与AB交于点C，与OB交于点D，连接OC，AD，若OA＝5，△OAC的面积为12，则△ACD的面积是．三、解答题（本大题共7小题，共计86分）19．（16分）（1）计算：﹣2﹣1﹣（﹣π）0﹣4sin45°（2）先化简，再求值：（﹣1）÷，其中x＝320．（11分）共享单车近日成为市民新宠，越来越多的居民选择共享单车作为出行的交通工具，某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况，随机抽取了该小区部分使用共享单车的居民进行调查（问卷调查表如图所示），并用调查结果绘制了图①、图②两幅每周使用共享单车时间的人数统计图（均不完整），请根据统计图解答以下问题：（1）本次接受问卷调查的共有人；在扇形统计图中“D”选项所占的百分比为；（2）扇形统计图中，“B”选项所对应扇形圆心角为度；（3）请补全条形统计图；（4）若该小区共有1200名居民，请你估计该小区使用共享单车的时间在“A”选项的有多少人？21．（11分）请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个长方体形状的包装盒，E，F在AB上，是被切去的一个等腰直角三角形斜边的两个端点，设AE＝FB＝x（cm）．（1）若要求改包装盒的高是20cm（以图中所示位置为参照），则x的值应是多少？（2）某广告商要求包装盒的侧面积S（cm2）最大，试问x应取何值？22．（11分）在平面直角坐标系xOy中，反比例函数y1＝的图象与一次函数y2＝ax+b的图象交于点A（1，3）和B（﹣3，m）．（1）求反比例函数y1＝和一次函数y2＝ax+b的解析式；（2）点C是坐标平面内一点，且BC∥x轴，当∠BAC＝90°时，求点C坐标．23．（11分）如图，AB是⊙O直径，点C是⊙O上一点，D为的中点，AD与BC交于点M．（1）证明：△ACD∽△CMD；（2）若AC＝3，tan∠CBD＝，求△BCD的面积．24．（12分）已知抛物线y＝x2﹣ax与x轴交于O，A两点，点B（﹣1，3）在抛物线上，点C（0，m）（m＞3），延长BC与抛物线交于点E，过E作ED⊥x轴于点D，线段CD与抛物线交于点F，连接AB．（1）求抛物线解析式；（2）若四边形ABCD的面积为25，请求出点C坐标；（3）当m为何值时，四边形ABCF是平行四边形．25．（14分）如图，在平面直角坐标系xOy中，A（﹣8，0），B（﹣5，4），BC∥x轴，且与y轴交于点C，点D与点A关于y轴对称，连接CD．（1）若令∠CDA＝α，证明：∠BAD＝2α；（2）如图1，点M为线段BC上动点（不与端点重合），N为射线CD上点，且∠AMN＝∠ABC，若令BM＝m，请求出点N坐标（用含m的代数式表示）；（3）如图2，点E在线段AB上，其横坐标为﹣6，作EF∥x轴，且与CD交于点F，在EF延长线上有动点P，射线FD上有点Q，且∠APQ＝∠ABC，若＝t，求的值（用含t的代数式表示）．2018年四川省绵阳市涪城区中考数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题3分，共36分）1．【分析】算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵2的平方为4，∴4的算术平方根为2．故选：C．【点评】此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．2．【分析】根据主视图利用排除法确定正确的选项即可．【解答】解：A、球的主视图为圆，符合题意；B、圆柱的主视图为矩形，不符合题意；C、六棱柱与六棱锥的组合体的主视图为矩形和三角形的结合图，不符合题意；D、五棱柱的主视图为矩形，不符合题意，故选：A．【点评】本题考查了由三视图判断几何体的知识，解题的关键是能够了解各个几何体的主视图，难度不大．3．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：330万用科学记数法表示应是3.3×106，故选：C．【点评】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．4．【分析】关于y轴对称的点，纵坐标相同，横坐标互为相反数，可得答案．【解答】解：A（﹣3，2）关于y轴对称的点的坐标为（3，2），故选：B．【点评】本题考查了关于y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．5．【分析】根据不等式的性质进行判断．【解答】解：A、若a＞|b|，则a2＞b2，正确；B、若a＞b，当a＝1，b＝﹣2，时则＞，错误；C、若a＞b，当c2＝0时则ac2＝bc2，错误；D、若a＞b，c＞d，如果a＝1，b＝﹣1，c＝﹣2，d＝﹣4，则a﹣c＝b﹣d，错误；故选：A．【点评】考查了不等式的性质．要认真弄清不等式的基本性质与等式的基本性质的异同，特别是在不等式两边同乘以（或除以）同一个数时，不仅要考虑这个数不等于0，而且必须先确定这个数是正数还是负数，如果是负数，不等号的方向必须改变．6．【分析】设正多边形的中心角的度数是x，根据弧长公式即可求得x的值，然后利用360度除以x即可得到．【解答】解：设正多边形的中心角的度数是x，根据题意得：＝π，解得：x＝10．则n＝＝36．故选：C．【点评】本题考查了正多边形的计算以及扇形的弧长公式，正确求得中心角的度数是关键．7．【分析】方程的另一个根为a，根据根与系数的关系得出﹣2a＝﹣2，求出即可．【解答】解：设方程的另一个根为a，∵关于x的方程x2+kx﹣2＝0的一个根是﹣2，∴﹣2a＝﹣2，解得：a＝1，故选：B．【点评】本题考查了一元二次方程的解和根与系数的关系，能熟记根与系数的关系内容是解此题的关键．8．【分析】连接OA，根据垂径定理求出AE，根据勾股定理得出方程，求出方程的解即可．【解答】解：设DE为x，连接OA，∵CD是⊙O的直径，弦AB⊥CD于点E，AB＝24，∴∠AEO＝90°，AE＝EB＝12，由勾股定理得：OA2＝AE2+OE2，132＝122+（13﹣x）2，解得：x＝8，则DE的长度是8，故选：D．【点评】本题考查了垂径定理和勾股定理的应用，能求出AE＝EB是解此题的关键，注意：垂直于弦的直径平分弦．9．【分析】作AD⊥BC于D，根据速度和时间先求得AC的长，在Rt△ACD中，求得∠ACD的度数，再求得AD的长度，然后根据∠B＝30°求出AB的长．【解答】解：如图，过点A作AD⊥BC，垂足为D，在Rt△ACD中，∠ACD＝75°﹣30°＝45°，AC＝30×25＝750（米），∴AD＝AC•sin45°＝375（米）．在Rt△ABD中，∵∠B＝30°，∴AB＝2AD＝750（米）．故选：A．【点评】本题考查了解直角三角形的应用，解答本题的关键是根据仰角和俯角构造直角三角形并解直角三角形，难度适中．10．【分析】根据图象得出a＞0，b＝2a＞0，c＜0，即可判断①②；把x＝2代入抛物线的解析式即可判断③，求出点（﹣5，y1）关于对称轴的对称点的坐标是（3，y1），根据当x＞﹣1时，y 随x的增大而增大即可判断④．【解答】解：∵二次函数的图象的开口向上，∴a＞0，∵二次函数的图象y轴的交点在y轴的负半轴上，∴c＜0，∵二次函数图象的对称轴是直线x＝﹣1，∴﹣＝﹣1，∴b＝2a＞0，∴abc＜0，∴①正确；2a﹣b＝2a﹣2a＝0，∴②正确；∵二次函数y＝ax2+bx+c图象的一部分，其对称轴为x＝﹣1，且过点（﹣3，0）．∴与x轴的另一个交点的坐标是（1，0），∴把x＝2代入y＝ax2+bx+c得：y＝4a+2b+c＞0，∴③错误；∵二次函数y＝ax2+bx+c图象的对称轴为x＝﹣1，∴点（﹣5，y1）关于对称轴的对称点的坐标是（3，y1），根据当x＞﹣1时，y随x的增大而增大，∵＜3，∴y2＜y1，∴④正确；故选：C．【点评】本题考查了二次函数的图象与系数的关系的应用，题目比较典型，主要考查学生的理解能力和辨析能力．11．【分析】如图，利用平行四边形的性质得AD＝BC＝4，AD∥BC，则∠2＝∠3，再利用旋转的性质得∠1＝∠2，AB＝AE，接着证明∠AEB＝∠DAB得到DB＝DA＝4，然后证明△BAE∽△BDA，最后利用相似比计算AB的长．【解答】解：如图，∵四边形ABCD为平行四边形，∴AD＝BC＝4，AD∥BC∴∠2＝∠3，∵平行四边形ABCD绕点A旋转到平行四边形AEFG的位置，点B，E，D，F在同一直线上，∴∠1＝∠2，AB＝AE，∴∠1＝∠3，∠4＝∠AEB，而∠AEB＝∠3+∠DAE，∴∠AEB＝∠DAB＝∠4，∴DB＝DA＝4，而点E为BD的中点，∴BE＝2，∵∠1＝∠3，∠4为公共角，∴△BAE∽△BDA，∴AB：BD＝BE：BA，即AB：4＝2：AB，∴AB＝2．故选：C．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了平行四边形的性质和相似三角形的判定与性质．12．【分析】根据第10号箱子得球的颜色可得出，其颜色按“红、绿、黄”三个一循环进行循环，结合2018＝3×672+2可得出：当他围绕圆桌刚好丢完2018圈时，则第10号箱子有673个红球、673个绿球、672个黄球，此题得解．【解答】解：第1圈第10号箱子丢进的为红球，第2圈第10号箱子丢进的为绿球，第3圈第10号箱子丢进的为黄球，第4圈第10号箱子丢进的为红球，…，即第10号箱子得球颜色分别为：红、绿、黄、红、绿、黄、红、…，∵2018＝3×672+2，∴2018个球中有673个红球、673个绿球、672个黄球．故选：B．【点评】本题考查了规律型中图形的变化类，根据箱子里面得球颜色的变化找出变化规律是解题的关键．二、填空题（本大题共6小题，每小题3分，共18分）13．【分析】原式利用十字相乘法分解即可．【解答】解：原式＝（x﹣3）（x﹣6），故答案为：（x﹣3）（x﹣6）【点评】此题考查了因式分解﹣十字相乘法，熟练掌握十字相乘的方法是解本题的关键．14．【分析】首先运用平行线的性质求出∠AOB的大小，然后借助平角的定义求出∠3即可解决问题．【解答】解：如图，∵直线l4∥l1，∴∠1+∠AOB＝180°，而∠1＝124°，∴∠AOB＝56°，∴∠3＝180°﹣∠2﹣∠AOB＝180°﹣88°﹣56°＝36°，故答案为：36°．【点评】此题主要考查了平行线的性质及其应用问题；应牢固掌握平行线的性质，这是灵活运用、解题的基础和关键．15．【分析】根据题意画出树状图，再根据树状图即可求得所有等可能的结果与两次取出的小球颜色相同的情况，然后根据概率公式求解．【解答】解：画树状图如下：由树状图可知，共有20种等可能结果，其中取出的小球颜色相同的有8种结果，∴两次取出的小球颜色相同的概率为＝，故答案为：【点评】此题考查了树状图法与列表法求概率．解题的关键是根据题意列表或画树状图，注意列表法与树状图法可以不重不漏的表示出所有等可能的结果．用到的知识点为：概率＝所求情况数与总情况数之比．16．【分析】作AC⊥OB、O′D⊥A′B，由点A、B坐标得出OC＝3、AC＝、BC＝OC＝3，从而知tan∠ABC＝＝，由旋转性质知BO′＝BO＝6，tan∠A′BO′＝tan∠ABO＝＝，设O′D＝x、BD＝3x，由勾股定理求得x的值，即可知BD、O′D的长即可得．【解答】解：如图，过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，∵A（3，），∴OC＝3，AC＝，∵OB＝6，∴BC＝OC＝3，则tan∠ABC＝＝，由旋转可知，BO′＝BO＝6，∠A′BO′＝∠ABO，∴＝＝，设O′D＝x，BD＝3x，由O′D2+BD2＝O′B2可得（x）2+（3x）2＝62，解得：x＝或x＝﹣（舍），则BD＝3x＝，O′D＝x＝，∴OD＝OB+BD＝6+＝，∴点O'的坐标为（，），故答案为：（，）．【点评】本题考查了坐标与图形变化﹣旋转，主要利用了勾股定理、解直角三角形，熟记性质并作辅助线构造出直角三角形是解题的关键．17．【分析】先证明△ABC是等边三角形，得AC＝BC＝6，证明△AOE∽△COB，则＝，得OC＝4，再证明△OFC∽△AEC，则，得OF＝2，由平行线分线段成比例线段定理可得结论．【解答】解：∵四边形ABCD是菱形，∴AB＝BC＝AD＝6，∵∠ABC＝60°，∴△ABC是等边三角形，∴AC＝BC＝6，∵E是AD的中点，∴AE＝AD＝3，∵AD∥BC，∴△AOE∽△COB，∴＝，∴AO＝2，OC＝4，∵OF∥BC，BC∥AD，∴OF∥AE，∴△OFC∽△AEC，∴，∴，OF＝2，∵OF∥BC，∴，∴，∵OM +MC ＝4， ∴OM ＝1． 故答案为：1．【点评】本题考查了相似三角形的判定和性质，平行线分线段成比例定理，等边三角形的判定等知识，依次得AO 、OC 、OM 、MC 的关系是解题的关键．18．【分析】先过点C 作CE ⊥OA ，CF ⊥OD ，可知四边形CEOF 是矩形，然后根据△OAC 的面积求出CE 的长度，进而求出三角形OCD 与三角形OAD 的面积，最后根据割补求出△ACD 的面积． 【解答】解：过点C 作CE ⊥OA 于点E ，CF ⊥OD 于点F ． ∵AB 为⊙P 直径， ∴∠AOB ＝90°， ∴四边形CEOF 是矩形， ∴∠OEC ＝90°，CF ＝OE ，∵OA ＝OC ＝OD ＝5，△OAC 的面积为12∴，即，∴，在Rt △OCE 中，＝，∴∴，，∴S △ACD ＝S △OAC +S △OCD ﹣S △OAD ＝，故答案为3．【点评】本题考查了圆与正方形的相关知识，正确运用勾股定理和割补三角形面积是解题的关键．三、解答题（本大题共7小题，共计86分）19．【分析】（1）先化简二次根式、计算负整数指数幂、零指数幂、代入三角函数值，再依次计算乘法、加减运算即可得；（2）先根据分式混合运算顺序和运算法则化简原式，再将x的值代入计算即可得．【解答】解：（1）原式＝3﹣﹣1﹣4×＝3﹣﹣1﹣2＝﹣；（2）原式＝•＝＝．【点评】本题考查了实数的混合运算与分式的化简求值．解题的关键是对分式的分子分母因式分解及分式混合运算顺序和运算法则．20．【分析】（1）根据选C的有50人，占50%，从而可以求得本次本次接受问卷调查的人数以及在扇形统计图中“D”选项所占的百分比；（2）根据条形统计图中选B的人数和（1）求得的调查的总人数可以求得扇形统计图中，“B”选项所对应扇形圆心角的度数；（3）根据题意可以求得选A的人数，从而可以将条形统计图补充完整；（4）根据统计图中的数据可以求得该小区使用共享单车的时间在“A”选项的有多少人．【解答】解：（1）由题意可得，本次接受问卷调查的有：50÷50%＝100（人），在扇形统计图中“D”选项所占的百分比为：×100%＝10%，故答案为：100，10%；（2）由题意可得，扇形统计图中，“B”选项所对应扇形圆心角为：360°×＝72°，故答案为：72；（3）选A的有：100﹣20﹣50﹣10＝20，补全的条形统计图如右图所示；（4）由题意可得，该小区使用共享单车的时间在“A”选项的有：1200×＝240（人），即该小区使用共享单车的时间在“A”选项的有240人．【点评】本题考查条形统计图、用样本估计总体、扇形统计图，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．21．【分析】（1）由AE＝FB＝x知EF＝60﹣2x，据此得包装盒的高为×（60﹣2x）＝（30﹣x），根据题意列出方程，解之可得；（2）由AE＝x知包装盒的宽为x，从而得出包装盒的侧面积S＝x•（30﹣x）•4＝﹣8（x ﹣15）2+1800，根据二次函数的性质求解可得．【解答】解：（1）设AE＝FB＝x（cm），则EF＝60﹣2x，∴包装盒的高为×（60﹣2x）＝（30﹣x），由题意得（30﹣x）＝20，解得：x＝30﹣10；（2）∵AE＝x，∴包装盒的宽为x，则包装盒的侧面积S＝x•（30﹣x）•4＝﹣8x2+240x＝﹣8（x﹣15）2+1800，∴当x＝15时，S取得最大值．【点评】本题主要考查二次函数的应用，解题的关键是根据等腰直角三角形的性质得出包装盒的高、宽，并列出侧面积的函数解析式．22．【分析】（1）根据点A、B都在反比例函数的图象上，先计算k，再计算m，然后用待定系数法求出一次函数的解析式；（2）过点A作AD⊥BC，垂足为D，根据线段AD、BD的长，得到特殊的直角三角形：△ABD 和△ADC，从而得到点C的坐标．【解答】解：（1）因为点A、B都在反比例函数的图象上，所以k＝1×3＝3，所以反比例函数的解析式为：y1＝，当x＝﹣3时，m＝﹣1，所以点B（﹣3，﹣1）由于点A、B都在一次函数y2＝ax+b的图象上，所以，解得所以一次函数的解析式为：y2＝x+2（2）如图所示：作∠BAC＝90°，过点A作AD⊥BC，垂足为D，∵点A（1，3），点B（﹣3，﹣1），所以点D（1，﹣1）∴AD＝3﹣（﹣1）＝4，BD＝1﹣（﹣3）＝4∵AD⊥BC，∴∠BAD＝45°，又∵∠BAC＝90°，∴∠DAC＝∠C＝45°，∴AD＝CD＝4设点C（m，﹣1），∴m＝1+CD＝5．所以点C（5，﹣1）答：点C的坐标为（5，﹣1）【点评】本题考查了待定系数法确定反比例函数、一次函数解析式及等腰直角三角形的性质和判定．解决本题的关键是作AD⊥BC，构造了等腰直角三角形．23．【分析】（1）想办法证明∠DCM＝∠CAD即可解决问题；（2）连接OD交BC于H．设CD＝BD＝a．利用相似三角形的性质求出a即可解决问题；【解答】（1）证明：∵D为的中点，∴＝，∴∠DCB＝∠CAD，∵∠CDM＝∠ADC，∴△ACD∽△CMD．（2）解：连接OD交BC于H．设CD＝BD＝a．∵AB是直径，∴∠ACB＝∠ADB＝90°，∵＝，∴∠CBD＝∠DAB，OD⊥BC，∴tan∠CBD＝tan∠DAB＝＝，∴AD＝2a，∵△ACD∽△CMD，∴＝＝＝，∵AC＝3，∴CM ＝，DM ＝a ，AM ＝a ，在Rt △ACM 中，AM ＝＝＝a ，∴a ＝，∴AD ＝2，BD ＝CD ＝，在Rt △ADB 中，AB ＝＝5，∴OD ＝，∵OD ⊥BC ，∴CH ＝HB ，∵OA ＝OB ，∴OH ＝AC ＝，∴DH ＝1，在Rt △ACB 中，BC ＝＝4，∴S △BCD ＝•BC •DH ＝×4×1＝2．【点评】本题考查相似三角形的判定和性质、垂径定理、圆周角定理、勾股定理、三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造三角形中位线解决问题，学会利用参数解决问题，属于中考压轴题．24．【分析】（1）把B 点坐标代入y ＝x 2﹣ax 中求出a 的值即可得到抛物线解析式；（2）作BH ⊥x 轴于H ，如图，先解方程得到x 2﹣2x ＝0得A （2，0），利用待定系数法表示出直线BC 的解析式为y ＝（m ﹣3）x +m ，则解方程x 2﹣2x ＝（m ﹣3）x +m 得E （m ，m 2﹣2m ），根据三角形面积公式，利用S 四边形ABCD ＝S 梯形OCBH +S △OCD ﹣S △ABH 列方程得到（m +3）•1+•m •m ﹣•3•3＝25，然后解方程求出m 即可得到C 点坐标；（3）易得直线CD 的解析式为y ＝﹣x +m ，直线AB 的解析式为y ＝﹣x +2，根据平行四边形的判定方法当BC ∥AF 时，四边形ABCF 为平行四边形，则可设直线AF 的解析式为y ＝（m ﹣3）x +n ，把A （2，0）代入得2m ﹣6+n ＝0得到直线AF 的解析式为y ＝（m ﹣3）x +6﹣2m ，再解方程组得F （3，m ﹣3），然后把F （3，m ﹣3）代入y ＝x 2﹣2x 得关于m 的方程，最后解关于m 的方程即可【解答】解：（1）把B （﹣1，3）代入y ＝x 2﹣ax 得1+a ＝3，解得a ＝2，∴抛物线解析式为y ＝x 2﹣2x ；（2）作BH ⊥x 轴于H ，如图，当y ＝0时，x 2﹣2x ＝0，解得x 1＝0，x 2＝2，则A （2，0），设直线BC 的解析式为y ＝kx +m ，把B （﹣1，3）代入得﹣k +m ＝3，解得k ＝m ﹣3，∴直线BC 的解析式为y ＝（m ﹣3）x +m ，解方程x 2﹣2x ＝（m ﹣3）x +m ，整理得x 2﹣（m ﹣1）x ﹣m ＝0，解得x 1＝﹣1，x 2＝m ，∴E （m ，m 2﹣2m ），∴D （m ，0），∵S 四边形ABCD ＝S 梯形OCBH +S △OCD ﹣S △ABH ，∴（m +3）•1+•m •m ﹣•3•3＝25，整理得m 2+m ﹣56＝0，解得m 1＝7，m 2＝﹣8（舍去），∴C 点坐标为（0，7）；（3）易得直线CD 的解析式为y ＝﹣x +m ，直线AB 的解析式为y ＝﹣x +2，∴AB ∥CD ，当BC ∥AF 时，四边形ABCF 为平行四边形，而直线BC 的解析式为y ＝（m ﹣3）x +m ，∴直线AF 的解析式可设为y ＝（m ﹣3）x +n ，把A （2，0）代入得2m ﹣6+n ＝0，解得n ＝6﹣2m ，∴直线AF 的解析式为y ＝（m ﹣3）x +6﹣2m解方程组得，则F （3，m ﹣3），把F （3，m ﹣3）代入y ＝x 2﹣2x 得m ﹣3＝9﹣6，解得m ＝6，∴当m 为6时，四边形ABCF 是平行四边形．【点评】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的判定；会利用待定系数法求二次函数解析式和一次函数解析式，理解两直线平行的问题；理解坐标与图形性质．25．【分析】（1）如图1中，连接AC．只要证明AB＝BC即可解决问题；（2）如图1﹣1中，设AC交MN于G，延长MC到H，使得CH＝BM＝m．连接HN．想办法证明△NCH∽△ACB，可得＝，即＝，推出CN＝m即可解决问题；（3）如图2中，连接AC、PC、AQ，作PH∥AC交CD于H．设AC交EF于J．由△APQ∽△CHP，可得＝，想办法求出CH：PH的值即可解决问题；【解答】解：（1）如图1中，连接AC．∵A（﹣8，0），B（﹣5，4），BC∥x轴，∴AB＝＝5，BC＝5，∴AB＝BC＝5，∴∠BAC＝∠BCA，∵BC∥AD，∴∠BCA＝∠CAD，∴∠BAC＝∠CAB，∵A、D关于y轴对称，∴CA＝CD，∴∠CAD＝∠CDA＝α，∴∠BAD＝2α．（2）如图1﹣1中，设AC交MN于G，延长MC到H，使得CH＝BM＝m．连接HN．∵∠BAC＝∠BCA＝∠CAD＝∠CDA＝α，∴∠ABC＝∠ACD，∵∠AMN＝∠ABC，∴∠AMG＝∠NCG，∵∠AGM＝∠NGC，∴△AGM∽△NGC，∴＝，∴＝，∵∠MGC＝∠AGN，∴△MGC∽△AGN，∴∠ANG＝∠MCG＝α，∴∠MAN＝∠ANM＝α，∴AM＝MN，∵∠HMA＝∠HMN+∠AMN＝∠BAM+∠ABM，∴∠HMN＝∠BAM，∵AB＝BC＝MH，∴△BAM≌△HMN，∴∠H＝∠ABM，∵∠ACB＝∠NCH，∴△NCH∽△ACB，∴＝，∴＝，∴CN＝m，∴N（m，4﹣m）．（3）如图2中，连接AC、PC、AQ，作PH∥AC交CD于H．设AC交EF于J．同法可证：∠PAQ ＝∠PCH ，∵AC ∥PH ，∴∠ACH ＝∠CHP ，∵∠ACD ＝∠APQ ，∴∠APQ ＝∠CHP ，∴△APQ ∽△CHP ，∴＝，易知E （﹣6，），F （，），J （﹣，），∴FJ ＝，EF ＝，∵＝t ，∴PF ＝， ∵PH ∥CJ ，∴FH ：FC ＝PF ：FJ ＝：＝13：8t ，∴FH ：CH ＝13：（13+8t ）∵CJ ＝CF ，∴∠CJF ＝CFJ ＝∠HPF ＝∠PFH ，∴HP ＝HF ，∴PH ：CH ＝13：（1+8t ），∴PA ：PQ ＝CH ：PH ＝（13+8t ）：13．【点评】本题考查相似三角形综合题、平行线的性质、等腰三角形的判定和性质、相似三角形的判定和性质、轴对称图形的性质等知识，解题的关键是学会添加常用辅助线构造相似三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．。

保密*启用前 [考试时间：2018年1月18日上午9：00—11：30]绵阳市高中2018级第二次诊断性考试理科综合能力测试本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分，两卷共8页。

满分300分，考试时间150分钟。

第L卷答案涂在答题卡上，第Ⅱ卷答案写在答题卷上。

第Ⅰ卷(选择题，共126分)注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考试科目用4B或5B铅笔准确涂写在答题卡上，同时将第Ⅱ卷答卷密封线内的项目填写清楚。

2，第1卷每小题选出答案后，用4B或5B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，．用橡皮擦擦干净后，再选涂其它答案，不能答在试题卷上。

3．可能用到的相对原子质量：H1 C12 N14 O16一、选择题(本题包括13小题。

每小题只有一个选项符合题意．每小题6分)1．科学家在研究分泌蛋白的合成和分泌时，向豚鼠的胰脏腺泡细胞中注射3H标记的亮氨酸，经过一段时间后，被标记的氨基酸可依次出现在该细胞的不同部位。

下面有关叙述哪一项是正确的?A．被标记的氨基酸首先出现在附着有核糖体的内质网中B．连接图中①、②、③、④所示结构的是具膜的小泡C．图中②、③、④分别代表内质网、高尔基体、细胞膜D．细胞内的各种生物膜既各施其职，又有紧密的联系，2．下面是在不同温度条件下测定某种植物光合作用与呼吸作用的强度绘制成的曲线。

如果在光照强度相同时，对植物生长最有利的温度是A．t0～t1B．t1～t2C．t2～t3D．t3～t43．下面是将某动物体(XY型)的性腺制成切片后，在显微镜下观察到的细胞分裂时期示意图。

比较甲、乙两个细胞所处的分裂时期，可以得出下列哪一项结论？A．它们处于同一细胞周期的不同阶段B．都可发生基因突变和基因重组C．只有甲图发生了X和Y染色体的分离D．乙图细胞分裂的结果染色体数且减半4．在人体特异性免疫反应中，体液免疫与细胞免疫的关系是A．只有体液免疫才需要抗体的参与，只有细胞免疫才需要淋巴细胞的参与B．体液免疫和细胞免疫分别组成人体内防止病原体入侵的第二、第三道防线C．对侵入人体的病原体由体液免疫发挥作用，—对癌细胞由细胞免疫发挥作用D．在抗病毒感染中，往往先通过体液免疫发挥作用，再通过细胞免疫发挥作用一5．下面有关真核细胞基因结构和功能的叙述哪一项是错误的?A．等位基因A与a的最本质区别是两者的碱基排列顺序不同B．对血友病患者的造血干细胞进行基因改造后，其遗传性发生改变C．不同种类的蛋白质的基因所含外显子和内含子的数目是不同的D．用PCR技术进行DNA的体外扩增时要发生碱基互补配对6．等物质的量的下列物质分别与足量的NaOH溶液完全反应，需要NaOH的量最多的是A．NaHS18 B．AICl3C．SiO2D．7.某货车由于制动失灵冲人高速公路边的小河沟内，车上装载的化工原料遇水着火燃烧，该化工原料可能是A．NH4N18 B．KCl18C．CaC2D．CaO8.设NA表示阿伏加德罗常数的值，下列叙述正确的是A．0．8gNH2—所含电子数为N AB．在44g干冰中，含C=O键数为4N AC．1molSi02晶体中含有2N A个Si—O键D．常温常压下，48g臭氧所含分子数为N A9．下列实验方案合理的是A．蔗糖水解(H2S18作催化剂)后，在水解液中加新制的Cu(OH)2悬浊液加热煮沸检验水解产物B．用氨水清洗做过银镜反应的试管C．除去苯中的苯酚，加饱和NaHC18溶液再分液D．用新制的生石灰，通过加热蒸馏，以除去乙醇中的少量水10．广义的水解观认为：无论是盐的水解还是非盐的水解，其最终结果是：反应中各物质和水分别解离成两部分，然后两两重新组合成新的物质。

生物试题参考答案及评分标准说明：1．生物学专有名词和专业术语．．．．．．．．出现错字、别字、改变了原含义等，扣1分/字（或不得分）。

2．除参考答案外，其它合理答案应酌情给分。

选择题（36分）1---6C B D C A D非选择题（54分）29.（8分）(1)细胞代谢（2分）(2)细胞分化（1分）信息交流（1分）(3)生命活动的主要承担者都是蛋白质；遗传信息的携带者都是DNA（核酸）；都以ATP作为直接能源物质；膜的主要组成成分都是磷脂和蛋白质；都能通过葡萄糖的氧化分解获得能量；都共用一套密码子翻译；都通过转录和翻译过程表达遗传信息等（2+2分）30.（10分）（1）各种化学物质的含量和理化性质（2分）（2）Na+（2分）主动运输（2分）（3）不认同（1分）血浆中存在缓冲物质，可以将吸收的酸性物质中和，血浆pH不会发生明显改变；如果为软化血管而过量摄入酸性物质导致血浆PH发生明显改变反而会危及健康（3分）31.（9分）（1）促甲状腺激素释放激素（2分）下丘脑（2分）（2）促进（1分）抑制（1分）（3）给该病人注射适量的TSH，其血液中的TRH含量将下降到正常值，甲状腺激素含量将升高到正常值（1+1+1=3分）32.（12分）（1）反转录（2分）（2）①1/2（2分）②两条非同源染色体上（2分）③分别位于Z、W染色体上（2分）F 1个体随机交配，统计F2中的普通型家蚕的性别。

如果F2中普通型家蚕中雌雄均有，则基因的位置为a；如F2中普通型家蚕中只有雄性，则基因的位置为b。

（1+1+1+1=4分）或（F1个体随机交配，统计F2中耐热型家蚕的性别比例，如果F2中耐热型家蚕中雌：雄=1:1，则基因的位置为a；如F2中耐热型家蚕中雌：雄=2:1，则基因的位置为b。

）或（F1个体随机交配，统计F2中家蚕的表现型及比例，如果F2中耐热雄：耐热雌：普通雄：普通雌=3:3:1:1，则基因的位置为a；如F2中耐热雌：耐热雄：普通雄=2:1:1，则基因的位置为b。

绵阳南山中学高2021届高三“二诊〞热身考试数学〔理科〕第一卷〔共60分〕一、选择题：本大题共12个小题,每题5分,共60分．在每题给出的四个选项中，只有一项为哪一项符合题目要求的．1. 设集合，，那么〔〕A. B. C. D.【答案】C【解析】=因为所以应选C2. 是虚数单位，复数的共轭复数虚部为〔〕A. B. -4 C. 3 D. 4【答案】B【解析】=，所以共轭复数为即虚部为-4应选B3. 某中学有高中生3500人，初中生1500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为的样本，从高中生中抽取70人，那么为〔〕A. 100B. 150C. 200D. 250【答案】A【解析】试题分析：根据可得：，应选择A考点：分层抽样视频4. 下边程序框图的算法思路源于我国古代数学名著?九章算术?中的“更相减损术〞，执行该程序框图，假设输出的，那么输入的可能是〔〕A. 15,18B. 14,18C. 12,18D. 9,18【答案】B【解析】根据题意，执行程序后输出的a=2，那么执行该程序框图前，输人a、b的最大公约数是2，分析选项中的四组数，满足条件的是选项B应选B5. ，直线与直线互相垂直，那么的最小值为〔〕A. 1B. 2C.D.【答案】B【解析】b＞0，两条直线的斜率存在，因为直线〔b2+1〕x+ay+2=0与直线x一b2y一1=0互相垂直，所以〔b2+1〕-ab2=0，ab=b+≥2应选B6. 在中，分别为所对的边，假设函数有极值点，那么的最小值是〔〕A. 0B.C.D. -1【答案】D【解析】，∴f′〔x〕=x2+2bx+〔a2+c2-ac〕，又∵函数有极值点，∴x2+2bx+〔a2+c2-ac〕=0有两个不同的根，∴△=〔2b〕2-4〔a2+c2-ac〕＞0，即ac＞a2+c2-b2，即ac＞2accosB；即cosB＜，故∠B的范围是〔所以，当时的最小值是-1应选D7. 某学校需要把6名实习老师安排到三个班级去听课，每个班级安排2名老师，甲不能安排到班，乙和丙不能安排到同一班级，那么安排方案的种数有〔〕A. 24B. 36C. 48D. 72【答案】C【解析】先考虑甲不能到A班的方案：种，减去其中乙和丙安排到同一班级的方案：种，即48种；应选C8. 以下四个命题中：①某地市高三理科学生有15000名，在一次调研测试中，数学成绩服从正态分布，，假设按成绩分层抽样的方式抽取100分试卷进行分析，那么应从120分以上〔包括120分〕的试卷中抽取15分；②命题，，那么，；③在上随机取一个数，能使函数在上有零点的概率为；④在某次飞行航程中遭遇恶劣气候，用分层抽样的20名男乘客中有5名晕机，12名女乘客中有8名晕机，在检验这些乘客晕机是否与性别有关时，采用独立性检验，有97%以上的把握认为与性别有关.0.15 0.1 0.05 0.0252.072 2.7063.841 5.024其中真命题的序号为〔〕A. ①②③B. ②③④C. ①②④D. ①③④【答案】B【解析】对于①，在一次调研测试中，数学成绩ξ服从正态分布N〔100，σ2〕，∴数学成绩ξ关于ξ=100对称，∵P〔80＜ξ≤100〕=0.40，∴P〔ξ＞120〕=P〔ξ＜80〕=0.5-0.40=0.1，那么该班数学成绩在120分以上的人数为0.1×100=10，故①错误；对于②，命题p：∀x∈R，sinx≤1，那么￢p：∃x∈R，sinx＞1，故②正确；对于③，由()2−8≥0，解得m≤-2或m≥2，∴在[-4，3]上随机取一个数m，能使函数在R上有零点的概率为，故③正确；对于④，填写2×2列联表如下：晕机不晕机合计男乘客 5 15 20女乘客8 4 12合计13 19 32那么k2的观测值k＝有97%以上的把握认为晕机与性别有关.故④对应选B9. 某车间加工零件的数量与加工时间的统计数据如表：零件数〔个〕10 20 30加工时间〔分钟〕21 30 39现已求得上表数据的线性回归方程中的值为0.9，那么据此回归模型可以预测，加工100个零件所需要的加工时间约为〔〕A. 84分钟B. 94分钟C. 102分钟D. 112分钟【答案】C【解析】试题分析：,,回归直线过样本点的中心，，解得，加工100个零件大约需要分钟.考点：回归直线方程的应用.10. 假设圆上至少有三个不同的点到直线的距离为，那么直线的斜率的取值范围是〔〕A. B.C. D.【答案】B【解析】圆可化为那么圆心为〔-2，2〕，半径为3，那么由圆x2+y2+4x-4y-10=0上至少有三个不同点到直线l：ax+by=0的距离为2，那么圆心到直线l：ax+by=0的距离d≤32=即那么a2+b2-4ab≤0，假设b=0，那么a=0，故不成立，故b≠0，那么上式可化为1+由直线l的斜率k=-那么上式可化为k2+4k+1≤0解得应选B11. 如图，分别是双曲线的左、右焦点，过的直线与双曲线分别交于点，假设为等边三角形，那么双曲线的方程为〔〕A. B.C. D.【答案】C【解析】根据双曲线的定义，可得|AF1|-|AF2|=2a，∵△ABF2是等边三角形，即|AF2|=|AB|∴|BF1|=2a又∵|BF2|-|BF1|=2a，∴|BF2|=|BF1|+2a=4a，∵△BF1F2中，|BF1|=2a，|BF2|=4a，∠F1BF2=120°∴|F1F2|2=|BF1|2+|BF2|2-2|BF1|•|BF2|cos120°即4c2=4a2+16a2-2×2a×4a×〔-〕〕=28a2，解得c2=7a2，又c=所以方程为应选C点睛：此题主要考查双曲线的定义和简单几何性质，考查了余弦定理解三角形，根据条件求出a，b的关系是解决此题的关键．12. 函数，有三个不同的零点，〔其中〕，那么的值为〔〕A. B. C. -1 D. 1【答案】D【解析】令f〔x〕=0，别离参数得a=令h〔x〕=由h′〔x〕=得x=1或x=e．当x∈〔0，1〕时，h′〔x〕＜0；当x∈〔1，e〕时，h′〔x〕＞0；当x∈〔e，+∞〕时，h′〔x〕＜0．即h〔x〕在〔0，1〕，〔e，+∞〕上为减函数，在〔1，e〕上为增函数．∴0＜x1＜1＜x2＜e＜x3，a=令μ=那么a=即μ2+〔a-1〕μ+1-a=0，μ1+μ2=1-a＜0，μ1μ2=1-a＜0，对于μ=，那么当0＜x＜e时，μ′＞0；当x＞e时，μ′＜0．而当x＞e时，μ恒大于0．不妨设μ1＜μ2，那么μ1=，=〔1-μ1〕2〔1-μ2〕〔1-μ3〕=[〔1-μ1〕〔1-μ2〕]2=[1-〔1-a〕+〔1-a〕]2=1．应选D．点睛：此题考查了利用导数研究函数单调性，极值等性质，训练了函数零点的判断方法，运用了别离变量法，换元法，函数构造法等数学转化思想方法，综合性强．第二卷〔共90分〕二、填空题〔每题5分，总分值20分，将答案填在答题纸上〕13. 的展开式中，的系数为，那么__________．【答案】4【解析】，所以由得，从而点睛：求二项展开式有关问题的常见类型及解题策略(1)求展开式中的特定项.可依据条件写出第项，再由特定项的特点求出值即可.(2)展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第项，由特定项得出值，最后求出其参数.14. 在一场比赛中，某篮球队的11名队员共有9名队员上场比赛，其得分的茎叶图如下图，从上述得分超过10分的队员中任取2名，那么这2名队员的得分之和超过35分的概率为__________．【答案】【解析】从得分超过10分的队员中任取2名，一共有以下10种不同的取法：(12,14)，(12,15)，(12,20)，(12,22)，(14,15)，(14,20)，(14,22)，(15,20)，(15,22)，(20,22)，其中这2名队员的得分之和超过35分的取法有以下3种：(14,22)，(15,22)，(20,22)，故所求概率P ＝.点睛：古典概型中根本领件数的探求方法(1)列举法.(2)树状图法：适合于较为复杂的问题中的根本领件的探求.对于根本领件有“有序〞与“无序〞区别的题目，常采用树状图法.(3)列表法：适用于多元素根本领件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法：适用于限制条件较多且元素数目较多的题目.15. 在中，角所对的边分别为，且，是的中点，且，，那么的最短边的边长为__________．【答案】【解析】因为，所以sinB=又∴正弦定理化简可得：sinAcosCsinA+sinAsinCcosA=sinC．即sinA〔cosCsinA+sinCcosA〕=sinC∴sinAsinB=sinC∵A+B+C=π，∴C=π-〔A+B〕∴sinAsinB=sin〔A+B〕，sinA=×sinAcosB+cosAsinB，∴sinA=cosA．即tanA=1，∵0＜A＜π，D是AC的中点，且cosB=∴A=，根据余弦定理得c2+b2-bc=26，sinA=sinC，且sinB×=sinC，的最短边的边长为故答案为16. 在平面直角坐标系中，为坐标原点，点，平面向量满足：，那么对任意的实数和任意满足条件的向量，的最小值__________．【答案】【解析】设C由得,=等价于圆M:上一点与函数图象上一点的距离，可先求圆心M到曲线上一点的距离最小值减去半径即为所求，在曲线上取点P在点P处切线斜率为，当MP垂直于切线时即可满足题意，即令那么有令在递增，且点P此时MP=，所以所求最小值为故答案为点睛：此题考查了向量数量积的坐标表示，考查了利用点点距离求最小值，利用了构造函数法，线与线垂直的应用，综合性强,属于难题,三、解答题〔本大题共6小题，共70分．解容许写出文字说明、证明过程或演算步骤．〕17. 等差数列中，公差，，且成等比数列.〔1〕求数列的通项公式；〔2〕假设为数列的前项和，且存在，使得成立，求的取值范围.【答案】(1) (2)【解析】试题分析：〔1〕由题意可得解得即可求得通项公式(2),裂项相消求和，因为存在，使得成立，所以存在，使得成立，即存在，使得成立.求出的最大值即可解得的取值范围.试题解析：〔1〕由题意可得即又因为，所以所以.〔2〕因为，所以.因为存在，使得成立，所以存在，使得成立，即存在，使得成立.又〔当且仅当时取等号〕.所以，即实数的取值范围是.18. “中国人均读书4.3本〔包括网络文学和教科书〕，比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多，是世界上人均读书最少的国家.〞这个论断被各种媒体反复引用，出现这样的统计结果无疑是令人为难的，而且和其他国家相比，我国国民的阅读量如此之低，也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站，由于不同年龄段需看不同类型的书籍，为了合理配备资源，现对小区内看书人员进行年龄调查，随机抽取了一天40名读书者进行调查，将他们的年龄分成6段：，，，，，后得到如下图的频率分布直方图.问：〔1〕估计在40名读书者中年龄分布在的人数；〔2〕求40名读书者年龄的平均数和中位数；〔3〕假设从年龄在的读书者中任取2名，求这两名读书者年龄在的人数的分布列及数学期望.【答案】(1)30;(2)54,55;(3) 的分布列如下：0 1 2数学期望【解析】试题分析：〔1〕由频率分布直方图知年龄在[40，70〕的频率为〔0.020+0.030+0.025〕×10，进而得出40 名读书者中年龄分布在[40，70〕的人数．〔2〕40 名读书者年龄的平均数为25×0.05+35×0.1+45×0.2+55×0.3+65×0.25+75×0.1．计算频率为处所对应的数据即可得出中位数．〔3〕年龄在[20，30〕的读书者有2人，年龄在[30，40〕的读书者有4人，所以X的所有可能取值是0，1，2．利用超几何分布列计算公式即可得出．........................试题解析：〔1〕由频率分布直方图知年龄在的频率为，所以40名读书者中年龄分布在的人数为.〔2〕40名读书者年龄的平均数为.设中位数为，那么解得，即40名读书者年龄的中位数为55.〔3〕年龄在的读书者有人，年龄在的读书者有人，所以的所有可能取值是0,1,2，，，，的分布列如下：0 1 2数学期望.19. 函数的图象关于直线对称，且图象上相邻两个最高点的距离为.〔1〕求和的值；〔2〕假设，求得值.【答案】(1) (2)【解析】试题分析：〔1〕由两个相邻的最高点的距离可求得周期，那么，函数为，由函数关于直线对称，可知，结合可求得的值；〔2〕对进行三角恒等变换，可求得的值，又为锐角，可求得，再利用三角恒等变换求得值.试题解析：〔1〕由题意可得函数的最小正周期为，再根据图象关于直线对称，可得结合，可得〔2〕再根据考点：三角函数的周期与初相，三角恒等变换.视频20. 如图，抛物线的焦点为，椭圆的中心在原点，为其右焦点，点为曲线和在第一象限的交点，且.〔1〕求椭圆的标准方程；〔2〕设为抛物线上的两个动点，且使得线段的中点在直线上，为定点，求面积的最大值.【答案】(1) (2) 面积的最大值为.【解析】试题分析：〔1〕由得，跟据抛物线定义，得，所以点；据椭圆定义，得．所以椭圆的标准方式是．〔2〕因为为线段的中点，得直线的方程为；联立，得，由弦长公式和点到直线的距离，得．再根据函数的单调性得面积的最大值为．试题解析：〔1〕设椭圆的方程为，半焦距为．由，点，那么．设点，据抛物线定义，得．由，，那么．从而，所以点．设点为椭圆的左焦点，那么，．据椭圆定义，得，那么．从而，所以椭圆的标准方式是．〔2〕设点，，，那么．两式相减，得，即．因为为线段的中点，那么．所以直线的斜率．从而直线的方程为，即．联立，得，那么．所以．设点到直线的距离为，那么．所以．由，得．令，那么．设，那么．由，得．从而在上是增函数，在上是减函数，所以，故面积的最大值为．考点：1、抛物线的定义；2、椭圆的方程；3、最值问题．【方法点睛】此题考查抛物线的定义和简单几何性质、待定系数法求椭圆的标准方程、直线和椭圆相交中的有关中点弦的问题，综合性强，属于难题；对于直线和圆锥曲线相交中的中点弦问题，解决此类题目的最有效方法是点差法，两式直接相减就可以表示出斜率；而第二问中面积公式求出后，函数单调性的研究更是加深了此题的难度，运算量也比拟大，不容易拿高分．21. 函数〔且〕〔1〕假设，求函数的单调区间；〔2〕当时，设，假设有两个相异零点，求证：.【答案】(1) 当时，函数的单调增区间是，单调减区间是，当时，函数的单调增区间是，单调减区间是.(2)见解析.【解析】试题分析：〔1〕由知分，两种情况讨论即得解〔2〕，设的两个相异零点为，设，因为，，所以，，相减得，相加得.要证，即证，即，即，换元设上式转化为.构造函数求导研究单调性即可得证.试题解析：〔1〕由知当时，函数的单调增区间是，单调减区间是，当时，函数的单调增区间是，单调减区间是.〔2〕，设的两个相异零点为，设，∵，，∴，，∴，.要证，即证，即，即，设上式转化为.设，∴，∴在上单调递增，∴，∴，∴.点睛：此题考查了利用导数研究函数单调性，考查了分类讨论的思想，考查了不等式的证明，利用零点的式子进行变形，采用变量集中的方法构造新函数即可证明，综合性强属于中档题请考生在22、23两题中任选一题作答，如果多做，那么按所做的第一题记分．22. 选修4-4：坐标系与参数方程在平面直角坐标系中，直线的参数方程为〔为参数〕，以原点为极点，轴正半轴为极轴建立极坐标系，曲线的方程为，定点，点是曲线上的动点，为的中点.〔1〕求点的轨迹的直角坐标方程；〔2〕直线与轴的交点为，与曲线的交点为，假设的中点为，求的长.【答案】(1) (2)【解析】试题分析：〔1〕求出曲线C1的直角坐标方程为，设点N〔x′，y′〕，Q〔x，y〕，由中点坐标公式得，由此能求出点Q的轨迹C2的直角坐标方程．〔2〕的坐标为，设的参数方程为，〔为参数〕代入曲线的直角坐标方程得，根据韦达定理，利用t的参数意义得即可得解.试题解析：〔1〕由题意知，曲线的直角坐标方程为.设点，，由中点坐标公式得，代入中，得点的轨迹的直角坐标方程为.〔2〕的坐标为，设的参数方程为，〔为参数〕代入曲线的直角坐标方程得：，设点对应的参数分别为，那么，，.23. 选修4-5：不等式选讲函数，.〔1〕求不等式的解集；〔2〕假设方程有三个实数根，求实数的取值范围.【答案】(1) (2)【解析】试题分析：〔1〕通过讨论的范围，得到关于的不等式组，求出不等式的解集即可；〔2〕别离，得到，令，结合函数的图象求出的范围即可．试题解析：〔1〕原不等式等价于或或，得或∴不等式的解集为.〔2〕由方程可变形为，令，作出图象如下：于是由题意可得.点睛：此题考查了利用分类讨论思想解绝对值不等式问题，考查数形结合思想处理方程的根的个数问题，是一道中档题．。

秘密★启用前【考试时间：2018年1月6日上午9∶00～11∶30】绵阳市高中2018级高三第二次诊断性考试理科综合能力测试可能用到的相对原子质量：H 1 C 12 O 16 S 32 Cu 64 Zn 65 Ba 137第Ⅰ卷二、选择题：本题共8小题，每小题6分。

在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

14. 2018年10月17日，我国用长征二号FY11运载火箭将“神舟十一号”飞船送入预定转移轨道。

关于火箭发射，下列说法正确的是A.火箭刚离开发射架时，火箭处于失重状态B.火箭刚离开发射架时，火箭处于超重状态C．火箭发射时，喷出的高速气流对火箭的作用力大于火箭对气流的作用力D.火箭发射时，喷出的高速气流对火箭的作用力小于火箭对气流的作用力15. 2018年7月，科学家宣布找到了一颗人类“宜居”行星，它是离太阳最近的恒星——比邻星( Proxima Centauri)的行星。

若这颗“宜居”行星质量为地球的a倍，半径为地球的b倍。

设该行星的卫星的最小周期为T1，地球的卫星的最小周期为T2，则T1 /T2=16.在2018年11月初的珠海航展上，我国展出了国产四代战机———歼-20等最先进飞机。

假设航展飞行表演中，两架完全相同的歼-20飞机甲、乙在两条平行平直跑道上同向滑行，在0～t2时间内的v-t图像如图所示，则A.在t l时刻，两飞机沿跑道方向相距最远B.在t l时刻，两飞机发动机输出功率相等C. 0～t2，飞机甲的平均速度大于飞机乙的平均速度D.0～t2，合外力对飞机甲做的功大于合外力对飞机乙做的功17.如图所示的电路中，E为电源电动势，r为电源内阻，R1和R2为定值电阻，R为滑动变阻器。

当R的滑片P在某一位置时，闭合开关S，电压表的读数为U=l.00 V，电流表A1的读数I1=0.80A，电流表A2的读数为I2=1.20A。

四川绵阳南山中学2018届高三理综二诊试卷（含答案）秘密★启用前2018年1月绵阳南山中学2017年秋季高2018届二诊热身理科综合试题命题人（审题人）：物理：邓旭（王斌）化学：王大志（李林）生物：粟洋（吴文兴）注意事项：1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

答题前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第I卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3．回答第II卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试题和答题卡一并交回。

可能用到的相对原子质量：C12H1O16Na23S32Mo96Pb207Co59Al27第Ⅰ卷（选择题共126分）本卷共21小题，每小题6分，共126分。

一、选择题：本大题共13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列关于真核细胞与原核细胞的相关叙述，正确的是A．真核细胞和原核细胞的核糖体不含膜蛋白，不含磷酸基团B．真核细胞和原核细胞的遗传物质都是DNA，复制时都需要ATP供能C．真核细胞和原核细胞中ATP的合成只与细胞呼吸放能反应有关D．原核基因转录出的mRNA经核孔的蛋白质协助到核糖体上翻译蛋白质2．下图是基因指导蛋白质合成的某个过程示意图，据图分析下列说法错误的是→合成方向A．1是tRNA上的反密码子，可与2上的碱基互补配对B．2是由DNA转录而来的，2中不存在胸腺嘧啶核糖核苷酸C．携带氨基酸的tRNA进入A位后，mRNA沿着核糖体向右移动D．P位的氨基酸与A位氨基酸脱水缩合后转移到A位的tRNA上3．破伤风是破伤风芽孢杆菌在缺氧环境下生长繁殖，产生毒素而引起肌痉挛的一种疾病。

破伤风毒素主要侵袭神经系统中的运动神经元，导致阵发性痉挛等临床特征。

对于事故中伤口很深和出现开放性骨折的人，医务人员要对其注射破伤风人免疫球蛋白针剂。

秘密★启用前 2018 年 4 月绵阳南山中学 2018 年春季高 2018 届理综演练（二）理科综合试题注意事项：1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

答题前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第I 卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3．回答第 II 卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试题和答题卡一并交回。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 Mg 24 Ni 59第Ⅰ卷（选择题共 126 分）本卷共 21 小题，每小题 6 分，共 126 分。

一、选择题：本大题共13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列关于细胞结构和功能的叙述，正确的是A．动物细胞和植物细胞系统的边界分别是细胞膜和细胞壁B．在静息状态下，神经细胞仍进行离子的跨膜运输C．植物细胞的细胞质与细胞核通过胞间连丝实现信息交流D．洋葱根尖细胞分裂过程中周期性变化的结构有染色体和中心体2．下列有关生物的变异和进化的叙述中，正确的是A．用显微镜观察基因突变的位置，最好选择有丝分裂中期B．某褐毛鼠的背部出现一块黑毛，这有可能是生殖细胞突变引起的C．自然选择通过作用于表现型而引起基因频率的定向改变D．某猕猴种群基因频率发生了很大改变，说明新物种已经诞生3．右图表示正常人快速饮入 500mL 某种液体后，其血浆渗透压的变化曲线。

以下分析不合理的是A．若饮入的是清水或 0.9%NaCl 溶液，则体内血浆渗透压变化的曲线依次是 c、bB．当正常人的血浆渗透压出现曲线 a 的变化时，体内抗利尿激素的分泌将会减少C．当饮入 0.9%NaCl 溶液时，细胞外液 Na +的增加远大于细胞内液 Na+的增加D．当血浆渗透压出现曲线 c 的变化时，内环境稳态的调节有激素和神经递质的参与4．下列有关植物激素的相关表述，不正确的是．．．A．采用流水浸泡种子降低脱落酸的含量，有利于种子萌发B．乙烯能促进果实成熟进而产生更多的乙烯，属于反馈调节C．去掉顶芽能抑制侧芽部分生长素的合成，以解除顶端优势D．喷施赤霉素溶液或赤霉菌培养基滤液都能促进水稻生长5．apoB 基因在肠上皮细胞中表达时，由于 mRNA 中某碱基 C 通过脱氨基作用发生了替换，使密码子CAA 变成了终止密码子 UAA，最终合成蛋白质缺少了羧基端的部分氨基酸序列。

南山中学2018级物理二诊模拟测试卷（七）出题：唐家文 审核：王斌1、下列关于振动和波的说法正确的是（ C ）A 、蝙蝠利用发射和接收超声波来确定飞行方向是因为超声波比次声波容易发生衍射B 、根据共振原理，厂房建筑物的固有频率应处在机器振动的频率范围之内C 、当观察者减速靠近波源时，观察者接受到的频率大于波源的频率D 、回复力就是振动的物体所受的合外力2．一定质量的理想气体，如果在某个过程中保持内能不变而放出热量，则在该过程中气体BA ．温度降低B ．压强增大C ．对外做功D ．密度减小 3．夏日中午，河中水面温度高于河底水温，一个气泡从河底升到河面，在此过程中气泡内空气质量不变，则下列说法正确的是（ D ） A 、气泡上升时做匀加速运动B 、气泡上升过程中，浮力对气泡做正功，重力对气泡做负功，所以气泡内气体总内能一定保持不变C 、气泡上升过程中，动能不变D 、气泡上升过程中，对外做功，且要吸热4．在光滑的绝缘水平面上，有一个正方形的abcd ，顶点a 、c 处分别固定一个正点电荷，电荷量相等，如图所示。

若将一个带负电的粒子置于b 点，自由释放，粒子将沿着对角线bd 往复运动。

粒子从b 点运动到d 点的过程中 (D )A ．先作匀加速运动，后作匀减速运动B ．先从高电势到低电势，后从低电势到高电势C ．电势能与机械能之和先增大，后减小D ．电势能先减小，后增大5．A 、B 两物体各自在不同纬度的甲、乙两处受到一竖直向上的外力作用后，在竖直方向上做变加速直线运动。

利用传感器和计算机可以测量快速变化的力与加速度，如图所示是用这种方法获得的物体A 、B 所受的外力F 与加速度a 的关系图线，若物体A 、B 的质量分别为m A 、m B ，甲、乙两处的重力加速度分别为g A 、g B ，两个物体受到的重力分别为G A 、G B ，则（ B ） A ．m A ＞m B ，g A ＞g B ，G A ＞G B B ． m A ＞m B ，g A ＜g B ，G A =G B C ．m A ＞m B ，g A ＜g B ，G A ＞G B D ．m A ＜m B ，g A ＞g B ，G A =G Ba bc d·· FA BOa6．光滑水平面上有两个质量分别是m 、M 的物块A 、B （m <M ）。