表内除法(一)思维导图图片

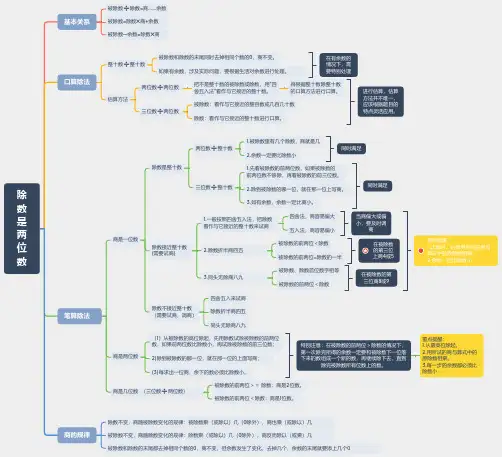
除数是两位数基本关系被除数➗除数=商……余数被除数=除数✖商+余数被除数—余数=除数✖商口算除法整十数➗整十数被除数和除数的末尾同时去掉相同个数的0，商不变。

如果有余数，涉及实际问题，要根据生活对余数进行处理。

估算方法两位数➗两位数把不是整十数的被除数或除数，用“四舍五入法”看作与它接近的整十数。

再根据整十数除整十数的口算方法进行口算。

三位数➗两位数被除数：看作与它接近的整百数或几百几十数除数：看作与它接近的整十数进行口算。

在有余数的情况下，需要特别处理进行估算，估算方法并不唯一，应该根据题目的特点灵活应用。

笔算除法商是一位数除数是整十数两位数➗整十数1.被除数里有几个除数，商就是几2.余数一定要比除数小三位数➗整十数1.先看被除数的前两位数，如果被除数的前两位数不够除，再看被除数的前三位数。

2.除到被除数的哪一位，就在那一位上写商。

3.如有余数，余数一定比商小。

同时满足同时满足除数接近整十数(需要试商)2.除数折半商四五被除数的前两位＜除数被除数的前两位≈除数的一半3.同头无除商八九被除数、除数首位数字相等被除数的前两位＜除数在被除数的第三位商8或9在被除数的第三位上商4或5除数不接近整十数（需要试商、调商）四舍五入来试商重点提醒：1.计算时，必须用所试的商与算式中的原除数相乘。

2.余数一定比除数小商是两位数（1）从被除数的高位除起，先用除数试除被除数的前两位数，如果前两位数比除数小，再试除被除数的前三位数；2)除到被除数的哪一位，就在那一位的上面写商；(3)每求出一位商，余下的数必须比除数小。

商是几位数（三位数➗两位数）被除数的前两位＞＝除数：商是2位数。

被除数的前两位＜除数：商是1位数。

特别注意：在被除数的前两位＞除数的情况下，第一次除完所得的余数一定要和被除数下一位落下来的数组成一个新的数，再继续除下去，直到除完被除数所有位数上的数。

重点提醒：1.从最高位除起。

2.用所试的商与算式中的原除数相乘。

⼩学三年级数学思维导图
⼀、除法
1.整数除法的意义
1.1什么叫除法？
已知两个因数的积和其中⼀个因数，求另⼀个因数叫做除法。

两个因数的积叫做被除数。

其中⼀个因数叫做除数。

所求的另⼀个因数叫商。

例：50÷5=10
50是被除数
5是除数
10是商
1.2除法的意义
除法是乘法的逆运算。

2.有余数除法
2.1有余数除法
如果两个整数相除得不到整数商，那么被除数中最多含有的除数叫做不完全商，所余部分，即被除数减去不完全商与除数的乘积所得的差叫余数。

这种除法叫带余数除法或叫有余数除法。

例如：27÷4=6……3，读作27除以4等于6余3，其中6是不完全商，3是余数。

注意：在有余数的除法⾥，余数⼀定要⽐除数⼩。

2.2有余数除法的各部分的关系
在有余数的除法⾥，被除数等于除数与商相乘的积，再加上余数；除数等于被除数减去余数的差，再除以商。

即：被除数=商×除数＋余数，除数=（被除数－余数）÷商。

3.整数除法的运算法则
3.1表内除法
被除数和除数都是⼀位数，或者被除数是两位数，除数是⼀位数且商是⼀位数的除法，可以⽤乘法⼝诀直接求商。

这样的除法叫表内除法。

一、除法
1.整数除法的意义
1.1什么叫除法？
已知两个因数的积和其中一个因数，求另一个因数叫做除法。

两个因数的积叫做被除数。

其中一个因数叫做除数。

所求的另一个因数叫商。

例：50÷5=10
50是被除数
5是除数
10是商
1.2除法的意义
除法是乘法的逆运算。

2.有余数除法
2.1有余数除法
如果两个整数相除得不到整数商，那么被除数中最多含有的除数叫做不完全商，所余部分，即被除数减去不完全商与除数的乘积所得的差叫余数。

这种除法叫带余数除法或叫有余数除法。

例如：27÷4=6……3，读作27除以4等于6余3，其中6是不完全商，3是余数。

注意：在有余数的除法里，余数一定要比除数小。

2.2有余数除法的各部分的关系
在有余数的除法里，被除数等于除数与商相乘的积，再加上余数；除数等于被除数减去余数的差，再除以商。

即：被除数=商×除数＋余数，除数=（被除数－余数）÷商。

3.整数除法的运算法则
3.1表内除法
被除数和除数都是一位数，或者被除数是两位数，除数是一位数且商是一位数的除法，可以用乘法口诀直接求商。

这样的除法叫表内除法。

除法的初步认识思维导图整理表姓名:职业工种:申请级别:受理机构:填报日期:A4打印/ 修订/ 内容可编辑第1课时有余数除法的认识教材分析生活中,我们在平均分一些物品时常常会出现两种不同的情况,一种是"正好分完”,另一种是“分后还有剩余”,这两种情况是在实践中自然产生的。

"表内除法”主要研究“正好分完”的情况,而“有余数的除法”主要是研究“分后还有剩余”的情况。

"有余数的除法”这部分学习内容是“表内除法”知识的延伸和扩展,也是今后继续学习除法的基础,具有承上启下的作用,必须牢固掌握。

学情分析学生在此之前已经积累了较多的把一些物体进行平均分的活动经验,知道除法运算与平均分的内在联系,也能较熟练地口算表内除法,所以可以在教学新知前,通过看图写算式或看算式进行操作等形式帮助学生回忆有关平均分和除法的知识,便于学生在新旧知识间建立联系。

教学目标知识与技能：初步理解有余数除法和余数的含义，能正确读、写有余数除法的算式.过程与方法：在认识有余数除法的活动中,进一步积累观察、操作、交流等经验;培养学生的分析、抽象、概括能力。

情感态度与价值观：使学生在学习活动中体会数学与生沽的密切联系,增强与他人合作的意识,提高学习数学的兴趣,树立学习数学的信心重点难点重点体会余数产生的过程,初步理解有余数除法的含义.难点有余数除法的含义。

教学准备小棒、圆片、长方形卡片教学步骤一、动手操作,初步感知1.课件出示10÷2.(1)请学生口算,师板书。

师:如果这里的10支铅笔,每人分2支,可以分给几人?(2)学生动手分,并完整地说说10除以2等于5的含义。

【设计意图】对学生已有的知识、经验进行回顾,为学习有余数除法做准备。

2.分组操作,进行记录。

(1)师:如果把这里的10支铅笔,每人分3支,可以分给几个人?学生动手操作,师指名说分小棒的过程、结果。

(2)师:如果每人分3支,最后把10支都分完了吗?剩下的1支为什么不继续分下去呢？比一比,同样是10支铅笔,如果每人分2支或者每人分3支,分的结果有什么不同？(3)师:如果还是这10支铅笔,每人分4支、5支,6支,分得的情况又会怎样呢?同桌分,再将表格填好.出示:【设计意图】要解决这个问题学生要明确两点:一、要把10支铅笔平均分;二,分铅笔时要确定每人分的支数。

数学下册第五单元 混合计算一、混合计算混合运算，先乘除，后加减，有括号的要先算括号里面的。

只有加、减法或只有乘、除法，都要从左到右按顺序计算。

二、解决两步计算的实际问题1、想好先解决什么问题，再解决什么问题。

2、可以画图帮助分析。

3、可以分布计算，也可以列综合算式。

第六单元 有余数的除法一、有余数的除法1、有余数的除法的意义：在平均分一些物体时，有时会有剩余。

2、余数与除数的关系：在有余数的除法中，余数必须比除数小。

最大的余数小于除数1，最小的余数是1。

3、笔算除法的计算方法：（1）先写除号“厂”（2）被除数写在除号里，除数写在除号的左侧。

（3）试商，商写在被除数上面，并要对着被除数的个位。

（4）把商与除数的乘积写在被除数的下面，相同数位要对齐。

（5）用被除数减去商与除数的乘积，如果没有剩余，就表示能除尽。

4、有余数的除法的计算方法可以分四步进行：一商，二乘，三减，四比。

（1）商：即试商，想除数和几相乘最接近被除数且小于被除数，那么商就是几，写在被除数的个位的上面。

（2）乘：把除数和商相乘，将得数写在被除数下面。

（3）减：用被除数减去商与除数的乘积，所得的差写在横线的下面。

（4）比：将余数与除数比一比，余数必须必除数小。

1、把一些物品平均分成几份，如果还有剩余，剩余的部分就是余数。

2、在有余数的除法中，余数一定小于除数3、在有余数的除法中，商×除数+余数＝被除数4、求一个数里面有几个几，用除法计算。

试商时，除数是几，就想几的乘法口诀，积要最接近被除数，而且要小于被除数，这样就可以求出商，再算出余数。

5、用竖式计算有余数的除法一商，想除数和几相乘最接近被除数；二乘，除数和商相乘，把结果写在被除数的下面；三减，用被除数减去商与除数的积；四比，比较一下除数和余数的大小。

6、笔算除法的方法与步骤：（1）先写一个“ ”表示除号，在除号里写被除数，除号外面左侧写除数。

（2）把商写在被除数上面，要和被除数的个位对齐，把除数和商的积写在被除数的下面，注意相同数位要对齐，被除数减去除数和商的积，把差写在横线下面。