下载文档原格式
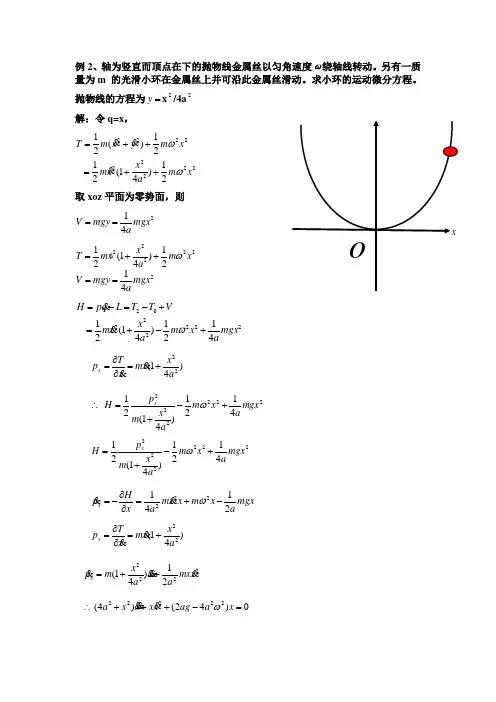
例2、轴为竖直而顶点在下的抛物线金属丝以匀角速度ω绕轴线转动。
另有一质量为m 的光滑小环在金属丝上并可沿此金属丝滑动。
求小环的运动微分方程。
抛物线的方程为=y x 2/4a 2解：令q=x ，取xoz 平面为零势面，则22222222221)41(21 21)(21x m a x x m x m y x m T ωω++=++= 241mgx amgy V ==2222211(1)242x T mxm x a ω=++ 241mgx a mgy V ==222222024121)41(21 mgx a x m a x x m V T T L q p H +-+=+-=-=ω )41(22a x xm x T p x +=∂∂= 2222224121)41(21 m gx a x m a x m p H x +-+=∴ω222222111224(1)4x p H m x mgx x am a ω=-++mgx a x m x x m a x H p x 2141222-+=∂∂-=ω )41(22a x xm x T p x +=∂∂= 222221)41(x mx a xa x m p x ++=0)42()4( 22222=-+++∴x a ag x x xx a ω王月光10070641281. 例5-3 一平面摆，摆锤质量为m 1，摆杆质量为m 3，杆长为l ，视为均质直杆，挂于支点O 处，可在铅直平面内摆动。
另一质量为m 2的小球，光滑地套在摆杆上，它既可以沿摆杆自由滑动，又可以沿半径为R 的固定圆柱形槽内滑动。
不计摩擦，试用哈密顿原理写出系统的运动微分方程。
解：系统具有一个自由度，选ϕ为广义坐标，系统的动能()()22322222131212121ϕϕϕ ⎪⎭⎫ ⎝⎛+++=l m r r m l m T因 ϕcos 2R r =ϕϕ sin 2R r -=所以 22322222161221ϕϕϕ l m R m l m T ++=或 ()()223222222131212121ϕϕ ⎪⎭⎫ ⎝⎛+++=l m y xm l m T 由哈密顿原理d 1=⎰t t t L δ()2cos cos 2cos 612213221223222221ϕϕϕϕϕϕgl m gR m gl m l m R m l m V T L +++++=-= 拉格朗日函数()2cos cos 2cos 3221ϕϕϕgl m gR m gl m V ++-=取O 为重力的零势能位置，系统的势能而ϕϕsin cos 22R x =ϕϕcos cos 22R y =则22322222161221ϕϕϕ l m R m l m T ++=姓名：王月光班级：10070641 学号：1007064128()02sin 2sin 2314231232221=+++⎪⎭⎫ ⎝⎛++ϕϕϕgR m gl m m l m R m l m 由于δϕ为独立变分，故系统的运动微分方程为：则()0d 2sin 2sin 2sin 31410321232221=⎥⎦⎤⎢⎣⎡+++⎪⎭⎫ ⎝⎛++-⎰t t t gl m gR m gl m l m R m l m δϕϕϕϕϕ ()⎰⎰⎰⎰⎰-=-===∴110101011d d d d d d t t t t t t t t t t t t t t t tdt δϕϕδϕϕδϕϕδϕϕδϕϕϕδϕ由于()()010==t t δϕδϕ()0d 2sin 2sin 2sin 26122110321232221=⎥⎦⎤⎢⎣⎡++-⎪⎭⎫ ⎝⎛++⎰t t t gl m gR m gl m l m R m l m δϕϕϕϕϕδϕ 由哈密顿原理d 1=⎰t t t L δ得。
分析力学基础一是非判断题1.不论刚体作何种运动，其惯性力系向一点简化的主矢都等于刚体的质量与其质心加速度的乘积，方向与质心加速度的方向相反。
（√）2. 均质圆柱绕其对称轴作定轴转动，则圆柱惯性力系对于空间中平行于转轴的任意一轴的力矩之和，都是同一值。
（√）3. 因为实位移和虚位移都是约束允许的，所以实际的微小位移必定是诸虚位移中的一个。
（×）4. 虚位移原理只适用于具有理想约束的系统。
（×）5. 凡几何约束都是完整约束，完整约束未必是几何约束。
（√）二选择题1.下列约束中，非理想约束的是（B ）。
A 纯滚动，有摩擦力但无滚动摩阻。
B 有摩擦的铰链。
C 摩擦传动中两个刚性摩擦轮的接触处，两轮间不打滑，无滚动摩阻。
D 连接两个质点的不可伸长的柔索。
2. 如图所示四种情况，惯性力系的简化只有（ C ）图正确。
3. 均质细杆AB质量为m，长为L，置于水平位置，如图所示。
若在绳BC突然剪断时角加速度为α，则杆上各点惯性力的合力大小为（12mLα），方向为（垂直向上），作用点的位置在杆的（左端A ）处4. 四根等长等重的均质直杆用铰链连接起来，再把两端用铰链固定在同一水平线上，如图所示，平衡时图示两个角度α和β的关系是（ B ）。
第二(3)题图第二(4)题图A ．tan 3tan βα=； B. tan 3tan αβ= C. tan 2tan βα=; D. tan 2tan αβ=5. 图示系统中，O 处为轮轴，绳与滑轮间无相对滑动，则物块A 与物块B 的虚位移大小的比值为（ B ）。
A ．6；B ．5；C ．4；D ．3.三 填空题1. 图示平面系统，圆环在水平面上作纯滚动，圆环内放置的直杆AB 可在圆环内自由运动，A ，B 两点始终与圆环保持接触，则该系统的自由度数为（ 2 ）。
2. 轮轴质心位于O 处，对轴O 的转动惯量为O J 。
在轮轴上系有两个质量各为1m 和2m 的物体，已知此轮轴顺时针转向转动，角加速度为α，则轴承O 处的动反力Ox F =( 0 ), Oy F =（ 12()m R m r α-）。
图2-1-7图2-2-2高一物理力学受力分析1如图2-1-7所示，甲、乙球通过弹簧连接后用绳悬挂于天花板，丙、丁球通过细绳连接后也用绳悬挂天花板．若都在A 处剪断细绳，在剪断瞬间，关于球的受力情况，下面说法中正确的是（ ）A ．甲球只受重力作用B ．乙球只受重力作用C ．丙球受重力和绳的拉力作用D ．丁球只受重力作用分析：当在A 处剪断时两球看作一个整体，整体加速度为g ，此时弹簧中的力不变，对A B 球都会有力的作用故A B 错，绳在松弛状态不能提供力，假设绳中有拉力，则丁的加速度会大于g 而丙的加速度会小于g ，则两球会相互靠近，绳则松弛，假设不成立，故绳中无拉力2．如图2-2-8所示，物体a 、b 和c 叠放在水平桌面上，水平力F b =5N 、F c =10N 分别作用于物体b 、c 上，a 、b 和c 仍保持静止．以F 1、F 2、F 3分别表示a 与b 、b 与c 、cA ．F 1=5N ，F 2=0，F 3=5NB ．F 1=5N ，F 2=5N ，F3=0 C ．F 1=0，F 2=5N ，F 3=5ND ．F 1=0，F 2=10N ，F 3=5N 分析：（分析方法从简单到复杂）因为a 、b 、c 均保持静止，故加速度，合外力都为0。
先分析a 只受b 对a 的支持力，以及重力故F1=0，再分析b ，b 受到重力、a 对b 的压力、c 对b 的支持力、Fb 、以及c 对b 的摩擦力，c 对b 的摩擦力为水平方向，故需水平方向的力来平衡，故F2=Fb=5，方向向右。
同理在对c 分析3如图2-2-1所示，A 、B 两物体叠放在水平面上，水平力F 作用在A 上，使两者一起向右作匀速直线运动，下列判断正确的是（ ）A ．A 、B 间无摩擦力 B ．A 对B 的静摩擦力大小为F ，方向向右C ．B 对地面的动摩擦力的大小为F ，方向向右D ．B 受到了向右的静摩擦力和向左的滑动摩擦力分析：两者一起向右作匀速直线运动，则加速度都为0，处于平衡状态。
圆环套圆柱的分析力学习题
解：，这个物体受到重力和支持力，即为：力，设物体与底面接触点为 A，它受到沿水平方向的重力和竖直方向的支持力的作用，则可列出力的示意图：由于物体所受合外力为零，在一定限度内只有重力做功。
因此，在上述过程中，合外力对物体只有两种效果：使物体形状改变或者保持不变。
根据第二类永动机实验的结论知道，在无摩擦、无阻力的情况下，如果两个圆环之间存在空气隔层，则圆环套在圆柱上会发生“自锁”现象。
当圆环之间紧密贴合时，将圆环压缩后，若再抽去部分空气（即减小了圆环与圆柱之间的距离），则这两个圆环又会恢复原来的接触状态，并且认为合成总的圆环没有任何位移。
由于圆环绕着圆柱转动，所以圆环也必然随着圆柱运动而运动，从而构成了一种复杂的机械系统。
显然，“不自觉地服从了相对性原理的结论”是这种“力学奇观”得以产生的前提条件。
尽管人们对此还不能完全确信，但科学家经过进一步研究已证明：不管你愿不愿意承认，任何现代化的交通工具——包括火车、汽车、飞机等都逃脱不了某些最基本的力学规律，尤其是牛顿三大定律的约束。
至少我们可以说，这些被视为神秘莫测的高级物质——飞船、卫星及航天飞机等的运行原理，早就超越了狭义的力学范畴。
- 1 -。
《理论力学》第五章分析力学一、单选题（共6题）1、广义坐标必须是:()A、笛卡儿坐标B、独立的位置变量C、角坐标或弧坐标;D、任何位置变量正确答案：B2、关于虚位移下列表述中不正确的是:()A、与约束有关;B、与时间无关;C、与主动力有关;D、一般不唯一正确答案：C解析：虚位移不是真实发生的位移,而是想象中可能发生的位移,它只取决于质点在此时刻的位置和加在它上面的约束,而不是由于时间的改变所引起的。
3、保守系的拉格朗日函数等于系统的:()A、总动能加总势能;B、总动能减总势能;C、总势能减总动能;D、广义速度的二次式正确答案：B解析：L=T-V。
4、分析力学中哈密顿正则变量为:()A、广义速度和广义坐标;B、广义速度和广义动量;C、广义动量和广义坐标;D、广义能量和广义动量.正确答案：C5、关于分析力学中的概念,找出错误的说法()A、拉格朗日方程是S个二阶常微分方程组成的方程组;B、哈密顿正则方程是2S个一阶常微分方程组成的方程组;C、拉格朗日函数和哈密顿函数的变量不同;D、拉格朗日方程和哈密顿正则方程是分析力学中两个基本的方程,不能相互推演。
正确答案：D解析：A、拉格朗日方程为,是由S个二阶常微分方程组成的方程组;B、哈密顿正则方程为,是由2S个一阶常微分方程组成的方程组;C、;D拉格朗日方程和哈密顿正则方程是分析力学中两个基本的方程，可以互相推演。
6、一质点质量为m,速度v,势能为Ep,则其拉格朗日函数为:____正确答案：B解析：L=T-V.二、填空题（共7题）1、一个不受任何约束的系统,由n个质点组成,该系统的独立坐标个数为____个;若该系统受k个完整约束,m个非完整约束,则该系统的自由度数目变为____个;独立坐标(广义坐标)个数变为____个。
正确答案：第1空:3n第2空:3n-k-m第3空:3n-k2、虚位移是____允许的所有位移,与时间____。
正确答案：第1空:稳定约束第2空:无关3、理想完整系统是指只受____、____的系统。
湖北第二师范学院2010学年春季学期期末考试《分析力学》2、 一圆盘质量为m ，半径为R ，盘面在竖直平面内绕盘边缘过O 点与盘面垂直的轴以匀角速 转动，如图(1)所示。
则圆盘的动量是 _________________ ，动量矩是____________________ ，动能是 _________________3、 质量为m i 及m 2的两自由质点互相以力吸引，引力与其质量成正比，与距离平方成反比， 比例系数为k o 开始时，两质点皆处于静止状态，距离为a 。
则当两质点距离为a/2时，质点m 〔 的速度是 ___________________ ，质点 m 2的速度是 ______________ o4、 某一时刻，冈体上本体极迹和空间极迹的交点叫做 ____________ ，该点相对于地面而言， 其速度为 ______________ o5、 科里奥利加速度存在于 __________ 考系中；惯性离心力存在于 ____________ 考系中。
6、 在曲面上自由运动的一质点的自由度数目为 _____________ 在曲线上自由运动的一质点 的自由度数目为 _____________ o7、 质量为m 的自由质点在重力场中运动时，在直角坐标系中该质点的拉格朗日函数表达式 为由此可得质点的运动特征是2、一端固定于天花板上的细绳缠绕在一个半径为 r 0.2m ，质量为m 3kg 的均质圆 盘上，如右图（4）所示。
求圆盘中心运动的加速度a c ，圆盘的角加速度 及绳子的张力T 。
（15 分）图（4）3、试用拉格朗日方程和哈密顿方程导出由长度为I 的不可伸长的细线与质量为 m 的摆球所得分 评卷人二、判断题（对者打"，错者打X ，每小题 2分，共10 分） 1、质点在有心力场中运动时，其轨迹必为一平面曲线。
（ ）2、 由于质点组的内力成对出现，所以内力的功之和恒等于零。
3、 刚体作平面平行运动时， 其动能为平动动能与转动动能的和。
图2-1-71，如图2-1-7所示，甲、乙球通过弹簧连接后用绳悬挂于天花板，丙、丁球通过细绳连接后也用绳悬挂天花板．若都在A 处剪断细绳，在剪断瞬间，关于球的受力情况，下 面说法中正确的是（ ） A ．甲球只受重力作用 B ．乙球只受重力作用C ．丙球受重力和绳的拉力作用【解析】剪断A 处绳的瞬间，因为弹簧的形变较大，所以在极短的时间内，形变不发生变化，弹力仍和剪断前相同，甲球受重力和向上的弹力作用，其合力为零，乙球受重力和向下的弹力作用；而由于丙、丁的细绳的形变很小，形变发生变化，弹力和剪断前不同，丙、丁只受重力作用．故选项D 正确．2．如图2-1-19所示，滑轮本身的质量可忽略不计，滑轮轴O 安装在一根轻木杆B 上，一根轻绳AC 绕过滑轮，绳与滑轮间的摩擦不计，A 端固定在墙上，且绳保持水平，C 端下面挂一个重物，BO 与竖直方向夹角θ=45°，系统保持平衡.若保持滑轮的位置不变，改变θ的大小，则滑轮受到木杆的弹力大小变化的情况是（D ） A ．只有角θ变小，弹力才变小 B ．只有角θ变大，弹力才变大C ．不论角θ变大或变小，弹力都变大θ变大或变小，弹力都不变【解析】绳A 与绳C 的拉力大小与方向均不变，所以其合力不变，对滑轮而言，杆的作用力必与两绳拉力的合力平衡，所以杆的弹力大小与方向均不变．解决这类问题关键是区别杆、绳对物体的作用力，绳对物体的作用力一定沿绳，但杆对物体作用力不一定沿杆．3如图2-2-1所示，A 、B 两物体叠放在水平面上，水平力F 作用在A 上，使两者一起向右作匀速直线运动，下列判断正确的是（ ） A ．A 、B 间无摩擦力B ．A 对B 的静摩擦力大小为F ，方向向右C ．B 对地面的动摩擦力的大小为F ，方向向右D ．B 受到了向右的静摩擦力和向左的滑动摩擦力【解析】A 做匀速运动，故A 的合力为零．由于它受到一个向右的拉力，因此它一定还要受到一个向左的水平力与力F 平衡，所以B 对A 一个水平向左的静摩擦力为F 平衡，由牛顿第三定律可知， A 一定要对B 施加一个向右的静摩擦力；B 做匀速直线运动，它在水平方向上一定要受到一个向左的力与A 对B 的静摩擦力平衡；B 是在水平面上运动，显然地面对B 有一个向左的滑动摩擦力，那么B 对地面施加一个向右的滑动摩擦力．因此选项BCD 正确．4如图2-2-3所示，物体A 、B 的质量m A =m B =6kg ，A 和B 、B 和水平面间的动摩擦因数都等于0.3，且最大静摩擦力等于滑动摩擦力，水平力F =30N ．那么，B 对A 的摩擦力和水平桌面对B 的摩擦力各为多大?【解析】假设A 相对于B 、B 相对于桌面均不发生滑动，则绳对A 、B 的拉力大小均为2302==F F T N=15N ．A 、B 间的最大静摩擦力F Am =μF NA =μm A g =0.3×6×9.8N=17.64N ＞F T ，B 与桌面间的最大静摩擦力F Bm =μF NB=μ（m A + m B ）g =0.3×（6+6）×9.8 N=35.28N ＞F ，可见以上假设成立．对A 应用二力平衡条件，可得B 对A 的摩擦力F BA = F T =15N ．对A 、B 和滑轮整体应用二力平衡条件，可得桌面对B 的摩擦力 F 桌B =F =30N ．5．如图，水平面上有一重为40N 的物体，受到F1＝12N 和F2＝6N 的水平力作用而保持静止。
第15章虚位移原理解题的一般步骤及应注意的问题１．解题的一般步骤（１）根据题意，分清所分析的问题是属于哪一类问题①求平衡条件；②求约束反力；③求桁架内力。
（2）分析约束的性质, 画主动力的受力图.①系统以外的物体对它的作用力；②非理想约束的约束反力；③因解除约束而“转化”为主动力的约束反力或内力。
（3）确定系统的自由度，应包括因解除约束而增加的自由度。
选择合适的坐标做广义坐标。
（4）给出系统的虚位移，采用如下方法计算主动力作用点的虚位移与广义坐标虚位移间的关系：①几何法：运用运动学中分析速度的方法，进行计算。
②分析法：先选一静坐标系，用广义坐标写出主动力（力矩）作用点的坐标分析表达式，然后再对广义坐标取变分，进行计算。
（5）建立虚功方程，计算各主动力在给定虚位移中的虚功，建立虚功方程，确定平衡条件，求出待求的参量。
2.应注意的问题1应用虚位移原理，一般都是以整个系统为研究对象，不宜选取分离体。
2计算弹性力在虚位移中的虚功时，弹性力的大小与虚位移的大小无关。
3在计算转动刚体（或平面运动刚体）上的主动力的虚功时，如果把主动力的虚功转化为主动力对转动轴（或瞬时转动轴）之力矩的虚功，可能简便些。
三、典型例题分析例1 图示曲柄连杆机构, 在曲柄OA上作用一力偶矩为M的力偶, 欲使机构在图示位置保持平衡, 试求加于滑块B上的水平力P应为多大? 已知OA=a, AB=b, 在图示位置AB与水平线的夹角α=30º解: 这是属于求主动力的平衡条件的问题。
作用于系统和主动力有Ｐ和Ｍ。
系统受完整约束，有一个自由度，当机构有虚位移时，ＯＡ作定轴转动，曲柄ＡＢ作平面运动，滑块Ｂ作平动。
令ＯＡ杆的虚位移为δϕ，则Ａ点虚位移为δr A, B点虚位移为δr B, AB杆的虚位移为绕瞬心C的微小转角δψ, 机构的虚位移如图。
根据虚位移原理得：Ｐδr B－Ｍδϕ＝０（１）3r , A B δϕδδδψδδψδϕδa AC BC r BC r AC a r B A ==∴===代入（１）式得：03=-δϕδϕM a PaM P 30=∴≠δϕ 15-1 图示曲柄式压缩机的销钉B 上作用有水平力F ，此力位于平面ABC 内。
作用线平分ABC ∠。
设AB = BC ，θ2=∠ABC ，各处摩擦及杆重不计，求对物体的压缩力。
解：令B 有虚位移AB B ⊥r δ，而C 有铅直向上的虚位移C r δ，如图（a ）。
将B r δ及C r δ向BC 方向投影，为简单起见，以B r δ表示B r δ的绝对值B r δ，以C r δ表示C r δ，则有)902cos(δ)90cos(δ︒-=-︒θθB C r r即 θcos 21δδ=C B r r （1） 由虚位移原理得 0δsin δN =-C B r F r F θθsin δδN F F r r C B =（2）将式（1）代入（2）得 θtan 2N FF =15-3 挖土机挖掘部分示意如图。
支臂DEF 不动，A 、B 、D 、E 、F 为铰链，液压油缸AD 伸缩时可通过连杆AB 使挖斗BFC 绕F 转动，EA = FB = a 。
当︒==3021θθ时杆DF AE ⊥，此时油缸推力为F 。
不计构件重量，求此时挖斗可克服的最大阻力矩M 。
解：由虚功原理： 0δδcos 1=-⋅ϕθM r F A （1） 式中ar Bδδ=ϕ （2）A 、B 的虚位移向AB 投影 22sin δcos δθθB A r r =2tan δδθB A r r =（3）式（2），（3）代入（1）得 0δδtan cos 21=⋅-⋅⋅ar M r F BB θθFa M Fa M 21,sin ,30221==︒==θθθ 15-5 在图示机构中，当曲柄OC 绕O 轴摆动时，滑块A 沿曲柄滑动，从而带动杆AB 在铅直导槽K 内移动。
已知：OC = a ，OK = l ，在点C 处垂直于曲柄作用一力F 1；而在点B 沿BA 作用一力F 2。
求机构平衡时F 2与F 1的关系。
解：用解析法解，选取ϕ为广义坐标，则滑块A 的约束方程ϕtan l y A =ϕϕδsec δ2l y A = （1）由虚位称原理0δδ)(21=+-A y F a F ϕ （2）把式（1）代入（2）得 0δsec δ221=+-ϕϕϕl F a F因 0δ≠ϕ，于是有 0sec 221=+-ϕl F a F故 ϕ221cos a l F F=15-7 图示滑套D 套在光滑直杆AB 上，并带动杆CD 在铅直滑道上滑动，已知︒=0θ时弹簧为原长，弹簧刚性系数为5 kN/m 。
求在任意位置平衡时，应加多大的力偶矩M ？ 解：解除弹簧约束，代之以弹性力F 及F '。
已知0=θ时弹簧原长为0.3 m ，在任意θ角时，弹簧)cos 3.06.0(θ-=-=AD AB DB ，此时弹簧的缩短量为)3.0cos 3.0(3.0-=-θDB 。
故弹性力 F F '=)3.0cos 3.0(-=θk 取x 轴沿AB 杆，设D 点沿杆的坐标为x D ，而选取θ为广义坐标，则滑块D 的约束方程为θcos 3.0=D x ，θθθδcos sin 3.0δ2=D x 另外有 x B = 常量，0δ=B x由虚位移原理0δδ)(=+-θM x F D 把F 及D x δ的表达式代入上式得0δδcos sin 3.0)3.0cos 3.0(2=+⋅--θθθθθM kθθθ2cos sin 3.0)1cos 1(3.0⋅-⋅=k M 把k = 5000 N/m 代入求得 m N cos )cos 1(sin 4503⋅-=θθθM15-9 在图示机构中，曲柄AB 和连杆BC 为均质杆，具有相同的长度和重量W 1。
滑块C 的重量为W 2，可沿倾角为θ的导轨AD 滑动。
设约束都是理想的，求系统在铅垂面内的平衡位置。
解：取ϕ为广义坐标，另作坐标系Axy ，设AB = BC = l 因 )sin(21ϕθ+=lyθϕθθϕθϕθϕθsin cos 2sin )(2sin cos 2)sin(2sin 2l AC y ll l AC y C ==-+=-+= 对坐标的变分：ϕθϕϕθϕθϕϕϕθδsin sin 2δδ)cos(2sin sin 2δδ)cos(2δ21l -y l l y ly C =⎥⎦⎤⎢⎣⎡-+-=+=由虚位移原理0δδδ22111=++C y W y W y W 即 0δsin sin 2)cos(2sin sin 2)cos(221=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡-+-+ϕθϕθϕθϕϕθl W l l l W 因0δ≠ϕ，故有0sin sin 2)cos(2sin sin 2)cos(221=-⎥⎦⎤⎢⎣⎡-+-+θϕθϕθϕϕθl W l l l W即1cot cot 21sin sin 2sin sin 2cos cos 12-=-=ϕθϕθϕθϕθW W 故 θϕcot )(2tan 211W W W +=15-11 图示均质杆AB 长为2l ，一端靠在光滑的铅直墙壁上，另一端放在固定光滑曲面DE 上。
欲使细杆能静止在铅直平面的任意位置，问曲面的曲线DE 的形式应是怎样的？ 解：作坐标系Dxy ，由于杆AB 只受主动力W 作用，根据虚位移原理 0δ=C y W 0≠W 0δ=C y ，故y C = 常量杆在铅直位置时y C 0 = l ， y C = l 杆在任意位置时y C = y A + l cos ϕ， 即 ϕcos l y l A +=ϕϕsin 2)cos 1(l x l y A A =-=消去ϕ得DE 曲线方程1)(42222=-+l y l l x A A 由方程知 ，DE 曲线为中心在（0，l ）长短半轴分别为2l 和l 的椭圆的一部分。
如坐标系Dxy 向上平移l 距离，则DE 曲线方程与书中答案一致。
15-13 半径为R 的滚子放在粗糙水平面上，连杆AB 的两端分别与轮缘上的A 点和滑块B 铰接。
现在滚子上施加矩为M 的力偶，在滑块上施加力F ，使系统于图示位置处平衡。
设力F 为已知，忽略滚动摩阻和各构件的重量，不计滑块和各铰链处的摩擦，试求力偶矩M 以及滚子与地面间的摩擦力F s 。
解：作功力M ，F ，虚功方程为：0δ2δ=-B As F Rs MA s δ，B s δ向AB 投影： ︒=45cos δδB A s s0δ)2/(δ22=-⋅B B s F R s M M = 2RF 0=∑x F， F s = F15-15 试用虚位移原理求图示桁架中杆3的内力。
解：将BD 杆解除代之以力F 及F '。
令C 点有虚位移C r δ，则B 点必有虚位移B r δ D 点必有虚位移D r δ，如图（a ）。
由虚位移原理0δ90cos δδP =-︒'+D D B r F r F r F 即PδδF F r r B D = （1）由图（a ）可见，ACD 框的转轴在A 点， CB 杆的瞬心在E 点 故 AC ADr r C D =δδ 及EBECr r B C =δδ 所以 1636366δδδδδδ2222=+⋅+=⋅=B C C D B D r r r r r r （2）由式（1）、（2）得 P F F F ='=（拉力）例15-4 在水平面内运动的行星齿轮机构如图15-4所示。
均质系杆OA 的质量为m 1，它可绕端点O 转动，另一端装有质量为m 2，半径为r 的均质小齿轮，小齿轮沿半为R 的固定大齿轮纯滚动。
当系杆受力偶M 的作用时，试求系杆的角加速度。
图15-4【解】 机构具有一个自由度，选系杆的转角φ为广义坐标。
设系杆对O 轴的转动惯量为J O ，小齿轮对其质心A 的转动惯量为J A ，小齿轮的绝对角速度为，则A 点的速度为小齿轮的角速度系统的动能等于系杆的动能和小齿轮的动能之和，即与广义坐标对应的广义力将上两式代入拉氏方程例题2 三铰拱如图所示,求支座B 的约束反力。
解: (1)求支座B 的铅垂反力, 解除支座B 的铅垂约束,代之约束反力Y B ,如图所示, 该系统有一个自由度: AC 绕A 定轴转动, BC 做平面运动, 瞬心为A, 画虚位移图如图。
利用虚位移图，δr C =(AC )δθ1 =(AC )δθ2δθ1 = δθ2 = δθ 利用虚位移图计算虚功 δW (m ) = m δθ1δW (P ) = aP δθ2由虚位移原理，m δθ+ aP δθ -2aY B δθ = 0A22P a m Y B +=(2)求支座B 的水平反力, 解除支座B 的水平约束, 代之约束反力X B ,如图所示, 该系统有一个自由度: AC 绕A 定轴转动,BC 做平面运动, 瞬心为I , 画虚位移图如图。
