分析力学第一章作业答案

分析力学参考答案分析力学参考答案引言：分析力学是物理学的一个重要分支，研究物体在力的作用下的运动规律。

在学习分析力学的过程中，参考答案是一个非常重要的工具，可以帮助学生巩固知识，理解问题的解决方法。

本文将分析力学的一些典型问题，并给出参考答案，帮助读者更好地掌握分析力学的基本原理和解题技巧。

一、牛顿第二定律问题牛顿第二定律是分析力学的基础，描述了物体在力的作用下的加速度。

以下是一个典型的牛顿第二定律问题：问题：一个质量为m的物体在水平面上受到一个恒定的力F作用，求物体的加速度和受力大小的关系。

解答：根据牛顿第二定律的公式F=ma，我们可以得到物体的加速度a等于受力F除以物体的质量m，即a=F/m。

因此，物体的加速度与受力大小成反比。

二、动量守恒问题动量守恒是分析力学中的一个重要原理，描述了系统在没有外力作用下动量的守恒。

以下是一个典型的动量守恒问题：问题：两个质量分别为m1和m2的物体在水平面上碰撞，碰撞前物体1的速度为v1，物体2的速度为v2，碰撞后物体1的速度为v'1，物体2的速度为v'2，求碰撞前后两个物体的动量是否守恒。

解答：根据动量守恒定律，系统在没有外力作用下，动量守恒。

即m1v1 +m2v2 = m1v'1 + m2v'2。

因此，两个物体的动量在碰撞前后保持不变，动量守恒。

三、角动量问题角动量是分析力学中的一个重要概念，描述了物体绕某一点旋转的特性。

以下是一个典型的角动量问题：问题：一个质量为m的物体绕固定点O以角速度ω旋转，求物体的角动量L 与角速度ω的关系。

解答：根据角动量的定义L=Iω，其中I为物体对固定点O的转动惯量。

对于一个质量为m的物体，其转动惯量I等于mr^2，其中r为物体到固定点O的距离。

因此，物体的角动量L与角速度ω成正比，L=mr^2ω。

结论：通过以上的分析力学问题及其参考答案，我们可以看出分析力学的基本原理和解题技巧。

牛顿第二定律描述了物体在力的作用下的加速度，动量守恒原理描述了系统在没有外力作用下动量的守恒，角动量则描述了物体绕某一点旋转的特性。

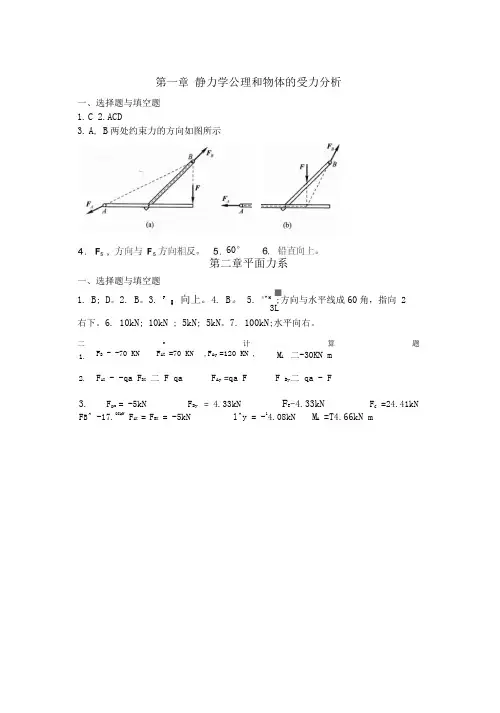
第一章静力学公理和物体的受力分析一、选择题与填空题1.C2.ACD3.A, B两处约束力的方向如图所示60°第二章平面力系一、选择题与填空题■1. B; D。

2. B。

3. F；向上。

4. B。

5. 4^M;方向与水平线成60角，指向 23L右下。

6. 10kN; 10kN ; 5kN; 5kN。

7. 100kN;水平向右。

二•计算题1. F B - -70 KN F AX =70 KN ,F Ay =120 KN , M A二-30KN m2. F AX - -qa F BX二 F qa F Ay =qa F F By 二 qa - F3. F= -5kN F Dy = 4.33kN F E-4.33kN F C =24.41kND xF B^ -17.08kN F AX=F BX = -5kN l^y = -14.08kN M A=T4.66kN mF AX =10N FAy =20N M A =15N mF CD =14.1N6F Ax=2.5kN F Ay=—2.16kN M A=」kN ，m F c =20.33kN7 F B=40kNF AX = —10kNFA ^-20kN M -50kN m F cx = 40kNF ey = 0F HX =300N F Hy =100N第三章空间力系少2(-8. F A ^ = -100N F Ay 二-300N F Ex 二-300N F Ey =100N F °y 二 200N整=一一A > X Y m 一：J E £c X一、选择题与填空题f—- - Fa 6 Fa 1.B。

2.B。

3. M x(F)=O ; M y(F) —H2 44.F x=-40.2N; F y=30-2N; M z=240.2 N m。

5.F z= F sin :；F y= F cos ：cos :;M x(F)二 F(ccos'cos ： bsin )。

理论力学2章作业题解1-1 支座受力F ，已知F ＝10kN ，方向如图所示。

求力F 沿x 、y 轴及沿x ′、y ′轴分解的结果，并求力F 在各轴上的投影。

解答 分力的大小需按平行四边形法则进行计算。

F 在x ，y 轴上的分力大小为：kN F F x 66.830cos ||0==r ，kN F F y 0.530sin ||0==r 。

F 在x ¢，y ¢轴上的分力大小为：kN F F x 0.10||==¢r ，kN F F y 17.515sin 2||0=´=¢r 。

F 在x ，y 轴上的投影大小为：kN F F x 66.830cos 0==，kN F F y 0.530sin 0==。

F 在x ¢，y ¢轴上的投影大小为：kN F F x 66.830cos 0==¢，kN F F y 59.275cos 0-=-=¢。

1-3计算图中F 1、F 2、F 3三个力分别在x 、y 、z 轴上的投影。

已知F 1＝2kN ，F 2＝1kN ，F 3＝3kN 。

解答 0.0,6.18.0,2.16.011111==´=-=´-=z y x F kN F F kN F F .kN F F kN F F kN F F z y x 707.0,566.08.0,424.06.0222222222222=´==´´==´´=kN F kN F kN F z y x 0.3,0.0,0.0333===1-5 力F 沿正六面体的对顶线AB 作用，F ＝100N 。

求F 在ON 上的投影。

解答 计算ON 方向的单位矢量n 。

k j kj n 447.0894.020040020040022+=++=力F 的解析表达式为：k j i k j i F 470.62470.62852.46 400400300)400400300(100222++-=++++-= 力F 在ON 轴的投影为N F ON 78.83447.047.62894.047.62=´+´=×=n F题1-1 附图题1-3 附图 题1-5 附图1-8试求附图所示绳子张力F Ｔ对A 点及对B 点的矩。

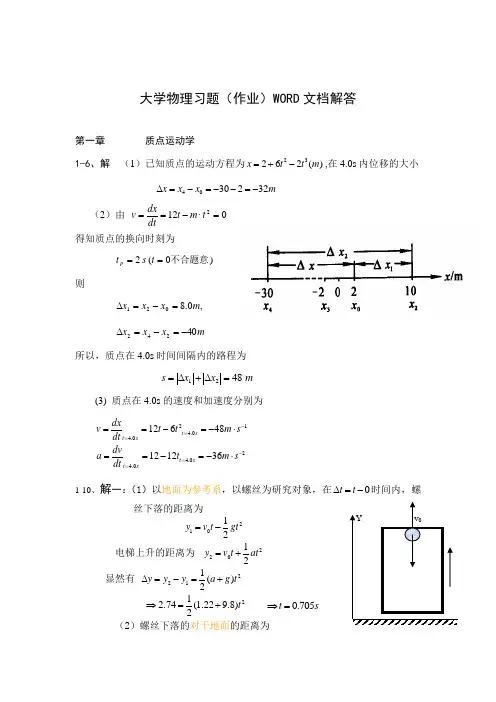
大学物理习题（作业）WORD 文档解答第一章 质点运动学1-6、解 （1）已知质点的运动方程为23262()x t t m =+-,在4.0s 内位移的大小 4030232x x x m ∆=-=--=- （2）由 0·122=-==t m t dtdxv 得知质点的换向时刻为)0(2不合题意==t s t p则,0.8021m x x x =-=∆ m x x x 40242-=-=∆所以，质点在4.0s 时间间隔内的路程为 m x x s 4821=∆+∆=(3) 质点在4.0s 的速度和加速度分别为214.04.024.04.012648121236t s t st s t sdxv t t m s dt dv a t m s dt -==-====-=-⋅==-=-⋅1-10、解一：（1）以地面为参考系，以螺丝为研究对象，在0t t ∆=-时间内，螺丝下落的距离为21012y v t gt =-电梯上升的距离为22012y v t at =+显然有 2211()2y y y a g t ∆=-=+212.74(1.229.8)2t ⇒=+ 0.705t s ⇒=（2）螺丝下落的对于地面的距离为2210112.440.7059.8(0.705)0.71622y v t gt m =-=⨯-⨯⨯=- 解二：（1）以电梯为参考系，螺丝对于电梯的加速度为()a g j -+,而初速度为零，因此有21()2y a g t ∆=+ 212.74(1.229.8)0.7052t t s ⇒=+⇒= （2）螺丝下落的对于地面的距离为2210112.440.7059.8(0.705)0.71622y v t gt m =-=⨯-⨯⨯=-1-11 一质点P 沿半径m R 00.3=的圆周作匀速速率运动，运动一周所需时间为20.0s ，设t=0时，质点位于O 点，按图1-5(a)中所示Oxy 坐标系，求（1）质点P 在任意时刻的位矢；（2）5 s 时的速度和加速度。

第一章 思考题1.1平均速度与瞬时速度有何不同？1.2 在极坐标系中，r v r =，θθ r v =.为什么2θ r r a r-=而非r ？为什么θθ r r a 20+=而非θθ r r +？你能说出r a 中的2θ r -和θa 中另一个θ r 出现的原因和它们的物理意义吗？1.3 在内禀方程中，n a 是怎样产生的？为什么在空间曲线中它总沿着主法线方向？当质点沿空间运动时，副法线方向的加速度b a 等于零，而作用力在副法线方向的分量b F 一般不等于零，这是不是违背了牛顿运动定律呢？1.4 在怎样的运动中只有τa 而无n a ？在怎样的运动中又只有n a 而无τa ？在怎样的运动中既有n a 而无τa ？1.5dt r d 与dt dr 有无不同？dt v d与dtdv 有无不同？试就直线运动与曲线运动分别加以讨论. 1.6人以速度v 向篮球网前进，则当其投篮时应用什么角度投出？跟静止时投篮有何不同？1.7雨点以匀速度v 落下，在一有加速度a 的火车中看，它走什么路经？1.8某人以一定的功率划船，逆流而上.当船经过一桥时，船上的渔竿不慎落入河中.两分钟后，此人才发现，立即返棹追赶.追到渔竿之处是在桥的下游600米的地方，问河水的流速是多大？1.9物体运动的速度是否总是和所受的外力的方向一致？为什么？1.10在那些条件下，物体可以作直线运动？如果初速度的方向和力的方向一致，则物体是沿力的方向还是沿初速度的方向运动？试用一具体实例加以说明.1.11质点仅因重力作用而沿光滑静止曲线下滑，达到任一点时的速度只和什么有关？为什么是这样？假如不是光滑的将如何？1.12为什么被约束在一光滑静止的曲线上运动时，约束力不作功？我们利用动能定理或能量积分，能否求出约束力？如不能，应当怎样去求？1.13质点的质量是1千克，它运动时的速度是k j i v 323++=，式中i 、j 、k 是沿x 、y 、z 轴上的单位矢量。

理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图，各接触面均为光滑面。

1-2 画出下列指定物体的受力图，各接触面均为光滑，未画重力的物体的重量均不计。

1-3 画出下列各物体以及整体受力图，除注明者外，各物体自重不计，所有接触处均为光滑。

(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在铰车D 上，如图所示。

转动铰车，物体便能升起，设滑轮的大小及滑轮转轴处的摩擦忽略不计，A、B、C三处均为铰链连接。

当物体处于平衡状态时，试求拉杆AB和支杆CB所受的力。

2-2 用一组绳悬挂重P=1kN的物体，求各绳的拉力。

2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN，P2=800kN及制动力T=193kN，桥墩自重W=5280kN，风力Q=140kN。

各力作用线位置如图所示，求将这些力向基底截面中心O简化的结果，如能简化为一合力，试求出合力作用线的位置。

2-4 水平梁的支承和载荷如图所示，试求出图中A、B处的约束反力。

2-5 在图示结构计算简图中，已知q=15kN/m，求A、B、C处的约束力。

2-6 图示平面结构，自重不计，由AB、BD、DFE三杆铰接组成，已知：P=50kN，M=40kN·m，q=20kN/m，L=2m，试求固定端A的反力。

图2-6 图2-72-7 求图示多跨静定梁的支座反力。

2-8 图示结构中各杆自重不计，D、E处为铰链，B、C为链杆约束，A为固定端，已知：q G=1kN/m，q=1kN/m，M=2kN·m，L1=3m，L2=2m，试求A、B、C 处约束反力。

图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成，O、B处为铰链，A、E是固定铰支座，尺寸如图，已知：r=20cm，在滑轮上吊有重Q=1000N的物体，杆及轮重均不计，试求支座A和E以及AO杆上的O处约束反力。

大学物理答案-第一章第一章力学引论本章主要阐述了力学的研究内容（即物体的机械运动），以及矢量分析和量纲分析的方法。

习题1-1 什么叫质点？太阳、地球是质点吗？分子、原子是质点吗？试举例说明。

分析：本题说明参考系选择的重要性。

对于相同的物体，如果参考系的选择不同，结果将完全不同。

选择某一参考系，可以看成质点；选择另一参考系，就不可以看成质点。

答：在某些问题中，物体的形状和大小并不重要，可以忽略，可看成一个只有质量、没有大小和形状的理想的点，这样的物体就称为质点。

关于太阳、地球、分子、原子是否是质点，要视具体研究的问题而定。

例如，如果我们考察银河系或者整个宇宙的运动，那么太阳和地球的大小可以忽略，而且我们没有必要去考察他们的转动，此时它们可以被看作质点。

但是，如果我们要研究人造卫星、空间站的话，太阳和地球的大小和形状以及其自转就不能被忽略，那么它们就不能被看作质点。

1-2 西部民歌：“阿拉木汗住在哪里，吐鲁番西三百六。

”从位矢定义分析之。

分析：本题是关于参考系和坐标系选择的问题。

遇到一个问题，首先要搞清楚研究对象，然后选择一个合适的参考系，在此参考系中选择一个点作为坐标原点，建立坐标系，然后才可以定量的分析问题。

本题中心意思是选择则吐鲁番作为参照点，来定义阿拉木汗所住的位置。

答：选择地面参照系，以吐鲁番作为原点，正东方向为x 轴正方向，正北方向为y 轴正向，在地面上建立直角坐标系。

那么阿拉木汗住址的位矢为：i ?360r ?=v1-3 判断下列矢量表达式的正误：分析：本题考察矢量的运算问题。

矢量既有大小，又有方向，所以在进行矢量运算时，既要考虑矢量的大小，又要考虑矢量的方向。

（1）B A B A v v v v +=+答：× 矢量按平行四边形法则相加，而不是简单的数量相加（2）A B B A v v v v ×=×答：× 矢量相乘按右手定则，上式方程两边的矢量大小相同，方向相反。

受力分析1如图2-1-7所示，甲、乙球通过弹簧连接后用绳悬挂于天花板，丙、丁球通过细绳连接后也用绳悬挂天花板.若都在A 处剪断细绳，在剪 断瞬间，关于球的受力情况，下面说法中正确的是（）A. 甲球只受重力作用B. 乙球只受重力作用C. 丙球受重力和绳的拉力作用D. 丁球只受重力作用 分析：当在A 处剪断时两球看作一个整体，整体加速度为g,此时弹簧中的力不变, 对AB 球都会有力的作用故A B 错，绳在松弛状态不能提供力，假设绳中有拉力，则丁的加速度会大于g 而丙的加速度会小于g,则两球会相互靠近，绳则松弛，假 设不成立，故绳中无拉力・如图 所示，物体a 、b 和c 径放在水平•臬血上，水平力Fb、Fc2 2-2-8=5N=10N分别作用于物体b 、c 上，a 、b 和c 仍保持静止.以Fl 、F2、F3分别表示a 与b 、 b 与c 、c 与桌面间的静摩擦力的大小，则（ ）A Fl . F2 • F3 --------A- =5N =0 =5N一起向右作匀速直线运动，下列判断正确的是（A. B. C. D. 高一物理力学D. =0 =10N =5N 2-2-8分析：（分析方法从简单到复杂）因为a 、b 、c 均保持静止，故加速度，合外力都 为0。

先分析a 只受b 对a 的支持力，以及重力故Fl=0,再分析b, b 受到重力、 a 对b 的压力、c 对b 的支持力、Fb 、以及c 对b 的摩擦力，c 对b 的摩擦力为水 平方向，故需水平方向的力来平衡，故F2=Fb=5,方向向右。

同理在对c 分析3如图2-2-1所示, A 、B 两物体叠放在水平面上, 水平力F 作用在A 上，使两者A 、B 间无摩擦力A 对B 的静摩擦力大小为F,方向向右B 对地面的动摩擦力的大小为F,方向向右B 受到了向右的静摩擦力和向左的滑动摩擦力甲 丙图 2-1-7B. Fi=5N, F2 =5N, F?=0 4 b分析：两者一起向右作匀速直线运动，则加速度都为0,处于平衡状态。

基础物理学上册习题解答和分析－第一章习题解答和分析————————————————————————————————作者: ————————————————————————————————日期:习题一1-1．质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++其中a ，ｂ，ω均为正常数，求质点速度和加速度与时间的关系式。

分析:由速度、加速度的定义，将运动方程()r t 对时间t 求一阶导数和二阶导数，可得到速度和加速度的表达式。

解:/sin()cos()==-++v dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦１-2. 一艘正在沿直线行驶的电艇，在发动机关闭后,其加速度方向与速度方向相反，大小与速度平方成正比，即2/d d v v K t -=， 式中K 为常量．试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kxv v e-= 。

其中0v 是发动机关闭时的速度。

分析：要求()v v x =可通过积分变量替换dxdvv dt dv a ==，积分即可求得。

证：2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v=-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kxv v e -=１-3．一质点在x Ｏy 平面内运动，运动函数为22,48x t y t ==-。

(1）求质点的轨道方程并画出轨道曲线；（2)求t =1 s t =2 s 和时质点的位置、速度和加速度。

分析:将运动方程ｘ和y 的两个分量式消去参数t ，便可得到质点的轨道方程。

写出质点的运动学方程)(t r表达式。

对运动学方程求一阶导、二阶导得()v t 和()a t ，把时间代入可得某时刻质点的位置、速度、加速度。

解：(1)由2,x t =得：,2x t =代入248y t =-可得：28y x =-,即轨道曲线。

第1章习题答案1-1 解：竖直上抛运动 gH 2max20v = ()s m gH /849102008.1223max 0=⨯⨯⨯==v1-2 解：匀变速直线运动 ()()g s m t a t 259.24680.103600/1000160020<⋅=-⨯=∆-=-v v （不超过） ()()m t s t 4008.1036001000160021210=⨯⎪⎭⎫ ⎝⎛+⨯⨯=∆⨯+=v v 1-3 解：以喷嘴作为坐标原点，竖直向上作为y 轴的正向 竖直上抛运动 ()m g v H 5.348.92262220max=⨯== ()gy v y v 220-=连续性方程 ()()gyv qy v q y S 220-==任一瞬间空间上升的水流体积 ()()l gy v g q dy gy v qdy y S V H H 38.1222maxmax020020=⎥⎦⎤⎢⎣⎡--=-==⎰⎰上升下降上升V V =()l V V V 7.24=+=下降上升总1-4 解：()()bt u bt u btbt b u u dt dx v --=----⎪⎭⎫ ⎝⎛-+==1ln 1ln 11 ()()btub bt b u dt dv a -=---==11 ()00=v()()()s m v /1091.6120105.71ln 100.3120333⨯=⨯⨯-⨯-=-1-5 解：()2122212R R N rNdr s R R -==⎰ππ ()()()()m in 6939416364132256650222122==-⨯⨯=-==∆s v R R N v s t ππ()s rad r v /26.00.53.1===ω ()222/338.00.53.1s rad r v ===α1-6 解： ()s m v /37430344=+=东()s m v /31430344=-=西()s m v /3433034422=-=北N F μθ≥cos1-7 解： 因θs i nF mg N += 故 θμμθsin cos F mg F +≥ （1） θμθμs i n c o s s s mgF -≥静（2） θμθμs i n c o s k k mgF -≥动（3） 0s i n c o s ≤-θμθs sμθ1tan ≥1-8 解：()()()()()()()N a g m M F am M g m M F 676006.08.915005000=+⨯+=++=+=+-桨桨()()()N a g m F mamg F 156006.08.91500=+⨯=+==-桨绳1-9 解： r m rMm G22ω= ()()()Kg G r T G rM 261138232321069.51067.61036.136002.142/2⨯=⨯⨯⨯⎪⎭⎫ ⎝⎛⨯===-ππω1-10 解： ⎰⎰⎰-=-==ωπω20c o s td t kA kxdt Fdt I ωωωωπkAt kA -=⎥⎦⎤⎢⎣⎡-=20sin1-11 解： ()s m /500i v-=()()s m t /45sin 8045cos 800j i v +=()()s N m m t ⋅+=-=j i v v I92.778.140()215278.1492.7arctan 89.160'=-=⋅=πϕs N I ()6168.914.084584502.089.16=⨯===∆=mg F N t I F1-12 一辆停在直轨道上质量为m 1的平板车上站着两个人，当他们从车上沿同方向跳下后，车获得了一定的速度。

分析力学基础一是非判断题1.不论刚体作何种运动，其惯性力系向一点简化的主矢都等于刚体的质量与其质心加速度的乘积，方向与质心加速度的方向相反。

（√）2. 均质圆柱绕其对称轴作定轴转动，则圆柱惯性力系对于空间中平行于转轴的任意一轴的力矩之和，都是同一值。

（√）3. 因为实位移和虚位移都是约束允许的，所以实际的微小位移必定是诸虚位移中的一个。

（×）4. 虚位移原理只适用于具有理想约束的系统。

（×）5. 凡几何约束都是完整约束，完整约束未必是几何约束。

（√）二选择题1.下列约束中，非理想约束的是（B ）。

A 纯滚动，有摩擦力但无滚动摩阻。

B 有摩擦的铰链。

C 摩擦传动中两个刚性摩擦轮的接触处，两轮间不打滑，无滚动摩阻。

D 连接两个质点的不可伸长的柔索。

2. 如图所示四种情况，惯性力系的简化只有（ C ）图正确。

3. 均质细杆AB质量为m，长为L，置于水平位置，如图所示。

若在绳BC突然剪断时角加速度为α，则杆上各点惯性力的合力大小为（12mLα），方向为（垂直向上），作用点的位置在杆的（左端A ）处4. 四根等长等重的均质直杆用铰链连接起来，再把两端用铰链固定在同一水平线上，如图所示，平衡时图示两个角度α和β的关系是（ B ）。

第二(3)题图第二(4)题图A ．tan 3tan βα=； B. tan 3tan αβ= C. tan 2tan βα=; D. tan 2tan αβ=5. 图示系统中，O 处为轮轴，绳与滑轮间无相对滑动，则物块A 与物块B 的虚位移大小的比值为（ B ）。

A ．6；B ．5；C ．4；D ．3.三 填空题1. 图示平面系统，圆环在水平面上作纯滚动，圆环内放置的直杆AB 可在圆环内自由运动，A ，B 两点始终与圆环保持接触，则该系统的自由度数为（ 2 ）。

2. 轮轴质心位于O 处，对轴O 的转动惯量为O J 。

在轮轴上系有两个质量各为1m 和2m 的物体，已知此轮轴顺时针转向转动，角加速度为α，则轴承O 处的动反力Ox F =( 0 ), Oy F =（ 12()m R m r α-）。