第4章附白金汉量纲分析理论
- 格式:ppt
- 大小:224.50 KB
- 文档页数:1




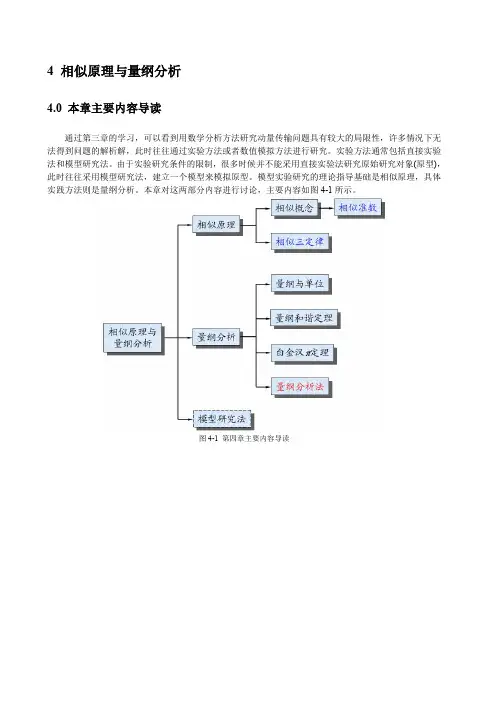


量纲分析摘要物理问题的分析与研究过程,即为准确地认识与度量该物理问题涉及的物理量,寻找并建立这些物理量之间的内在联系和定量的函数关系;从某种意义上讲,对物理量或物理规律的认识最关键的一步就是对物理量或物理量之间的内在联系进行定量的描述。
无论物理问题形式如何,其必须满足量纲一致性法则,即只有量纲相同的物理量或物理量组合才能进行对比或加减运算,因此对于任何一个物理问题或规律,其函数关系中等式两端的量纲应该完全一致;也就是说,姑且不论等式两端数值是否相等,但其量纲必定相同。
换一个角度看,我们即使不知道函数中物理量的具体数值,纯粹从量纲上进行运算和转换也可对该物理问题或规律进行初步分析;反之,我们也可以根据量纲的一致性对所给出的函数关系的正确性进行预判。
这种多个物理量量纲之间的运算包含基础衍生量纲的展开、导出独立量纲向基本量纲的转换及其基本量纲之间的运算,这种分析过程即为量纲分析。
当前物理问题涉及的量纲有很多,如不考虑无量纲物理量,物理量量纲整体可以分为三类:基本量纲(7个)、导出独立量纲(20个)和衍生量纲。
衍生量纲与基本量纲之间的联系是通过衍生量纲对应的物理量定义来建立的,如加速度量纲展开为长度量纲与时间量纲的平方之商,就利用到加速度的定义;导出独立量纲与基本量纲之间的联系则是通过应用某个物理定律来建立的,如力的量纲转换为质量量纲与加速度量纲的乘积,就应用了牛顿运动定律。
因此,量纲分析的过程也是一系列物理量定义与定律的使用及运算过程,从某种程度上讲,这是量纲分析的一个物理本质。
当前,度量单位特别是国际标准度量单位的出现,极大程度地促进了科技交流和发展,但有时也使得物理规律分析更为复杂,因为这相当于在复杂的物理问题中引入了外部基准量;对于特定物理问题而言,如果我们不采用这些基准量,而直接采用物理问题所包含的某个物理量或某几个物理量组合为度量单位,则可在一定程度上简化物理问题的分析过程。
因此,量纲分析也是排除外部基准度量单位而利用物理问题或规律涉及的物理量或物理量的组合为度量单位的一个过程,这是量纲分析的另一个物理本质。


量纲分析量纲分析是解决物理和工程问题的一个重要的科学方法和强有力的工具。
本书着重对物理和工程问题的物理机理和数量级进行分析,尽量避免运用比较复杂的数学。
在介绍了作为量纲分析的唯一的理论基础η定理以后,采用案例分析的方法,由浅入深地阐述和介绍运用量纲分析方法来解决力学中众多方面的典型问题,其中包括简单和常见问题的分析;经典问题的分析;前沿问题的分析。
始终贯彻并突出说明的是,分析问题的关键在于:在控制问题的自变量中找出问题所固有的单位系统,以此度量有关的变量,合理地抓大放小,从而导出简要结果。
全书共10章,1、序论,介绍量纲、有量纲量、无量纲量、基本量、及其导出量的定义;2、量纲分析的基本原理,论述η定理,它是量纲分析的理论基础;3、流体力学中的问题,讨论量纲分析在流体力学中的应用;4、固体力学中的问题,介绍量纲分析在固体力学中的应用;5、固体中的热传导和热应力,讨论固体中热应力的相似定律;6。
流体运动和固体变形的耦合问题,采用量纲分析讨论流体运动和固体变形耦合的相关案例;7。
液体-弹塑性体模型,并以该模型为基础,讨论在爆炸和高速冲击的实际问题中的控制参数和相似性参数;8。
爆炸的相似律,讨论爆炸波的传播规律,工程技术应用中爆炸的基本原理和相似律,主要涉及爆炸成形、爆炸焊接和爆破;9。
高速冲击的相似律,介绍由三种类型反坦克弹产生的装甲动态破坏、射流和薄片的拉伸断裂、煤与瓦斯突出;10。
数学模拟中的归一化,数学模拟是指:不同类型的物理现象,可以用共同的数学语言来描述的一类模拟,数学模拟的关键在于归一化,即要选择合适的单位系统。
本书适合大学生和研究生阅读,对于物理、力学、工程技术和应用数学相关领域的研究人员、工程师、和研究生来说,是一本很有价值的参考书。
吴永礼,研究员(中国科学院力学研究所)。


量纲和谐原理我们经常遇到许多物理量,如长度、时间、质量、力、速度、密度及动量等。
它们的名称、记号和量纲如表所示。
表1 流体力学中常见物理量的量纲速度v 表示单位时间内所经历的距离,它的单位是[米/秒]。
距离是长度l ,它的量纲是[L ],而时间t 的量纲是[T ],故速度v 的量纲是[1LT -]。
动量是质量m 和速度v 之积。
质量的量纲是[M ],故动量的量纲是[1MLT -]。
如果我们选定三个相对对立的,例如长度l 的量纲[L ]、时间t 的量纲[T ]、质量m 的量纲[M ]为基本量纲,那么其他物理量的量纲都可用这三个基本量纲来表示。
如表5-1中所示,例如,加速度a 的量纲可表示为[2LT -],力F 的量纲可表示为[2LMT -]。
当我们把一些物理量进行组合、分析或作比较时,用量纲表示就比较便利。
如果我们要写出一个流体微团的运动方程F ma =∑式子左边是作用在微团的各力和,它可以包括:重力W 、压力P 、粘滞τ、力弹性力E等;右边是微团的惯性力ma。
于是得到+++W P E ma t =(5-1)上式中的每项都是力,所以各项的量纲都是[2LMT -]。
又如,关于理想流体的伯努利方程2++=2v p z H g gr 表示流管中三项能头之和保持常数,即等于总能头H 。
每项的单位都是米,故它们的量纲都是[L]。
不仅如此,在力学上任何有物理意义的方程或关系式,每一项的量纲必定相同。
这称为力学方程的量纲和谐性原理,又称为“量纲齐次性规律”。
量纲和谐原理是由傅里叶1822年提出来的,它是量纲分析法中具有基本重要性的一个概念,也是量纲分析法的理论基础,并可具体表达成:只有相同类型的物理量才能相加减,也就是相同量纲的物理量才可以相加减或比较大小;不同类型的物理量相加减没有任何意义。
例如,速度可以和速度相加减,但绝不可以加上粘性系数或压力。
当然,相同量纲和不同单位的物理量之间是可以相互加减和比较大小的,因为只要将其单位稍加换算即可完成。
量纲分析-量纲分析量纲分析-正文白金汉定理白金汉(Buckingham) π定理:对于某个物理问题,如果存在 n 个变量,其中有 m 个基本量,则存在 n-m 个独立的无量纲参数,即可以将 n 个变量组合成 n-m 个无量纲π数。
以简单摆运动为例,这个物理问题存在5个变量:摆球的质量 m、摆线的长度 l、摆角θ、时间 t 和重力加速度 g,其中有3个基本量:质量、长度和时间,则存在2个独立的无量纲π数,如和Π2 = θ。
自然科学中一种重要的研究方法,它根据一切量所必须具有的形式来分析判断事物间数量关系所遵循的一般规律。
通过量纲分析可以检查反映物理现象规律的方程在计量方面是否正确,甚至可提供寻找物理现象某些规律的线索。
概述各种物理量之间存在着关系,说明它们的结构必然由若干统一的基础成分所组成,并按各成分的多寡形成量与量间的千差万别,正如世间万物仅由百余种化学元素所构成。
物理量的这种基本构成成分统称为量纲。
由于物理学研究物质在时空中的演化和运动,所以一切定量问题最终离不开质量、时间和长度这三种基本量。
因而最适宜于选取M、T、L做为这三种基本量的量纲。
一切其他导出量的量纲可按定义或客观规律表成这三种基本量的量纲组合。
基本量有多种取法,在力学中通常取质量、长度和时间为基本量,其他量(例如速度、力等)可按一定规则由基本量导出。
任何其他三类量纲互相独立的导出量也可作为基本量。
性质上完全不同的两种物理量可具有相同的量纲,例如功和力矩就是如此。
任何正确反映物理现象规律的方程,其两端各项都必须具有相同的量纲。
物理量的大小,除按个数计的外,通常由一个或几个实数连同所采用的单位表示。
这种数一般称为“名数”,意为不标明单位名称就没有意义的数。
名数的实数值可以随不同的对象处于不同的时间或空间而不同。
这是由于对象不同或本身发生变动而引起的实质变化。
但名数值还会随所采用的单位大小而改变,而且是单位大小的连续函数。
因为单位的大小可以任选,所以名数值的上述改变不是客观的实质变化。