下载文档原格式
1、结合个人的使用体会，谈谈显卡的主要技术指标主要技术指标：最大分辨率：当一个图像被显示在屏幕上时，它是由无数小点组成的，它们被称为像素(Pixel)。
最大分辩率是指显示卡能在显示器上描绘点的最大数量，一般以“横向点数X 纵向点数”表示。
色深：像素描绘是的是屏幕上极小的一个点，每一个像素可以被设置为不同的颜色和亮度。
像素的每一种状态都是三种颜：红、蓝、绿所控制，当它们都处于最大亮度时，像素就呈现为白色,；反之，像素为黑色。
像素的颜色数称为色深，该指标用来描述显示卡能够显示多少种颜色，一般以多少色或多少bit色来表示，如8bit色深可以显示256种颜色，16bit色深可显示65536种颜色，称为增强色，24bit色深可以显示16M 种颜色,称为真颜色，所以色深的位数越高,所能看见的颜色就越多，屏幕上画面的质量就越好。
但色深增加时，也增大了显示卡所要处理的数据量，这就要求显示卡配有更大显示内存并具有更高的转换速率。
刷新频率：刷新频率是指图像在显示器上更新的速度，也就是图像每秒在屏幕上出现的帧数，单位为Hz （赫兹）。
刷新频率越高，屏幕上图像的闪烁感就越小，图像越稳定，视觉效果也越好。
一般刷新频率在75Hz以上时，人眼对影像的闪烁才不易查觉。
这个性能指标主要取决于显示卡上RAMDAC的转换速度。
显存：如果说显存带宽决定了显卡的性能，那么显存位宽就决定了显存带宽，因为在相同频率下，64位显存的带宽只有128位显存的一半，当遇到大量像素渲染工作时，因为显存位宽的限制会造成显存带宽的不足，最直接的后果就是导致传输数据的拥塞，速度明显下降屏幕更新频率(Vertical刷新Rate)指显示器每秒能对整个画面重复更新的次数，若此数值为72Hz，表示显卡每秒将送出72张画面讯号给显示器。
在显卡中的渲染管线包括很多，比如像素渲染管线、纹理渲染管线、顶点渲染管线等等，它们在显卡中起到各自的作用。
体会：同型号同容量的情况下，可以比较：1.显存位宽（越大越好）以及显存用料比如GDDR1/GDDR2/GDDR3；2.核心频率和显存频率（越高越好）如：256bit/256M与128bit/256M；3.显卡的速度，就是几点几纳秒（越小越好），一般显卡的速度只有查显卡的说明书才能得出。
西安电子科技大学出版社《计算方法》任传祥等编著第九章计算方法上机参考答案实验一，算法一#include <stdio.h>#include <math.h>double I0=log(6)/log(5),I1;int n=1;main (){while(1){I1=1.0/(n)-I0*5.0;printf("%d %lf\n", n,I1);if(n>=20)break;elseI0=I1;n++;}}实验一，算法二#include <stdio.h>#include <math.h>double I0=(1/105.0+1/126.0)/2,I1;int n=20;main (){printf("%d %lf\n", n,I0);while(1){I1=1.0/(5.0*n)-I0/5.0;printf("%d %lf\n", n-1,I1);if(n<2)break;elseI0=I1;n--;}}实验二，二分法#include <stdio.h>#include <math.h>#define esp 1e-3double f(double x);main (){double a=1,b=2,x;while(fabs(b-a)>esp){x=(a+b)/2;printf("x=%lf\n",x);if(f(x)==0)break;elseif(f(x)*f(a)<0)b=x;elsea=x;}}double f(double x){return pow(x,3)-x-1;}实验二，牛顿迭代法#include<stdio.h>#include<math.h>double f(double x);double f1(double x);#define esp 1e-3void main(){double x0 = 1.5, x1;x1 = x0 - f(x0) / f1(x0);printf("x=%lf\n", x1);x0 = x1;x1 = x0 - f(x0) / f1(x0);printf("x=%lf\n", x1);while (fabs(x1 - x0)>esp){x0 = x1;x1 = x0 - f(x0) / f1(x0);printf("x=%lf\n", x1);} }double f(double x){return pow(x, 3) - x - 1;} double f1(double x){return 3 * x*x - 1;}弦割法#include<stdio.h>#include<math.h>double f(double x);#define esp 1e-3void main(){double x0 = 1.5, x1=2.0,x2;do{ x2=x1 - (x1-x0)*f(x1) /(f(x1)-f(x0));x0=x1;x1=x2;printf("x=%lf\n", x1);}while (fabs(x1 - x0)>esp);{printf("x=%lf\n", x1);}}double f(double x){return pow(x, 3) - x - 1;}实验3#include <stdio.h>/*列主元高斯消去法*/#include <math.h>float x[3],temp,max;float A[3][4]={10,-2,-1,3,-2,10,-1,15,-1,-2,5,10},c[3][4]={10,-2,-1,3,-2,10,-1,15,-1,-2,5,10}; int n=3,i,k,j,m;void main(){for(i=0;i<n;i++){max=A[i][i];k=i;for(j=j+1;j<n;j++){{max=fabs(A[j][i]);k=j;}}if(k!=i){for(j=i+1;j<=n;j++){temp=A[i][j];A[i][j]=A[k][j];A[k][j]=temp;}}for(j=i+1;j<n;j++)for(m=i+1;m<=n;m++){c[j][m]=c[j][m]+(-c[j][i]/c[i][i])*c[i][m];}}for(i=n-1;i>=0;i--){temp=0.0;for(j=n-1;j>=i+1;j--)temp=temp+c[i][j]*x[j];x[i]=(c[i][n]-temp)/c[i][i];}printf("x[1]=%f\nx[2]=%f\nx[3]=%f\n",x[0],x[1],x[2]);实验四，拉格朗日插值#include<stdio.h>int n=5,i,j;double l,L=0,X=0.5;main(){double x[5]={0.4,0.55,0.65,0.8,0.9};doubley[5]={0.41075,0.57815,0.69675,0.88811,1.02652}; for(i=0;i<n;i++){l=y[i];for(j=0;j<n;j++){if(j!=i)l=l*(X-x[j])/(x[i]-x[j]); } L=L+l;}printf("%lf\n",L);return 0;} X=0.5 X=0.7 X=0.85牛顿插值法#include<stdio.h>#include<math.h>main(){double x[5]={0.4,0.55,0.65,0.8,0.9};doubley[5]={0.41075,0.57815,0.69675,0.88811,1.02652};int n=5,i,j;double z;printf("input z\n");scanf("%lf",&z);double a[5][5];for(i=0;i<5;i++)a[i][0]=y[i];for(i=1;i<5;i++)for(j=i;j<5;j++)a[j][i]=(a[j][i-1]-a[j-1][i-1])/(x[j]-x[j-i]);double N=a[0][0],temp=1.0;for(i=1;i<n;i++){temp=temp*(z-x[i-1]);N=N+a[i][i]*temp;}printf("N=%lf\n",N);return 0;}实验五曲线拟合#include <stdio.h>#include <math.h>float x[5]={1,2,3,4,5};float y[5]={7,11,17,27,40};float A[2][3],c[2][3];float z[2],temp,max;int i,j,k,m;int n=2;void main(){for(i=0;i<5;i++){c[0][0]=A[0][0]+=1;c[0][1]=A[0][1]+=x[i];c[0][2]=A[0][2]+=y[i];c[1][0]=A[1][0]+=x[i];c[1][1]=A[1][1]+=x[i]*x[i];c[1][2]=A[1][2]+=x[i]*y[i];}/* for(i=0;i<2;i++){printf(" %lf %lf %lf\n",A[i][0],A[i][1],A[i ][2]);}*/for(i=0;i<n;i++){max=A[i][i];k=i;for(j=j+1;j<n;j++){if(fabs(A[j][i])>max){max=fabs(A[j][i]);k=j;}} if(k!=i){for(j=i+1;j<=n;j++){temp=A[i][j];A[i][j]=A[k][j];A[k][j]=temp;}}for(j=i+1;j<n;j++)for(m=i+1;m<=n;m++){c[j][m]=c[j][m]+(-c[j][i]/c[i][i])*c[i][m];}}for(i=n-1;i>=0;i--){temp=0.0;for(j=n-1;j>=i+1;j--)temp=temp+c[i][j]*z[j];z[i]=(c[i][n]-temp)/c[i][i];}printf("a=%f\nxb=%f\n",z[0],z[1]); }实验六数值积分/*梯形*/#include<stdio.h>#include<math.h> double f(double x); main(){double x[10],y[10];double h,b=1,a=0,I;int n,i;printf("n\n");scanf("%d",&n);h=(b-a)/n;for(i=0;i<=n;i++){x[i]=a+(i*h);y[i]=f(x[i]);}I=f(a)+f(b);for(i=1;i<=n-1;i++){I=I+2*y[i];}I=(h/2)*I;printf("%lf",I);}double f(double x){double f;f=1.0/(1.0+(x*x));return(f);}/*辛普森*/#include<stdio.h>#include<math.h>double f(double x);main(){double x[30],y[30];double h,b=1,a=0,I;int n,i;printf("n\n");scanf("%d",&n);//点乘2扩展h=(b-a)/n;x[10]=1;y[10]=f(x[10]);for(i=0;i<n;i++){x[2*i]=a+(i*h);y[2*i]=f(x[2*i]);x[2*i+1]=a+(i+(1.0/2.0))*h;y[(2*i)+1]=f(x[(2*i)+1]);}I=f(a)+f(b);for(i=0;i<n;i++){I=I+4*y[(2*i)+1];}for(i=1;i<n;i++){I=I+2*y[2*i];}I=(h/6)*I;printf("%lf\n",I);}double f(double x){double f;f=1.0/(1.0+(x*x));return(f);}/*梯形*//*辛普森*/。
第二次试验一、问题：Matrix-chain product分析：本题是矩阵链乘问题，需要求出最优括号化方案。
即在矩阵的乘法链上添加括号来改变运算顺序以使矩阵链乘法的代价降低。
可以分析该链乘的一个子段总结一些结论。
假设m[i,j]表示A i*…*A j的链成需要进行的乘法次数（假设j-i足够大），我们可以将A i*…*A j分为两段进行计算：（A i*…*A k）*（A k+1*…*A j）可以得出m[i,j]的递推公式可以得出，当i=j的时候，m[i,j]=0。
当i<j的时候。
k的取值范围是i到j-1，对于k的每一个取值都可以得到一个m[i,j]的值，取出最小值即时m[i,j]的最优化方案。
递推公式如下：可以根据上式得到一个递归算法。
本题即是求m[1,n]的值。
用二维数组m存储m[i,j]的值，用二维数组s来储存应当分割的位置。
以本题中第一个矩阵a) <3, 5, 2, 1,10>为例，可以得出如下矩阵：通过m数组可以得出最少的乘法次数，通过s数组可以输出最优方案。
遇到的问题：在输出s数组的结果的时候仍然需要递归调用，需要合适的控制递归的条件。
总结：在矩阵链乘问题中可以看出，动态规划结合递归的思想可以快捷的解决很多问题。
本题中，重点是归纳出m[i,j]的递推公式。
二、问题：Longest Common Subsequence分析：本题即是最长公共子序列问题。
假设有序列A[m]和序列B[n]，显然，对于每一个[i,j]，都对应着一个公共子序列的长度。
假设长度为c，就可以得到一个二维数组c[m,n]。
对于c[i,j]，当Ai=Bj的时候，问题就转变为求A[1..i-1]和B[1..j-1]的公共子序列长度的问题，所以c[i，j]的长度就是c[i-1，j-1] + 1;同理，当Ai != Bj的时候，c[i,j]应该在c[i-1,j]与c[i,j-1]中取最大值。
另外，当i或者j等于0的时候，显然c的值为0。
关于中国南海岛礁巡航路线方案的探讨姓名：刘发强学号：140201990442016年11月8日摘要南海岛礁巡航路线方案的确定实质上是一个求取平面有障碍区域两点之间最短路径问题和TSP问题的混合。
针对前者，本文借助ESPO算法的思想，将外国非法侵占岛礁所确定的12海里敏感区域抽象为正多边形，在对所有顶点及起始点之间任一条路径的合法性判定（借助计算几何中点、线段、多边形的位置关系）之后，利用Dijkstra算法生成障碍密集区（南沙群岛）我方任意两岛礁之间的最短路径，后对我方全体（西沙、南沙、中沙）岛礁利用Floyd算法生成最短路径完全图的邻接矩阵，为后续处理奠定基础。
针对后者，利用自适应的蚁群算法求取最优解，经检验效果较好。
同时借助openCV 提供的图像处理和画图函数对算法的运行和结果进行了可视化呈现，易于理解调试。
理论上，本文的解决方案对于这类问题有很广泛的适用性。
关键词：TSP问题；ESPO算法；Dijkstra算法；Floyd算法；openCV；蚁群算法；算法可视化绪论随着中国海权意识的逐步觉醒和军事力量的日益强大以及美国重返亚太战略的实施，南海态势在多方的博弈下波谲云诡，不安定不稳定性极大。
为了维护我国的主权和领土完整，对我国实际控制的岛礁进行周期性的补给和巡航势在必行。
因此，在周围情况极其复杂的南海确定一个最优的巡航路径非常关键。
本文主要借助ESPO算法和蚁群算法对我国南海实际控制的包括西沙、中沙、部分南沙在内的23个岛礁进行了路径规划，比较圆满的解决了上述问题，且具有良好的可扩展性和适用性。
本文的基本假设：1、地球表面近似为球面，在经线上，每纬度约111千米，在纬线上，每经度约为111*cosθ千米，其中θ为纬度。
由于所考查区域（纬度从东经111°到东经117°，北纬8°到北纬18°）面积相对较小且在低纬度，故近似为平面即每经度111千米。
利用百度地图的测距工具和坐标拾取系统得出的结果与对平面上两点欧几里得距离相比最大相对误差低于1%，这对于本问题的解决足够准确。
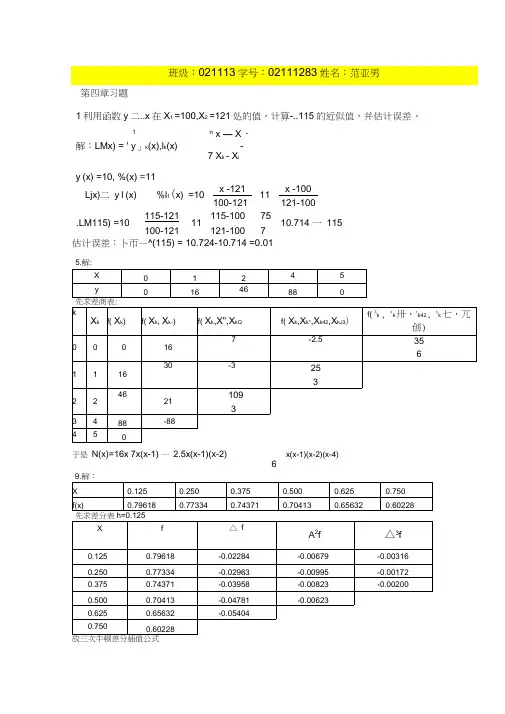
第四章习题1利用函数y 二..x 在X 1 =100,X 2 =121处的值，计算-..115的近似值，并估计误差。
1nx — X ・解：LMx) = ' y 」k (x),l k (x) -7 X k - X iy °(x) =10, %(x) =11估计误差：卜帀—^(115) = 10.724-10.714 =0.01于是 N(x)=16x 7x(x-1) 一 2.5x(x-1)(x-2)x(x-1)(x-2)(x-4)6Ljx)二 y °l °(x) %l 1(x) =10 x -121 100-121 11x -100121-100.LM115) =10115-121 100-121 11 115-100 121-100 757 10.714 一 115N°(0.125 0.125t) =0.79618— 0.02284t— 0.003395t(t -1) —0.000527t(t — 1)(t - 2) 当0.125+0.125t=0.1581 时，t=0.2648 代入上式得f(0.1581)=0.790615当0.125t+0.125=0.636 时，t=4.088 代入上式得f(0.636)=0.646062上机作业例1:已知函数表：xi 0.56160 0.56280 0.56401 0.56521yi 0.82741 0.82659 0.82577 0.82495用三次拉格朗日插值多项式求x=0.5635时的函数近似值C语言程序设计：# in clude<stdio.h>float Lagrange(float x[],float y[],float xx,int n){int i,j;float *a,yy=0;a=new float[ n];for(i=0;i<=n _1;i++){a[i]=y[i];for(j=0;j<=n _1;j++)if(j!=i) a[i]*=(xx-x[j])/(x[i]-x[j]);yy+=a[i];}delete a;return yy;}void mai n(){float x[4]={0.56160,0.56280,0.56401,0.56521};float y[4]={0.82741,0.82659,0.82577,0.82495};float xx=0.5635,yy;yy=Lagra nge(x,y,xx,4);prin tf("x=%f,y=%f\n",xx,yy);}运行结果：x=0.563500y=0.826116g *C:\DocuMents and Settings\Ad>inistrator\Debug\Cpp1.exe 1^0.563500/9=0.826116Press any key to cont in Lie例2:已知函数表xi 0.4 0.55 0.65 0.8 0.9yi 0.41075 0.57815 0.69675 0.88811 1.02652 用牛顿插值多项式求M(0.596)和2 (0.895 )。
上机报告一.最速下降法算法简述：1.在本例中，先将最速下降方向变量赋一个值，使其二范数满足大于ε的迭代条件，进入循环。
2.将函数的一阶导数化简，存在一个矩阵，将其hesse矩阵存在另一个矩阵。
依照公式求出α，进而求出下一任迭代的矩阵初值。
循环内设置一个计数功能的变量，统计迭代次数。
3.求其方向导数的二范数，进行判别，若小于ε，则跳出循环，否则将继续迭代。
4.显示最优解，终止条件，最小函数值。
心得体会：最速下降法的精髓，无疑是求梯度，然后利用梯度和hesse矩阵综合计算，求解下一个当前最优解。
但是，要求函数是严格的凸函数，结合严格凸函数的大致图像，这就给初值的选取提供了一点参考。
例如在本例中，由于含有两个变量的二次方之和，结合大致图像，想当然的，初值的选取应当在原点附近；又因为变量的二次方之和后面，还减去了变量的一次形式和一次混合积，所以初值的选取应该再向第一象限倾斜。
综合以上考量，第一次选取（1,1）作为初值，判别精度方面，取到千分位，暂定为0.001。
运行以后，结果显示迭代了25次，最优解为（3.9995，1.9996），终止条件为5.4592e-04，目标函数为-8.0000。
这个结果已经相当接近笔算结果。
整体的运行也比较流畅，运算速度也比较快。
第二次取值，决定保留判别精度不变，将初值再适当向第一象限倾斜，取（2,2）作为初值，运行后，显示只迭代了11次！最优结果显示（3.9996，1.9997），终止条件为3.6204e-04，最优解-8.0000。
可见，最优结果更接近理想值，终止条件也变小了，最关键的是，迭代次数减少至第一次的一半以下！这说明以上初选取的方向是对的！第三次再进行初值细化，判别精度仍然不变，初值取（3,3）。
结果令人兴奋，只迭代了四次！最优解已经显示为（4.0000,2.0000），终止条件为2.4952e-04，目标函数-8.0000。
第四次，判别精度不变，取初值（4,4）。
西电数电大作业本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March数电作业设计报告一、八人抢答电路设计要求：1.抢答器编号1到8，相应的抢答器被按下时其编号会在数码管上显示，此时其他抢答器的操作将被封锁；2.具有每次抢答之前的手动清零功能；3.清零后新一轮抢答开始，倒计时30秒，若30内无抢答器被按下，则红灯亮一下示意此次抢答无效；具体结构展示：1）抢答电路如图：初始状态：按下抢答器按键后：按下清零按键后：首先将八个抢答器的状态等效一组状态码，采用74LS148（8线-3线优先编码器）进行编码输出，输入端选取0到7位对应八个抢答器，由于输出范围为000~111，所以输出端加74LS283（超前进位加法器）将输出每项加0001，此时输出范围为0001~1000，输送给数码管以显示组号；为了实现当有抢答器按下是其他抢答器被封锁的功能，采用74LS175（四D触发器）以及一个D触发器以及一个四输入与非门构成锁存器，连接方式如图。
当有抢答器被按下的时候编码器从EO 端端同时产生一个上升脉冲，送入4D触发器的时钟端，为了让时钟捕捉到触发器输入端的序列，使用D触发器对EO端的脉冲进行延时。
最终当信号序列送入数码管后，四个Q输出端通过一个与非门连接编码器的使能端EI，当有信号序列输入时，与非门输出为1，编码器被禁止工作；需要清零时按一下与触发器clear端相连的开关，此时四D触发器Q输出端全部置1，与非门输出为0，编码器工作，等待接收信号；2）计时电路如图：采用两片74LS160（十进制计数器）整体置数法构成模三十计数器，计数范围为000000001 ~ 0011 0000，输出端连接数码管显示。
三十秒计数结束的时若仍没有抢答器被按下，则红灯亮，此次抢答无效。
3）总电路如图：抢答电路与计时电路连接的关键在于：1.四D触发器Q输出端进过与非门后再过一个反相器与两片计数器的一个允许控制端相连，以达到控制计数器是否工作的目的；2.四D触发器清零端与计时器的反馈相与之后送给置数端，以确保每次清零后计数从零开始。
算法设计大作业寻找多数元素班级：021151学号：02115037姓名：隋伟哲(1)问题提出：令A[1,2,…n]是一个整数序列，A中的整数a如果在A中出现的次数多余⎣n/2⎦，那么a称为多数元素。
例如在序列1,3,2,3,3,4,3中，3是多数元素，因为在7个元素中它出现了四次。
有几个方法可以解决这个问题。
蛮力方法是把每个元素和其他各个元素比较，并且对每个元素计数，如果某个元素的计数大于⎣n/2⎦，就可以断定它是多数元素，否则在序列中就没有多数元素。
但这样比较的次数是n(n-1)/2=Θ(错误！未找到引用源。
),这种方法的代价太昂贵了。
比较有效的算法是对这些元素进行排序，并且计算每个元素在序列中出现了多少次。
这在最坏情况下的代价是Θ(n 错误！未找到引用源。
).因为在最坏情况下，排序这一步需要Ω(n 错误！未找到引用源。
)。
另外一种方法是寻找中间元素，就是第⎡n/2⎤元素，因为多数元素在排序的序列中一定是中间元素。
可以扫描这个序列来测试中间元素是否是多数元素。
由于中间元素可以在Θ（n）时间内找到，这个方法要花费Θ（n）时间。
有一个漂亮的求解方法，它比较的次数要少得多，我们用归纳法导出这个算法，这个算法的实质是基于下面的观察结论。
观察结论：在原序列中去除两个不同的元素后，原序列的多数元素在新序列中还是多数元素。
这个结论支持下述寻找多数元素候选者的过程。
将计数器置1，并令c=A[1]。
从A[2]开始逐个扫描元素，如果被扫描的元素和c相等。
则计数器加1，否则计数器减1.如果所有的元素都扫描完并且计数器的值大于0，那么返回c作为多数元素的候选者。
如果在c和A[j](1<j<n)比较式计数器为0，那么对A[j+1,…n]上的过程调用candidate过程。
算法的伪代码描述如下。
(2)算法Input: An array A[1…n] of n elements;Output: The majority element if it exists; otherwise none;1. c←candidate(1);2. count←0;3. for j←1 to n4. if A[j]=c then count←count+1;5. end for;6. if count>⎣n/2⎦ then return c;7. else return none;candidate(m)1. j←m; c←A[m]; count←1;2. while j<n and count>03. j←j+1;4. if A[j]=c then count←count+1;5. else count←count-1;6. end while;7. if j=n then return c;8. else return candidate(j+1);（3）代码//Majority.cpp#include<iostream>using namespace std;int Candidate(int *A, int n, int m);int Majority(int *A, int n);int main(){int n;cout << "please input the number of the array: ";cin >> n;int *A;A = (int *) malloc(n*sizeof(int) );cout << "please input the array: ";for (int i = 0; i < n; i++)cin >> A[i];if (Majority(A, n) != 'N')cout << "the majority is: " << Majority(A, n);elsecout << "the majority element do not exist! ";free(A);cin.get();cin.get();return 0;}int Majority(int *A, int n){int c = Candidate(A, n, 0), count = 0;for (int j = 0; j < n; j++)if (A[j] == c)count += 1;if (count > n / 2)return c;else return'N';}int Candidate(int *A, int n, int m){int j = m, c = A[m], count = 1;while (j < n && count>0){j += 1;if (A[j] == c)count += 1;else count -= 1;}if (j == n)return c;else return Candidate(A, n, j + 1); }（4）运行结果（5）设计实例首先输入数据的个数n=7，然后依次读入n个数（1，3，2，3，3，4，3）。
习题11. x1=4.8675 x1有5位有效数字；x2=4.08675 x2有6位有效数字；X 3=0.08675 x3有4位有效数字；x4=96.4730 x4有6位有效数字； X 5=96×105 x5有2位有效数字；x6=0.00096 x6有2位有效数字。
8.解: y n =5y n-1-2 n=1,2, (1)y 0= 3在计算y 0时有舍入误差，设为e 0,并设求得的y 0的近似值y 0,即e 0= y 0 -y 0，所以，yn = 5y n-1-2 n=1,2,… (2) y 0=y 0-e 0由（1）-（2）得：y n - y n =5(y n-1- y n-1)所以y n -y n =5ne 0 n=1,2,…所以e 10=510e 0=510( 3 -1.73)=20027.42 所以这个计算过程不稳定。
10.解：f(x)=8x 5-0.4x 4+4x 3-9x+1=(8x 4-0.4x 3+4x 2-9)x+1=((8x 3-0.4x 2+4x)x-9)x+1=(((8x 2-0.4x+4)x-9)x+1 =((((8x-0.4)x+4)x-9)x+1b 0=8；b 1=8x-0.4=8×3-0.4=23.6； b 2= b 1x+4=23.6×3+4=74.8； b 3= b 2x=74.8×3=224.4;b 4= b 3x-9=224.4×3-9=664.2; b 5= b 4x+1=664.2×3+1=1993.6; 所以f(3)= b 5=1993.6.8 -0.4 4 0 -9 1X=3 24 70.8 224.4 673.2 1992.6 8 23.6 74.8 224.4 664.2 1993.6 所以f(3)=1993.6. 习题21. 证明：令f(x)=1-x-sinx,则f ′(x)=-1-cosx>0,所以f （x ）在区间[0,1]中连续且严格单调递增。
又因为f(0)=1,f(1)=-sin1,即f(0)f(1)＜0,所以方程1-x-sinx=0在区间[0,1]中有且只有一个根。
由1／2k+1=12 ×10-3得：k ≥3ln10ln2≥9.965所以使用二分法求误差不大于12×10-3的根需要二分10次。
2. 用简单迭代法求e x-4x=0的根，精确至四位有效数字解：设f(x)= e x -4x,则f ′(x)= e x-4。
因为f(0.35)= e 0.35-4×0.35=0.019068,f(0.38)= e 0.38-4×0.38=-0.057715,f(0.35)f(0.38)<0且当x ∈[0.35,0.38]时f ′(x)= e x-4<0即f(x)在[0.35,0.38]上单调递减。
所以f(x) 在[0.35,0.38]上有且仅有一个根。
将方程e x -4x=0改写成等价形式x= e x /4,于是有φ（x ）= e x /4，则φ′（x ）= e x/4。
当x ∈[0.35,0.38]时，φ（x ）∈[φ(0.35),φ(0.38)]=[0.354767,0.365571]包含于[0.35,0.38]且︱φ′（x ）︱≦︱φ′（0.38）︱= e 0.38/4=0.365571<1。
所以对任意x 0∈[0.35,0.38]，迭代格式x k+1= e k/4,k=0,1,2,…收敛,取x 0=0.35,则所以x *≈0.3574，其误差不超过12 ×10-4。
f(x k )…所以x ≈2.095。
习题33.（1）解： 2 -1 3 1 r 2+（-2）r 1 2 -1 3 1 4 2 5 4 0 4 -1 2 1 2 0 7 r 3+（-12 ）r 1 0 52 -32 132r 3+（-58）r 2 2 -1 3 10 4 -1 2 00 -78 214因而我们得到与原方程组同解的三角方程组为 2x 1-x 2+3x 3=1 4x 2-x 3=2 -78 x 3=214通过回代过程易得解为：x 1=9,x 2=-1,x 3=-65. 解： 2 -1 3 1 r 1 r 2 4 2 5 4 4 2 5 4 2 -1 3 1 1 2 0 7 1 2 0 7r 2+（-12）r 1 4 2 5 40 -2 12-1r 3+（-14 ）r 1 0 32 -54 6r 3+34 r 2 4 25 40 -2 12 -10 0 -78 214因而我们得到与原方程组同解的三角方程组为4x 1+2x 2+5x 3=4 -2x 2+12 x 3=-1-78 x 3=214通过回代过程易得解为：x 1=9,x 2=-1,x 3=-61. 利用函数y=x 在x 1=100,x 2=121处的值，计算115 的近似值，并估计误差。
解：y 1=100 =10, y 2=121 =11.取x 1和x 2为节点作一次插值，得 L 1(x)=x-121100-121 ×10 + x-100121-100×11则 L 1(115)= 115-121100-121 ×10 + 115-100121-100 ×11= -6-21 ×10 + 1521 ×11= 27 ×10 + 57 ×11= 257=10.7142857≈115误差：y=x ，y ′=12 x -0.5, y ″=- 12 × 12 x -1.5=- 14 x -1.5,115 - L 1(115)= 12 ×(- 14ξ-1.5)×(115-100)×(115-121) 100＜ξ＜121所以|115 - L 1(115)|≤12 ×|(- 14 ×100-1.5)|×|(115-100)×(115-121)|= 18 ×11000 ×15×6=0.01125 2. 给出函数表x 0 1 2 4 5y 0 16 46 88 0 试求各阶差商，并写出牛顿插值多项式。
解：差商表k x k f[x k ] f[x k ,x k+1] f[x k ,x k+1,x k+2] f[x k ,x k+1,x k+2,x k+3] f[x k ,x k+1,x k+2,x k+3,x k+4] 0 0 0 16 7 - 52 - 761 1 16 30 -3 - 2532 2 46 21 - 10933 4 88 -88 4 5 0所以N 4=0+16（x-0）+7(x-0)(x-1) - 52 (x-0)(x-1)(x-2) - 76 (x-0)(x-1)(x-2)(x-4)=16x+7x(x-1) - 52 x(x-1)(x-2) - 76x(x-1)(x-2)(x-4)3. 给定数据表x 0.125 0.250 0.375 0.500 0.625 0.750 f(x) 0.79618 0.77334 0.74371 0.70413 0.65632 0.60228 使用三次牛顿差分插值公式计算f(0.1581)及f(0.636).解：x k f k Δf k Δ2f k Δ3f k Δ4f k Δ5f k 0.125 0.79618 -0.02284 -0.00679 -0.00316 0.00488 -0.00460 0.250 0.77334 -0.02963 -0.00995 0.00172 0.00028 0.375 0.74371 -0.03958 -0.00823 0.00200 0.500 0.70413 -0.04781 -0.00623 0.625 0.65632 -0.05404 0.750 0.60228N 3(0.125+0.125t)=0.79618-0.02284t-0.00679t(t-1)-0.00316t(t-1)(t-2) N 3(0.1581)= N 3(0.125+0.125×0.2648)= 0.79618-0.02284×0.2648-0.00679×0.2648×(0.2648-1)-0.00316×0.2648×(0.2648-1)×(0.2648-2)=0.790N 3(0,636)=N 3(0.125+0.125×4.088)=0.79618-0.02284×4.088-0.00679×4.088×(4.088-1)-0.00316×4.088×(4.088-1)×(4.088-2)=0.534 习题61、（1）求积分公式()⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-≈⎰-313111f f dx x f 有几次代数精度。
解：当()1=x f 时，左边=⎰-111dx =2，右边=1+1=2，左边等于右边；当()x x f =时，左边=⎰-11xdx =0，右边=03131=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-，左边等于 右边；当()2x x f =时，左边=⎰-112dx x =32，右边=32313122=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-，左边 等于右边；当()3x x f =时，左边=⎰-113dx x =0，右边=0313133=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-，左边等 于右边；当()4x x f =时，左边=⎰-114dx x =52，右边=52313144=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-，左边 不等于右边；则有：所给的积分公式的代数精度为3。
2、确定下列求积公式中的特定参数，使其代数精度尽量高，并指出 其代数精度的次数。
（3）()()()()1012111f f f dx x f ααα++-≈⎰-解：当()1=x f 时，左边=2111⎰-=dx ，右边=210ααα++；当()x x f =时，左边=011⎰-=xdx ，右边=20αα+-；当()2x x f =时，左边=32112⎰-=dx x ，右边=20αα+； 则要使求积公式的代数精度为2，当且仅当32022020210=+=+-=++ααααααα 解方程组有：313431210===ααα将所得的三个值代入原式有：()()()()13103413111f f f dx x f ++-≈⎰-当()3x x f =时，左边=0113⎰-=dx x ，右边=()(),013113133=+-⨯左边等于右边； 当()4x x f =时，左边=52114⎰-=dx x ，右边=()()3213113144=+-，左边不等于右边；综上所述，该求积公式的代数精度为3。
