西安电子科技大学出版社计算方法上机答案
- 格式:doc
- 大小:244.70 KB
- 文档页数:7

(完整版)数值计算⽅法上机实习题答案1.设?+=105dx xx I nn ,(1)由递推公式nI I n n 151+-=-,从0I 的⼏个近似值出发,计算20I ;解:易得:0I =ln6-ln5=0.1823, 程序为:I=0.182; for n=1:20I=(-5)*I+1/n; end I输出结果为:20I = -3.0666e+010 (2)粗糙估计20I ,⽤nI I n n 515111+-=--,计算0I ;因为 0095.056 0079.01020201020≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2120=+=I 程序为:I=0.0087; for n=1:20I=(-1/5)*I+1/(5*n); end I0I = 0.0083(3)分析结果的可靠性及产⽣此现象的原因(重点分析原因)。
⾸先分析两种递推式的误差;设第⼀递推式中开始时的误差为000I I E '-=,递推过程的舍⼊误差不计。
并记nn n I I E '-=,则有01)5(5E E E n n n -==-=-Λ。
因为=20E 20020)5(I E >>-,所此递推式不可靠。
⽽在第⼆种递推式中n n E E E )51(5110-==-=Λ,误差在缩⼩,所以此递推式是可靠的。
出现以上运⾏结果的主要原因是在构造递推式过程中,考虑误差是否得到控制,即算法是否数值稳定。
2.求⽅程0210=-+x e x的近似根,要求41105-+?<-k k x x ,并⽐较计算量。
(1)在[0,1]上⽤⼆分法;程序:a=0;b=1.0;while abs(b-a)>5*1e-4 c=(b+a)/2;if exp(c)+10*c-2>0 b=c; else a=c; end end c结果:c =0.0903(2)取初值00=x ,并⽤迭代1021x k e x -=+;程序:x=0; a=1;while abs(x-a)>5*1e-4 a=x;x=(2-exp(x))/10; end x结果:x =0.0905(3)加速迭代的结果;程序:x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;y=exp(x)+10*x-2; z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x); b=x; end x结果:x =0.0995(4)取初值00=x ,并⽤⽜顿迭代法;程序:x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x; end x结果: x =0.0905(5)分析绝对误差。


数值计算方法上机实验考试答案1. 小型火箭初始质量为900千克,其中包括600千克燃料。
火箭竖直向上发射时燃料以15千克/秒的速率燃烧掉,由此产生30000牛顿的恒定推力。
当燃料用尽时引擎关闭。
设火箭上升的整个过程中,空气阻力与速度平方成正比,比例系数为0.4(千克/米)。
重力加速度取9.8米/秒2.A. 建立火箭升空过程的数学模型(微分方程);B. 求引擎关闭瞬间火箭的高度、速度、加速度,及火箭到达最高点的时间和高度。
解:A . 建立模型:)(t x ——t 时刻的火箭高度;T =30000(牛顿)——火箭推力,当时间t >40秒时,T=0; m t m 150-=——火箭飞行过程中的质量,t >40秒时,300=m 千克0m =900(千克)——火箭初始质量; 1m =600(千克)——燃料质量;c =15(千克/秒)——燃料的燃烧速率; k =0.4(千克/米)——空气阻力系数; g =9.8(米/秒2)——重力加速度由能量守恒定律,可得到火箭飞行过程的方程:mg T t x k t x m -+'-=''2)]([)(这是一个初值问题,初始条件为 0)0(,0)0(='=x x设)(),(21t x x t x x '==,则问题化为求下列微分方程组的初值问题:⎪⎩⎪⎨⎧--+--='='g t m T x t m k x x x 151******** 0)0(,0)0(21==x xB . 关闭引擎时4015/600==t (秒),所求的是此时火箭的高度)40(1x ;速度)40(2x ;加速度)40()40(21x x '''或,及火箭到最高点的时间m t 和高度)(1m t x 。
具体的Matlab 程序如下: 首先建立微分方程的的m 文件:function y=huojian(t,x)k=0.4;g=9.8;m0=900;T=30000;m=m0-15*t;if t>40T=0;m=300;endy=[x(2),-(k/m)*x(2)^2+T/m-g]';主程序:%feixing.mk=0.4;g=9.8;m0=900;T=30000;x0=[0,0];ts=0:1:55;[t,x]=ode23('huojian',ts,x0);[t,x(:,1)]%------a=[t,x];x40=a(41,2) %燃料用尽时的高度v40=a(41,3) %燃料用尽时的速度a40=-(k/300)*v40^2+T/300-g %燃料用尽时的加速度%-------xmax=max(x(:,1)) %火箭到达最高点的高度subplot(2,1,1),plot(t,x(:,1)),title('altitude') subplot(2,1,2),plot(t,x(:,2)),title('speed')运行结果为:1.0e+003 *0 00.0010 0.01180.0020 0.04750.0030 0.10670.0040 0.18890.0050 0.29270.0060 0.41680.0070 0.55920.0080 0.71800.0090 0.89140.0100 1.07700.0380 7.80510.0390 8.06310.0400 8.32240.0410 8.54000.0420 8.70040.0430 8.82420.0440 8.92180.0450 8.99940.0460 9.06070.0470 9.10830.0480 9.14370.0490 9.16810.0500 9.18220.0510 9.18640.0520 9.18070.0530 9.16510.0540 9.13900.0550 9.1018x40 =8322.4v40 = 254.1728a40 = 4.0616xmax =9186.4关闭引擎时4015/600==t (秒),此时火箭的高度h=)40(1x =8322.4米,速度v=)40(2x =254.1728米/秒,加速度为a=)40(1x ''= 4.0616米/秒2,火箭到最高点的时间m t =51秒,高度)(1m t x =9186.4米。


上海电力学院数值分析上机实验报告题目:数值分析上机实验报告学生姓名:11111111111学号:111111*********专业:11112013年12月30日数值计算方法上机实习题1. 设⎰+=105dx xx I nn , (1) 由递推公式n I I n n 151+-=-,从0I 的几个近似值出发,计算20I ; (2) 粗糙估计20I ,用nI I n n 51511+-=-,计算0I ;(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
(1) 解答:n=0,0.1823)05ln()15ln()5(51515101010=+-+=++=+=+=⎰⎰⎰x d xdx x dx x x I nn这里可以用for 循环,while 循环,根据个人喜好与习惯:for 循环程序: While 循环程序: I=0.1823; I=0.1823; for n=1:20 i=1;I=(-5)*I+1/n; while i<21 End I=(-5)*I+1/i; I i=i+1; fprintf('I20=%f',I) end I = -2.0558e+009 >> II20=-2055816073.851284>> I = -2.0558e+009 (2) 粗略估计I 20: Mathcad 计算结果: for 循环程序: While 循环程序: >> I=0.007998; I=0.007998; >> for n=1:20 n=1;I=(-0.2)*I+1/(5*n); while n<21End I=(-0.2)*I+1/(5*n); >> I n=n+1; I =0.0083 end >> II =0.0083(3) 算法误差分析:计算在递推过程中传递截断误差和舍入误差 第一种算法:(从1——>20)*000e I I=-***21111120115(5)5()555n n n n n n n n n n e I I I I I I e e e n n------=-=-+--+=-===1x x 205x +⎛⎜⎜⎜⎠d 7.998103-⨯=误差放大了5n 倍,算法稳定性很不好; 第二种算法:(从20——>1)*n n ne I I =-***111111111()()555555n n n n n n nn e I I I I I I e n n ---=-=-+--+=-=0111...()55nne e e ===误差在逐步缩小,算法趋近稳定,收敛。
实习题1 1用两种不容的顺序计算644834.1100012nn,分析误差的变化 (1)顺序计算 源代码: #include #include void main() { double sum=0; int n=1; while(1) { sum=sum+(1/pow(n,2)); if(n%1000==0)printf("sun[%d]=%-30f",n,sum); if(n>=10000)break; n++; } printf("sum[%d]=%f\n",n,sum); }
结果:
(2)逆序计算 源代码: #include #include void main() { double sum=0; int n=10000; while(1) { sum=sum+(1/pow(n,2)); if(n%1000==0) printf("sum[%d]=%-30f",n,sum); if(n<=1)break; n--; } printf("sum[%d]=%f\n",n,sum); }
结果:
2已知连分数 ))//(.../(322101nnbaabababf
利用下面的方法计算f: 011)0,...,2,1(,dfnnidabdbdiiiinn
写一个程序,读入n,nnba,,计算并打印f 源代码: #include #include void main() { int i=0,n; float a[1024],b[1024],d[1024]; printf("please input n,n="); scanf("%d",&n); printf("\nplease input a[1] to a[n]:\n"); for(i=1;i<=n;i++) { printf("a[%d]=",i); scanf("%f",&a[i]);



1.设I n 1 x ndx ,0 5 x( 1)由递推公式 I n 5I n 11,从 I 0的几个近似值出发,计算I 20;n解:易得: I 0 ln6-ln5=0.1823, 程序为:I=0.182;for n=1:20I=(-5)*I+1/n;endI输出结果为: I 20= -3.0666e+010( 2)粗糙估计 I 20,用 I n 1 1I n 1 1 ,计算 I 0;5 5n0.0079 1 x 20 1 x 200.0095因为dx I 20dx 6 5所以取 I 20 1(0.0079 0.0095) 0.0087 2程序为: I=0.0087;for n=1:20I=(-1/5)*I+1/(5*n);endII 0= 0.0083( 3)分析结果的可靠性及产生此现象的原因(重点分析原因 )。
首先分析两种递推式的误差;设第一递推式中开始时的误差为E0 I 0 I 0,递推过程的舍入误差不计。
并记 E n I n I n,则有 E n 5E n 1 ( 5) n E0。
因为 E20( 5) 20 E0 I 20,所此递推式不可靠。
而在第二种递推式中E0 1E1 (1)n E n,误差在缩小,5 5所以此递推式是可靠的。
出现以上运行结果的主要原因是在构造递推式过程中,考虑误差是否得到控制,即算法是否数值稳定。
2.求方程e x10x 2 0 的近似根,要求x k 1x k 5 10 4,并比较计算量。
(1)在 [0, 1]上用二分法;程序: a=0;b=1.0;while abs(b-a)>5*1e-4c=(b+a)/2;if exp(c)+10*c-2>0b=c;else a=c;endendc结果: c =0.0903( 2)取初值x0 0,并用迭代 x k 1 2 e x ;10程序: x=0;a=1;while abs(x-a)>5*1e-4a=x;x=(2-exp(x))/10;endx结果: x =0.0905(3)加速迭代的结果;程序: x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;y=exp(x)+10*x-2;z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x);b=x;endx结果: x =0.0995( 4)取初值x00 ,并用牛顿迭代法;程序: x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x;end x 结果: x =0.0905( 5) 分析绝对误差。

高等代数机算与应用作业题学号:姓名:成绩:一、机算题1.利用函数rand和函数round构造一个5×5的随机正整数矩阵A和B。
>> a=round(rand(5))a =0 0 1 1 11 1 0 1 01 0 1 0 10 1 1 0 00 0 1 0 1>> b=round(rand(5))b =0 0 0 0 00 1 1 0 10 1 1 1 01 1 0 1 00 1 1 1 0(1)计算A+B,A-B和6A>> a+bans =0 0 1 1 11 2 1 1 11 12 1 11 2 1 1 00 1 2 1 1>> a-bans =0 0 1 1 11 0 -1 1 -1 1 -1 0 -1 1 -1 0 1 -1 0 0 -1 0 -1 1 >> 6*a ans =0 0 6 6 6 6 6 0 6 0 6 0 6 0 6 0 6 6 0 0 0 0 6 0 6 (2)计算()TAB ,TTB A 和()100AB>> (a*b)' ans =1 1 0 0 0 32 2 2 2 2 1 2 2 23 1 2 1 2 0 1 0 1 0 >> b'*a' ans =1 1 0 0 0 32 2 2 2 2 1 2 2 23 1 2 1 2 0 1 0 1 0 >> (a*b)^100 ans = 1.0e+078 *1.4732 7.6495 6.1764 5.52252.1271 1.0117 5.2535 4.24183.7927 1.4608 0.92294.7921 3.8692 3.4596 1.3325 0.9229 4.7921 3.8692 3.4596 1.3325 0.9229 4.7921 3.8692 3.4596 1.3325 (3)计算行列式A ,B 和AB >> det(a) ans =1 >> det(b) ans = 0 >> det(a*b) ans = 0(4)若矩阵A 和B 可逆,计算1A -和1B - >> inv(a) ans =0 0 1.0000 0 -1.0000 -1.0000 1.0000 -1.0000 0.0000 2.0000 1.0000 -1.0000 1.0000 1.0000 -2.0000 1.0000 0.0000 -0.0000 -0.0000 -1.0000 -1.0000 1.0000 -1.0000 -1.0000 3.0000 b 不存在逆矩阵(5)计算矩阵A 和矩阵B 的秩。
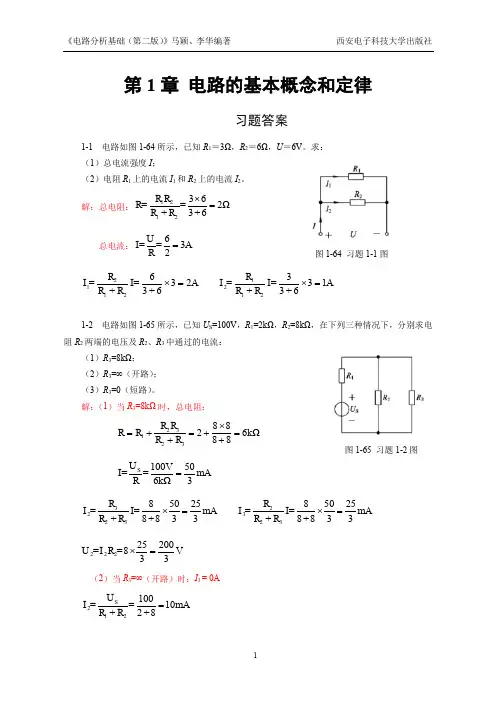
第1章 电路的基本概念和定律习题答案1-1 电路如图1-64所示,已知R 1=3Ω,R 2=6Ω,U =6V 。
求: (1)总电流强度I ;(2)电阻R 1上的电流I 1和R 2上的电流I 2。
解:总电阻:Ω26+36×3+2121==R R R R R=总电流:A 326==R U I=A 236+36+2121=⨯I=R R R =I A 136+33+2112=⨯I=R R R =I1-2 电路如图1-65所示,已知U S =100V ,R 1=2kΩ,R 2=8kΩ,在下列三种情况下,分别求电阻R 2两端的电压及R 2、R 3中通过的电流:(1)R 3=8kΩ; (2)R 3=∞(开路); (3)R 3=0(短路)。
解:(1)当R 3=8kΩ时,总电阻:k Ω68888232321=+⨯+=++=R R R R R RmA 350k Ω6V 100S ==R U I=mA 3253508+88+3232=⨯I=R R R =I mA 3253508+88+3223=⨯I=R R R =IV 32003258222=⨯=R =I U (2)当R 3=∞(开路)时:I 3 = 0A mA108+2100+21S 2==R R U =I图1-64 习题1-1图图1-65 习题1-2图V 80108222=⨯=R =I U(3)当R 3=0(短路)时:I 2 = 0A ,U 2 = 0V ;mA 50k Ω2V1001S 3==R U =I1-3 图1-66所示的各元件均为负载(消耗电能),其电压、电流的参考方向如图中所示。
已知各元件端电压的绝对值为5V ,通过的电流绝对值为4A 。
(1)若电压参考方向与真实方向相同,判断电流的正负; (2)若电流的参考方向与真实方向相同,判断电压的正负。
(a) (b) (c) (d)图1-66 习题1-3图解:(1)若电压参考方向与真实方向相同时: 图(a ):电压与电流参考方向关联,电流为正I =4A ; 图(b ):电压与电流参考方向非关联,电流为负I =-4A ; 图(c ):电压与电流参考方向关联,电流为正I =4A ; 图(d ):电压与电流参考方向非关联,电流为负I =-4A 。
实习题11用两种不容的顺序计算644834.1100012≈∑=-n n,分析误差的变化〔1〕顺序计算 源代码:#include<stdio.h> #include<math.h> void main() { double sum=0; int n=1; while(1) { sum=sum+(1/pow(n,2)); if(n%1000==0)printf("sun[%d]=%-30f",n,sum); if(n>=10000)break; n++; } printf("sum[%d]=%f\n",n,sum); }结果:〔2〕逆序计算 源代码:#include<stdio.h> #include<math.h> void main() { double sum=0; int n=10000; while(1) { sum=sum+(1/pow(n,2));if(n%1000==0) printf("sum[%d]=%-30f",n,sum); if(n<=1)break; n--; } printf("sum[%d]=%f\n",n,sum); }结果:2连分数))//(.../(322101n n b a a b a b a b f ++++=利用下面的方法计算f:11)0,...,2,1(,d f n n i d a b d b d i i i i n n =--=+==++写一个程序,读入n,n n b a ,,计算并打印f 源代码:#include<stdio.h> #include<math.h> void main() { int i=0,n; float a[1024],b[1024],d[1024]; printf("please input n,n="); scanf("%d",&n); printf("\nplease input a[1] to a[n]:\n"); for(i=1;i<=n;i++) { printf("a[%d]=",i); scanf("%f",&a[i]);} printf("\nplease input b[0] to b[n]:\n"); for(i=0;i<=n;i++) { printf("b[%d]=",i); scanf("%f",&b[i]); } d[n]=b[n]; for(i=n-1;i>=0;i--) d[i]=b[i]+a[i+1]/d[i+1]; printf("\nf=%f\n",d[0]); }结果:3给出一个有效的算法和一个无效的算法计算积分⎰=+=10)10,...1,0(14n dx x x y n n 源代码:#include<stdio.h> #include<math.h> main() { double y_0=(1/4.0)*log(5),y_1; double y_2=(1.0/55.0+1.0/11.0)/2,y_3; int n=1,m=10; printf("有效算法输出结果:\n"); printf("y[0]=%-20f",y_0);while(1) { y_1=1.0/(4*n)+y_0/(-4.0); printf("y[%d]=%-20f",n,y_1); if(n>=10) break; y_0=y_1; n++; if(n%3==0) printf("\n"); } printf("\n 无效算法的输出结果:\n"); printf("y[10]=%-20f",y_2); while(1) { y_3=1.0/n-4.0*y_2; printf("y[%d]=%-20f",m-1,y_3); if(m<=1) break; y_2=y_3; m--; if(m%2==0) printf("\n"); } }结果:4设∑=-=Nj N j S 2211,其准确值为)11123(21+--N N (1)编制按从小到大顺序计算N S 的程序 (2)编制按从小到达的顺序计算N S 的程序(3)按两种顺序分别计算30000100001000,,S S S ,并指出有效位数源代码:#include<stdio.h> main() { int N; double SN[30000]; SN[30000]=(3.0/2.0-1.0/30000.0-1/30001.0)/2.0; for(N=30000;N>=2;N--) SN[N-1]=SN[N]-1.0/(N*N-1); printf("从大到小顺序计算:\nSN[1000]=%f\nSN[10000]=%f\nSN[30000]=%f\n",SN[1000],SN[10000],SN[30000]); SN[2]=(3.0/2-1.0/2.0-1/3.0)/2.0; for(N=3;N<=30000;N++) SN[N]=SN[N-1]+1.0/(N*N-1); printf("从小到大顺序计算:\nSN[1000]=%f\nSN[10000]=%f\nSN[30000]=%f\n",SN[1000],SN[10000],SN[30000]); }结果:实习题21.用牛顿法求以下方程的根2=-x e x01=-x xe 02lg =-+x x源代码:#include <stdio.h> #include <math.h>typedef float (*p)(float ); float ff1(float x) { return x*x-exp(x); }float ff2(float x) { return x*exp(x)-1; }float ff3(float x) { return log(x)+x-2; }float answer(float(*p)(float)) { int k=2; float m=1,n=-1,x2,a,b,c; if (p==ff3)n=2; printf("x[0] = %.4f, x[1] = %.4f, ",m,n); while (1) { if (fabs(m-n)<1e-4) break; a=p(n)*(n-m); b=p(n)-p(m); c=a/b; x2=n-c; m = n; n = x2; printf("x[%d] = %.4f, ",k,x2); k++; if (k%3==0) printf("\n"); }if (k%3!=0) printf("\n");printf("iteration times: %d, roots: %.4f\n ",k-2,n);return 0;}main(){printf("x*x-exp(x),\n");answer(ff1);printf("x*exp(x)-1,\n");answer(ff2);printf("lg(x)+x-2,\n");answer(ff3);return 0;}结果:2.编写一个割线法的程序,求解上述各方程源代码:#include<stdio.h>#include<math.h>float gexian(float,float);float f(float);main(){int i,j;float x1=2.2;float x2=2,x3;scanf("%d",&i);if(i==1)printf("%f",x1); else if(i==2) printf("%f",x2); else { for(j=3;j<=i;j++) { x3=gexian(x1,x2); x1=x2; x2=x3; } printf("%f",gexian(x1,x2)); } }float f(float x) { return (x*x-exp(x)); }float gexian(float x1,float x2) { return (x2-(f(x2)/(f(x2)-f(x1)))*(x2-x1)); }结果:实习题31用列主元消去法解以下方程组;⎪⎪⎩⎪⎪⎨⎧=++=-++--=+--=--+43443233312)1(421432143214321x x x x x x x x x x x x x x x ⎪⎪⎩⎪⎪⎨⎧=++--=++-=-+--=-+-4341220332282)2(432132143214321x x x x x x x x x x x x x x x 源程序:#include<stdio.h>#include<math.h>void ColPivot(float*,int,float[]);void ColPivot(float*c,int n,float x[]){int i,j,t,k;float p;for(i=0;i<=n-2;i++){k=i;for(j=i+1;j<=n-1;j++)if(fabs(*(c+j*(n+1)+i))>(fabs(*(c+k*(n+1)+i))))k=j;if(k!=i)for(j=i;j<=n;j++){p=*(c+i*(n+1)+j);*(c+i*(n+1)+j)=*(c+k*(n+1)+j);*(c+k*(n+1)+j)=p;}for(j=i+1;j<=n-1;j++){p=(*(c+j*(n+1)+i))/(*(c+i*(n+1)+i));for(t=i;t<=n;t++)*(c+j*(n+1)+t)-=p*(*(c+i*(n+1)+t));}}for(i=n-1;i>=0;i--){for(j=n-1;j>=i+1;j--)(*(c+i*(n+1)+n))-=x[j]*(*(c+i*(n+1)+j));x[i]=*(c+i*(n+1)+n)/(*(c+i*(n+1)+i));}}void main(){int i;float x[4];float c[4][5]={1,1,0,3,4,2,1,-1,1,1,3,-1,-1,3,-3,-1,2,3,-1,4};ColPivot(c[0],4,x);for(i=0;i<=3;i++)printf("x[%d]=%f\n",i,x[i]);}结果:第〔1〕题第〔2〕题2、源代码:#include<stdio.h>void main(){float x[4];int i;float a[4][5]={48,-24,0,-12,4,-24,24,12,12,4,0,6,20,2,-2,-6,6,2,16,-2};void DirectLU(float*,int,float[]);DirectLU(a[0],4,x);for(i=0;i<=3;i++)printf("x[%d]=%f\n",i,x[i]);}void DirectLU(float*u,int n,float x[]){int i,r,k;for(r=0;r<=n-1;r++){for(i=r;r<=n;i++)for(k=0;k<=r-1;k++)*(u+r*(n+1)+i)-=*(u+r*(n+1)+k)*(*(u+k*(n+1)+i));for(i=r+1;i<=n-1;i++){for(k=0;k<=r-1;k++)*(u+i*(n+1)+r)-=*(u+i*(n+1)+k)*(*(u+k*(n+1)+r));*(u+i*(n+1)+r)/=*(u+r*(n+1)+r);}}for(i=n-1;i>=0;i--){for(r=n-1;r>=i+1;r--)*(u+i*(n+1)+n)-=*(u+i*(n+1)+r)*x[r];x[i]=*(u+i*(n+1)+n)/(*(u+i*(n+1)+i));}}实习题41、源代码:#include<stdio.h>float Lagrange(float x[],float y[],float xx,int n) //n为〔n+1〕次插值;{int i,j;float *a,yy=0;a=new float[n];for(i=0;i<=n-1;i++){a[i]=y[i];for(j=0;j<=n-1;j++)if(j!=i)a[i]*=(xx-x[j])/(x[i]-x[j]);yy+=a[i];}delete a;return yy;}void main(){float x[5]={-3.0,-1.0,1.0,2.0,3.0};float y[5]={1.0,1.5,2.0,2.0,1.0};float xx1=-2,xx2=0,xx3=2.75,yy1,yy2,yy3;yy1=Lagrange(x,y,xx1,3);yy2=Lagrange(x,y,xx2,3);yy3=Lagrange(x,y,xx3,3);printf("x1=%-20f,y1=%f\n",xx1,yy1);printf("x2=%-20f,y2=%f\n",xx2,yy2);printf("x3=%-20f,y3=%f\n",xx3,yy3);}结果:2、源代码:#include<stdio.h>float Lagrange(float x[],float y[],float xx,int n) //n为〔n+1〕次插值;{int i,j;float *a,yy=0;a=new float[n];for(i=0;i<=n-1;i++){a[i]=y[i];for(j=0;j<=n-1;j++)if(j!=i)a[i]*=(xx-x[j])/(x[i]-x[j]);yy+=a[i];}delete a;return yy;}void main(){float x[6]={0.30,0.42,0.50,0.58,0.66,0.72};float y[6]={1.04403,1.08462,1.11803,1.15603,1.19817,1.23223};float xx1=0.46,xx2=0.55,xx3=0.60,yy1,yy2,yy3;yy1=Lagrange(x,y,xx1,6);yy2=Lagrange(x,y,xx2,6);yy3=Lagrange(x,y,xx3,6);printf("x1=%-20f,y1=%f\n",xx1,yy1);printf("x2=%-20f,y2=%f\n",xx2,yy2);printf("x3=%-20f,y3=%f\n",xx3,yy3);}结果:源代码:#include<stdio.h>#define N 3void Difference(float y[],float f[4][4],int n){int k,i;f[0][0]=y[0];f[1][0]=y[1];f[2][0]=y[2];f[3][0]=y[3];for(k=1;k<=n;k++)for(i=0;i<=(N-k);i++)f[i][k]=f[i+1][k-1]-f[i][k-1];return;}void main(){int i,k=1;float a,b=1,m=21.4,t=1.4,f[4][4]={0};float x[5]={20,21,22,23,24};float y[5]={1.30103,1.32222,1.34242,1.36173,1.38021};Difference(y,f,N);a=f[0][0];for(i=1;i<=N;i++){k=k*i;b=b*(t-i+1);a=a+b*f[0][i]/k;}printf("x(k)\n");for (i=0;i<=4;i++)printf( "%-20f",x[i]);printf("\ny(k)\n");for (i=0;i<=4;i++)printf("%-20f",y[i]);for(k=1;k<=3;k++){printf("\nF(%d)\n ",k);for(i=0;i<=(3-k);i++){printf("%-20f",f[i][k]);}}printf ("\n");printf("f(%f)=%-20f",m,a);printf ("\n");结果:实习题52、源代码:#include<stdio.h>#include<math.h>void main(){int i,n;float a[2];float x[15]={1,1.5,2,2.5,3,3.5,4,4.5,5,5.5,6,6.5,7,7.5,8},z[15];floaty[15]={33.4,79.50,122.65,159.05,189.15,214.15,238.65,252.50,267.55,280.50,296.65,301.40,310. 40,318.15,325.15};for(n=0;n<=14;n++) //增加了数组z;{z[n]=log(y[n]/x[n]);}void Approx(float[],float[],int,int,float[]);Approx(x,z,15,1,a); //变成一次拟合;//for(i=0;i<=1;i++)//printf("a[%d]=%f\n",i,a[i]);printf("a=exp(a[0])=%f\n",exp(a[0]));printf("b=-a[1]=%f\n",-a[1]); }void Approx(float x[],float y[],int m,int n,float a[]){int i,j,t;float *c=new float[(n+1)*(n+2)];float power(int,float);void ColPivot(float *,int,float[]);for(i=0;i<=n;i++){for(j=0;j<=n;j++){*(c+i*(n+2)+j)=0;for(t=0;t<=m-1;t++)*(c+i*(n+2)+j)+=power(i+j,x[t]);}*(c+i*(n+2)+n+1)=0;for(j=0;j<=m-1;j++)*(c+i*(n+2)+n+1)+=y[j]*power(i,x[j]);}ColPivot(c,n+1,a);delete c;}void ColPivot(float *c,int n,float x[]){int i,j,t,k;float p;for(i=0;i<=n-2;i++){k=i;for(j=i+1;j<=n-1;j++)if(fabs(*(c+j*(n+1)+i))>(fabs(*(c+k*(n+1)+i))))k=j;if(k!=i)for(j=i;j<=n;j++){p=*(c+i*(n+1)+j);*(c+i*(n+1)+j)=*(c+k*(n+1)+j);*(c+k*(n+1)+j)=p;}for(j=i+1;j<=n-1;j++){p=(*(c+j*(n+1)+i))/(*(c+i*(n+1)+i));for(t=i;t<=n;t++)*(c+j*(n+1)+t)-=p*(*(c+i*(n+1)+t));}}for(i=n-1;i>=0;i--){for(j=n-1;j>=i+1;j--)(*(c+i*(n+1)+n))-=x[j]*(*(c+i*(n+1)+j));x[i]=*(c+i*(n+1)+n)/(*(c+i*(n+1)+i));}float power(int i,float v){float a=1;while(i--)a*=v;return a;}结果:实习题61、源代码:〔1〕#include<stdio.h>#include<math.h>float Cotes(float(*f)(float),float a,float b,int n){int k;float c,c1=0,c2,c3,c4;float h=(b-a)/n;c2=(*f)(a+h/4);c3=(*f)(a+h/2);c4=(*f)(a+3*h/4);for(k=1;k<=n-1;k++){c1+=(*f)(a+k*h);c2+=(*f)(a+k*h+h/4);c3+=(*f)(a+k*h+h/2);c4+=(*f)(a+k*h+3*h/4);}c=h/90*(7*((*f)(a)+(*f)(b))+14*c1+32*c2+12*c3+32*c4);return c;}float f(float x){return 1/sqrt(1+x*x*x);}void main()int i,n=4;float c;for(i=0;i<=4;i++){c=Cotes(f,0,1,n);printf("C(%d)=%f\n",n,c);n*=2;}}〔2〕#include<stdio.h>#include<math.h>float Cotes(float(*f)(float),float a,float b,int n){int k;float c,c1=0,c2,c3,c4;float h=(b-a)/n;c2=(*f)(a+h/4);c3=(*f)(a+h/2);c4=(*f)(a+3*h/4);for(k=1;k<=n-1;k++){c1+=(*f)(a+k*h);c2+=(*f)(a+k*h+h/4);c3+=(*f)(a+k*h+h/2);c4+=(*f)(a+k*h+3*h/4);}c=h/90*(7*((*f)(a)+(*f)(b))+14*c1+32*c2+12*c3+32*c4);return c;}float f(float x){ // return 1/sqrt(1+x*x*x);if (x==0)return 1;else return sin(x)/x;}void main(){int i,n=4;float c;for(i=0;i<=4;i++){// c=Cotes(f,0,1,n);c=Cotes(f,0,5,n);printf("C(%d)=%f\n",n,c);n*=2;}}结果:〔1〕〔2〕实习题7 一、改良欧拉法1、#include<stdio.h>#include<iostream>double Adams (double (*f)(double x, double y),double x0,double y0,double h,int N) {for(int n=0; n<N; ++n) {double x1=x0+h;double yp=y0+h*f(x0,y0);double y1=y0+h*f(x1,yp);y1=(yp+y1)/2.0;printf("ty=%f\n",y1);x0=x1;y0=y1;}}int main(void){double f(double x, double y); double x0=0,y0=0;double x,y,step;long i;step=0.1;Adams(f,x0,y0,0.1,10);}double f(double x, double y) {double r;r=x*x+y*y;return(r);}2、int main(void){double f(double x, double y); double x0=0,y0=0;double x,y,step;long i;step=0.1;Adams(f,x0,y0,0.1,10);}double f(double x, double y) {double r;r=1/(1+y*y);return(r);}3、int main(void){double f(double x, double y); double x0=0,y0=1;double x,y,step;long i;step=0.1;Adams(f,x0,y0,0.1,10);}double f(double x, double y) {double r;r=y-2*x/y;return(r);}四阶龙格库塔法1、#include<iostream>#include<stdio.h>using namespace std;//f为函数的入口地址,x0、y0为初值,xn为所求点,step为计算次数double Runge_Kuta( double (*f)(double x, double y), double x0, double y0, double xn, long step ) {double k1,k2,k3,k4,result;double h=(xn-x0)/step;if(step<=0)return(y0);if(step==1){k1=f(x0,y0);k2=f(x0+h/2, y0+h*k1/2);k3=f(x0+h/2, y0+h*k2/2);k4=f(x0+h, y0+h*k3);result=y0+h*(k1+2*k2+2*k3+k4)/6;}else{double x1,y1;x1=xn-h;y1=Runge_Kuta(f, x0, y0, xn-h,step-1);k1=f(x1,y1);k2=f(x1+h/2, y1+h*k1/2);k3=f(x1+h/2, y1+h*k2/2);k4=f(x1+h, y1+h*k3);result=y1+h*(k1+2*k2+2*k3+k4)/6;}printf("%lg\n",result);return(result);}int main(void){double f(double x, double y);double x0=0,y0=0,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl; //}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=x*x+y*y;return(r);}2、int main(void){double f(double x, double y);double x0=0,y0=0,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl; //}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=1/〔1+y*y〕;return(r);}3、int main(void){double f(double x, double y);double x0=0,y0=0,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl; //}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=1/〔1+y*y〕;return(r);}二、int main(void){double f(double x, double y);double x0=0,y0=1,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl;//}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=y-2*x/y;return(r);}三、1、void Runge_Kutta(float(*f)(float x,float y),float a,float b,float y0,int N,float yy[]) {float x=a,y=y0,K1,K2,K3,K4;float h=(b-a)/N;int i;for(i=1;i<=3;i++){K1=(*f)(x,y);K2=(*f)(x+h/2,y+h*K1/2);K3=(*f)(x+h/2,y+h*K2/2);K4=(*f)(x+h/2,y+h*K3);y=y+h*(K1+2*K2+2*K2+2*K3+K4)/6;x=a+i*h;yy[i-1]=y;}}void Adams (float a,float b,int N,float(*f)(float x,float y),float y0){int i;float y1,y2,y,yp,yc,yy[3],h,x;printf("x[0]=%f\ty[0]=%f\n",a,y0);Runge_Kutta(f,a,b,y0,N,yy);y1=yy[0];y2=yy[1];y=yy[2];h=(b-a)/N;for(i=1;i<=3;i++)printf("x[%d]=%f\ty[%d]=%f\n",i,a+i*h,i,yy[i-1]);for(i=3;i<N;i++){x=a+i*h;yp=y+h*(55*f(x,y)-59*f(x-h,y2)+37*f(x-2*h,y1)-9*f(x-3*h,y0))/24;yc=y+h*(9*(*f)(x+h,yp)+19*(*f)(x,y)-5*(*f)(x-h,y2)+(*f)(x-2*h,y1))/24;printf("x[%d]=%f\ty[%d]=%f\n",i+1,x+h,i+1,yc);y0=y1;y1=y2;y2=y;y=yc;}}float f(float x,float y){return y*y;void Runge_Kutta(float(*f)(float x,float y),float a,float,float b,float y0,int N,float yy[]); void Adams (float a,float b,int N,float(*f)(float x,float y),float y0);float f(float x,float y);int main (void){float a=0,b=1,y0=1;int N=10;Adams(a,b,N,f,y0);}2、#include<stdio.h>void Runge_Kutta(float(*f)(float x,float y),float a,float b,float y0,int N,float yy[]) {float x=a,y=y0,K1,K2,K3,K4;float h=(b-a)/N;int i;for(i=1;i<=3;i++){K1=(*f)(x,y);K2=(*f)(x+h/2,y+h*K1/2);K3=(*f)(x+h/2,y+h*K2/2);K4=(*f)(x+h/2,y+h*K3);y=y+h*(K1+2*K2+2*K2+2*K3+K4)/6;x=a+i*h;yy[i-1]=y;}}void Adams (float a,float b,int N,float(*f)(float x,float y),float y0)int i;float y1,y2,y,yp,yc,yy[3],h,x;printf("x[0]=%f\ty[0]=%f\n",a,y0);Runge_Kutta(f,a,b,y0,N,yy);y1=yy[0];y2=yy[1];y=yy[2];h=(b-a)/N;for(i=1;i<=3;i++)printf("x[%d]=%f\ty[%d]=%f\n",i,a+i*h,i,yy[i-1]);for(i=3;i<N;i++){x=a+i*h;yp=y+h*(55*f(x,y)-59*f(x-h,y2)+37*f(x-2*h,y1)-9*f(x-3*h,y0))/24;yc=y+h*(9*(*f)(x+h,yp)+19*(*f)(x,y)-5*(*f)(x-h,y2)+(*f)(x-2*h,y1))/24;printf("x[%d]=%f\ty[%d]=%f\n",i+1,x+h,i+1,yc);y0=y1;y1=y2;y2=y;y=yc;}}float f(float x,float y){return 0.1*(x*x*x+y*y);}void Runge_Kutta(float(*f)(float x,float y),float a,float,float b,float y0,int N,float yy[]); void Adams (float a,float b,int N,float(*f)(float x,float y),float y0);float f(float x,float y);int main (void){float a=0,b=1,y0=1;int N=10;Adams(a,b,N,f,y0);}。
第一章 传感与检测技术的理论基础1.什么是测量值的绝对误差、相对误差、引用误差? 答:某量值的测得值和真值之差称为绝对误差。
相对误差有实际相对误差和标称相对误差两种表示方法。
实际相对误差是绝对误差与被测量的真值之比;标称相对误差是绝对误差与测得值之比。
引用误差是仪表中通用的一种误差表示方法,也用相对误差表示,它是相对于仪表满量程的一种误差。
引用误差是绝对误差(在仪表中指的是某一刻度点的示值误差)与仪表的量程之比。
2.什么是测量误差?测量误差有几种表示方法?它们通常应用在什么场合? 答:测量误差是测得值与被测量的真值之差。
测量误差可用绝对误差和相对误差表示,引用误差也是相对误差的一种表示方法。
在实际测量中,有时要用到修正值,而修正值是与绝对误差大小相等符号相反的值。
在计算相对误差时也必须知道绝对误差的大小才能计算。
采用绝对误差难以评定测量精度的高低,而采用相对误差比较客观地反映测量精度。
引用误差是仪表中应用的一种相对误差,仪表的精度是用引用误差表示的。
3.用测量范围为-50~+150kPa 的压力传感器测量140kPa 压力时,传感器测得示值为142kPa ,求该示值的绝对误差、实际相对误差、标称相对误差和引用误差。
解:绝对误差 2140142=-=∆kPa实际相对误差%43.1%100140140142=⨯-=δ 标称相对误差%41.1%100142140142=⨯-=δ 引用误差%1%10050150140142=⨯---=)(γ4.什么是随机误差?随机误差产生的原因是什么?如何减小随机误差对测量结果的影响?答:在同一测量条件下,多次测量同一被测量时,其绝对值和符号以不可预定方式变化着的误差称为随机误差。
随机误差是由很多不便掌握或暂时未能掌握的微小因素(测量装置方面的因素、环境方面的因素、人员方面的因素),如电磁场的微变,零件的摩擦、间隙,热起伏,空气扰动,气压及湿度的变化,测量人员感觉器官的生理变化等,对测量值的综合影响所造成的。
西安电子科技大学出版社《计算方法》任传祥等编著第九章计算方法上机参考答案实验一,算法一#include <stdio.h>#include <math.h>double I0=log(6)/log(5),I1;int n=1;main (){while(1){I1=1.0/(n)-I0*5.0;printf("%d %lf\n", n,I1);if(n>=20)break;elseI0=I1;n++;}}实验一,算法二#include <stdio.h>#include <math.h>double I0=(1/105.0+1/126.0)/2,I1;int n=20;main (){printf("%d %lf\n", n,I0);while(1){I1=1.0/(5.0*n)-I0/5.0;printf("%d %lf\n", n-1,I1);if(n<2)break;elseI0=I1;n--;}}实验二,二分法#include <stdio.h>#include <math.h>#define esp 1e-3double f(double x);main (){double a=1,b=2,x;while(fabs(b-a)>esp){x=(a+b)/2;printf("x=%lf\n",x);if(f(x)==0)break;elseif(f(x)*f(a)<0)b=x;elsea=x;}}double f(double x){return pow(x,3)-x-1;}实验二,牛顿迭代法#include<stdio.h>#include<math.h>double f(double x);double f1(double x);#define esp 1e-3void main(){double x0 = 1.5, x1;x1 = x0 - f(x0) / f1(x0);printf("x=%lf\n", x1);x0 = x1;x1 = x0 - f(x0) / f1(x0);printf("x=%lf\n", x1);while (fabs(x1 - x0)>esp){x0 = x1;x1 = x0 - f(x0) / f1(x0);printf("x=%lf\n", x1);} }double f(double x){return pow(x, 3) - x - 1;} double f1(double x){return 3 * x*x - 1;}弦割法#include<stdio.h>#include<math.h>double f(double x);#define esp 1e-3void main(){double x0 = 1.5, x1=2.0,x2;do{ x2=x1 - (x1-x0)*f(x1) /(f(x1)-f(x0));x0=x1;x1=x2;printf("x=%lf\n", x1);}while (fabs(x1 - x0)>esp);{printf("x=%lf\n", x1);}}double f(double x){return pow(x, 3) - x - 1;}实验3#include <stdio.h>/*列主元高斯消去法*/#include <math.h>float x[3],temp,max;float A[3][4]={10,-2,-1,3,-2,10,-1,15,-1,-2,5,10},c[3][4]={10,-2,-1,3,-2,10,-1,15,-1,-2,5,10}; int n=3,i,k,j,m;void main(){for(i=0;i<n;i++){max=A[i][i];k=i;for(j=j+1;j<n;j++){{max=fabs(A[j][i]);k=j;}}if(k!=i){for(j=i+1;j<=n;j++){temp=A[i][j];A[i][j]=A[k][j];A[k][j]=temp;}}for(j=i+1;j<n;j++)for(m=i+1;m<=n;m++){c[j][m]=c[j][m]+(-c[j][i]/c[i][i])*c[i][m];}}for(i=n-1;i>=0;i--){temp=0.0;for(j=n-1;j>=i+1;j--)temp=temp+c[i][j]*x[j];x[i]=(c[i][n]-temp)/c[i][i];}printf("x[1]=%f\nx[2]=%f\nx[3]=%f\n",x[0],x[1],x[2]);实验四,拉格朗日插值#include<stdio.h>int n=5,i,j;double l,L=0,X=0.5;main(){double x[5]={0.4,0.55,0.65,0.8,0.9};doubley[5]={0.41075,0.57815,0.69675,0.88811,1.02652}; for(i=0;i<n;i++){l=y[i];for(j=0;j<n;j++){if(j!=i)l=l*(X-x[j])/(x[i]-x[j]); } L=L+l;}printf("%lf\n",L);return 0;} X=0.5 X=0.7 X=0.85牛顿插值法#include<stdio.h>#include<math.h>main(){double x[5]={0.4,0.55,0.65,0.8,0.9};doubley[5]={0.41075,0.57815,0.69675,0.88811,1.02652};int n=5,i,j;double z;printf("input z\n");scanf("%lf",&z);double a[5][5];for(i=0;i<5;i++)a[i][0]=y[i];for(i=1;i<5;i++)for(j=i;j<5;j++)a[j][i]=(a[j][i-1]-a[j-1][i-1])/(x[j]-x[j-i]);double N=a[0][0],temp=1.0;for(i=1;i<n;i++){temp=temp*(z-x[i-1]);N=N+a[i][i]*temp;}printf("N=%lf\n",N);return 0;}实验五曲线拟合#include <stdio.h>#include <math.h>float x[5]={1,2,3,4,5};float y[5]={7,11,17,27,40};float A[2][3],c[2][3];float z[2],temp,max;int i,j,k,m;int n=2;void main(){for(i=0;i<5;i++){c[0][0]=A[0][0]+=1;c[0][1]=A[0][1]+=x[i];c[0][2]=A[0][2]+=y[i];c[1][0]=A[1][0]+=x[i];c[1][1]=A[1][1]+=x[i]*x[i];c[1][2]=A[1][2]+=x[i]*y[i];}/* for(i=0;i<2;i++){printf(" %lf %lf %lf\n",A[i][0],A[i][1],A[i ][2]);}*/for(i=0;i<n;i++){max=A[i][i];k=i;for(j=j+1;j<n;j++){if(fabs(A[j][i])>max){max=fabs(A[j][i]);k=j;}} if(k!=i){for(j=i+1;j<=n;j++){temp=A[i][j];A[i][j]=A[k][j];A[k][j]=temp;}}for(j=i+1;j<n;j++)for(m=i+1;m<=n;m++){c[j][m]=c[j][m]+(-c[j][i]/c[i][i])*c[i][m];}}for(i=n-1;i>=0;i--){temp=0.0;for(j=n-1;j>=i+1;j--)temp=temp+c[i][j]*z[j];z[i]=(c[i][n]-temp)/c[i][i];}printf("a=%f\nxb=%f\n",z[0],z[1]); }实验六数值积分/*梯形*/#include<stdio.h>#include<math.h> double f(double x); main(){double x[10],y[10];double h,b=1,a=0,I;int n,i;printf("n\n");scanf("%d",&n);h=(b-a)/n;for(i=0;i<=n;i++){x[i]=a+(i*h);y[i]=f(x[i]);}I=f(a)+f(b);for(i=1;i<=n-1;i++){I=I+2*y[i];}I=(h/2)*I;printf("%lf",I);}double f(double x){double f;f=1.0/(1.0+(x*x));return(f);}/*辛普森*/#include<stdio.h>#include<math.h>double f(double x);main(){double x[30],y[30];double h,b=1,a=0,I;int n,i;printf("n\n");scanf("%d",&n);//点乘2扩展h=(b-a)/n;x[10]=1;y[10]=f(x[10]);for(i=0;i<n;i++){x[2*i]=a+(i*h);y[2*i]=f(x[2*i]);x[2*i+1]=a+(i+(1.0/2.0))*h;y[(2*i)+1]=f(x[(2*i)+1]);}I=f(a)+f(b);for(i=0;i<n;i++){I=I+4*y[(2*i)+1];}for(i=1;i<n;i++){I=I+2*y[2*i];}I=(h/6)*I;printf("%lf\n",I);}double f(double x){double f;f=1.0/(1.0+(x*x));return(f);}/*梯形*//*辛普森*/。