知道两点经纬度求两点距离公式

怎么用经纬度计算两地之间的距离？1、地球赤道上环绕地球一周走一圈共40075.04公里,而@一圈分成360°,而每1°(度)有60,每一度一秒在赤道上的长度计算如下：40075.04km/360°=111.31955km111.31955km/60=1.8553258km=1855.3m而每一分又有60秒,每一秒就代表1855.3m/60=30.92m任意两点距离计算公式为d＝111.12cos{1/[sinΦAsinΦB十cosΦAcosΦBcos(λB—λA)]}其中A点经度，纬度分别为λA和ΦA，B点的经度、纬度分别为λB和ΦB，d为距离。

2、分为3步计算：第1步分别将两点经纬度转换为三维直角坐标：假设地球球心为三维直角坐标系的原点，球心与赤道上0经度点的连线为X轴，球心与赤道上东经90度点的连线为Y轴，球心与北极点的连线为Z轴，则地面上点的直角坐标与其经纬度的关系为：x=R×cosα×cosβy=R×cosα×sinβz=R×sinαR为地球半径，约等于6400km；α为纬度，北纬取+，南纬取-；β为经度，东经取+，西经取-。

第2步根据直角坐标求两点间的直线距离（即弦长）：如果两点的直角坐标分别为(x1,y1,z1)和(x2,y2,z2)，则它们之间的直线距离为：L=[(x1-x2)^2+(y1-y2)^2+(z1-z2)^2]^0.5上式为三维勾股定理，L为直线距离。

第3步根据弦长求两点间的距离（即弧长）：由平面几何知识可知弧长与弦长的关系为：S=R×π×2[arc sin(0.5L/R)]/180上式中角的单位为度，1度＝π/180弧度，S为弧长。

3、1度的实际长度是111公里。

但纬线的距离会越考两端越小，他的距离就会变成111乘COS纬度数，经度不变。

4、南北方向算出两点纬度差,一度等于60海里,1分等于1海里,海里与公里换算关系1海里等于1.852公里。

根据两点经纬度计算距离这些经纬线是怎样定出来的呢？地球是在不停地绕地轴旋转（地轴是⼀根通过地球南北两极和地球中⼼的假想线），在地球中腰画⼀个与地轴垂直的⼤圆圈，使圈上的每⼀点都和南北两极的距离相等，这个圆圈就叫作“⾚道”。

在⾚道的南北两边，画出许多和⾚道平⾏的圆圈，就是“纬圈”；构成这些圆圈的线段，叫做纬线。

我们把⾚道定为纬度零度，向南向北各为90度，在⾚道以南的叫南纬，在⾚道以北的叫北纬。

北极就是北纬90度，南极就是南纬90度。

纬度的⾼低也标志着⽓候的冷热，如⾚道和低纬度地地区⽆冬，两极和⾼纬度地区⽆夏，中纬度地区四季分明。

其次，从北极点到南极点，可以画出许多南北⽅向的与地球⾚道垂直的⼤圆圈，这叫作“经圈”；构成这些圆圈的线段，就叫经线。

公元1884平⾯坐标图年，国际上规定以通过英国伦敦近郊的格林尼治天⽂台的经线作为计算经度的起点，即经度零度零分零秒，也称“本初⼦午线”。

在它东⾯的为东经，共180度；在它西⾯的为西经，共180度。

因为地球是圆的，所以东经180度和西经180度的经线是同⼀条经线。

各国公定180度经线为“国际⽇期变更线”。

为了避免同⼀地区使⽤两个不同的⽇期，国际⽇期变线在遇陆地时略有偏离。

每⼀经度和纬度还可以再细分为60分，每⼀分再分为60秒以及秒的⼩数。

利⽤经纬线，我们就可以确定地球上每⼀个地⽅的具体位置，并且把它在地图或地球仪上表⽰出来。

例如问北京的经纬度是多少？我们很容易从地图上查出来是东经116度24分，北纬39度54分。

在⼤海中航⾏的船只，只要把所在地的经度测出来，就可以确定船在海洋中的位置和前进⽅向。

纬度共有90度。

⾚道为0度，向两极排列，圈⼦越⼩，度数越⼤。

横线是纬度，竖线是经度。

当然可以计算，四元⼆次⽅程。

经度和纬度都是⼀种⾓度。

经度是个两⾯⾓，是两个经线平⾯的夹⾓。

因所有经线都是⼀样长，为了度量经度选取⼀个起点⾯，经1884年国际会议协商，决定以通过英国伦敦近郊、泰晤⼠河南岸的格林尼治皇家天⽂台（旧址）的⼀台主要⼦午仪⼗字丝的那条经线为起始经线，称为本初⼦午线。

已知经纬度，求两地的距离 - 附“两地距离计算器”2011-07-26 11:01式中：α和θ分别是两地的纬度，北纬记为正，南纬记为负；β是两地的经度差；r是地球半径。

忽略各地海拔高度差异，认为地球是理想的球面。

求出的L 是两地的直线距离（地球的一条弦长），l 是两地的球面距离（沿地球表面的弧长）。

线性文本：k=√((sin⁡θ-sin⁡α )^2+(cos⁡θ-cos⁡α cos⁡β )^2+(cos ⁡α sin⁡β )^2；L=rk，l=2r sin^(-1)⁡〖k/2〗公式注：arcsin得弧度值公式是我自己推导的。

式中的α和θ地位等价。

公式应用举例：求北京和悉尼之间的距离。

北京：39°54′57″N , 116°23′26″E悉尼：33°51′35.9″S , 151°12′40″E则：α=39°54′57″θ=－33°51′35.9″β=116°23′26″－151°12′40″=－34°49′14″代入公式中，查三角函数表，r取地球平均半径6371.004 千米，即可求得L = 8231.403 km l = 8949.214 km注意经度差的算法。

116°E和151°E相差151°-116°=35°，116°E和151°W相差360°-151°-116°=93°经度差35°或－35°或325°是等价的。

附两地距离计算器：此UI延续我造某的一贯风格。

比较易懂，操作说明我就不写了；如有问题可在本文下留言或联系我li.zaodie@。

下载地址：Distance.exe /self.aspx/z aodiesoft/distance.exe。

经纬度定位计算距离在现代科技的帮助下，我们可以轻松获取到地球上任意两点之间的经纬度坐标。

然而，仅有经纬度坐标是无法直观地知道这两点之间的距离的。

因此，我们需要借助数学和计算机编程的力量来计算经纬度定位之间的距离。

在计算经纬度定位之间的距离之前，我们需要先了解一些背景知识。

经度和纬度是地球表面上的两个基本地理坐标系统。

经度用来表示地球上的东西方向，从-180度到180度。

纬度则用来表示地球上的南北方向，从-90度到90度。

当我们获得了两个点的经纬度坐标后，如何计算它们之间的距离呢？有许多算法可以用来计算经纬度定位之间的距离，其中最常用的是Haversine公式。

Haversine公式基于球面三角学来计算地球上任意两点之间的最短距离。

这个公式的原理是将球面上的两点与球心连线看作是一个圆锥台，然后计算两个圆锥台的体积之差，最后得到的结果即为两点之间的距离。

下面是一个用Python编程语言实现Haversine公式的例子：```python import mathdef calculate_distance(lat1, lon1, lat2, lon2): R = 6371 # 地球半径，单位为千米lat1_rad = math.radians(lat1)lon1_rad = math.radians(lon1)lat2_rad = math.radians(lat2)lon2_rad = math.radians(lon2)delta_lon = lon2_rad - lon1_raddelta_lat = lat2_rad - lat1_rada = math.sin(delta_lat/2)**2 + math.cos(lat1_rad) * math.cos(lat2_rad)* math.sin(delta_lon/2)**2c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a))distance = R * creturn distance示例坐标点lat1 = 39.9042 lon1 = 116.4074 lat2 = 31.2304 lon2 = 121.4737distance = calculate_distance(lat1, lon1, lat2, lon2) print(。

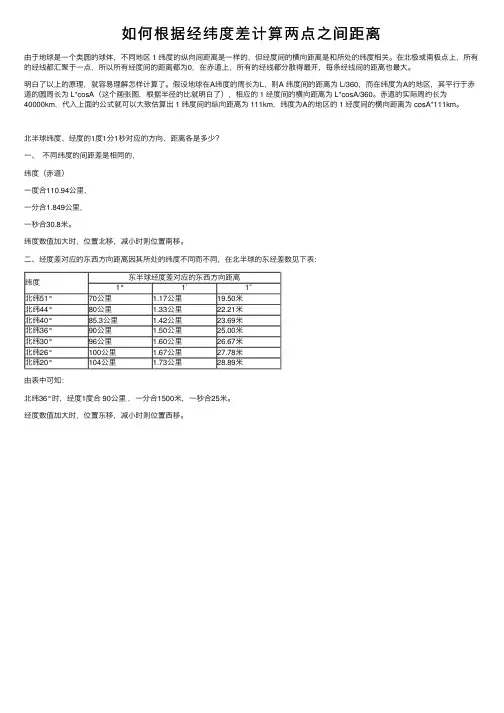
如何根据经纬度差计算两点之间距离由于地球是⼀个类圆的球体，不同地区 1 纬度的纵向间距离是⼀样的，但经度间的横向距离是和所处的纬度相关。

在北极或南极点上，所有的经线都汇聚于⼀点，所以所有经度间的距离都为0，在⾚道上，所有的经线都分散得最开，每条经线间的距离也最⼤。

明⽩了以上的原理，就容易理解怎样计算了。

假设地球在A纬度的周长为L，则A 纬度间的距离为 L/360，⽽在纬度为A的地区，其平⾏于⾚道的圆周长为 L*cosA（这个画张图，根据半径的⽐就明⽩了），相应的 1 经度间的横向距离为 L*cosA/360。

⾚道的实际周约长为40000km，代⼊上⾯的公式就可以⼤致估算出 1 纬度间的纵向距离为 111km，纬度为A的地区的 1 经度间的横向距离为 cosA*111km。

北半球纬度、经度的1度1分1秒对应的⽅向、距离各是多少？⼀、不同纬度的间距差是相同的，纬度（⾚道）⼀度合110.94公⾥，⼀分合1.849公⾥，⼀秒合30.8⽶。

纬度数值加⼤时，位置北移，减⼩时则位置南移。

⼆、经度差对应的东西⽅向距离因其所处的纬度不同⽽不同，在北半球的东经差数见下表：纬度东半球经度差对应的东西⽅向距离1°1′1″北纬51°70公⾥ 1.17公⾥19.50⽶北纬44°80公⾥ 1.33公⾥22.21⽶北纬40°85.3公⾥ 1.42公⾥23.69⽶北纬36°90公⾥ 1.50公⾥25.00⽶北纬30°96公⾥ 1.60公⾥26.67⽶北纬26°100公⾥ 1.67公⾥27.78⽶北纬20°104公⾥ 1.73公⾥28.89⽶由表中可知：北纬36°时，经度1度合 90公⾥，⼀分合1500⽶，⼀秒合25⽶。

经度数值加⼤时，位置东移，减⼩时则位置西移。

地球上两点的经纬度计算他们距离的公式一、球面余弦定理球面余弦定理是一种常用的计算地球上两点距离的公式。

它基于球面三角形的余弦定理，公式如下：d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))其中，d表示两点之间的距离，R表示地球的半径，而lat1、lat2、lon1和lon2分别表示两点的纬度和经度。

在计算中，经纬度应以弧度为单位。

如果给定的经纬度是度数，可以先将其转化为弧度再代入公式中计算。

二、哈弗斯因子公式哈弗斯因子公式也是一种常用的计算地球上两点距离的公式。

它基于海伦公式，公式如下：d = 2 * R * arcsin(√(sin((lat2 - lat1) / 2)² + cos(lat1) * cos(lat2) * sin((lon2 - lon1) / 2)²))其中，d表示两点之间的距离，R表示地球的半径，而lat1、lat2、lon1和lon2分别表示两点的纬度和经度。

在计算中，经纬度应以弧度为单位。

如果给定的经纬度是度数，可以先将其转化为弧度再代入公式中计算。

可以看到，球面余弦公式和哈弗斯因子公式在计算方式上有一些差异。

球面余弦公式更容易计算，因为它不需要计算所有角度的正弦函数值，只需要计算两个角度的正弦函数值并进行一些乘法和加法运算。

相比之下，哈弗斯因子公式需要计算所有角度的正弦函数值，计算量稍大一些。

无论是使用球面余弦公式还是哈弗斯因子公式，都需要注意地球的半径值。

地球的半径并不是一个精确的常数，因为地球的形状是复杂的。

在实际计算中，可以根据所需要的精度选择合适的地球半径值，一般情况下选择平均半径值进行计算即可。

除了上述公式之外，还可以使用其他更复杂的公式来计算地球上两点的距离。

例如，Vincenty公式和Haversine公式等都是比较常用的计算地球上两点距离的公式。

坐标点的距离如何计算在地图定位、导航、地理信息系统等领域中，计算两个坐标点之间的距离是一项基本的任务。

无论是计算两个地理位置之间的直线距离，还是计算驾车路径上的实际距离，都离不开坐标点距离的计算。

本文将介绍几种常用的计算坐标点距离的方法。

1. 平面坐标系在平面坐标系中，我们可以使用两点之间的欧几里得距离来计算点的距离。

欧几里得距离是两点间的直线距离，用勾股定理来计算。

设两点的坐标分别为(x1, y1)和(x2, y2)，则它们之间的距离d可以通过以下公式计算：d = \\sqrt{(x2 - x1)^2 + (y2 - y1)^2}这个公式是通过计算两点在x轴和y轴上的距离差的平方和，再开平方根得到的。

这种方式适用于平面上的二维点的距离计算。

2. 球面坐标系在地理信息系统中，常常需要计算两个地理位置之间的距离。

由于地球是一个近似于椭球的三维物体，所以球面距离计算需要考虑地球的曲率。

常用的球面距离计算方法有以下两种：2.1 大圆距离大圆距离是计算地球上两个点之间最短路径的方法。

这种距离计算方式需要使用经纬度坐标。

设两点的经纬度分别为(lat1, lon1)和(lat2, lon2)，则它们之间的大圆距离d可以通过以下公式计算：d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(l on2 - lon1))这里R是地球的半径，取平均半径约为6371公里。

这种方法使用了球面三角关系，通过计算两点的纬度和经度之差的余弦值，再使用反余弦函数计算出最终的距离。

2.2 Haversine公式Haversine公式是大圆距离的一种近似计算方法，用于计算球面上两点之间的距离。

设两点的经纬度分别为(lat1, lon1)和(lat2, lon2)，则它们之间的Haversine距离d可以通过以下公式计算：a = sin^2((lat2 - lat1) / 2) + cos(lat1) * cos(lat2) * sin^2((lon2 - lon1) / 2)c = 2 * atan2(sqrt(a), sqrt(1 - a))d = R * c其中，a是一个中间变量，c是两点之间的角距离，d是最终的距离。

excel经纬度距离计算公式经纬度距离计算公式是一种用于计算地球上两点之间距离的公式。

在Excel中，我们可以使用该公式来计算两个经纬度坐标之间的距离，这对于地理信息系统(GIS) 和其他需要计算地理距离的应用程序非常有用。

该公式基于海卫一号卫星计算公式，其核心思想是根据两个经纬度坐标之间的球面距离来计算两点之间的距离。

由于地球是一个略微扁平的球体，球面距离比直线距离更准确。

该公式的基本形式如下：距离= 6371.01 * ACOS(COS(RADIANS(90 - 纬度1)) * COS(RADIANS(90 - 纬度2)) + SIN(RADIANS(90 - 纬度1)) * SIN(RADIANS(90 - 纬度2)) * COS(RADIANS(经度1 - 经度2)))其中，6371.01是地球半径（单位是千米），纬度和经度是以度为单位的坐标值，RADIANS是将角度转换为弧度的函数，ACOS是反余弦函数，COS和SIN是余弦和正弦函数。

在Excel中，我们可以使用以下公式来计算两点之间的距离：= 6371.01 * ACOS(COS(RADIANS(90 - 纬度1)) * COS(RADIANS(90 - 纬度2)) + SIN(RADIANS(90 - 纬度1)) * SIN(RADIANS(90 - 纬度2)) * COS(RADIANS(经度1 - 经度2)))其中，纬度1和经度1是第一个点的坐标，纬度2和经度2是第二个点的坐标。

当我们输入这个公式后，Excel会自动计算出两个经纬度坐标之间的距离，并将结果显示在单元格中。

该公式可以用于计算任意两个地点之间的距离，无论它们位于世界的哪个角落。

需要注意的是，该公式仅适用于计算球面距离，而不考虑地球表面的复杂形状和地形。

在实际应用中，我们可能需要考虑其他因素，例如海拔高度、地形等，以更准确地计算地球上两点之间的实际距离。

经纬度距离计算公式是一种非常有用的工具，它可以帮助我们快速、准确地计算地球上任意两点之间的距离。

经纬度计算距离计算公式经纬度计算距离计算公式1. Haversine公式Haversine公式是一种常用的计算地球上两点间距离的公式。

它基于球面三角学原理，通过经纬度计算出两点间的弧长，然后转换为实际距离。

公式：d=2rarcsin(√sin2((θ2−θ1)/2)+cos(θ1)⋅cos(θ2)⋅sin2((λ2−λ1)/2))其中，d为两点间距离，r为地球半径，θ1和λ1为第一个点的纬度和经度，θ2和λ2为第二个点的纬度和经度。

示例：假设第一个点的坐标为(, -)，第二个点的坐标为(, -)。

采用地球半径r=6371千米（常用值），代入Haversine公式进行计算，可以得到两点之间的距离为约千米。

2. Vincenty公式Vincenty公式是一种更为精确的计算地球上两点间距离的公式。

它考虑了地球的椭球形状，通过迭代计算，可以得到更准确的结果。

公式：a=r1⋅r2⋅sin(θ2−θ1)2+r2⋅r3⋅sin(θ3−θ2)2b=r1⋅r2⋅cos(θ2−θ1)−r2⋅r3cos(θ3−θ2)c=r1⋅r3⋅cos(θ3−θ1)−r2⋅r3⋅cos(θ3−θ2) d=arctan(r2⋅r3sin(θ3−θ2)⋅cos(θ3−θ1)r1⋅r2⋅sin(θ2−θ1)⋅cos(θ3−θ2)+r1⋅r3⋅sin(θ3−θ1)⋅cos(θ2−θ1))latitude=θ1+c⋅cos(A)−b⋅sin(A)r2λ2=λ1+d r2d=r1⋅arcsin(sin(θ2−θ1)⋅cos(θ3)⋅sin(θ2−θ1)+cos(θ1)⋅cos(θ2)⋅sin2(λ3−λ2))其中，d为两点间距离，r1、r2、r3分别为两个点的纬度、经度对应的椭球半径，θ1和λ1为第一个点的纬度和经度，θ2和λ2为第二个点的纬度和经度，θ3和λ3为两点连线在球面上的方位角，A为初始猜测的方位角。

示例：以第一个点的坐标为(, -)，第二个点的坐标为(, -)，根据Vincenty公式进行计算，可以得到两点之间的距离为约千米。

多个地点间的距离计算公式在现代社会，人们经常需要计算不同地点之间的距离，比如出行规划、物流配送等。

而地点之间的距离计算公式就成为了一个重要的工具。

本文将介绍一些常用的地点间距离计算公式，并对它们进行简要的分析和比较。

1. 直线距离计算公式。

直线距离是最简单的距离计算方式，它是通过两个地点的经纬度坐标来计算的。

假设地点A的经纬度坐标为（A1, A2），地点B的经纬度坐标为（B1, B2），则地点A和地点B之间的直线距离可以通过以下公式计算：d = R arccos(sin(A1)sin(B1) + cos(A1)cos(B1)cos(A2-B2))。

其中，R为地球半径，一般取平均值6371km。

这个公式的优点是简单易用，缺点是没有考虑地球表面的曲率和地形的影响，只适用于较短距离的计算。

2. 大圆航线距离计算公式。

大圆航线距离是指两地之间在地球表面上的最短距离，也是飞行航线的最佳路径。

它的计算公式如下：d = R arccos(sin(A1)sin(B1) + cos(A1)cos(B1)cos(A2-B2))。

这个公式与直线距离的公式是相同的，但它更适用于长距离的计算，因为它考虑了地球表面的曲率。

在航空航线规划和航海导航中广泛使用。

3. 曼哈顿距离计算公式。

曼哈顿距离是指两点在标准坐标系上的距离，即沿着坐标轴的距离之和。

对于二维坐标系来说，两点（x1, y1）和（x2, y2）之间的曼哈顿距离可以通过以下公式计算：d = |x1 x2| + |y1 y2|。

这个公式的优点是简单直观，适用于城市道路网格等直线交错的环境，缺点是没有考虑地球曲面的影响。

4. Haversine距离计算公式。

Haversine距离是一种用于计算两点间球面距离的方法，它考虑了地球的曲率和地球半径的变化。

对于地球上两点之间的距离，Haversine距离的计算公式如下：a = sin²((Δφ)/2) + cos(φ1) cos(φ2) sin²((Δλ)/2)。

地球两点间距离计算公式地球是人类生活的家园，了解地球上两点之间的距离对于我们的生活和探索更大世界都具有重要意义。

在这篇文章中，我们将介绍一种用于计算地球两点间距离的公式——球面距离公式，并解释如何使用这个公式来计算距离。

球面距离公式是基于地球的球形结构和球面几何原理推导出来的。

在地球上，我们通常使用经度和纬度来表示一个地点的位置。

经度表示一个地点在东西方向上的位置，而纬度表示一个地点在南北方向上的位置。

使用经纬度来计算两个地点之间的距离涉及到计算两者之间的角度差。

首先，我们需要将经纬度转换成弧度单位，因为角度单位在三角函数中使用。

经度的范围是从0°到360°，纬度的范围是从-90°到90°。

而弧度的范围是从0到2π。

我们可以使用以下公式将经纬度转换为弧度：角度（弧度）= 角度（度数）× π / 180转换完成后，我们可以使用以下公式来计算两个点之间的球面距离：距离 = 地球半径× arccos（sin(纬度1) × sin(纬度2) +cos(纬度1) × cos(纬度2) × cos(经度1 - 经度2)）在这个公式中，地球半径是一个常数，通常取平均值约为6371千米，但可以根据需要进行调整。

现在让我们通过一个实际的例子来应用这个公式。

假设我们想计算位于巴黎（经度：2.3522°E，纬度：48.8566°N）和纽约（经度：74.0060°W，纬度：40.7128°N）之间的球面距离。

首先，将经纬度转换成弧度：巴黎的经度（弧度）= 2.3522 × π / 180 ≈ 0.041巴黎的纬度（弧度）= 48.8566 × π / 180 ≈ 0.853纽约的经度（弧度）= 74.0060 × π / 180 ≈ 1.291纽约的纬度（弧度）= 40.7128 × π / 180 ≈ 0.711将这些值代入球面距离公式，我们可以计算出两个城市之间的距离：距离= 6371 × arccos（sin(0.853) × sin(0.711) +cos(0.853) × cos(0.711) × cos(1.291 - 0.041)）通过计算，我们得到的结果约为5,977.59千米。

地球上两点距离公式
嘿，朋友们！今天咱就来聊聊地球上两点距离公式。

这公式啊，就像是一把神奇的钥匙，能帮我们解开地球这个大球体上两点之间距离的秘密呢！
常见的公式就是根据经纬度来计算的呀。

比如说，有两个地方，一个在北京，经纬度是（东经 116 度，北纬 40 度），另一个在上海，经纬度是（东经 121 度，北纬 31 度）。

通过这个公式，我们就能算出它们之间大概有多远啦。

这多有意思啊，就好像我们有了一双能穿透地球的眼睛，可以看到两点之间的“距离之路”呢！难道这还不够神奇吗？就好比你想知道从你家到好朋友家在地球上“画”出的这条线有多长，这个公式就能告诉你答案哟！哈哈，明白了吧！
所以啊，大家可别小看这个小小的公式，它用处可大着呢！就像是一把开启地球奥秘之门的钥匙，让我们能更深入地了解我们生活的这个星球呀！。

根据两点经纬坐标计算两点间的距离[JAVA]解决此问题的关键是要理解空间⼏何模型，在理解空间⼏何模型的基础上再利⽤数学公式求取两点之间的值。

其解决步骤如下：1、设两点分别为P1、P2，如果其值是⽤度分秒形式表⽰，则需将其转换成⼗进制度的形式，如P1点纬度为23度30分，则其纬度值转换成⼗进制度的形式为23.5度。

如果值为⼗进制度的形式，则直接进⼊第⼆步。

2、分别将两点的经度、纬度值转换成弧度制形式，如P1纬度为23.5度，转换成弧度制则为：23.5*PI / 180。

分别⽤ P1latInRad、P1LongInRad、P2latInRad、P2LongInRad表⽰。

3、分别求取两点间的纬度差（dlat）与经度差（dlon）；4、求取两点间的正弦与余弦值，公式如下：A=sin2(dlat/2) + cos(P1LatInRad)*cos(P2LatInRad)*Sin2(dlon/2) (1)5、求取两点的正切值，公式如下：C=2*Math.Atan2(Math.Sqrt(A), Math.Sqrt(1-A)) (2)6、返回两点间的距离：公式如下：D=EarthRadiusKm * C (3)public class distCnvter {private final static double PI = 3.14159265358979323; // 圆周率private final static double R = 6371229; // 地球的半径public static double getDistance(double longt1, double lat1, double longt2,double lat2) {double x, y, distance;x = (longt2 - longt1) * PI * R* Math.cos(((lat1 + lat2) / 2) * PI / 180) / 180;y = (lat2 - lat1) * PI * R / 180;distance = Math.hypot(x, y);return distance;}}。

根据经纬度计算地⾯两点间的距离-数学公式及推导1.假设：地球是正球体。

地⾯两点A和B的经纬度坐标分别为(Aj,Aw)和(Bj,Bw),地球半径R取平均值6371km。

2.建⽴三维直⾓坐标系：地球球⼼为原点O，地轴为Z轴，北极⽅向为Z轴正⽅向，⾚道平⾯为X轴和Y轴所在平⾯，在该平⾯上地⼼到零度经线的⽅向为X轴正⽅向，根据右⼿定则确定Y轴正⽅向。

设点A的三维坐标为(Ax,Ay,Az)，点B的三维坐标为(Bx,By,Bz)3.思路：A、B、O三点所在平⾯与地球相交形成⼀个半径为R的圆，求AB间的地⾯距离就是求该圆上圆弧AB的长度。

可由弧长等于半径乘以圆⼼⾓公式求得。

由于R是确定的，只要获得OA与OB的夹⾓θ就可以获得弧AB的长度。

弧AB=R*θ。

⾓θ可通过向量公式求得：向量OA*向量OB=|OA||OB|cosθ。

则cosθ=向量OA*向量OB/|OA||OB|=(Ax*Bx+Ay*By+Az*Bz)/R*R4.⽤经纬度坐标表⽰三维直⾓坐标：Ax=R*cosAw*cosAjAy=R*cosAw*sinAjAz=R*sinAwBx=R*cosBw*cosBjBy=R*cosBw*sinBjBz=R*sinBw代⼊可得cosθ=cosAw*cosAj*cosBw*cosBj+cosAw*sinAj*cosBw*sinBj+sinAw*sinBw=cosAw*cosBw(cosAj*cosBj+sinAj*sinBj)+sinAw*sinBw=cosAw*cosBw*cos(Aj-Bj)+sinAw*sinBwθ=arccos[cosAw*cosBw*cos(Aj-Bj)+sinAw*sinBw]5.综上可得根据经纬度计算地⾯两点间距离的公式：弧AB=R*arccos[cosAw*cosBw*cos(Aj-Bj)+sinAw*sinBw]说明：类似的公式推导⼤家以前都做过，时间久了可能会忘记⼀些东西，于是我把它记了下来，以备查阅。

经纬度互换、换算成⽶、两点的经纬度计算两点间的距离GPS坐标系我本⾝不太了解它跟⾕歌地图经纬度有多⼤区别，于是搜了⼀下，看看他们的区别：地形图坐标系：我国的地形图采⽤⾼斯－克吕格平⾯直⾓坐标系。

在该坐标系中，横轴：⾚道，⽤Ｙ表⽰；纵轴：中央经线，⽤Ｘ表⽰；坐标原点：中央经线与⾚道的交点，⽤0表⽰。

⾚道以南为负，以北为正；中央经线以东为正，以西为负。

我国位于北半球，故纵坐标均为正值，但为避免中央经度线以西为负值的情况，将坐标纵轴西移500公⾥。

北京54坐标系：1954年我国在北京设⽴了⼤地坐标原点，采⽤克拉索夫斯基椭球体，依此计算出来的各⼤地控制点的坐标，称为北京54坐标系。

GS84坐标系：即世界通⽤的经纬度坐标系。

经纬度表⽰：1884年国际经度会议规定，以通过英国伦敦格林威治天⽂台⼦午仪中⼼的经线为0°经线。

从0°经线往东叫东经，往西叫西经，东、西各分180°。

习惯上以西经20°和东经160°为分界把地球分为东西两个半球。

假如从地轴的正中间将地球切成南北两半，上边的⼀半叫北半球，下边的⼀半叫南半球。

被切的这个平⾯，叫⾚道⾯。

⾚道⾯与地球表⾯相交的线叫⾚道。

纬线从⾚道往两极越来越短，到了两极就缩⼩成⼀个点了。

科学家们把⾚道定为0°纬线，从⾚道向两极各分为90°，⾚道以南叫南纬，⾚道以北叫北纬。

在计算机或GPS上经纬度经常⽤度、分、秒和度.度、分.分、秒.秒的混合⽅式进⾏表⽰，度、分、秒间的进制是60进制，度.度、分.分、秒.秒的进制是100进制，换算时⼀定要注意。

可以近似地认为每个纬度之间的距离是不变的111KM,每分间 1.85KM，每秒间31.8M。

经度间的距离随纬度增⾼逐渐减⼩，可按以下公式计算：经度1°长度=111.413cosφ⼀0.094cos3φ公⾥(纬度φ处)。

⼀般从GPS得到的数据是经纬度。

经纬度有多种表⽰⽅法。

两点坐标计算距离方位角计算两点之间的距离和方位角是在几何学和地理学中常见的问题。

这个问题可以在平面参数坐标系和球面坐标系下进行计算。

1.平面参数坐标系下的计算：在平面参数坐标系下，我们可以使用勾股定理计算两点之间的距离。

设两点的坐标分别为(x1,y1)和(x2,y2)，则两点之间的距离d可以通过以下公式计算：d=√((x2-x1)²+(y2-y1)²)此公式可以直接计算出两点之间的直线距离。

如果我们想要计算方位角，我们可以使用反三角函数来计算。

设两点之间的水平距离为dx，垂直距离为dy，则角度θ可以通过以下公式计算：θ = atan2(dy, dx)这里的atan2函数是一个广义反正切函数，它可以处理各种情况下的角度计算。

2.球面坐标系下的计算：在球面坐标系下，我们可以利用经纬度来计算两点之间的距离和方位角。

设两点的经纬度分别为(λ1,φ1)和(λ2,φ2)，则两点之间的距离D可以通过以下公式计算：D = R * arcos(sin(φ1) * sin(φ2) + cos(φ1) *cos(φ2) *cos(λ1 - λ2))其中，R是地球的半径。

方位角的计算需要一些额外的步骤。

首先，我们需要计算两点之间的经度差Δλ。

然后，我们可以使用以下公式计算方位角α：α = atan2(sin(Δλ) * cos(φ2), cos(φ1) * sin(φ2) -sin(φ1) * cos(φ2) * cos(Δλ))与之前的计算方式类似，这里也使用了广义反正切函数来处理角度计算。

需要注意的是，以上计算公式都是基于理想情况下的计算，并不考虑地球的真实形状和非均匀性。

如果需要更精确的计算结果，可以使用更复杂的模型和算法来进行计算。

总结起来，计算两点之间的距离方位角可以根据使用的坐标系不同而变化。

在平面参数坐标系下，可以使用勾股定理和反三角函数进行计算；在球面坐标系下，可以使用经纬度和球面三角函数进行计算。

地球是一个近乎标准的椭球体，它的赤道半径为6378.140千米，极半径为6356.755千米，平均半径6371.004千米。

如果我们假设地球是一个完美的球体，那么它的半径就是地球的平均半径，记为R。

如果以0度经线为基准，那么根据地球表面任意两点的经纬度就可以计算出这两点间的地表距离（这里忽略地球表面地形对计算带来的误差，仅仅是理论上的估算值）。

设第一点A的经纬度为(LonA, LatA)，第二点B的经纬度为(LonB, LatB)，按照0度经线的基准，东经取经度的正值(Longitude)，西经取经度负值(-Longitude)，北纬取90-纬度值(90- Latitude)，南纬取90+纬度值(90+Latitude)，则经过上述处理过后的两点被计为(MLonA, MLatA)和(MLonB, MLatB)。

那么根据三角推导，可以得到计算两点距离的如下公式：C = sin(MLatA)*sin(MLatB)*cos(MLonA-MLonB) +cos(MLatA)*cos(MLatB)Distance = R*Arccos(C)*Pi/180这里，R和Distance单位是相同，如果是采用6371.004千米作为半径，那么Distance就是千米为单位，如果要使用其他单位，比如mile，还需要做单位换算，1千米=0.621371192mile如果仅对经度作正负的处理，而不对纬度作90-Latitude(假设都是北半球，南半球只有澳洲具有应用意义)的处理，那么公式将是：C = sin(LatA)*sin(LatB) +cos(LatA)*cos(LatB)*cos(MLonA-MLonB)Distance = R*Arccos(C)*Pi/180以上通过简单的三角变换就可以推出。

如果三角函数的输入和输出都采用弧度值，那么公式还可以写作：C = sin(LatA*Pi/180)*sin(LatB*Pi/180) +cos(LatA*Pi/180)*cos(LatB*Pi/180)*cos((MLonA-MLonB)*Pi/180) Distance = R*Arccos(C)*Pi/180也就是：C = sin(LatA/57.2958)*sin(LatB/57.2958) +cos(LatA/57.2958)*cos(LatB/57.2958)*cos((MLonA-MLonB)/57.295 8)Distance = R*Arccos(C) = 6371.004*Arccos(C) kilometer =0.621371192*6371.004*Arccos(C) mile =3958.758349716768*Arccos(C) mile。

经纬度与距离换算公式
同一纬线上,经度相差一度,距离相差111KM乘以cos该纬度数.赤道上,经度相差一度,距离相差111KM；cos纬度数×经度差×111km 同一经度：纬度差×111km
不在同一纬线或同一经线上的就另当别论,
具体分析.a）在纬度相等的情况下：
经度每隔0.00001度，距离相差约1米；
每隔0.0001度，距离相差约10米；
每隔0.001度，距离相差约100米；
每隔0.01度，距离相差约1000米；
每隔0.1度，距离相差约10000米。

b）在经度相等的情况下：
纬度每隔0.00001度，距离相差约1.1米；
每隔0.0001度，距离相差约11米；
每隔0.001度，距离相差约111米；
每隔0.01度，距离相差约1113米；
每隔0.1度，距离相差约11132米。

根据两点经纬度计算距离这些经纬线是怎样定出来的呢？地球是在不停地绕地轴旋转（地轴是一根通过地球南北两极和地球中心的假想线），在地球中腰画一个与地轴垂直的大圆圈，使圈上的每一点都和南北两极的距离相等，这个圆圈就叫作“赤道”。

在赤道的南北两边，画出许多和赤道平行的圆圈，就是“纬圈”；构成这些圆圈的线段，叫做纬线。

我们把赤道定为纬度零度，向南向北各为90度，在赤道以南的叫南纬，在赤道以北的叫北纬。

北极就是北纬90度，南极就是南纬90度。

纬度的高低也标志着气候的冷热，如赤道和低纬度地地区无冬，两极和高纬度地区无夏，中纬度地区四季分明。

其次，从北极点到南极点，可以画出许多南北方向的与地球赤道垂直的大圆圈，这叫作“经圈”；构成这些圆圈的线段，就叫经线。

公元1884平面坐标图年，国际上规定以通过英国伦敦近郊的格林尼治天文台的经线作为计算经度的起点，即经度零度零分零秒，也称“本初子午线”。

在它东面的为东经，共180度；在它西面的为西经，共180度。

因为地球是圆的，所以东经180度和西经180度的经线是同一条经线。

各国公定180度经线为“国际日期变更线”。

为了避免同一地区使用两个不同的日期，国际日期变线在遇陆地时略有偏离。

每一经度和纬度还可以再细分为60分，每一分再分为60秒以及秒的小数。

利用经纬线，我们就可以确定地球上每一个地方的具体位置，并且把它在地图或地球仪上表示出来。

例如问北京的经纬度是多少？我们很容易从地图上查出来是东经116度24分，北纬39度54分。

在大海中航行的船只，只要把所在地的经度测出来，就可以确定船在海洋中的位置和前进方向。

纬度共有90度。

赤道为0度，向两极排列，圈子越小，度数越大。

横线是纬度，竖线是经度。

当然可以计算，四元二次方程。

经度和纬度都是一种角度。

经度是个两面角，是两个经线平面的夹角。

因所有经线都是一样长，为了度量经度选取一个起点面，经1884年国际会议协商，决定以通过英国伦敦近郊、泰晤士河南岸的格林尼治皇家天文台（旧址）的一台主要子午仪十字丝的那条经线为起始经线，称为本初子午线。

知经纬度计算两点精确距离
知经纬度计算两点精确距离
摘要本文阐述了用程序计算在已知两点经纬度情况下，精确计算两点之间距离的方法，达到日常地震资料分析中准确定位、减少工作量的目的。

关键词经度；纬度；地震资料
0 引言
地震分析中很多时候需要计算地球上两点之间的精确距离，而这两点之间距离计算公式比较复杂，而且容易出错。

根据这些问题，用《Visual Basic》编写了《知经纬度计算两点精确距离》程序，使两点之间距离计算变得简单，为地震分析提供了方便而快捷的计算工具。

1 计算公式
国家地震局地球物理所编制的《近震分析》中可以知道，在地面上计算两点距离的一般方法有：
1）在大比例地图上直接测量
在地图上根据比例直接换算距离，方法比较简单。

2）已知两点的大地坐标计算距离
设两点大地坐标值为（x1,y1），（x2,y2）则：
Δ=
式中Δ是两点之间距离，单位是公里。

用此公式计算时，要注意两点是否在同一个坐标系内。

如果两点不在同一个坐标系内，就须将其中的一点经坐标平移变换到另一点所在的坐标系内。

平移公式为：、式中a，b 是原坐标的原点在新坐标系中的坐标值。

3）知两点的经纬度计算两点距离的近似公式
设定A点（纬度, 经度）和B点（纬度，经度）则
这4种方法互相比较有如下特点：
第1种方法，直观易行，也是常用方法。

即使要采用其他方法计算，也常常。