下载文档原格式
课题：约分与通分1．经历探索分式约分和通分的过程，理解约分、通分的意义、依据和方法．2．能正确、熟练地运用分式的基本性质进行约分和通分．3．掌握最简分式、最简公分母的概念．重点：利用分式的基本性质进行约分、通分．难点：分子、分母是多项式的分式的约分和通分．一、情景导入，感受新知1．请同学们考虑：34与1520相等吗？924与38相等吗？为什么？ 2．说出34与1520之间变形的过程，924与38之间变形的过程，并说出变形依据． 二、自学互研，生成新知【自主探究】(一)阅读教材P 130思考～P 131例3，完成下面的内容：约分：1824＝18÷624÷6＝34，根据是分数的基本性质． 类比分数的约分，我们可以完成以下填空：(1)6a 2b 38a 3b 2＝3b 4a ；(2)x 2＋xy x 2＝x ＋y x． 上述过程的根据是分式的基本性质．【合作探究】1．利用分式的基本性质化简． (1)36ab 3c 6abc 2； 解：原式＝6abc ·6b 26abc ·c＝6b 2c ； (2)－8a 2bc 2－12a 2b 2c； 解：原式＝4a 2bc ·2c 4a 2bc ·3b ＝2c 3b；(3)x 2－2x 4－x 2； 解：原式＝x （x －2）－（x ＋2）（x －2）＝－x x ＋2； (4)a 2－16a 2＋8a ＋16. 解：原式＝（a －4）（a ＋4）（a ＋4）2＝a －4a ＋4. 2．观察化简后的分式有什么发现？归纳：根据分式的基本性质把一个分式的分子与分母的公因式约去，叫做分式的约分；分子与分母没有公因式的分式，叫做最简分式．(二)阅读教材P 131思考～P 132例4，完成下面的内容：通分：12＝1×62×6＝612；34＝3×34×3＝912；56＝5×26×2＝1012． 上述通分的依据是分数的基本性质． 归纳：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式的过程，叫做分式的通分．分式通分的关键是确定最简公分母．确定最简公分母的方法：(1)系数：取各分母中系数的最小公倍数．(2)字母：取各分母中所有出现的字母或因式．(3)指数：相同字母或因式取最高次幂．师生活动①明了学情：学生自主学习，教师巡视全班．②差异指导：对于自学中遇到的问题适时点拨．③生生互助：先自学，对于困惑，同桌、小组交流．三、典例剖析，运用新知【合作探究】例1：将下列分式通分：(1)12与1x ； (2)32a 与43a 2b. 【分析】(1)把分式化成分母相同的分式的过程叫做分式的通分；(2)通分的关键是确定几个分式的最简公分母，而确定最简公公母通常按以下三个步骤进行：①取各分母系数的最小公倍数作为公分母系数；②各个分母中所有不同的因式均作为公分母中的一个因式；③所有因式的指数以它的最高次幂作为公因式中该因式的指数．解：(1)最简公分母是：2x ，∴12＝1·x 2x ＝x 2x ，1x ＝1×2x ·2＝22x； (2)最简公分母是6a 2b ，∴32a ＝3·3ab 2a ·3ab ＝9ab 6a 2b ，43a 2b ＝4×23a 2b ·2＝86a 2b. 例2：填空：(1)b ＋1a ＋c ＝（ ）an ＋cn； (2)x 2－y 2（x ＋y ）2＝x －y （ ）. 【分析】对等式两边的分子、分母因式分解，比较后分别对分子、分母同乘以一个不为0的数．解：(1)bn ＋n ；(2)x ＋y.例3：约分：(1)－4x 2yz 315xyz 5； (2)2（x －y ）3y －x. 【分析】约分就是分式的分子、分母同除以一个不为0的数．解：(1)－4x 15z 2；(2)－2(x －y)2. 师生活动①明了学情：学生自主学习，教师巡视全班．②差异指导：对于自学中遇到的问题适时点拨．③生生互助：先自学，对于困惑，同桌、小组交流．四、课堂小结，回顾新知1．通过本节课的学习，你有哪些收获？2．通过这节课的学习，你觉得有哪些知识是难以把握的？你有何想法？五、检测反馈、落实新知1．下列分式是最简分式的是( B )A .2a 3a 2bB .a ＋b a 2＋b 2C .a a 2－3aD .a 2－ab a 2－b 22．分式23a ，a ＋1－2a ，2a －14a 2的最简公分母是( C )A ．24a 6B ．24a 3C ．12a 2D ．6a 33．下列约分正确的是( A )A .x ＋y x 2＋xy ＝1xB .x ＋y x ＋y＝0 C .x 6x 2＝x 3 D .2xy 24x 2y ＝124．将|a －b|a －b约分，正确的结果是( C ) A ．1 B ．2C ．±1D ．无法确定5．已知x 2＋3x ＋1＝0，求x 2＋1x 2的值． 解：由题意知：x ≠0，等式x 2＋3x ＋1＝0两边同除以x 得：x ＋3＋1x ＝0，∴x ＋1x＝－3. ∴x 2＋1x 2＝⎝⎛⎭⎫x ＋1x 2－2x·1x＝(－3)2－2＝7. 六、课后作业：巩固新知(见学生用书)。
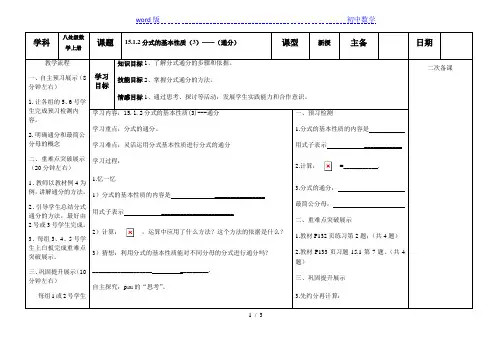
学科八处级数学上册课题15.1.2分式的基本性质（3）——（通分）课型新授主备日期教学流程一、自主预习展示（8分钟左右）1.让各组的5、6号学生完成预习检测内容。
2.明确通分和最简公分母的概念二、重难点突破展示（20分钟左右）1、教师以教材例4为例，讲解通分的方法。
2、引导学生总结分式通分的方法，最好由2号或3号学生完成。
3、每组3、4、5号学生上白板完成重难点突破展示。
三、巩固提升展示（10分钟左右）每组1或2号学生学习目标知识目标1、了解分式通分的步骤和依据。
技能目标2、掌握分式通分的方法。
情感目标1、通过思考、探讨等活动，发展学生实践能力和合作意识。
二次备课学习内容：15.1.2分式的基本性质(3)---通分学习重点：分式的通分。
学习难点：灵活运用分式基本性质进行分式的通分学习过程：1.忆一忆1）分式的基本性质的内容是________________用式子表示_______________________2）计算：，运算中应用了什么方法？这个方法的依据是什么？3）猜想：利用分式的基本性质能对不同分母的分式进行通分吗？___________________ _________.自主探究：p131的“思考”。
一、预习检测1.分式的基本性质的内容是用式子表示____________2.计算：=___________.3.分式的通分：最简公分母：二、重难点突破展示1.教材P132页练习第2题；（共4题）2.教材P133页习题15.1第7题。
（共4题）三、巩固提升展示3.先约分再计算：1 / 3分析巩固提升展示中的习题，让其它学生抢答上白板展示或自己上白板展示。
四、小结（2分钟左右）留1-2分钟时间让学生自己小结一下本节课的学习收获。
归纳：分式的通分：2.看一看教师出示例题，P132页例4。
通过例题使学生明白通分的关键是准确找出各分式的最简公分母：3.练一练1）完成教材P132页练习2通分2）完成教材P133页习题15.1第7题通分4.小结（1）（2）课后反思教研组查阅包组领导查阅2 / 33 / 3。
