简谐振动的运动方程

一维简谐振动方程简谐振动是指物体在沿着直线方向上进行往复运动的一种振动形式。

简谐振动方程是描述简谐振动过程中物体位移与时间的关系的方程。

它可以用数学方式表示为：x(t) = A * cos(ωt + φ)其中，x(t)表示振动物体在时间t时刻的位移；A表示振幅，即位移的最大值；ω表示角频率，它与周期T的关系是ω=2π/T；φ表示初相位，它决定了位移曲线的起始位置。

简谐振动的特点是周期性和对称性。

周期性是指振动物体以一定的时间间隔重复相同的位移值。

对称性是指振动物体出现正向位移和反向位移的时间是对称的。

根据简谐振动方程，我们可以推导出一些重要的物理量和特性。

首先是振动周期T，它表示振动物体完成一个完整振动往复运动所需要的时间。

根据角频率与周期的关系，可以得到T=2π/ω。

其次是振动频率f，它表示振动物体每秒钟振动的次数。

振动频率与角频率的关系是f=ω/2π。

再次是振动速度v和加速度a，它们分别表示振动物体在给定时刻的速度和加速度。

根据位移x关于时间的一阶和二阶导数，可以得到振动速度和加速度的表达式：v(t) = dx(t)/dt = -Aωsin(ωt + φ)a(t) = dv(t)/dt = -Aω²cos(ωt + φ)振动速度和加速度的正负号与振动物体的位置有关。

当x(t)为正时，振动速度为负，即物体向负方向运动；当x(t)为负时，振动速度为正，即物体向正方向运动。

同样地，当x(t)为正时，振动加速度为正；当x(t)为负时，振动加速度为负。

简谐振动还有一个重要的特性是能量守恒。

振动物体由于受到弹力恢复力的作用而具有动能和势能。

动能由振动物体的速度决定，势能由振动物体的位移决定。

在一个振动周期内，动能和势能之间不断转化，但总能量保持不变。

具体地说，简谐振动的总能量等于振动物体的最大势能或动能，可以表示为：E=1/2kA²其中，k表示振动系统的弹性系数，它与物体的质量m和振动频率f之间的关系是k = 4π²mf²。

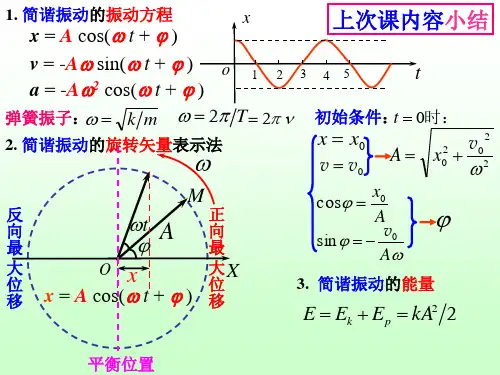
简谐振动运动方程简谐振动是物理学中一种重要的振动形式，它在自然界和工程领域中都有广泛应用。

简谐振动的运动方程描述了振动物体在平衡位置附近的周期性运动规律，可以用于解释弹簧振子、摆钟、电路中的振荡电流等现象。

简谐振动的运动方程可以表示为x = A*cos(ωt+φ)，其中x表示振动物体距离平衡位置的位移，A表示振幅，ω表示角频率，t表示时间，φ表示初相位差。

这个方程描述了振动物体随时间变化的位置情况。

简谐振动的周期是指振动物体完成一次完整振动所需要的时间。

周期T与角频率ω之间有关系T = 2π/ω。

振动的频率则是指单位时间内完成的振动次数，可以表示为 f = 1/T = ω/2π。

振动的频率与角频率是相互关联的，它们描述了振动物体的快慢程度。

简谐振动的振幅是指振动物体离开平衡位置的最大位移量。

振幅越大，振动物体的运动范围就越大。

振动物体的能量也与振幅有关，振幅越大，能量越高。

振幅与振动物体的势能和动能之间也存在着一定的关系。

简谐振动的初相位差是指振动物体在某一时刻与参考点的位移差。

初相位差决定了振动物体的起始位置，它与振动物体的初始条件有关。

初相位差的不同会导致振动物体的运动规律发生变化。

简谐振动的运动方程可以通过牛顿定律和胡克定律推导得到。

牛顿定律指出，物体的加速度与作用在物体上的合外力成正比，胡克定律则描述了弹簧的弹性特性。

将这两个定律结合起来，可以得到简谐振动的运动方程。

简谐振动在自然界和工程中都有广泛的应用。

在自然界中，摆钟的摆动、弹簧振子的弹动、声波的传播等都是简谐振动。

在工程领域中，简谐振动的原理被应用于建筑物的抗震设计、机械振动的控制、电路中的振荡电流等。

简谐振动还有一些特殊的性质。

例如，简谐振动的位移、速度和加速度之间存在着一定的相位关系。

位移和速度的相位差是π/2，位移和加速度的相位差是π。

这些相位关系可以通过简谐振动的运动方程进行推导得到。

简谐振动是物理学中一种重要的振动形式，它可以用运动方程来描述振动物体的运动规律。

简谐振动与波动简谐振动和波动是物理学中两个重要的概念。

简谐振动是指一个物体以固定的频率在一个平衡位置周围做往复运动，而波动则是指能量以波的形式传播的现象。

虽然它们有一些相似之处，但是它们在定义、特点和应用等方面也有一些不同之处。

一、简谐振动简谐振动是指一个物体在一个平衡位置附近做往复运动的现象。

它的特点是振动周期固定，且在平衡位置处的加速度与离平衡位置的距离成正比。

例如，一个挂在弹簧上的质点，在没有外力作用下会以固定的频率上下振动。

简谐振动的周期T和频率f之间有如下关系：T=1/f。

简谐振动还有一个重要的特点是它的运动方程是一个正弦函数。

设x为质点相对平衡位置的位移，t为时间，A为振幅，ω为角频率，则简谐振动的运动方程可以表示为：x=Acos(ωt+φ)，其中φ为初相位。

简谐振动在物理学中有广泛的应用，例如钟摆的运动、声波的传播以及电磁波的振荡等，都可以通过简谐振动来进行描述和解释。

二、波动波动是指能量以波的形式传播的现象。

波动可以分为机械波和电磁波两种类型。

机械波是指需要介质才能传播的波动，例如水波和声波；而电磁波则是不需要介质就能传播的波动，例如光波和无线电波。

波动的特点之一是它的能量传播方向与波传播方向垂直。

例如，水波在向前传播时，水分子的振动方向是垂直于波的传播方向的。

此外，波动还具有反射、折射、干涉和衍射等现象。

波动可以用波函数来描述。

对于机械波，它的波函数可以表示为y(x,t)=Asin(kx-ωt+φ)，其中y为波的振幅，x为波的位置，t为时间，A为振幅，k为波数，ω为角频率，φ为初相位。

波动是物理学中一个广泛研究的领域，它不仅涉及到声波、光波等常见的波动现象，还涉及到其他一些特殊的波动，例如量子波动和粒子波动等。

三、简谐振动与波动的关系简谐振动和波动虽然是两个不同的概念，但它们之间存在着一定的联系。

事实上，简谐振动可以看作是一种特殊的波动现象。

从数学表达上看，简谐振动的运动方程和波动的波函数非常相似，都具有正弦函数形式。

简谐振动特征方程简谐振动是物理学中一个重要的概念，它描述了许多自然界中的现象，例如弹簧振子、摆钟等等。

简谐振动的特征方程是用来描述振动系统的运动规律的，下面我们来详细介绍一下。

简谐振动是指一个物体在一个平衡位置附近做往复运动的现象。

这个物体可以是一个质点、一个弹簧振子、一个摆钟等等。

这些物体在平衡位置附近的运动可以用一个数学模型来描述，即简谐振动的特征方程。

简谐振动的特征方程可以写成如下的形式：m * a + k * x = 0其中，m是物体的质量，a是物体的加速度，k是振动系统的劲度系数，x是物体的位移。

这个方程描述了物体在振动过程中的运动规律。

我们可以从这个方程中得到一些重要的结论。

首先，当物体的位移为0时，即物体处于平衡位置时，方程变为0 = 0，这意味着物体处于静止状态。

其次，当物体受到外力作用时，例如一个弹簧的拉力或一个摆钟的重力，方程变为m * a + k * x = F，其中F是外力。

这意味着物体在外力作用下会发生加速度，从而产生振动。

根据简谐振动的特征方程，我们可以推导出振动系统的运动方程。

假设物体在t时刻的位移为x(t)，速度为v(t)，加速度为a(t)，则有以下关系：x(t) = A * cos(ωt + φ)v(t) = -A * ω * sin(ωt + φ)a(t) = -A * ω^2 * cos(ωt + φ)其中，A是振幅，表示物体的最大位移；ω是角频率，表示物体在单位时间内完成的振动周期数；φ是初相位，表示物体在t=0时刻的相位。

从上面的方程可以看出，简谐振动的运动是周期性的，物体在单位时间内完成的振动周期数是固定的。

振幅决定了物体振动的幅度大小，角频率决定了物体振动的快慢，初相位决定了物体振动的起始位置。

简谐振动的特征方程不仅仅在物理学中有重要的应用，还在其他领域中有广泛的应用。

例如在工程学中，简谐振动的特征方程可以用来描述机械振动系统的运动规律，从而帮助工程师设计和优化振动系统。

简谐运动位移公式推导简谐运动是一种最简单的周期性运动，它的位移与时间之间存在直接的数学关系。

简谐运动的位移公式可以通过对运动的力学特征进行分析和推导得到，下面是一个详细的推导过程：我们假设一个质点进行简谐振动，其位移方程为：y = A sin(ωt + φ)其中，y表示位移，A为振幅，ω为角频率，t为时间，φ为初相位。

简谐振动的特点是周期性和恢复性，即质点在其中一位置不受力的作用时会产生恢复力，使其回到平衡位置。

根据牛顿第二定律，可以得到简谐振动的运动方程：F=ma=-ky其中，F表示作用在质点上的恢复力，m为质点的质量，a为加速度，k为恢复力系数（弹簧的劲度系数）。

根据运动学的关系a = d²y/dt²，将这个等式代入上面的运动方程，我们可以得到：m d²y/dt² = -k y这是一个二阶线性常微分方程，我们假设解为 y = e^(rt)（其中，e为自然对数的底，r为待定常数）。

将这个解代入上面的微分方程，我们可以得到：m r²e^(rt) = -k e^(rt)化简后得到：mr²+k=0此方程是一个关于未知数r的二次方程，解得r₁=i√(k/m)和r₂=-i√(k/m)（其中，i表示虚数单位）。

由于解是复数，因此位移方程需要包含复数的情况，而实际情况下位移是一个实数。

根据欧拉恒等式，我们可以将虚数表示为余弦与正弦的复合形式：e^(ix) = cos(x) + i sin(x)将任意一个解r代入上式，我们可以得到：e^(irt) = cos(√(k/m)t) + i sin(√(k/m)t)由于位移为实数，我们只关注上式中的实部：y = A e^(irt) = A cos(√(k/m)t)此时，y即为简谐振动的位移公式。

其中，A为振幅，√(k/m)为角频率，t为时间。

最后，我们还可以推导出简谐振动的速度和加速度的公式。

根据上面的位移公式，可以求出速度 v = dy/dt 和加速度a = d²y/dt²，分别对时间t求导即可得到：v = d/dt (A cos(√(k/m)t)) = -A√(k/m) sin(√(k/m)t)a = d²/dt² (A cos(√(k/m)t)) = -A(√(k/m))² cos(√(k/m)t)所以，简谐振动的位移、速度和加速度公式分别为：y = A cos(√(k/m)t)v = -A√(k/m) sin(√(k/m)t)a = -A(√(k/m))² cos(√(k/m)t)通过上述推导过程，我们得到了简谐振动的位移、速度和加速度公式，以及位移公式的推导过程。

简谐振动振幅公式
简谐运动振幅公式：x=Asin√k/m)t，简谐运动是最基本也最简单的机械振动，当某物体进行简谐运动时，物体所受的力跟位移成正比，并且总是指向平衡位置。

它是一种由自身系统性质决定的周期性运动，如单摆运动和弹簧振子运动，实际上简谐振动就是正弦振动。

根据该运动方程式，我们可以说位移是时间t的正弦或余弦函数的运动是简谐运动。

简谐运动的数学模型是一个线性常系数常微分方程，这样的振动系统称为线性系统。

线性系统是振动系统最简单最普遍的数学模型。

但一般情况下，线性系统只是振动系统在小振幅条件下的近似模型。

简谐运动的运动方程1. 简谐运动的概念简谐运动是指一个物体在恢复力作用下，在一个固定轴线上进行往复运动的运动形式。

在简谐运动中，物体的加速度与其位移成正比，且方向相反，符合以下的运动规律：1.加速度与位移成正比：a ∝ x2.加速度与位移的符号相反：a = -ω²x3.加速度与时间的关系：a = -ω²A sin(ωt)其中，a表示物体的加速度，x表示物体的位移，A表示运动的幅度（即最大位移），ω表示角频率，t表示时间。

简谐运动可以描述许多真实世界中的现象，如弹簧振子的运动、钟摆的摆动、音叉的振动等。

2. 简谐运动的运动方程简谐运动的运动方程描述了物体在简谐运动中的时间变化规律。

对于简谐运动，其运动方程一般可以表示为：x(t) = A sin(ωt + ϕ)其中，x(t)表示时间t时刻物体的位移，A表示运动的幅度（即最大位移），ω表示角频率，ϕ表示相位角。

•位移：位移x(t)表示物体从平衡位置开始的偏离程度。

•幅度：幅度A表示物体在简谐运动中的最大位移。

•角频率：角频率ω表示单位时间内物体通过一个完整振动周期的次数。

•相位角：相位角ϕ表示物体在t = 0时刻的位移相位。

3. 简谐运动的基本特点简谐运动具有以下的基本特点：3.1 周期性简谐运动是周期性的，物体的位移和速度随时间循环变化，周期T表示物体完成一个完整振动的所需时间。

3.2 能量守恒在简谐运动中，物体的动能和势能之和保持不变，即总机械能守恒。

3.3 相位关系简谐运动中，不同物体的位移之间存在相位差，相位差决定了物体之间的相对位置关系。

4. 简谐运动的重要应用简谐运动有许多重要的应用，下面介绍其中几个应用：4.1 时钟时钟中的摆锤进行来回振荡的运动就是简谐运动。

通过控制摆锤的长度，可以调整时钟的时间精准度。

4.2 天体运动天体运动中的一些周期性现象，如行星的公转运动、恒星的振动等，都可以使用简谐运动来描述。

4.3 电磁波电磁波是一种振动，可以用简谐运动来描述。

能量守恒推导简谐运动方程
我们要从能量守恒的角度推导简谐运动的方程。

首先，我们需要理解简谐运动的基本性质和能量守恒的概念。

简谐运动是一个周期性的运动，其运动方程可以表示为：
x(t) = A × sin(ωt + φ)
其中，A 是振幅，ω是角频率，φ是初相。

在简谐运动中，系统的动能和势能是相互转化的。

动能 E_k = 1/2 × m × v^2 = 1/2 × m × (d/dt(x))^ 2
势能 E_p = k × x^2 / 2
由于简谐运动中动能和势能是相互转化的，所以他们的和是恒定的。

这意味着 d/dt(E_k + E_p) = 0
现在我们要来解这个方程，找出 x(t) 的表达式。

计算结果为：x(t) = A × sin(ωt + φ)
其中，A = sqrt(k/m)，ω = sqrt(k/m)，φ是初相。

所以，从能量守恒的角度，我们成功推导出了简谐运动的方程。