当前位置：文档之家 › 简谐振动动力学方程推导

简谐振动动力学方程推导

  • 格式：docx
  • 大小：25.21 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

谐振子

谐振子

O
2) 由： A
02
2 0
和已知条件：
2
0
x0
b
x0
mg k
0.05
m
b
O' 0
x0
可得：A 0.07 m
x
3)
由
tg 0
0 0
1
和初速度为负值，可知：0 4
4) (t) Acos(t ) 0.07cos(4t 4) (m)
5) E 1 kA2 0.039 (J) 6) 做图略
x0
和速度
0，由：
x0
Acos Asin
0
联立可得：
A
x02
2 0
2
tg1( 0 ) x0
简谐运动实例：
( 1 ) 单摆
准弹性力：
l
1. 细线质量不计 约
ft mg
定 2. <5 以保证sin 由牛顿定律：
m
ft
3. 阻力忽略不计
ft
பைடு நூலகம்
mg
mat
m
l
ml
d2
dt 2
mg
d2g 0
dt2 l
一个作简谐运动的质点所受的沿位移方向的合外力 与它对于平衡位置的位移成正比而反向。这样的力称为 恢复力(Restoring Forces)。
2. 动力学方程 (以水平弹簧振子为例)
由 f ma m d2 x dt2
及 f kx 得
f
k
m
0x
x
弹簧振子
d2 x m d t 2 kx
d 2x dt2
§4.2 谐振子(动力学部分) (Harmonic Oscillator)

简谐振动的能量、单摆和复摆

简谐振动的能量、单摆和复摆

简谐运动能量图
o
能量
x−t
T
ϕ =0 t x = A cosωt v − t v = − Aω sin ω t
1 E = kA 2 2 1 2 2 E p = kA cos ω t 2
o
T 4
T 2
3T 4
T
t
1 2 2 2 Ek = mω A sin ωt 2
（33）简谐振动的能量、单摆和复摆 33）简谐振动的能量、
− 2A/ 2
2 x1 = ± A 2
O
2A/ 2
x
x1 = ±7.07×10 m
−3
（33）简谐振动的能量、单摆和复摆 33）简谐振动的能量、
机械振动
（5）当物体的位移为振幅的一半时动能、势能 ）当物体的位移为振幅的一半时动能、 各占总能量的多少? 各占总能量的多少
1 2 1 A E Ep = kx = k = 2 2 2 4
ω = k /m
1 2 2 （振幅的动力学意义） E = Ek + Ep = kA ∝ A 振幅的动力学意义） 2
线性回复力是保守力， 简谐运动的系统机械能守恒 线性回复力是保守力，作简谐运动的系统机械能守恒 保守力 运动的系统
（33）简谐振动的能量、单摆和复摆 33）简谐振动的能量、
机械振动
x, v
（33）简谐振动的能量、单摆和复摆 33）简谐振动的能量、
（3）总能量； ）总能量；
机械振动
E = Ek ,max= 2.0 × 10 J
（4）物体在何处其动能和势能相等？ ）物体在何处其动能和势能相等？
−3
Ep1 = Ek1 = =
E 2
kA2 4
Ep1 = kx

谐振动的运动学

谐振动的运动学

)
令 t=0 则
x0
A c os 0
(1)
V 0
Asin 0
(2)
12 22
得
A
x02
V02
2
2、周期T（频率、圆频率ω 、固有圆频率）
（1）周期T：完成一次完全振动所需的时间
x Acos(t 0 ) Acos(t T ) 0
Acos(t 0 2 )
T 2
或 T 2
2
(2)频率：单位时间内所完成的完全振动的次数
13
2、参考圆、参考点：
(1) 所谓参考圆：指旋转矢量旋转一周时矢量端点的轨迹；而矢量的端点则谓之参 考点。
参考点在坐标轴上的投影才是谐振动。
（2）利用参考点在参考圆中的位置来判断振动位相所在的象限
由图可知:
x>0, v<0 , φ在第 I 象限
v2
v1
x<0, v<0 , φ在第Ⅱ 象限 x<0, v>0 , φ在第 III 象限 x>0, v>0 , φ在第Ⅳ 象限
φ ＝tg-1（－ｖ0／ωｘ0）＝12.6° 在第三象限， φ0 ＝180°＋12.6°
或取
φ0 ＝180°+12.6°＝192.6°＝3.36 rad
也可写成 φ0 ＝－2.92 rad
振动表达式为
ｘ＝2.05×10-2cos（11.2ｔ－2.92） （ＳＩ）
12
三、谐振动的旋转矢量表示法
1、旋转矢量的规定法则 (1) 旋转矢量的制作
两个同频振动在同一时刻的位相之差
Δφ=φ20-φ10
2）同一振动在不同时刻的位相差
同一振动在t1、t2时刻的位相差为
Δφ=(ωt2+φ0)-(ωt1+φ0)=ω(t2-t1)

振动方程简.ppt

振动方程简.ppt

解：1) 首先确定三个物理量ω, A, φ.
x Acos(t )
x
A
A/2
a
o
-A
Tt
振动曲线
已知A, T, ω=2π/T, 如何求φ？ 方法1：解析法
将t=0, x0=A/2， t>0, v = -Aωsinφ>0代入方程
17
x A A/2
a
o
-A
cos 1
2
t Asin 0
3
T
代t 入 方
2. 周期、频率:
1
T 2π
x xt图
A
o
Tt
T
A
2
圆频率 2v 2
T
周期和频率仅与振动系 统本身的物理性质有关
弹簧振子周期
T 2π m k
6
3. 相位 t
相 位 (t) t
相位的意义：决定任意时刻物体的运动状态
1)相差 2nπ (n为整数)质点运动状态相同.
2）初相位 (t 0) 描述质点初始时刻的运动状态.
3
O
A x t 1 (s) 0.13s
18
v
x/m
0.05 0.025 o 0.025 0.05
15
3）若物体在x=0.05 m处时速度不为0，而是具有 向右的初速度v0=0.30 m•s-1 ，求其运动方程。
解：A和φ由初始条件x0 = 0.05m, v0 = 0.30 m•s-1定
O
1 2
kA2
1 2
kx02
1 2
m v02
A2
x02
m k
v02
2 k , k m2
m
A
x02
v02

简谐振动的方程

简谐振动的方程

m
O
x X
k mg / l
令向下有位移x, 则 f mg k (l x) kx
作谐振动
设振动方程为

x A cos(t 0 )
k m g l 9.8 10rad / s 0.098
由初条件得
A x0 (
2
v0

) 2 0.098m
0 是t =0时刻的位相—初位相
(4)简谐振动的旋转矢量表示法

A
t
t t

t0
o
x
x
x A cos(t )
请看动画……
用旋转矢量图画简谐运动的 x t 图
三 简谐运动的特征
1）
2） 3）
F kx
d2 x 2 x 2 dt
(平衡位置
x0 )
v0 0 arctg ( ) 0, x0
由x0=Acos0=-0.098<0 cos0<0, 取0= 振动方程为：x=9.810-2cos(10t+)m
(2)按题意 t=0 时
m
O
x X
x0=0，v0>0
x0=Acos0=0 , cos0=0 0=/2 ,3/2 v0=-Asin>0 , sin 0 <0, 取0=3/2 x=9.810-2cos(10t+3/2) m
x t 图
x A cos t
x
A
t
v t 图
v A sin t
A cos(t
A

2 )
2
v
t
a t 图
a A 2 cos t

简 谐 振 动

简 谐 振 动
周期、频率和角频率都是描述物体振动快慢的物理量。在
国际单位制中，周期的单位为秒（s）；频率的单位为赫兹 （Hz）；角频率的单位为弧度每秒（rad/s）。
对弹簧振子，由于
k
m
故有：
T 2π m k
1 k
2π m
由上式可以看出，弹簧振子的周期和频率都是由物体的质量 m和弹簧的劲度系数k所决定的，即只与振动系统本身的物理性 质有关。因此，我们将这种由振动系统本身的性质所决定的周期 和频率称为固有周期和固有频率。
v dx Asin（t ）
dt
a
d2x dt 2
2 Acos（t
）
【例10-1】如下图所示，一质量为m、长度为l的均质细棒 悬挂在水平轴O点。开始时，棒在垂直位置OO′，处于平衡状态。 将棒拉开微小角度θ后放手，棒将在重力矩作用下，绕O点在竖 直平面内来回摆动。此装置是最简单的物理摆，又称为复摆。 若不计棒与轴的摩擦力和空气阻力，棒将摆动不止。试证明在 摆角很小的情况下，细棒的摆动为简谐振动。
由胡克定律可知，在弹性限度内，物体受到的弹力F的大小 与其相对平衡位置的位移x成正比，即F＝－kx
上式中，负号表示弹力的方向与位移的方向相反，始终指向 平衡位置，因此，此力又称为回复力。
根据牛顿第二定律可知，物体的加速度为：
a F k x mm
因k和m都是正值，其比值可用一个常数ω的平方表示，即ω2 ＝k/m，故上式可写为：
物理学
简谐振动
物体运动时，如果离开平衡位置的位移（或角位移）按余 弦函数或正弦函数的规律随时间变化，则这种运动称为简谐振 动。在忽略阻力的情况下，弹簧振子的振动及单摆的小角度摆 动等都可视为简谐振动。
1.1 简谐振动的运动方程
如下图所示，一轻弹簧（质量可忽略不计）放置在光滑水平 面上，一端固定，另一端连一质量为m的物体。这样的系统称为 弹簧振子，它是物理学中的又一理想模型。

简谐振动方程

简谐振动方程
简谐振动的方程
一、简谐振动的动力学方程
1.弹簧振子
l0 k
m
d2x m dt2
F
kx
A o
x
A
k 2
m
d2x k
dt 2
m
x0
d2 dt
x
2
2
x
0
(1)
2 单摆
sin
(ml
2
)
d2
dt 2
M mgl
d2
dt 2
g l
0
(2)
记 2 g x
l
d2x dt 2
2x
0
(1)
O
l
T
mg
mg k
1
1
(m
2kh M
)g
一、简谐振动的动力学方程
小
d2 dt
x
2
2
x
0
结
二、简谐振动的运动学方程
x Acos(t )
t t A
t
t 0 x
o
x
x Acos(t )
旋转矢量法
初始条件确定A 初位相
例:如图m=2×10-2kg,弹簧的静止形变为l=9.8 cm. t=0 时,x0=-9.8cm,v0=0
2 描述简谐振动的特征量
(1)振幅 A
x Acos(t )
(2)周期、频率、圆频率
弹簧振子 k
m
单 摆 g
l
T 2 m
k
T 2 l
g
1 k 2 m
1 g 2 l
复 摆 mgh T 2 I 1 mgh
I
mgh
2 I
(3) 位相和初位相
x A cos(t 0 )

机械振动——简谐运动的基本概念

机械振动——简谐运动的基本概念
f=-kx
式中的比例系数k为弹簧的劲度系数（Stiffness），它反映弹簧的固有性质，负号表示力的方向与位移的方向相反，它是始终指向平衡位置的。离平衡位置越远，力越大；在平衡位置力为零，物体由于惯性继续运动。这种始终指向平衡位置的力称为回复力。
2．动力学方程及其解
根据牛顿第二定律，
f=ma
可得物体的加速度为
对于给定的弹簧振子，m和k均为正值常量，令
则上动的微分方程。
三、简谐运动的运动学特征：
1．简谐振动的表达式（运动学方程）
简谐运动的微分方程的解具有正弦、余弦函数或指数形式。我们采用余弦函数形式，即
这就是简谐运动的运动学方程，式中A和φ是积分常数。
说明：
1）简谐运动不仅是周期性的，而且是有界的，只有正弦函数、余弦函数或它们的组合才具有这种性质，这里我们采用余弦函数。
定义：物体在2π秒时间内所作的完全振动的次数，用ω表示，单位为弧度/秒(rad. s-1或s-1)。
说明：
1）简谐运动的基本特性是它的周期性；
2）周期、频率或圆频率均有振动系统本身的性质所决定，故称之为固有周期、固有频率或固有圆频率。
3）对于弹簧振子， ， ， 。
4）简谐运动的表达式可以表示为
三、相位(Phase)—反映振动的状态
物体在B、C之间来回往复运动。
结论：物体作简谐运动的条件：
物体的惯性——阻止系统停留在平衡位置
作用在物体上的弹性力——驱使系统回复到平衡位置
二、弹簧振子的动力学特征：
1．线性回复力
分析弹簧振子的受力情况。取平衡位置O点为坐标原点，水平向右为X轴的正方向。由胡克定律可知，物体m(可视为质点)在坐标为x(即相对于O点的位移)的位置时所受弹簧的作用力为

简谐运动的表达式动力学表达式

简谐运动的表达式动力学表达式

性势能各是怎样变化的？
（3）该振子在前100 s的总位移是多少？路程是
多少？
精品
思维导图
解析 （1）由振动图象可得 A=5 cm,T=4 s, =0
则ω= 2 =π rπad/s
T2
故该振子简谐运动的表达式为 x=5 sin tπ cm
2
精品
(2)由图可知,在t=2 s时,振子恰好通过平衡位
置,此时加速度为零,随着时间的延续,位移值不
摆球重力沿与摆线 弹簧的弹力提供 垂直（即切向）方
向的分力
精品
周期公式
m
T=2π k (不作要求)
T=2π
l g
能量转化
弹性势能与动 重 力 势 能 与
能 的 相 互 转 化 ，动 能 的 相 互 机 械 能 守 转化，机械能
恒
守恒
精品
三、受迫振动和共振
1.受迫振动：物体在 周期性驱动力 作用下的振动.
4
大，这时速度为零.由此可见，丙的速度变化正 好对应甲的位移变化情况.所以A正确.同样可推 出B正确，C、D不正确. 答案 AB
精品
题型2 简谐运动图象的应用
【例2】如图6为一弹簧振子的振动图象,试完成以
下要求：
（1）写出该振子简谐运动的
表达式.
（2）在第2 s末到第3 s末这
图6
段时间内弹簧振子的加速度、速度、动能和弹
零
零
T 2
零
零 负向 最大 正向 最大
3T 4
负向 最大 正向 最大
零
零
T
零
零 正向 最大 负向 最大
精品
A.若甲表示位移x,则丙表示相应的速度v B.若丁表示位移x,则甲表示相应的速度v C.若丙表示位移x,则甲表示相应的速度v D.若乙表示位移x,则丙表示相应的速度v 解析 当t=0时，甲的位移为零，这时刻的速度 为正向最大；当t= 1 T时，甲的位移为正向最

简谐振动的动力学方程

简谐振动的动力学方程


1 T
t T
Ek dt
t
1 kA2 4
E P

1 T
t T

E dt P
t

1 kA2 4
(3) 机械能
E

Ek

Ep

1 kA2 2
简谐振动系统 机械能守恒
(3) 机械能
E

Ek

Ep

1 kA2 2
弹簧振子总的机械能和振幅的平方成正比， 这一结论对其它的简谐振动系统也是正确的， 从能量的角度看振幅不仅反映振动的幅度， 还反映振动的强度
k max
2
k min
P max
2
P min
1 KA2 2
o
EE
P
K
x
E
E E
K
P
t
E 1 kA2 sin 2 ( t )
K
2
E 1 kA2 cos2 ( t )
P
2
E
1 kA2 , E
0
k max
2
k min
E
1 kA2 , E
0
P max
2
P min
Ek
O
l
m o
t 时刻细绳与竖直方向
夹角为θ
忽略空气阻力，
小球受力如图.
小球所受合外力矩为

M M M
T
G
选择逆时针方向为正
●
l
T
o mg
M mgl sin
M 0 T
M mgl sin G
M mgl sin
由转动定律 d 2
M J dt 2

弹簧振子作简谐振动的动力学方程

弹簧振子作简谐振动的动力学方程
dv d ˆ : mg sin ma m ml ml dt dt
2 v ˆ : T mg cos m n
l
若 很小，则近似： sin
因此，
,则： l g
l 0 g
（ 2）
ˆ n
2 0， 2 0 0
6
§9.2 简谐振动的运动学
一、简谐振动的运动学方程
d2x 2 方程 0 0 的解为： 2 dt
x A cos( 0 t )
（1）
上式就是简谐振动的运动学方程，该式又是周期函数， 故简谐振动是围绕平衡位置的周期运动。
7
二、描述简谐振动的物理量
1. 周期（T）
完成一次全振动所用的时间：
T
2

对弹簧振子：
k T 2 m
2
） 2. 频率（
单位时间内完成的全振动的次数：
的含义： 2
1 T 2
2
个单位时间内完成的全振动的次数，即圆频率。
8
3. 振幅
定义：物体离开平衡位置的最大位移。
x 振幅可以由初始条件决定。如：t =0时刻，
由⑴式可得：
2x 0 x
（ 1）
2
2x 0 x
（1）
弹簧振子作简谐振动的动力学方程。
总结：
2 0 如质点运动的动力学方程可归结为： x x 0 的形式，且其中 0 决
定于振动系统本身的性质。⑴式的形式就是简谐振动的动力学方程式。
3
2. 单摆
ˆ) ˆ ( , n 建立自然坐标系：
当 t 0 时， 叫初相位。
由：
x A cos( 0 t ) A cos v A 0 sin( 0 t ) A 0 sin

简谐运动的动力学方程

简谐运动的动力学方程
在振动过程中, 物体所受到的合外力与其相对于平衡位 置的位移成正比而反向(始终指向平衡位置), 这样的力称为 线性恢复力.
简谐运动的动力学方程
由牛顿第二定律
m d 2x kx dt2
或
d2x k x 0
dt2 m
令
2 k
m
得
d2x2 x 0
dt2
—简谐运动动力学方程
微分方程的解为 x Acos(t)
(1)单摆
如图, 细线的上端固定, 另一 端悬挂一可看作质点, 质量为 m 的重物, 细线的质量和伸长可忽 略不计. 这一振动系统叫做单摆. 重物叫做摆球, 细线叫做摆线.
若把摆球从平衡位置略为拉 开后放手, 摆球就在竖直平面内 来回摆动.
解: 规定: 右方顺时针 > 0 左方逆时针 < 0
在忽略空气阻力的情况下, 合外力沿 切线方向的分力(即重力分力) 为
它拉开一个微小角度 θ后释放. 若忽
略阻力和摩擦力, 则物体将绕轴 O作微 小的自由摆动. 这样的装置叫做复摆.
简谐运动的动力学方程
简谐运动的动力学方程
解: 复摆在力矩 M的作用下的作用下的作用下的作用下,,由
定定轴律转动定M律由m定g轴l转J动定d律2由定轴转动定律由定轴转动
dt2
动力学方程为 d2 mgl
Fτ mgsin
切向运动方程为
mgsin maτ ml
d2
dt2
即
d2 g sin 0
dt2 l
为非简谐运动.
简谐运动的动力学方程
Fτ
当θ很小时 < 50 0.0873rad sin
为简谐运动 d22
dt2
0
单摆的角频率和周期分别为

简谐振动的运动学方程

简谐振动的运动学方程

简谐振动的运动学方程一、简谐振动的概念和特征简谐振动是指在没有阻力的情况下，一个物体围绕着平衡位置做往复运动的现象。

简谐振动具有以下特征： - 循环性：振动物体围绕平衡位置做往复运动，一次完整的运动称为一个循环。

- 周期性：振动物体完成一个循环所需的时间称为振动的周期，记为T。

- 频率性：振动的频率是指单位时间内完成的循环数，记为f，与周期的倒数成正比。

二、简谐振动的描述简谐振动的运动学方程用来描述振动物体位置随时间的变化关系。

对于单摆、弹簧振子等简谐振动系统，可以根据其运动状态和受力情况建立相应的方程。

2.1 单摆的简谐振动单摆的简谐振动是指将一个质点用一根轻细线连接到固定点上，质点在重力作用下围绕该固定点做往复运动的现象。

单摆的运动学方程可以通过下面的推导得到：•设单摆的质点离开平衡位置的角度为θ，质点到固定点的距离为l。

•考虑到单摆的往复运动，可将角度θ表示为θ = θ0sin(ωt + φ)，其中θ0为最大摆角，ω为角速度，t为时间，φ为相位角。

•根据几何关系可知，质点在水平方向上的位移为l sinθ，根据物体在一维直线运动中的位移与时间的关系，可得到质点在水平方向上的位移与时间的关系方程为x = l sin(θ0sin(ωt + φ))。

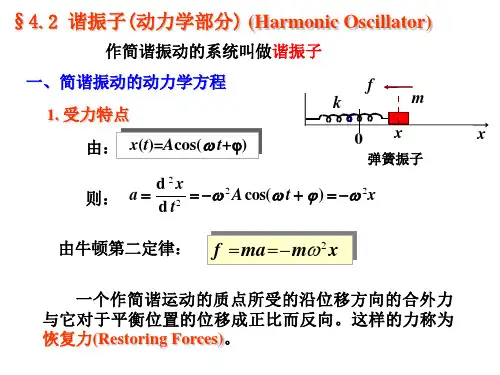
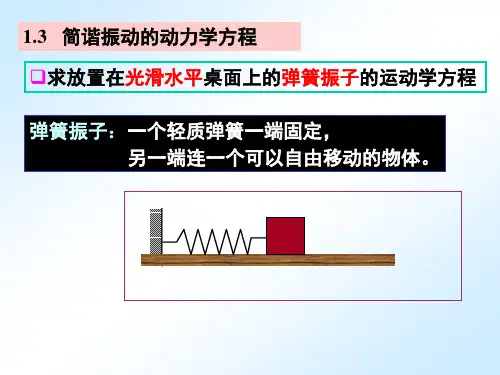
2.2 弹簧振子的简谐振动弹簧振子是指将一根具有一定弹性的弹簧的一端固定，另一端挂上质点后产生的简谐振动现象。

弹簧振子的运动学方程可以通过下面的推导得到：•设弹簧振子的质点离开平衡位置的位移为x，弹簧的劲度系数为k，质点的质量为m。

•根据胡克定律可知，弹簧的拉力与位移成正比，即F = -kx。

•根据牛顿第二定律可知，质点所受的合力与加速度成正比，即F = ma。

•将上述两个等式联立可得到弹簧振子的运动学方程为m*d2x/dt2 + kx = 0。

三、求解简谐振动的运动学方程为了求解简谐振动的运动学方程，我们需要确定简谐振动的周期、频率和振幅。

借助初态条件和边界条件，我们可以使用微分方程求解的方法得到简谐振动的解析解。

简谐振动的运动方程

简谐振动的运动方程

设振动的周期为T，周期函数满足 x(t T ) x(t)
引入 2
T
称为基频率，简称基频
n n次谐频（n = 2为二次谐频，其它依此类推）
14
傅里叶级数： 1, cost, sint, cos2t, sin 2t, cosnt, sin nt,
它们都具有周期 T，且有正交性和完备性
0
Bn

2 T
T
x(t)sin ntdt
2
0
n
19
x(t)

2


sin
t

1 2
sin
2t

1 3
sin
3t


20
非周期性振动的傅里叶分解
非周期性的振动，可理解成T →ω的周期振动，基频ω→0， 分解出的简谐振动频率间距ω→0 ，对应的振动频谱是连续谱。
简谐振动的复数表示法 Acos(t ) Aei(t)
多普勒效应探测器所接受到的波的频率依赖于波源和探测器相对介质的运动在无色散的介质中波速与波源和探测器的运动与否无关波源频率探测器1波源静止观察者运动波源波速u探测器先讨论波源或探测器的运动都在二者的连线上波相对观察者的传播速度波长未变观察者感受到的频率2波源运动观察者静止波源波速u探测器波相对观察者的有效波长波速未变观察者感受到的频率3波源和观察者都运动波源波速u探测器波相对观察者的有效波长观察者感受到的频率波相对观察者的传播速度波源和观察者作任意运动波源观察者相位增量观测到同样的相位增量波源观察者声速车速声音经前面墙的反射向后传播求人听到的拍频
解得
A 2a0
tan 1 / 4 or / 4
考虑到 sin a0 / A 0 /4

2简谐振动的动力学方程

2简谐振动的动力学方程

g l
dengyonghe1@
例4.3 复摆
M = − m g l sinθ ≈ − m g l θ
据 M =Iβ =I − mg lθ = I d 2θ d 2θ dt
2
o
d 2θ dt
2
得
θ
c
整理得
mg
mgl mgl + θ =0 记 =ω2 I I d t2 d 2θ d t2 + ω 2θ = 0
I T= = 2π mgl ω 2π

单摆？
I = ml 2
T = 2π
l g
dengyonghe1@
LC电路：如图 电路： 电路 当开关K接向 时达到稳定 当开关 接向b时达到稳定， 接向 时达到稳定， 在电容器内储存了能量. 在电容器内储存了能量 当开关K接向 时 当开关 接向c时，由于电容 接向 器内储存了能量，会对LC回 器内储存了能量，会对 回 路放电，电流为i，即： 路放电，电流为 ，
2
F = ma = −mω x
2
在位移方向的合外力与它对平衡位置的位移成正比且反向。 在位移方向的合外力与它对平衡位置的位移成正比且反向。
即：
F = − kx
2
d x m 2 = −kx dt
常系数二阶微分方程
dengyonghe1@
2
d x k + x=0 2 dt m
d x k k 2 + x=0 令ω = 2 m dt m 可以确定方程的解： 由初始条件x(t = o), v(t = 0)可以确定方程的解：
2 E0 A= k
振幅取决于振动的总能量
dengyonghe1@
单摆： 质量集中于小球上， 单摆： 质量集中于小球上， 不计悬线质量。 不计悬线质量。 取逆时针为 θ 张角正向， 张角正向， 以悬点为轴，受力如图。 以悬点为轴，受力如图。 只受到切方向的合外力： 只受到切方向的合外力：

简谐振动运动方程的推导

简谐振动运动方程的推导

2E mgL
Cos (
g L
t+
U0)
令 A= m2gEL, X= 单摆的运动方程
g L
代入(
13
)
式可得到
H= ACos( Xt + U0) 的形式.
2 应用牛顿第二运动定律
2. 1 弹簧振子:
物体 m 总是受到 回复力 f 的作用, 根据胡
克定律及牛顿第二运动定律得-
kx=
m
d2x dt2
,
并
设 X2=
210. [ 4] 马文蔚. 柯 景凤. 物 理学[ M] . 下册. 北 京: 高等 教
育出版社, 1982. 1- 18. [ 5] 刘克哲. 普通物理学[ M] . 北京: 高等教育 出版社,
1994. 114- 124. [ 6] 祝 之 光. 物理 学 [ M ] . 下 册. 北 京: 高 等 教育 出 版
参考文献: [ 1] 梁绍荣. 刘昌年. 盛正 华. 普 通物理学[ M ] . 第 一分
册. 力学. 北京: 高等教育出版社, 1995. 299- 303. [ 2] 顾 建 中. 力学 教 程[ M] . 北 京: 高 等 教育 出 版社,
1985. 150- 162. [ 3] 孙庆元. 力学 [ M] . 青岛: 海 洋出 版社, 1992. 197-
CAI qun1 LIU Yan2
( Department of Physics, Mengzi T echers. College, Mengzi 661100 China; 2) Department of Physics, Yunnan Normal University, Kunming 650031 China)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

简谐振动动力学方程推导
简谐运动可以看做圆周运动的投影，所以其周期也可以用圆周运动的公式来推导。

圆周运动的；很明显v无法测量到，所以根据得到。

其中向心力F便可以用三角函数转换回复力得到即（F=-kx中负号只表示方向，所以在这省略）。

所以得到；
因为x与r之间的关系是：x=rcosα，所以上式继续化简得
到：。

然后再将v带入之前的圆周运动T中，即可得到。

将R记为匀速圆周运动的半径，即：简谐运动的振幅；
将ω记为匀速圆周运动的角速度，即：简谐运动的圆频率，
则：；
将φ记为 t=0 时匀速圆周运动的物体偏离该直径的角度（逆时针为正方向），即：简谐运动的初相位。

则，在t时刻：
简谐运动的位移x=Rcos（ωt+φ）；
简谐运动的速度v=-ωRsin（ωt+φ）；
简谐运动的加速度a=-ω2Rcos（ωt+φ），上述三式即为简谐运动的方程。