人教B版高中数学必修四高一作业设计：1.2.1三角函数的定义

1．21 任意三角函数的定义（一）
一。

、教学目标
1．知识目标：（1）让学生理解任意角的三角函数的定义；
（2）掌握三角函数（正弦、余弦、正切）的定义域;
(3) .理解并掌握各种三角函数在各象限内的符号.
2．能力目标：（1）培养学生应用图形分析数学问题的能力；
（2）学会运用任意三角函数的定义求相关角的三角函数值；
（3）树立映射观点，正确理解三角函数是以实数为自变量的函数；
（4）判断.三角函数值在各象限内的符号.
3．情感目标：（1）通过网络载体，利用几何画板的直观演示，培养学生主动探索、善于发现的创新意识和创新精神；
（2）在学习过程中通过相互讨论培养学生的团结协作精神；
（3）通过三角函数定义的学习，从中体会三角函数像一般函数一样，具有一
般函数的抽象美。

二、教学重点
（1）任意角的正弦、余弦、正切的定义；
（2）三角函数的定义域；
（3）根据任意角的三角函数定义求三角函数值。

（4）判断.三角函数值在各象限内的符号.
三、教学难点
任意角的正弦、余弦、正切的定义；。

必修四第一章 三角函数1.2.1 三角函数的定义1.若02πα<<－，则点()P tan cos αα，位于( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2.设α角属于第二象限，且||22coscos ππ＝－，则2α角属于( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限3.已知角α的终边过点(－3cos θ，4cos θ)，其中θ∈(2π，π)，则cos α＝________. 4.5sin 90°＋2cos 0°－3sin 270°＋10cos 180°＝__________.5.已知角α的终边上一点的坐标为22sin,cos 33ππ⎛⎫ ⎪⎝⎭，则角α的最小正值为 ( ) A.56π B.23π C.35π D.116π 6.已知角α的顶点在原点上，始边与x 轴正半轴重合，点P (－4m,3m )(m >0)是角α终边上一点，则2sin α＋cos α＝________.7.已知角α的终边在直线y 上，求α的三角函数值．8.已知点534(4)P sin cos ππ，落在角θ的终边上，且θ∈[0,2π)，则θ是第________象限角． A ．一 B ．二C ．三D ．四9.已知角θ的终边上有一点P (x ，－1)(x ≠0)，且tan θ＝－x ，求sin θ，cos θ.10.已知角α终边经过点()(0P x x ≠，且cos x α，求sin α、tan α的值．答案1.选B.2.选C.3.答案：354.答案：05.D6.257.答：tan αsin α＝2 ，cos α＝12，或tan α，sin α＝－2，cos α＝－12. 8．答案：C9.解： 当x ＝1时，sin θ＝－2，cos θ＝2；当x ＝－1时，sin θ＝－2，cos θ＝－2.10.解：sin α＝－6tan α＝5 .。

1．2.1三角函数的定义(1)任意角的三角函数的定义是什么？(2)三角函数值的大小与其终边上的点P的位置是否有关？(3)如何求三角函数的定义域？(4)如何判断三角函数值在各象限内的符号？[新知初探]1．三角函数的定义(1)前提准备：①以角α的顶点O 为坐标原点，以角α的始边的方向作为x 轴的正方向，建立平面直角坐标系xOy ，如图所示．②设角α的终边上任一点P (x ，y )，OP ＝r (r ≠0)． (2)定义：①余弦函数：x r 叫做角α的余弦，记作cos α，即cos α＝xr . ②正弦函数：y r 叫做角α的正弦，记作sin α，即sin α＝yr . ③正切函数：y x 叫做角α的正切，记作tan α，即tan α＝yx .④正割函数：角α的正割sec α＝1cos α＝r x .⑤余割函数：角α的余割csc α＝1sin α＝r y .⑥余切函数：角α的余切cot α＝1tan α＝x y .[点睛] 三角函数也是函数，都是以角为自变量，以单位圆上点的坐标(坐标的比值)为函数值的函数；三角函数值只与角α的大小有关，即由角α的终边位置决定．2．正弦函数、余弦函数和正切函数的定义域3．三角函数值的符号 如图所示：正弦：一二象限正，三四象限负； 余弦：一四象限正，二三象限负； 正切：一三象限正，二四象限负．简记口诀：一全正、二正弦、三正切、四余弦．[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)(1)三角函数也是函数，它们都是以角为自变量的，以比值为函数值的函数．( ) (2)若sin α＝sin β，则α＝β.( )(3)已知α是三角形的内角，则必有sin α>0.( ) 答案：(1)√ (2)× (3)√2．若sin α<0，tan α>0，则α在( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限答案：C3．若角α的终边经过点P (2,3)，则有( ) A ．sin α＝21313 B ．cos α＝132C ．sin α＝31313D ．tan α＝23答案：C4．sin π3＝________，cos 3π4＝________.答案：32 －22[典例] 已知角α的终边经过点P (－4a,3a )(a ≠0)，求sin α，cos α，tan α的值． [解] r ＝(－4a )2＋(3a )2＝5|a |.若a ＞0，则r ＝5a ，故sin α＝y r ＝3a 5a ＝35，cos α＝x r ＝－4a 5a ＝－45，tan α＝y x ＝3a －4a ＝－34.若a ＜0，则r ＝－5a .同理可得sin α＝－35，cos α＝45，tan α＝－34.利用三角函数的定义求值的策略(1)已知角α的终边在直线上求α的三角函数值时，常用的解题方法有以下两种： 法一：先利用直线与单位圆相交，求出交点坐标，然后再利用正、余弦函数的定义求出相应三角函数值．法二：在α的终边上任选一点P (x ，y )，P 到原点的距离为r (r >0)．则sin α＝yr ，cos α＝xr .已知α的终边求α的三角函数值时，用这几个公式更方便．(2)当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．[活学活用]1．设θ是第三象限角，P (－4，y )为其终边上的一点，且sin θ＝16y ，则tan θ等于( )A ．－52B ．－255C.255D.52 解析：选D 因为sin θ＝y(－4)2＋y 2＝16y ， 所以16＋y 2＝6，解得y ＝±25，又θ是第三象限角，所以y ＝－25， 所以tan θ＝－25－4＝52，故选D.2．已知角α的终边落在直线3x ＋y ＝0上，求sin α，cos α，tan α，sec α，csc α，cot α的值．解：直线3x ＋y ＝0，即y ＝－3x ，则直线通过第二和第四象限． ①在第二象限内取直线上的点(－1，3)，则r ＝(－1)2＋(3)2＝2，所以sin α＝32，则csc α＝23＝233； cos α＝－12，则sec α＝－2；tan α＝－3，则cot α＝－33. ②在第四象限内取直线上的点(1，－3)，则r ＝12＋(－3)2＝2，所以sin α＝－32，则csc α＝－233； cos α＝12，则sec α＝2；tan α＝－3，则cot α＝－33.[典例] (1)若角θ同时满足sin θ<0且tan θ<0，则角θ的终边一定位于( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限(2)设α是第三象限角，且⎪⎪⎪⎪cos α2＝－cos α2，则α2所在象限是( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限[解析] (1)由sin θ<0，可知θ的终边可能位于第三或第四象限，也可能与y 轴的负半轴重合．由tan θ<0，可知θ的终边可能位于第二象限或第四象限，故θ的终边只能位于第四象限．(2)∵α是第三象限角， ∴2k π＋π<α<2k π＋3π2，k ∈Z.∴k π＋π2<α2<k π＋3π4, k ∈Z ，∴α2在第二、四象限． 又∵⎪⎪⎪⎪cos α2＝－cos α2，∴cos α2<0.∴α2在第二象限． [答案] (1)D (2)B对于已知角α，判断α的相应三角函数值的符号问题，常依据三角函数的定义，或利用口诀“一全正、二正弦、三正切、四余弦”来处理．[活学活用]1．设△ABC 的三个内角为A ，B ，C ，则下列各组数中有意义且均为正值的是( ) A ．tan A 与cos B B ．cos B 与sin C C ．sin C 与tan AD ．tan A2与sin C解析：选D ∵0＜A ＜π，∴0＜A 2＜π2，∴tan A2＞0；又∵0＜C ＜π，∴sin C ＞0.2．当α为第二象限角时，|sin α|sin α－cos α|cos α|的值是( )A ．1B ．0C ．2D ．－2解析：选C ∵α为第二象限角，∴sin α>0，cos α<0. ∴|sin α|sin α－cosα|cos α|＝sin αsin α－cos α－cos α＝2.求三角函数的定义域[典例] 求函数f (x )＝sin x ＋lg cos xtan x的定义域．[解] 要使f (x )有意义，则⎩⎪⎨⎪⎧sin x ≥0，cos x ＞0，tan x ≠0，x ≠k π＋π2，k ∈Z ，所以⎩⎨⎧2k π≤x ≤2k π＋π，k ∈Z ，2k π－π2＜x ＜2k π＋π2，k ∈Z ，x ≠k π＋π2，x ≠k π，k ∈Z.解得：2k π＜x ＜2k π＋π2，k ∈Z.所以原函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π＜x ＜2k π＋π2，k ∈Z .求三角函数定义域的方法(1)求函数的定义域，就是求使解析式有意义的自变量的取值范围，一般通过解不等式或不等式组求得．对于三角函数的定义域问题，还要考虑三角函数自身定义域的限制．(2)要特别注意求一个固定集合与一个含有无限多段的集合的交集时，可以用取特殊值把不固定的集合写成若干个固定集合再求交集．[活学活用]求下列函数的定义域： (1)y ＝sin x ＋cos xtan x；(2)y ＝cos x ＋－tan x .解：(1)要使函数式有意义，需tan x ≠0，解得x ≠k π(k ∈Z)． 要使tan x 有意义，需x ≠k π＋π2(k ∈Z)，解得x ≠k π2(k ∈Z)．所以函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2，k ∈Z . (2)由题意得⎩⎪⎨⎪⎧cos x ≥0，－tan x ≥0.x ≠π2＋k π，k ∈Z ，由cos x ≥0得x 的终边在y 轴上，或第一象限，或第四象限，或在x 轴非负半轴上． 由－tan x ≥0，得tan x ≤0，则角x 的终边在第二象限，或第四象限，或在x 轴上． 综上，角x 的终边在第四象限或x 轴非负半轴上．所以函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪－π2＋2k π＜x ≤2k π，k ∈Z .层级一 学业水平达标1．若α＝2π3，则α的终边与圆x 2＋y 2＝1的交点P 的坐标是( ) A.⎝⎛⎭⎫12，32 B.⎝⎛⎭⎫－12，32 C.⎝⎛⎭⎫－32，12 D.⎝⎛⎭⎫12，－32解析：选B 设P (x ，y )，∵角α＝2π3在第二象限， ∴x ＝cos2π3＝－12，y ＝sin 2π3＝32，∴P ⎝⎛⎭⎫－12，32.2．如果角α的终边过点P (2sin 30°，－2cos 30°)，则sin α的值等于( ) A.12B ．－12C ．－32D ．－33解析：选C 由题意得P (1，－3)，它与原点的距离r ＝12＋(－3)2＝2，所以sin α＝－32. 3．若三角形的两内角α，β满足sin αcos β<0，则此三角形必为( ) A ．锐角三角形 B ．钝角三角形 C ．直角三角形D ．以上三种情况都可能解析：选B ∵sin αcos β<0，α，β∈(0，π)， ∴sin α>0，cos β<0，∴β为钝角． 4．代数式sin 120°cos 210°的值为( ) A ．－34B.34C ．－32D.14解析：选A 利用三角函数定义易得sin 120°＝32， cos 210°＝－32，∴sin 120°cos 210°＝32×⎝⎛⎭⎫－32＝－34，故选A.5．若角α的终边在直线y ＝－2x 上，则sin α等于( ) A ．±15B ．±55C ．±255D ．±12解析：选C 在α的终边上任取一点(－1,2)，则r ＝1＋4＝5，所以sin α＝y r ＝25＝255.或者取P (1，－2)，则r ＝1＋4＝5，所以sin α＝y r ＝－25＝－255.6．计算：tan π6＝________，csc π6＝________.解析：∵α＝π6，在α的终边上取一点P (3a ，a )，∴r ＝2a .∴tan π6＝33，csc π6＝2.答案：332 7．已知角α的终边过点P (5，a )，且tan α＝－125，则sin α＋cos α＝________. 解析：∵tan α＝a 5＝－125，∴a ＝－12.∴r ＝25＋a 2＝13. ∴sin α＝－1213，cos α＝513. ∴sin α＋cos α＝－713.答案：－7138．已知角θ的顶点与坐标原点重合，始边与x 轴的非负半轴重合，终边与射线y ＝3x (x ≥0)重合，则cos θ＝________.解析：根据题意，在射线上取一点P (1,3)，则x ＝1，y ＝3，r ＝12＋32＝10，所以cosθ＝x r ＝1010.答案：10109．已知角θ终边上有一点P (－3，m )，且sin θ＝24m (m ≠0)，试求cos θ与tan θ的值．解：点P (－3，m )到坐标原点O 的距离r ＝3＋m 2，由三角函数的定义，得sin θ＝yr＝m3＋m 2＝24m ，解得m ＝±5.∴r ＝2 2. 当m ＝5时，cos θ＝x r ＝－322＝－64，tan θ＝yx ＝5－3＝－153.当m ＝－5时，cos θ＝x r ＝－322＝－64，tan θ＝y x ＝－5－3＝153.10．已知点M 是圆x 2＋y 2＝1上的点，以射线OM 为终边的角α的正弦值为－22，求cos α和tan α的值．解：设点M 的坐标为(x 1，y 1)． 由题意，可知sin α＝－22，即y 1＝－22. ∵点M 在圆x 2＋y 2＝1上，∴x 21＋y 21＝1，即x 21＋⎝⎛⎭⎫－222＝1，解得x 1＝22或x 2＝－22.∴cos α＝22或cos α＝－22， ∴tan α＝－1或tan α＝1.层级二 应试能力达标1．已知角α的终边经过点(3a －9，a ＋2)，且cos α≤0，sin α>0，则实数a 的取值范围是( )A ．(－2,3]B ．(－2,3)C ．[－2,3)D ．[－2,3]解析：选A 由cos α≤0，sin α>0可知，角α的终边落在第二象限内或y 轴的正半轴上，所以有⎩⎪⎨⎪⎧3a －9≤0，a ＋2>0，即－2<a ≤3.2．设a <0，角α的终边与圆x 2＋y 2＝1的交点为P (－3a,4a )，那么sin α＋2cos α的值等于( )A.25B ．－25 C.15 D ．－15解析：选A ∵点P 在圆x 2＋y 2＝1上，则|OP |＝1. 即(－3a )2＋(4a )2＝1，解得a ＝±15. ∵a <0，∴a ＝－15. ∴P 点的坐标为⎝⎛⎭⎫35，－45. ∴sin α＝－45，cos α＝35. ∴sin α＋2cos α＝－45＋2×35＝25. 3．若tan x <0，且sin x －cos x <0，则角x 的终边在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析：选D ∵tan x <0，∴角x 的终边在第二、四象限，又sin x －cos x <0，∴角x 的终边在第四象限．4．已知角α的终边经过点P (m ，－6)，且cos α＝－45，则m ＝( ) A ．8B ．－8C ．4D ．－4 解析：选B 由题意r ＝|OP |＝m 2＋(－6)2＝m 2＋36，故cos α＝m m 2＋36＝－45，解得m ＝－8.5．已知角θ的顶点为坐标原点，始边为x 轴的正半轴，若P (4，y )是角θ终边上一点，且sin θ＝－255，则y ＝________. 解析：|OP |＝42＋y 2.根据任意角三角函数的定义得，y 42＋y 2＝－ 255，解得y ＝±8.又∵sin θ＝－255＜0及P (4，y )是角θ终边上一点，可知θ为第四象限角，∴y ＝－8. 答案：－86．设0≤θ＜2π，若sin θ＜0且cos 2θ＜0，则θ的取值范围是________．解析：因为0≤θ＜2π且sin θ＜0，所以π＜θ＜2π.又cos 2θ＜0，所以2k π＋π2＜2θ＜2k π＋3π2，k ∈Z ，所以k π＋π4＜θ＜k π＋3π4，k ∈Z.因为π＜θ＜2π，所以k ＝1，即θ的取值范围是5π4＜θ＜7π4. 答案：⎝⎛⎭⎫5π4，7π47．求下列函数的定义域：(1)f (x )＝ 2＋log 12x ＋tan x ；(2)f (x )＝cos x .解：(1)由题意得⎩⎨⎧ 2＋log 12x ≥0，x ≠k π＋π2(k ∈Z )， 即⎩⎪⎨⎪⎧ 0<x ≤4，x ≠k π＋π2(k ∈Z ). 解得0<x <π2或π2<x ≤4，所以原函数的定义域为⎝⎛⎭⎫0，π2∪⎝⎛⎦⎤π2，4. (2)若使函数有意义，则需满足cos x ≥0，即2k π－π2≤x ≤2k π＋π2，k ∈Z. ∴函数的定义域为⎣⎡⎦⎤2k π－π2，2k π＋π2，k ∈Z.8．已知1|sin α|＝－1sin α，且lg(cos α)有意义． (1)试判断角α所在的象限．(2)若角α的终边上一点是M ⎝⎛⎭⎫35，m ，且|OM |＝1(O 为坐标原点)，求m 的值及sin α的值．解：(1)由1|sin α|＝－1sin α，所以sin α<0，由lg(cos α)有意义，可知cos α>0， 所以α是第四象限角．(2)因为|OM |＝1，所以⎝⎛⎭⎫352＋m 2＝1，得m ＝±45. 又α为第四象限角，故m <0，从而m ＝－45， sin α＝y r ＝m |OM |＝－451＝－45.。

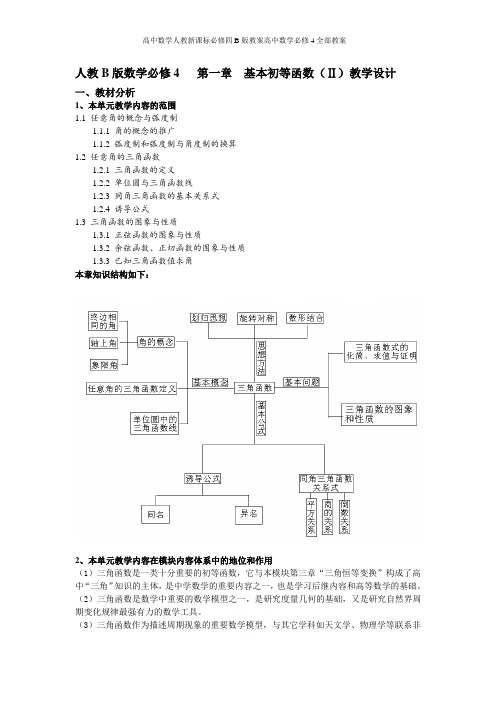
人教B版数学必修4 第一章基本初等函数（Ⅱ）教学设计一、教材分析1、本单元教学内容的范围1.1 任意角的概念与弧度制1.1.1 角的概念的推广1.1.2 弧度制和弧度制与角度制的换算1.2 任意角的三角函数1.2.1 三角函数的定义1.2.2 单位圆与三角函数线1.2.3 同角三角函数的基本关系式1.2.4 诱导公式1.3 三角函数的图象与性质1.3.1 正弦函数的图象与性质1.3.2 余弦函数、正切函数的图象与性质1.3.3 已知三角函数值求角本章知识结构如下：2、本单元教学内容在模块内容体系中的地位和作用（1）三角函数是一类十分重要的初等函数，它与本模块第三章“三角恒等变换”构成了高中“三角”知识的主体，是中学数学的重要内容之一，也是学习后继内容和高等数学的基础。

（2）三角函数是数学中重要的数学模型之一，是研究度量几何的基础，又是研究自然界周期变化规律最强有力的数学工具。

（3）三角函数作为描述周期现象的重要数学模型，与其它学科如天文学、物理学等联系非常紧密。

因此三角函数的学习可以培养学生的数学应用能力。

（4）三角函数的基础知识，主要是平面几何中的相似形和圆。

研究三角函数的方法，主要是在必修1中建立的研究初等函数的方法。

因此，通过对三角函数的学习，可以初步地把“数”与“形”联系起来。

（5）通过对三角函数的学习，不仅能使学生获得新的知识和技能，而且可以培养学生的辨证唯物主义观点，提高分析问题和解决问题的能力。

3、本单元教学内容总体教学目标 （1）任意角的概念、弧度制了解任意角的概念．了解弧度制的概念，能进行弧度与角度的互化． （2）任意角的三角函数理解任意角的正弦、余弦、正切的定义；了解任意角的余切、正割、余割的定义；并会利用单位圆中的有向线段表示正弦、余弦和正切，并理解其原理。

理解同角三角函数的基本关系式： 22sin cos 1x x +=，sin tan cos xx x=；借助单位圆的直观性探索正弦、余弦、正切的诱导公式，能进行同角三角函数之间的变换，会求任意角的三角函数值，并记住某些特殊角的三角函数值。

课题：§1.2任意角的三角函数（二）作业 总第____课时班级_______________姓名_______________一、填空题：1．如果角α的顶点在原点，始边与x 轴的正半轴重合，终边在函数5y x =- (0)x <的 图象上，那么cos α的值为 .2．若点P 在3π的终边上，且2OP =，则点P 的坐标 ． 3．角α的终边终过点(3,5)P a a -，那么2sin 3cos αα-的值是 ． 4．已知点(cos ,tan )p θθ在第三象限 ,则在区间[0,2)π内θ的取值范围是 . 5. 已知角α的终边上一点P 与点(3,2)A -关于y 轴对称，角β的终边上一点Q 与点A 关 于原点对称，则2sin 3sin αβ+的值为 ．6．角α（0<α<2π）的正、余弦线的长度相等，且正、余弦符号相异．则α的值为 . 7．若π4 <α < π2，则 sinα、cosα、tanα的大小关系为 < <________.8．若－2π３ ≤θ≤π6 ，利用三角函数线，可得sin θ的取值范围是 ．9．在(0,2)π内使sin cos x x >成立的x 的取值范围是 ．10．若0 < α < 2π，且sinα<23，cosα> 12 .利用三角函数线，得到α的取值范围是 .二、解答题：11．试作出角（1）πα43-=，（2）314π的正弦线、余弦线、正切线．12. 若α为锐角（单位为弧度），试利用单位圆及三角函数线，比较α，sin α,tan α之间 的大小关系。

13、利用三角函数线，写出满足下列条件的角x 的集合．⑴ sin x ≥22； ⑵ cos x ≤ 12 ； ⑶ tan x ≥－1 ；三、作业错误分析及订正：1．填空题错误分析：[错误类型分四类：①审题错误；②计算错误；③规范错误；④知识_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ 3．解答题订正：。

教学设计人教B版2021版。

必修4 1.2.1三角函数的定义（第一课时）一、【教学目标】1、知识与技能目标：（1）理解任意角的正弦、余弦、正切的定义；了解任意角的余切、正割、余割的定义。

（2）会利用三角函数的定义分析、解决一些三角函数求值、确定三角函数的符号问题。

2、过程与方法目标：由三角函数的定义引导学生自主研究同角三角函数的基本关系式，提高学生的建模意识。

培养学生发现问题、分析问题、解决问题的能力，特殊到一般的思维方法，渗透分类讨论思想及转化思想，优化思维品质．3、情感与态度目标：通过经历的用三角函数的定义出发，求三角函数值，激发学生的求知欲，鼓励学生积极参与、大胆尝试、勇于探索、敢于创新，磨练思维品质，从中获得成功的体验。

引导学生养成自主学习的学习习惯。

二、【学情分析】1学生具备初中三角函数的定义，高中终边相同的角的概念方面的知识。

2、这个班级是营口市第二高级中学的理科普通班，学生基础知识掌握一般。

有学习积极性。

有一定的参与意识。

三、【教学重点、难点】（一）教学重点三角函数的定义，明确对应法则和定义域。

（二）教学难点1 通过坐标求任意角的三角函数的值，判断三角函数在各个象限的符号。

2、对学生进行思维灵活性的培养。

在解题过程中常常要分类讨论思想，提高学生从特殊到一般的概括能力。

四、【教学方法】讲练结合【教学过程】1.2.1三角函数的定义（第一课时）1.2.1教学活动【预习要求】1掌握任意角的正弦、余弦、正切的定义；2掌握正弦、余弦、正切函数的定义域。

【预习】教材第14-16页，1初中知识再现：在初中我们学习了锐角三角函数，它是以锐角为自变量，边的比值为函数值的三角函数:sin α= ；cos α=tan α=cot α=2．任意角的三角函数：设是一个任意角，在的终边上任取（异于原点的）一点P,， 则P 与原点的距离02222>+=+=y x y x r 根据三角形的相似知识得到xyr y r x ,,均为定值。

任意角的三角函数__________________________________________________________________________________ __________________________________________________________________________________ 1.能根据三角函数的定义导出同角三角函数的基本关系式及它们之间的联系； 2.熟练掌握已知一个角的三角函数值求其它三角函数值的方法。

3.牢固掌握同角三角函数的两个关系式，并能灵活运用于解题. （一）任意角的三角函数： 任意点到原点的距离公式：22y x r +=1.三角函数定义：在直角坐标系中，设α是一个任意角，α终边上任意一点P （除了原点）的坐标为(,)x y ，它与原点的距离为(0)r r ==>，那么（1）比值y r 叫做α的正弦，记作sin α，即sin y r α=； （2）比值x r 叫做α的余弦，记作cos α，即cos xr α=；（3）比值y x 叫做α的正切，记作tan α，即tan yxα=；（4）比值x y 叫做α的余切，记作cot α，即cot x yα=； 2.说明：（1）α的始边与x 轴的非负半轴重合，α的终边没有表明α一定是正角或负角，以及α的大小，只表明与α的终边相同的角所在的位置；（2）根据相似三角形的知识，对于确定的角α，四个比值不以点(,)P x y 在α的终边上的位置的改变而改变大小； （3）当()2k k Z παπ=+∈时，α的终边在y 轴上，终边上任意一点的横坐标x 都等于0，所以tan yxα=无意义；同理当()k k Z απ=∈时，y x =αcot 无意义；（4）除以上两种情况外，对于确定的值α，比值y r 、x r 、yx、x y 分别是一个确定的实数。

正弦、余弦、正切、余切是以角为自变量，比值为函数值的函数，以上四种函数统称为三角函数。

三角函数的定义一、教学目标1.知识与技能目标（1）理解并掌握任意角三角函数的定义，了解终边相同的角的同一三角函数值相等；（2）掌握三角函数（正弦、余弦、正切）的定义域；（3）熟记三角函数在各象限的符号.2.过程与方法目标（1）培养学生应用图形分析数学问题的能力；（2）通过对任意角三角函数的定义的探究，培养学生自主探究、合作交流的能力；3.情感、态度与价值观目标通过三角函数定义的学习，体会同一角的三角函数值，不因在其终边上取点的变化而变化，从而启示我们在研究问题时，要在千变万化中，抓住事物的本质属性，不被表面现象所迷惑，从中体会三角函数，像一般实函数一样，体现了一般函数的抽象美。

二、教学重难点重点：任意角的三角函数的定义，三角函数的定义域，判定三角函数值的符号.难点：任意角的三角函数的定义.三、教学方法在教学中以问题为核心，采取“导引体验式”教学方法．在复习锐角三角函数定义的基础上，引导学生重新定义任意角的三角函数，由边的比变为坐标与距离、坐标与坐标、距离与坐标的比，使学生在理解掌握定义的基础上，加深特殊与一般关系的理解．然后引导学生根据三角函数定义和象限内的点坐标符号导出三角函数在各象限的符号．【教学过程】新课例题讲解、变式训练探究：三角函数在各象限的符号．三角函数在各象限的符号如下图所示：例题2. 确定下列各三角函数值的符号：（1）cos260°例题3.设sinα<0且tanα>0, 试确定α是第几象限角？变式训练2.10tan3π（1）（）的符号sin cos0,ααα⋅<（2）则是第几象限角？(3)cos22βββ、已知是第三象限角且<0，问是第几象限角？学生探究得到三角函数在各象限的符号，教师可以引导学生总结口诀，帮助学生记忆：Ⅰ全正，Ⅱ正弦，Ⅲ正切，Ⅳ余弦．教师：PPT展示求解过程并点明，解决这一类问题主要就是判断角的终边落在哪一个象限，并且熟记三角函数在各个象限的符号.教师也可以借助超级画板动态演示，可以更直观形象的得到三角函数在各象限的符号，符合新课程理念提出的借助信息技术辅助教学，同时也是直观教学的一种体现..例题的讲解主要是让学生体会如何利用三角函数在各象限的符号解决问题，加深学生对这一部分知识的体会.小结本节课所学知识点：内容总结：(1)任意角三角函数的定义．(2三角函数的定义域．(3)任意角三角函数值的符号（记住口诀）．思想方法方面：（1）定义法求解三角函数值.让学生总结，教师适当的提醒给予补充完整．培养学生的语言组织总结能力和数学语言表达能力．O xy＋＋－－sin αO xy＋－＋－cos αO xy＋－－＋tan αsin-3π（2）（）。

人大附中分校高一数学导学学案1．单位圆的概念. 2．有向线段的概念. 3．用正弦线、余弦线、正切线表示任意角的三角函数值.．分别作出和例2．利用单位圆和三角函数线比较大小：(1> sin1和sin1.5。

(2> cos1和cos1.5。

(3> tan2和tan3.(1> sin1<sin1.5。

(2> cos1>cos1.5。

(3> tan2<tan3.例3. 已知sinx=0.5，利用单位圆和三角函数线求角x的大小.(0º<x<360º> 30°和150°随堂练习1．对三角函数线，下列说法正确的是( >A．对任何角都能作出正弦线、余弦线和正切线B．有的角正弦线、余弦线和正切线都不存在C．任何角的正弦线、正切线总是存在，但余弦线不一定存在D．任何角的正弦线、余弦线总是存在，但是正切线不一定存在解读：选 D.正弦函数和余弦函数的定义域是R，所以任何角的正弦线、余弦线总是存在，正切函数的定义域不是R，所以任何角的正切线不一定存在．b5E2RGbCAP2．角α(0<α<2π>的正弦线与余弦线长度相等且符号相同，那么α的值为( >A.错误!或错误!πB.错误!或错误!πC.错误!或错误!πD.错误!或错误!πp1EanqFDPw解读：选C.由条件知sinα＝cosα，又0<α<2π，∴α＝错误!或错误!.3．若角α的正切线位于第一象限，则角α属于( >A．第一象限 B．第一、二象限C．第三象限 D．第一、三象限解读：选 D.由正切线的定义知，当角α是第一、三象限的角时，正切线都在第一象限．4．不等式cosα≤错误!的解集为____________________________．DXDiTa9E3d解读：画出单位圆，然后画出直线x＝错误!，从图形中可以看出．答案：{α|2kπ＋错误!≤α≤2kπ＋错误!，k∈Z}申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

1。

2.2单位圆与三角函数线学习目标1。

了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切。

2.能利用三角函数线解决一些简单的三角函数问题。

知识点一单位圆思考1什么叫单位圆？思考2点的射影是如何定义的?梳理(1)单位圆把________的圆叫做单位圆.(2)单位圆中角α的坐标角α的余弦和正弦分别等于角α终边与单位圆交点的________和________.知识点二三角函数线思考1三角函数线的长度等于三角函数的值吗?思考2三角函数线的方向与三角函数值的正负有什么联系？梳理三角函数线类型一三角函数线例1作出－错误!的正弦线、余弦线和正切线.反思与感悟（1）作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得到正弦线和余弦线.（2)作正切线时，应从点A（1，0）引单位圆的切线交角的终边或终边的反向延长线于一点T,即可得到正切线AT.跟踪训练1在单位圆中画出满足sin α＝错误!的角α的终边,并求角α的取值集合。

类型二利用三角函数线比较大小例2利用三角函数线比较sin错误!和sin错误!,cos错误!和cos错误!，tan错误!和tan错误!的大小。

反思与感悟利用三角函数线比较三角函数值的大小时，一般分三步：（1)角的位置要“对号入座”。

(2)比较三角函数线的长度.(3）确定有向线段的正负。

跟踪训练2比较sin 1 155°与sin(－1 654°)的大小.类型三利用三角函数线解不等式（组)命题角度1利用三角函数线解不等式组例3在单位圆中画出适合下列条件的角α的终边的范围，并由此写出角α的集合。

（1)sin α≥错误!；(2)cos α≤－错误!.反思与感悟用单位圆中的三角函数线求解简单的三角不等式，应注意以下两点：(1）先找到“正值"区间，即0~2π内满足条件的角θ的范围，然后再加上周期。

(2)注意区间是开区间还是闭区间。

第一章 三角函数1.2.1 任意角的三角函数一、选择题1．已知sin α+cos α=–15，α∈（0，π），则tan α的值为A ．–43或–34B ．–43C ．–34D ．34【答案】C【解析】∵sin α+cos α=–15，α∈（0，π），∴α为钝角，结合sin 2α+cos 2α=1，∴sin α=35，cos α=–45，则tan α=sin cos αα=–34，故选C ． 2．若点5π5πsin cos 66⎛⎫ ⎪⎝⎭，在角α的终边上，则sin α的值为A ．12-B ．12C ．3D 3 【答案】C【解析】因为点5π5πsin cos 66⎛⎫ ⎪⎝⎭，在角α的终边上，即点132⎛- ⎝⎭，在角α的终边上，则3sin α=，故选C ．3．若角α的终边过点P （3，–4），则cos α等于A ．35B ．34-C ．45-D ．45【答案】A【解析】∵角α的终边过点P （3，–4），∴r =5，∴cos α=35，故选A ．4．如果角θ的终边经过点（3，–4），那么sin θ的值是A ．35B ．35-C ．45D ．45-【答案】D【解析】∵角θ的终边经过点（3，–4），∴x =3，y =–4，r 22x y +，∴sin θ=y r=–45，故选D ．5．若sinαtanα<0，且costanαα<0，则角α是A．第一象限B．第二象限C．第三象限D．第四象限【答案】C【解析】∵sinαtanα<0，可知α是第二或第三象限角，又costanαα<0，可知α是第三或第四象限角．∴角α是第三象限角．故选C．6．已知点P（x，3）是角θ终边上一点，且cosθ=–45，则x的值为A．5 B．–5 C．4 D．–4 【答案】D【解析】∵P（x，3）是角θ终边上一点，且cosθ=–45，∴cosθ=29x+=–45，∴x=–4．故选D．7．若点P（sinα，tanα）在第三象限，则角α是A．第一象限角B．第二象限角C．第三象限角D．第四象限角【答案】D【解析】∵点P（sinα，tanα）在第三象限，∴sinα<0，tanα<0．∴角α是第四象限角．故选D．8．如果角α的终边过点（2sin60°，–2cos60°），则sinα的值等于A．12B．–12C．–3D．–3【答案】B【解析】角α的终边过点（2sin60°，–2cos60°），即（31-，），由任意角的三角函数的定义可知：sinα=()()221 231=-+-．故选B．9．若角120°的终边上有一点（–4，a），则a的值是A．43B．43-C．43±D．310．已知4sin5α=，并且P（–1，m）是α终边上一点，那么tanα的值等于A ．43-B ．34-C ．34D ．43【答案】A 【解析】∵4sin5α=，并且P （–1，m ）是α45=，∴m =43，那么tan α=1m-= –m =–43，故选A ． 11．已知sin α<0，且tan α>0，则α的终边所在的象限是A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】∵sin α<0，∴α的终边在第三、第四象限或在y 轴负半轴上，∵tan α>0，∴α的终边在第一或第三象限，取交集可得，α的终边所在的象限是第三象限角．故选C ． 12．若角α终边经过点P （sin2π2πcos 33，），则sin α=A ．12BC ．12-D ． 【答案】C【解析】∵角α终边经过点P （sin 2π2πcos 33，），即点P ，–12），∴x ，y =–12，r =|OP |=1，则sin α=y r=y =–12，故选C ．13．已知角α的终边过点12P ⎛ ⎝⎭，，则sin α=A ．12B C D ． 【答案】C【解析】由题意可得，x =12，y ，r =|OP |=1，∴sin α=y r，故选C ．14．已知角α的终点经过点（–3，4），则–cos α=A ．35B ．–35C ．45D ．–45【答案】A【解析】∵角α的终点经过点（–3，4），∴x =–3，y =4，r =|OP |=5，则–cos α=–35x r =，故选A ． 二、填空题15．若角α的终边与单位圆交于P （–35，45），则sin α=45；cos α=___________；tan α=___________．【答案】45；35-；43- 【解析】∵角α的终边与单位圆交于P （–35，45），|OP |=223455⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭=1，∴由任意角的三角函数的定义可知：sin α=44515=，同理可得cos α=35-；tan α=445335=--；故答案为：45；35-；43-．16．已知23cos 4a x a-=-，x 是第二、三象限角，则a 的取值范围是__________．17．已知角α的终边经过点P （–2，4），则sin α–cos α的值等于__________．35【解析】∵角α的终边经过点P （–2，4），∴x =–2，y =4，r =|OP 5，∴sin α=25y r =，cos α=xr= 5，则sin α–cos α3535． 18．适合条件|sin α|=–sin α的角α是__________．【答案】[2k π–π，2k π]，k ∈Z【解析】∵|sin α|=–sin α，∴–sin α≥0，∴sin α≤0，由正弦曲线可以得到α∈[2k π–π，2k π]，k ∈Z ，故答案为：[2k π–π，2k π]，k ∈Z ．19．若角α的终边经过点（–1，–2），则tan α=___________．【答案】2【解析】∵角α的终边经过点（–1，–2），∴由三角函数定义得tan α=21--=2．故答案为：2． 20．已知角θ的终边经过点P （x ，2），且1cos 3θ=，则x =___________．2 【解析】∵角θ的终边经过点P （x ，2），且21cos 34x θ==+，解得x 22．21．若sinθ<0，cosθ>0，则θ在第___________象限．【答案】四【解析】由sinθ<0，可知θ为第三、第四象限角或终边在y轴负半轴上的角．由cosθ<0，可知θ为第一、第四象限角或终边在x轴正半轴上的角．取交集可得，θ在第四象限．故答案为：四．三、解答题22．已知点P（3m，–2m）（m<0）在角α的终边上，求sinα，cosα，tanα．【解析】因为点P（3m，–2m）（m<0）在角α的终边上，所以x=3m，y=–2m，r=–13m，sinα=21313yr==，cosα=31313xr=-=-，tanα=32yx=-．23．确定下列各式的符号：（1）sin 103°·cos 220°；（2）cos 6°·tan 6.24．已知角α的终边在直线y=2x上，分别求出sinα，cosα及tanα的值．【解析】当角α的终边在第一象限时，在角α的终边上任意取一点P（1，2），则x=1，y=2，r=|OP5，∴sinα=255yr==cosα=55xr=，tanα=yx=2；当角α的终边在第三象限时，在角α的终边上任意取一点P（–1，–2），则x=–1，y=–2，r=|OP|=5，∴sinα=yr=5=25，cosα=xr=5=5，tanα=yx=2．25．已知角α的终边上一点P （m ）（m ≠0），且sin α=4，求cos α，tan α的值．【解析】设P （x ，y ）．由题设知x=y=m ，所以r 2=|OP|2=（2+m 2（O 为原点），，所以sin α=mr =4，所以=，3+m 2=8，解得当r=，x=所以cos =，tan当m=r=，x=y=所以cos =，tan26．已知角α终边上一点P （m ，1），cos α=–13．（1）求实数m 的值； （2）求tan α的值．【解析】（1）角α终边上一点P （m ，1），∴x =m ，y =1，r =|OP∴cos α=–13，解得m =．（2）由（1）可知tan α=1m。