最新2019中考数学专题复习过关集训 第四单元 三角形 第4课时 全等三角形练习习题 新人教版
- 格式:doc
- 大小:171.50 KB
- 文档页数:13
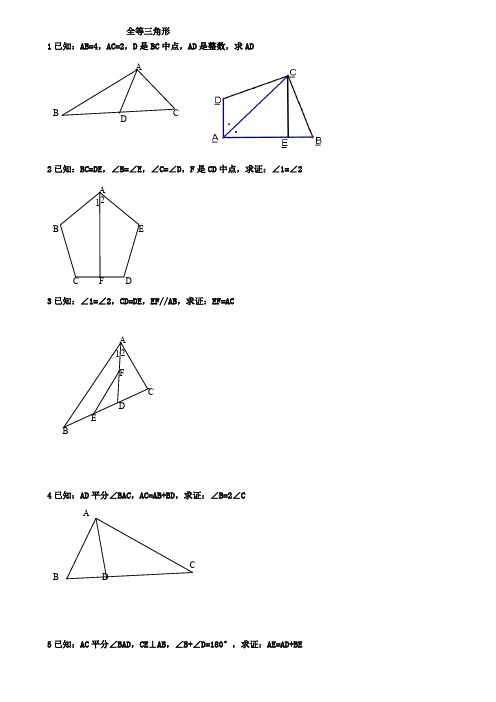
全等三角形1已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC4已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C5已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE CDBADB CAB ACDF2 1E6 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
7已知:AB=CD ,∠A=∠D ,求证:∠B=∠C8.P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB9已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DCP DAC B10.如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD+BC=AB .11如图,△ABC 中,AD 是∠CAB 的平分线,且AB=AC+CD ,求证:∠C=2∠B12如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
13已知:如图,AB=AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F 。
求证:BE=CD . PEDCBA D CBAMFECBACD F14在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.15如图所示,已知AE ⊥AB ,AF ⊥AC ,AE=AB ,AF=AC 。


第四节全等三角形姓名:________ 班级:________ 限时:______分钟1.(2018·安徽)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AEC.BD=CE D.BE=CD2.(2018·黔南州)下列各图中a,b,c为三角形的边长,则甲,乙,丙三个三角形和左侧△ABC全等的是( )A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙3.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )A. 75°B. 70°C. 65°D. 60°4.(2018·南京)如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )A.a+c B.b+c C.a-b+c D.a+b-c5.(2018·临沂)如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE 的长是( )A.32B .2C .2 2D.106.(2018·济宁)在△ABC 中,点E ,F 分别是边AB ,AC 的中点,点D 在BC 边上,连接DE ,DF ,EF ,请你添加一个条件________,使△BED 与△FDE 全等.7.(2018·金华)如图,△ABC 的两条高AD ,BE 相交于点F ,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是________.8.(2018·福州质检)如图,点B ,F ,C ,E 在一条直线上,AB∥DE,AC∥DF 且AC =DF ,求证:AB =DE.9.(2018·云南省卷)如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.10.(2018·泰州)如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.11.(2018·陕西)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H.若AB=CD,求证:AG=DH.12.(2017·恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P. 求证:∠AOB=60°.13.(2018·恩施州)如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O. 求证:AD与BE互相平分.14.(2018·怀化)已知:如图,点A,F,E,C在同一直线上,AB∥DC,AB=CD,∠B=∠D.(1)求证:△ABE≌△CDF;(2)若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.1.(2018·桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.(1)求证:△ABC≌△DEF;(2)若∠A=55°,∠B=88°,求∠F的度数.2.(2018·衡阳)如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.(1)求证:△ABE≌△DCE;(2)当AB=5时,求CD的长.3.(2018·莆田质检)如图,在△ABC中,AB=BC,∠ABC=90°,分别以AB,AC为边在AB同侧作等边△ABD和等边△ACE,连接DE.(1)判断△ADE的形状,并加以证明;(2)过图中两点画一条直线,使其垂直平分图中的某条线段,并说明理由.4.(2018·哈尔滨)已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点G,∠BGE=∠ADE.(1)如图①,求证:AD=CD;(2)如图②,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图②中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.5.(2018·滨州)已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.参考答案【基础训练】1.D 2.B 3.C 4.D 5.B 6.D 是BC 的中点7.AC =BC8.证明: ∵AB∥DE,AC∥DF,∴∠B=∠E,∠ACB=∠DFE.在△ABC 和△DEF 中,⎩⎪⎨⎪⎧∠B=∠E ∠ACB=∠DFE,AC =DF∴△ABC≌△DEF(AA S ),∴AB=DE.9.证明:∵AC 平分∠BAD,∴∠BAC=∠DAC,在△ABC 和△ADC 中,⎩⎪⎨⎪⎧AB =AD ∠BAC=∠DAC,AC =AC∴△ABC≌△ADC.10.证明:在Rt △ABC 和Rt △DCB 中,⎩⎪⎨⎪⎧AC =BD ,CB =BC , ∴Rt △ABC≌Rt △DCB(HL ),∴∠OBC=∠OCB,∴BO=CO.11.证明: ∵AB∥CD.∴∠A=∠D.∵EC∥BF.∴∠BHA=∠CGD.∵AB=CD ,∴△ABH≌△DCG.∴AH=DG.∴AG=DH.12.证明:∵△ABC、△CDE 为等边三角形,∴∠ACB=∠ECD=60°,AC =BC ,CD =CE ,∴∠ACE=∠BCD,在△ACE 和△BCD 中,⎩⎪⎨⎪⎧AC =BC ,∠ACE=∠BCD,CE =CD ,∴△ACE≌△BCD(S A S ),∴∠CAE=∠CBD,∵∠AOB+∠CBD+∠BPO=180°,∠BCA +∠CAE+∠APC=180°,且∠BPO=∠APC,∴∠AOB=∠BCA=60°.13.证明:如解图,连接BD ,AE ,∵FB=CE ,∴BC=EF ,又∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB=∠DFE,在△ABC 和△DEF 中,⎩⎪⎨⎪⎧∠ABC=∠DEF,BC =EF ,∠ACB=∠DFE,∴△ABC≌△DEF(A S A),∴AB=DE ,又∵AB∥DE,∴四边形ABDE 是平行四边形,∴AD 与BE 互相平分.14.证明:(1)∵AB∥DC,∴∠A=∠C.在△ABE 和△CDF 中,⎩⎪⎨⎪⎧∠A=∠C,AB =CD ,∠B=∠D,∴△ABE≌△CDF(A S A);(2)解:∵点E ,G 分别为线段FC ,FD 的中点,∴EG=12CD ,∵EG=5,∴CD=10,∵△ABE≌△CDF,∴AB=CD =10.【拔高训练】1.(1)证明:∵AC=AD +DC ,DF =DC +CF ,且AD =CF ,∴AC=DF ,在△ABC 和△DEF 中,⎩⎪⎨⎪⎧AB =DE BC =EF ,AC =DF∴△ABC≌△DEF(SSS );(2)解:由(1)可知,∠F=∠ACB.∵∠A=55°,∠B=88°,∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°,∴∠F=∠ACB=37°.2.(1)证明:在△AEB 和△DEC 中,⎩⎪⎨⎪⎧AE =DE ∠AEB=∠DEC,BE =EC∴△AEB≌△DEC(S A S ).(2)解:∵△AEB≌△DEC,∴AB=CD ,∵AB=5,∴CD=5.3.解: (1)△ADE 是等腰直角三角形.理由:在等边△ABD 和等边△ACE 中,∵BA=DA ,CA =EA ,∠BAD=∠CAE=60°,∴∠BAD-∠CAD=∠CAE-∠CAD.即∠BAC=∠EAD,∴△ABC≌△ADE.∴BC=DE ,∠ABC=∠ADE,∵AB=BC =AD ,∠ABC=90°,∴AD=DE ,∠ADE=90°,即△ADE 是等腰直角三角形.(2)连接CD ,则直线CD 垂直平分线段AE.(或连接BE ,则直线BE 垂直平分线段AC) 理由:由(1)得DA =DE.又∵CA=CE ,∴直线CD 垂直平分线段AE.4.(1)证明:∵∠BGE=∠ADE,∠BGE=∠CGF,∴∠ADE=∠CGF,∵AC⊥BD,BF⊥CD,∴∠ADE+∠DAE=∠CGF+∠GCF,∴∠DAE=∠GCF,∴AD=CD.(2)解:△ACD、△ABE、△BCE、△BHG.【解法提示】设DE =a ,则AE =2DE =2a ,EG =DE =a ,∵S △ADE =12AE·DE=12·2a·a=a 2, ∵BH 是△ABE 的中线,∴AH=HE =a ,∵AD=CD ,AC⊥BD,∴CE=AE =2a ,则S △ADC =12AC·DE=12·(2a+2a)·a=2a 2=2S △ADE ; 在△ADE 和△BGE 中,⎩⎪⎨⎪⎧∠AED=∠BEG DE =GE ,∠ADE=∠BGE∴△ADE≌△BGE(A S A),∴BE=AE =2a ,∴S △ABE =12AE·BE=12·2a·2a=2a 2, S △BCE =12CE·BE=12·2a·2a=2a 2, S △BHG =12HG·BE=12·(a +a)·2a=2a 2, 综上,面积等于△ADE 面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.5.(1)证明:连接AD ,如解图①所示.第5题解图①∵∠A=90°,AB =AC ,∴△ABC 为等腰直角三角形,∠EBD=45°.∵点D 为BC 的中点,∴AD=12BC =BD ,∠FAD=45°. ∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,∴∠BDE=∠ADF.在△BDE 和△ADF 中,⎩⎪⎨⎪⎧∠EBD=∠FAD BD =AD ,∠BDE=∠ADF∴△BDE≌△ADF(A S A),∴BE=AF.(2)解:BE =AF ,证明如下:连接AD ,如解图②所示.第5题解图②∵∠ABD=∠BAD=45°,∴∠EBD=∠FAD=135°.∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°, ∴∠EDB=∠FDA.在△EDB 和△FDA 中,⎩⎪⎨⎪⎧∠EBD=∠FAD BD =AD∠EDB=∠FDA, ∴△EDB≌△FDA(A S A),∴BE=AF.。
第四节 全等三角形姓名: ________ 班级: ________ 限时: ______分钟1.( 2018·安徽 ) 如图,点 D ,E 分别在线段 AB ,AC 上, CD 与 BE 订交于 O 点,已知 AB =AC ,现增添以下的哪个条件仍不可以判断△ ABE ≌△ ACD( )A .∠B =∠ CB .AD =AEC .BD =CED .BE =CD2.( 2018·黔南州 ) 以下各图中 a ,b ,c 为三角形的边长,则甲,乙,丙三个三 角形和左边△ ABC 全等的是 ()A .甲和乙B .乙和丙C .甲和丙D .只有丙3.如图,△ ABC 中, AB =AC ,BD =CE ,BE =CF ,若∠ A =50°,则∠ DEF 的度数是( )A. 75 °B. 70 °C. 65 ° 4. ( 2018· 南京 ) 如图, AB ⊥CD ,且D. 60 °AB =CD.E 、F是AD上两点,CE ⊥AD ,BF ⊥AD.若 CE =a ,BF =b ,EF =c ,则 AD 的长为 ( )A.a+c B .b+c C .a-b+c D .a+b-c5. ( 2018·临沂 ) 如图,∠ ACB=90°, AC=BC,AD⊥CE,BE⊥CE,垂足分别是点 D、E,AD=3,BE=1,则 DE的长是 ()3A. 2B.2C.2 2D. 106.( 2018·济宁 ) 在△ ABC中,点 E,F 分别是边 AB,AC的中点,点 D 在 BC边上,连结 DE,DF,EF,请你增添一个条件 ________,使△ BED与△ FDE全等.7.( 2018·金华 ) 如图,△ ABC的两条高 AD,BE订交于点 F,请增添一个条件,使得△ ADC≌△ BEC(不增添其余字母及协助线 ) ,你增添的条件是 ________.8.( 2018·福州质检 ) 如图,点 B,F,C,E 在一条直线上, AB∥DE,AC∥DF 且AC=DF,求证: AB=DE.9.( 2018·云南省卷 ) 如图,已知 AC均分∠ BAD, AB=AD.求证:△ ABC≌△ ADC.10.( 2018·泰州 ) 如图,∠ A=∠ D=90°, AC=DB,AC、DB订交于点 O.求证:OB=OC.11.( 2018·陕西 ) 如图, AB∥CD, E、F 分别为 AB、CD上的点,且EC∥BF,连接 AD,分别与 EC、BF 订交于点 G、H.若 AB=CD,求证: AG=DH.12.( 2017·恩施州 ) 如图,△ ABC、△ CDE均为等边三角形,连结BD、AE交于点O,BC与 AE交于点 P.求证:∠ AOB=60°.13.( 2018·恩施州 ) 如图,点 B、 F、C、E 在一条直线上, FB= CE,AB∥ED,AC∥FD, AD交 BE于 O.求证: AD与 BE相互均分.14.( 2018·怀化 ) 已知:如图,点A,F,E, C 在同向来线上, AB∥DC, AB=CD,∠ B=∠ D.(1)求证:△ ABE≌△ CDF;(2)若点 E,G分别为线段 FC,FD的中点,连结 EG,且 EG=5,求 AB的长.1.( 2018·桂林 ) 如图,点A、D、C、F 在同一条直线上, AD=CF,AB=DE,BC =E F.(1)求证:△ ABC≌△ DEF;(2)若∠ A=55°,∠ B=88°,求∠F的度数.2.( 2018·衡阳 ) 如图,已知线段AC,BD订交于点 E,AE=DE,BE=CE.(1)求证:△ ABE≌△ DCE;(2)当 AB=5 时,求 CD的长.3.( 2018·莆田质检 ) 如图,在△ ABC中, AB=BC,∠ ABC=90°,分别以AB,AC为边在 AB同侧作等边△ ABD和等边△ ACE,连结 DE.(1)判断△ ADE的形状,并加以证明;(2)过图中两点画一条直线,使其垂直均分图中的某条线段,并说明原因.4.( 2018·哈尔滨 ) 已知:在四边形 ABCD中,对角线 AC、BD 订交于点 E,且AC⊥BD,作 BF⊥CD,垂足为点 F,BF与 AC交于点 G,∠ BGE=∠ ADE.(1)如图①,求证: AD=CD;(2)如图②, BH是△ ABE的中线,若 AE=2DE,DE=EG,在不增添任何协助线的状况下,请直接写出图②中四个三角形,使写出的每个三角形的面积都等于△ADE面积的 2 倍.5.( 2018·滨州 ) 已知,在△ ABC中,∠ A=90°, AB=AC,点 D为 BC的中点.(1)如图①,若点 E、F 分别为 AB、AC上的点,且 DE⊥DF,求证: BE=AF;(2)若点 E、F 分别为 AB、CA延伸线上的点,且 DE⊥DF,那么 BE=AF吗?请利用图②说明原因.参照答案【基础训练】:1.D 2.B 3.C 4.D 5.B 6.D 是 BC的中点7.AC=BC8.证明:∵AB∥DE,AC∥DF,∴∠ B=∠ E,∠ ACB=∠ DFE.在△ ABC和△ DEF中,∠B=∠E∠ACB=∠ DFE,AC=DF∴△ ABC≌△ DEF(AA S) ,∴ AB=DE.9.证明:∵ AC均分∠ BAD,∴∠ BAC=∠ DAC,在△ ABC和△ ADC中,AB=AD∠BAC=∠ DAC,∴△ ABC≌△ ADC.AC=ACAC=BD,10.证明:在Rt△ABC和Rt△DCB中,CB=BC,∴R t△ABC≌ Rt△DCB(HL),∴∠ OBC=∠ OCB,∴BO=CO.11.证明:∵AB∥CD.∴∠ A=∠ D.∵EC∥BF.∴∠ BHA=∠ CGD.∵AB=CD,∴△ ABH≌△ DCG.∴AH=DG.∴AG= DH.12.证明:∵△ ABC、△ CDE为等边三角形,∴∠ ACB=∠ ECD=60°, AC=BC,CD=CE,∴∠ ACE=∠ BCD,在△ ACE和△ BCD中,AC=BC,∠ACE=∠ BCD,CE=CD,∴△ ACE≌△ BCD(S A S) ,∴∠ CAE=∠ CBD,∵∠ AOB+∠ CBD+∠ BPO=180°,∠BCA+∠ CAE+∠ APC=180°,且∠ BPO=∠ APC,∴∠ AOB=∠ BCA=60°.13.证明:如解图,连结 BD,AE,∵FB=CE,∴BC=EF,又∵ AB∥ED,AC∥FD,∴∠ ABC=∠ DEF,∠ ACB=∠ DFE,在△ ABC和△ DEF中,∠ABC=∠ DEF,BC=EF,∠ACB=∠ DFE,∴△ ABC≌△ DEF(A S A),∴ AB=DE,又∵ AB∥DE,∴四边形 ABDE是平行四边形,∴AD与 BE相互均分.14.证明: (1) ∵AB∥DC,∴∠ A=∠ C.在△ ABE和△ CDF中,∠A=∠ C,AB=CD,∴△ ABE≌△ CDF(A S A);∠B=∠ D,(2)解:∵点 E,G分别为线段 FC,FD的中点,1∴EG=2CD,∵EG=5,∴ CD=10,∵△ ABE≌△ CDF,∴AB=CD=10.【拔高训练】:1.(1) 证明:∵ AC=AD+DC,DF=DC+CF,且 AD=CF,∴AC=DF,在△ ABC和△ DEF中,AB=DEBC=EF,∴△ ABC≌△ DEF(SSS);AC=DF(2)解:由 (1) 可知,∠ F=∠ ACB.∵∠ A=55°,∠ B=88°,∴∠ ACB=180°- ( ∠A+∠ B)=180°- (55 °+ 88°) =37°,∴∠ F=∠ ACB=37°.AE=DE2.(1) 证明:在△ AEB和△ DEC中,∠AEB=∠ DEC,BE=EC∴△ AEB≌△ DEC(S A S) .(2)解:∵△ AEB≌△ DEC,∴ AB= CD,∵AB=5,∴ CD=5.3.解: (1) △ADE是等腰直角三角形.原因:在等边△ABD和等边△ACE中,∵BA=DA,CA=EA,∠ BAD=∠ CAE=60°,∴∠ BAD-∠ CAD=∠CAE-∠ CAD.即∠ BAC=∠ EAD,∴△ ABC≌△ ADE.∴BC=DE,∠ ABC=∠ ADE,∵AB=BC=AD,∠ ABC=90°,∴AD=DE,∠ ADE=90°,即△ ADE是等腰直角三角形.(2)连结 CD,则直线 CD垂直均分线段 AE.( 或连结 BE,则直线 BE垂直均分线段AC)原因:由 (1) 得 DA=DE.又∵ CA= CE,∴直线 CD垂直均分线段 AE.4.(1) 证明:∵∠ BGE=∠ ADE,∠ BGE=∠ CGF,∴∠ ADE=∠ CGF,∵AC⊥BD,BF⊥CD,∴∠ ADE+∠ DAE=∠ CGF+∠ GCF,∴∠ DAE=∠ GCF,∴ AD= CD.(2) 解:△ ACD、△ ABE、△ BCE、△ BHG.【解法提示】:设 DE=a,则AE=2DE=2a,EG=DE=a,112∵S△ADE=2AE·DE=2·2a·a=a,∵BH是△ ABE的中线,∴AH=HE=a,∵AD=CD,AC⊥BD,∴ CE= AE=2a,11则S△ADC=2AC·DE=2·(2a +2a) ·a= 2a2=2S△ADE;在△ ADE和△ BGE中,∠AED=∠ BEGDE=GE,∠ADE=∠ BGE∴△ ADE≌△ BGE(A S A),∴ BE=AE=2a,△ABE 112,∴S=2AE·BE=2·2a·2a=2a112S△BCE=2CE·BE=2·2a·2a=2a ,112S△BHG=2HG·BE=2·(a+a) ·2a= 2a,综上,面积等于△ ADE面积的 2倍的三角形有△ ACD、△ ABE、△ BCE、△ BHG. 5.(1) 证明:连结 AD,如解图①所示 .第 5 题解图①∵∠ A=90°, AB=AC,∴△ ABC为等腰直角三角形,∠ EBD=45°.∵点 D为 BC的中点,1∴AD=2BC=BD,∠ FAD= 45°.∵∠ BDE+∠ EDA=90°,∠ EDA+∠ ADF=90°,∴∠ BDE=∠ ADF.在△ BDE和△ ADF中,∠EBD=∠ FADBD=AD,∠BDE=∠ ADF∴△ BDE≌△ ADF(A S A),∴ BE=AF.(2)解:BE=AF,证明以下:连结 AD,如解图②所示 .第 5 题解图②∵∠ ABD=∠ BAD=45°,∴∠ EBD=∠ FAD=135°.∵∠ EDB+∠ BDF=90°,∠ BDF+∠ FDA=90°,∴∠ EDB=∠ FDA.在△ EDB和△ FDA中,∠EBD=∠ FADBD=AD,∠EDB=∠ FDA∴△ EDB≌△ FDA(A S A),∴ BE=AF.。

第4课时全等三角形基础达标训练1. 如图,在△ABC和△DEF中,AB=DE,∠B=∠D E F,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )A.∠A=∠DB. ∠ACB=∠DFEC. AC=DFD. BE=CF第1题图2. 如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )A. 4B. 6C. 5D. 无法确定第2题图3. 已知△ABC与△DEF全等,∠A=∠D=70°,∠B=60°,则∠F的度数是( )A. 50°B. 60°C. 60°或50°D. 70°或50°4. (2016泰安)如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )A. 44°B. 66°C. 88°D. 92°第4题图5. 如图,在△ABC中,点D在BC上,且AB=AD,AC=AE,∠BAD=∠CAE,DE=12,CD=4,则BD=________.第5题图6. (2016南京)如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC,其中所有正确结论的序号是________.第6题图7. (2016济宁)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当条件:__________,使△AEH≌△CEB.第7题图8. (2017郴州)已知△ABC中,∠ABC=∠ACB,点D、E分别为边AB、AC的中点.求证:BE=CD.第8题图9. (2016昆明)如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.求证:AE =CE.第9题图10. (2016河北改编)如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,添加一个条件:________,使得△ABC≌△DEF,并证明.第10题图11. (2017苏州)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.(1)求证:△AEC≌△BED;(2)若∠1=42°,求∠BDE的度数.第11题图12. (2017齐齐哈尔改编)如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC.E,F分别是BG,AC的中点.不添加字母及辅助线,写出图中的全等三角形,并选其中一对证明.第12题图能力提升拓展1. 如图,已知AB=12,AB⊥BC于点B,AB⊥AD于点A,AD=5,BC=10,点E是CD的中点,则AE 的长为( )A. 6B. 132C. 5D. 3241第1题图2. (2015泰州)如图,△ABC 中,AB =AC ,D 是BC 的中点,AC 的垂直平分线分别交AC 、AD 、AB 于点E 、O 、F ,则图中全等三角形的对数是( )A. 1对B. 2对C. 3对D. 4对第2题图3. (2017荆门)已知:如图,在Rt △ACB 中,∠ACB =90°,点D 是AB 的中点,点E 是CD 的中点,过点C 作CF ∥AB 交AE 的延长线于点F .(1)求证:△ADE ≌△FCE ;(2)若∠DCF =120°,DE =2,求BC 的长.第3题图4. (2017常州)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.第4题图答案基础达标训练1. D 【解析】∠B的两边是AB、BC,∠DEF的两边是DE、EF,而BC=BE+EC,EF =EC+CF,要使BC=EF,则BE=CF.2. A 【解析】∵△ABC≌△BAD,∴BC=AD=4.3. C 【解析】当△ABC≌△DFE时,∠A=∠D=70°,∠F=∠B=60°;当△ABC≌△DEF时,∠A=∠D=70°,∠B=∠E=60°,则∠F=∠C=180°-70°-60°=50°,综上所述,∠F的度数为60°或50°.4. D 【解析】∵PA=PB,∴∠A=∠B,∵AM=BK,AK=BN,∴△AMK≌△BKN(SAS),∴∠BKN=∠AMK,∵∠MKB=∠MKN+∠BKN=∠AMK+∠A,∴∠A=∠MKN=44°,∴∠P=180°-∠A-∠B=180°-2∠A=92°.5. 8【解析】∵∠BAD=∠CAE,∴∠BAC=∠DAE,在△BAC和△DAE中,=BAC DAE AC AE BA DA ∠∠==⎧⎪⎨⎪⎩,∴△BAC ≌△DAE (SAS),∴BC =DE =12,∵CD =4,∴BD =BC -DC =12-4=8.6. ①②③ 【解析】∵△ABO ≌△ADO ,∴∠AOB =∠AOD =90°,∴AC ⊥BD ,故①正确;∵△ABO ≌△ADO ,∴BO =OD ,由①知AC ⊥BD ,∴CB =CD ,故②正确;∵△ABO ≌△ADO ,∴AB =AD ,在△ABC 和△ADC 中,AB =AD ,CB =CD ,AC =AC ,∴△ABC ≌△ADC (SSS),故③正确;∵由已知不能得到DA 和DC 相等,故④不正确.综上所述,结论正确的序号是①②③.7. AH =CB (或EH =EB 或AE =CE )(只要符合要求即可)【解析】∵AD ⊥BC ,CE ⊥AB ,垂足分别为点D 、E ,∴∠ADC =∠BEC =∠AEC =90°,∴∠EAH +∠AHE =90°,∠DCH +∠CHD =90°,又∵∠AHE =∠CHD ,∴∠EAH =∠BCE ,∴根据AAS 添加AH =CB 或EH =EB ;根据ASA 添加AE =CE 即可证得△AEH ≌△CEB.故答案填:AH =CB 或EH =EB 或AE =CE 均可.8. 证明:∵∠ABC =∠ACB , ∴AB =AC ,∵D 、E 分别为边AB 、AC 的中点, ∴BD =12AB ,CE =12AC ,∴BD =CE ,又∵∠ABC =∠ACB ,BC =CB , ∴△CBE ≌△BCD (SAS), ∴BE =CD .9. 证明:∵FC ∥AB , ∴∠A =∠ECF ,新人教部编版初高中精选试题在△ADE 和△CFE 中,==A ECF AED CEF DE FE ∠∠∠∠=⎧⎪⎨⎪⎩, ∴△ADE ≌△CFE (AAS), ∴AE =CE .10. 解:BF =EC 或∠A =∠D .证明:(以下两种全等证明任选其一即可.) ①当BF =EC 时,则BF +FC =FC +EC ,即BC =EF , 在△ABC 和△DEF 中,AC DF B E DE F AB C ===⎧⎪⎨⎪⎩, ∴△ABC ≌△DEF (SSS). ②当∠A =∠D 时, 在△ABC 和△DEF 中,=A D A E C D DF AB ∠∠==⎧⎪⎨⎪⎩, ∴△ABC ≌△DEF (SAS).11. (1)证明:∵AE 和BD 相交于点O , ∴∠AOD =∠BOE ,在△AOD 和△BOE 中,∠A =∠B , ∴∠BEO =∠2,新人教部编版初高中精选试题又∵∠1=∠2, ∴∠1=∠BEO , ∴∠AE C =∠BED , 在△AEC 和△BED 中,==A B AE BEAEC BED ⎧∠∠=∠∠⎪⎨⎪⎩, ∴△AEC ≌△BED (ASA); (2)解:由(1)得△AEC ≌△BED , ∴EC =ED ,∠C =∠BDE ,∴∠C =∠EDC =12(180°-∠1)=12(180°-42°)=69°,∴∠BDE =∠C =69°.12. 解:△BDG ≌△ADC ,△BDE ≌△ADF , △EDG ≌△FDC .证明:(以下三种全等证明任选其一即可.) ①∵AD ⊥BC ,∴∠ADB =∠ADC =90°, 在△BDG 与△ADC 中,=BDG ADC DG DC BD AD∠∠==⎧⎪⎨⎪⎩, ∴△BDG ≌△ADC (SAS).②由①中△BDG ≌△ADC 可得BG =AC ,∵∠GDB =∠ADC =90°,E ,F 分别是BG ,AC 的中点,新人教部编版初高中精选试题∴BE =DE =EG =12BG ,AF =DF =CF =12AC ,∴BE =AF ,DE =DF , 在△BDE 和△ADF 中,=BE AF DE DF BD AD ==⎧⎪⎨⎪⎩, ∴△BDE ≌△ADF (SSS). ③由②得DE =DF =EG =FC , 由①得DG =DC , 在△EDG 和△FDC 中,=DE DF DG DC EG FC ==⎧⎪⎨⎪⎩, ∴△EDG ≌△FDC (SSS). 能力提升拓展1. B 【解析】如解图,延长AE 交BC 于F ,∵AB ⊥BC ,AB ⊥AD ,∴AD ∥BC ,∴∠D=∠C ,∵点E 是CD 的中点,∴DE =CE ,在△ADE 和△FCE 中,==D CAE DE CED FEC ∠∠∠∠⎧⎪=⎨⎪⎩,∴△ADE ≌△FCE (ASA),∴AE =FE ,CF =AD =5,∴BF =BC -CF =5,在Rt △ABF 中,AF =AB 2+BF2=122+52=13,∴AE =12AF =132.第1题解图2. D 【解析】∵AB =AC ,D 为BC 中点,∴CD =BD ,∠BDO =∠CDO =90°,在△ABD和△ACD 中,==AB ACBD CD AD AD⎧⎪=⎨⎪⎩,∴△ABD ≌ △ACD (SSS);∵EF 垂直平分AC ,∴OA =OC ,AE =CE ,在△AOE 和△COE 中,==OA OC AE CE OE OE⎧⎪=⎨⎪⎩,∴△AOE ≌△COE (SSS);在△BOD 和△COD 中,===BD CD BDO CDOOD OD ∠∠⎧⎪⎨⎪⎩,∴△BOD ≌△COD (SAS);由△BOD ≌△COD 可知OB =OC ,在△AOC 和△AOB 中,==AC ABOC OB OA OA⎧⎪=⎨⎪⎩,∴ △AOC ≌△AOB (SSS).综上所述,共有4对全等的三角形.3. (1)证明:∵点E 是CD 的中点,∴DE =CE ,∵AB ∥CF ,∴∠BAF =∠AFC ,在△ADE 与△FCE 中,===DAE CFE AED FECDE CE ∠∠∠∠⎧⎪⎨⎪⎩, ∴△ADE ≌△FCE (AAS);(2)解:由(1)知CD =2DE ,∴CD =4,∵CF ∥AB ,∠DCF =120°,∴∠BDC =60°,在Rt △ABC 中,D 为AB 的中点,∴CD =AD =BD ,∴△BCD 是等边三角形,∴BC =DC =4.4.(1)证明:∵∠BCE =∠ACD =90°,∠BCE =∠ACB +∠ACE ,∠ACD =∠ACE +∠DCE , ∴∠ACB =∠DCE ,在△ABC 和△DEC 中,===ACB DCE BAC DBC EC ∠∠∠∠⎧⎪⎨⎪⎩, ∴△ABC ≌△DEC (AAS),∴AC =CD ;(2)解:由(1)知AC =CD ,又∵∠ACD =90°,∴∠CAD =45°,∵AC =AE ,∴∠ACE =∠AEC =12×(180°-45°)=67.5°.∴∠DEC =180°-67.5°=112.5°.。

第4课时全等三角形基础达标训练1. 如图,在△ABC和△DEF中,AB=DE,∠B=∠D E F,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )A.∠A=∠DB. ∠ACB=∠DFEC. AC=DFD. BE=CF第1题图2. 如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )A. 4B. 6C. 5D. 无法确定第2题图3. 已知△ABC与△DEF全等,∠A=∠D=70°,∠B=60°,则∠F的度数是( )A. 50°B. 60°C. 60°或50°D. 70°或50°4. (2016泰安)如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )A. 44°B. 66°C. 88°D. 92°第4题图5. 如图,在△ABC中,点D在BC上,且AB=AD,AC=AE,∠BAD=∠CAE,DE=12,CD=4,则BD=________.第5题图6. (2016南京)如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC,其中所有正确结论的序号是________.第6题图7. (2016济宁)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当条件:__________,使△AEH≌△CEB.第7题图8. (2017郴州)已知△ABC中,∠ABC=∠ACB,点D、E分别为边AB、AC的中点.求证:BE=CD.第8题图9. (2016昆明)如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.求证:AE =CE.第9题图10. (2016河北改编)如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,添加一个条件:________,使得△ABC≌△DEF,并证明.第10题图11. (2017苏州)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.(1)求证:△AEC≌△BED;(2)若∠1=42°,求∠BDE的度数.第11题图12. (2017齐齐哈尔改编)如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC.E,F分别是BG,AC的中点.不添加字母及辅助线,写出图中的全等三角形,并选其中一对证明.第12题图能力提升拓展1. 如图,已知AB=12,AB⊥BC于点B,AB⊥AD于点A,AD=5,BC=10,点E是CD的中点,则AE 的长为( )A. 6B. 132C. 5D. 3241第1题图2. (2015泰州)如图,△ABC 中,AB =AC ,D 是BC 的中点,AC 的垂直平分线分别交AC 、AD 、AB 于点E 、O 、F ,则图中全等三角形的对数是( )A. 1对B. 2对C. 3对D. 4对第2题图3. (2017荆门)已知:如图,在Rt △ACB 中,∠ACB =90°,点D 是AB 的中点,点E 是CD 的中点,过点C 作CF ∥AB 交AE 的延长线于点F .(1)求证:△ADE ≌△FCE ;(2)若∠DCF =120°,DE =2,求BC 的长.第3题图4. (2017常州)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.第4题图答案基础达标训练1. D 【解析】∠B的两边是AB、BC,∠DEF的两边是DE、EF,而BC=BE+EC,EF =EC+CF,要使BC=EF,则BE=CF.2. A 【解析】∵△ABC≌△BAD,∴BC=AD=4.3. C 【解析】当△ABC≌△DFE时,∠A=∠D=70°,∠F=∠B=60°;当△ABC≌△DEF时,∠A=∠D=70°,∠B=∠E=60°,则∠F=∠C=180°-70°-60°=50°,综上所述,∠F的度数为60°或50°.4. D 【解析】∵PA=PB,∴∠A=∠B,∵AM=BK,AK=BN,∴△AMK≌△BKN(SAS),∴∠BKN=∠AMK,∵∠MKB=∠MKN+∠BKN=∠AMK+∠A,∴∠A=∠MKN=44°,∴∠P=180°-∠A-∠B=180°-2∠A=92°.5. 8【解析】∵∠BAD=∠CAE,∴∠BAC=∠DAE,在△BAC和△DAE中,=BAC DAE AC AE BA DA ∠∠==⎧⎪⎨⎪⎩,∴△BAC ≌△DAE (SAS),∴BC =DE =12,∵CD =4,∴BD =BC -DC =12-4=8.6. ①②③ 【解析】∵△ABO ≌△ADO ,∴∠AOB =∠AOD =90°,∴AC ⊥BD ,故①正确;∵△ABO ≌△ADO ,∴BO =OD ,由①知AC ⊥BD ,∴CB =CD ,故②正确;∵△ABO ≌△ADO ,∴AB =AD ,在△ABC 和△ADC 中,AB =AD ,CB =CD ,AC =AC ,∴△ABC ≌△ADC (SSS),故③正确;∵由已知不能得到DA 和DC 相等,故④不正确.综上所述,结论正确的序号是①②③.7. AH =CB (或EH =EB 或AE =CE )(只要符合要求即可)【解析】∵AD ⊥BC ,CE ⊥AB ,垂足分别为点D 、E ,∴∠ADC =∠BEC =∠AEC =90°,∴∠EAH +∠AHE =90°,∠DCH +∠CHD =90°,又∵∠AHE =∠CHD ,∴∠EAH =∠BCE ,∴根据AAS 添加AH =CB 或EH =EB ;根据ASA 添加AE =CE 即可证得△AEH ≌△CEB.故答案填:AH =CB 或EH =EB 或AE =CE 均可.8. 证明:∵∠ABC =∠ACB , ∴AB =AC ,∵D 、E 分别为边AB 、AC 的中点, ∴BD =12AB ,CE =12AC ,∴BD =CE ,又∵∠ABC =∠ACB ,BC =CB , ∴△CBE ≌△BCD (SAS), ∴BE =CD .9. 证明:∵FC ∥AB , ∴∠A =∠ECF ,在△ADE 和△CFE 中,==A ECF AED CEF DE FE ∠∠∠∠=⎧⎪⎨⎪⎩, ∴△ADE ≌△CFE (AAS), ∴AE =CE .10. 解:BF =EC 或∠A =∠D .证明:(以下两种全等证明任选其一即可.) ①当BF =EC 时,则BF +FC =FC +EC ,即BC =EF , 在△ABC 和△DEF 中,AC DF B E DE F AB C ===⎧⎪⎨⎪⎩, ∴△ABC ≌△DEF (SSS). ②当∠A =∠D 时, 在△ABC 和△DEF 中,=A D A E C D DF AB ∠∠==⎧⎪⎨⎪⎩, ∴△ABC ≌△DEF (SAS).11. (1)证明:∵AE 和BD 相交于点O , ∴∠AOD =∠BOE ,在△AOD 和△BOE 中,∠A =∠B , ∴∠BEO =∠2,又∵∠1=∠2, ∴∠1=∠BEO , ∴∠AE C =∠BED , 在△AEC 和△BED 中,==A B AE BEAEC BED ⎧∠∠=∠∠⎪⎨⎪⎩, ∴△AEC ≌△BED (ASA); (2)解:由(1)得△AEC ≌△BED , ∴EC =ED ,∠C =∠BDE ,∴∠C =∠EDC =12(180°-∠1)=12(180°-42°)=69°,∴∠BDE =∠C =69°.12. 解:△BDG ≌△ADC ,△BDE ≌△ADF , △EDG ≌△FDC .证明:(以下三种全等证明任选其一即可.) ①∵AD ⊥BC ,∴∠ADB =∠ADC =90°, 在△BDG 与△ADC 中,=BDG ADC DG DC BD AD∠∠==⎧⎪⎨⎪⎩, ∴△BDG ≌△ADC (SAS).②由①中△BDG ≌△ADC 可得BG =AC ,∵∠GDB =∠ADC =90°,E ,F 分别是BG ,AC 的中点,∴BE =DE =EG =12BG ,AF =DF =CF =12AC ,∴BE =AF ,DE =DF , 在△BDE 和△ADF 中,=BE AF DE DF BD AD ==⎧⎪⎨⎪⎩, ∴△BDE ≌△ADF (SSS). ③由②得DE =DF =EG =FC , 由①得DG =DC , 在△EDG 和△FDC 中,=DE DF DG DC EG FC ==⎧⎪⎨⎪⎩, ∴△EDG ≌△FDC (SSS). 能力提升拓展1. B 【解析】如解图,延长AE 交BC 于F ,∵AB ⊥BC ,AB ⊥AD ,∴AD ∥BC ,∴∠D=∠C ,∵点E 是CD 的中点,∴DE =CE ,在△ADE 和△FCE 中,==D CAE DE CE D FEC ∠∠∠∠⎧⎪=⎨⎪⎩,∴△ADE ≌△FCE (ASA),∴AE =FE ,CF =AD =5,∴BF =BC -CF =5,在Rt △ABF 中,AF =AB 2+BF2=122+52=13,∴AE =12AF =132.第1题解图2. D 【解析】∵AB =AC ,D 为BC 中点,∴CD =BD ,∠BDO =∠CDO =90°,在△ABD和△ACD 中,==AB ACBD CD AD AD ⎧⎪=⎨⎪⎩,∴△ABD ≌ △ACD (SSS);∵EF 垂直平分AC ,∴OA =OC ,AE =CE ,在△AOE 和△COE 中,==OA OC AE CE OE OE⎧⎪=⎨⎪⎩,∴△AOE ≌△COE (SSS);在△BOD 和△COD 中,===BD CD BDO CDOOD OD ∠∠⎧⎪⎨⎪⎩,∴△BOD ≌△COD (SAS);由△BOD ≌△COD 可知OB =OC ,在△AOC 和△AOB 中,==AC ABOC OB OA OA ⎧⎪=⎨⎪⎩,∴ △AOC ≌△AOB (SSS).综上所述,共有4对全等的三角形.3. (1)证明:∵点E 是CD 的中点,∴DE =CE ,∵AB ∥CF ,∴∠BAF =∠AFC ,在△ADE 与△FCE 中,===DAE CFE AED FECDE CE ∠∠∠∠⎧⎪⎨⎪⎩, ∴△ADE ≌△FCE (AAS);(2)解:由(1)知CD =2DE ,∴CD =4,∵CF ∥AB ,∠DCF =120°,∴∠BDC =60°,在Rt △ABC 中,D 为AB 的中点,∴CD =AD =BD ,∴△BCD 是等边三角形,∴BC =DC =4.4.(1)证明:∵∠BCE =∠ACD =90°,∠BCE =∠ACB +∠ACE ,∠ACD =∠ACE +∠DCE , ∴∠ACB =∠DCE ,在△ABC 和△DEC 中,===ACB DCE BAC DBC EC ∠∠∠∠⎧⎪⎨⎪⎩, ∴△ABC ≌△DEC (AAS),∴AC =CD ;(2)解:由(1)知AC =CD ,又∵∠ACD =90°,∴∠CAD =45°,∵AC =AE ,∴∠ACE =∠AEC =12×(180°-45°)=67.5°. ∴∠DEC =180°-67.5°=112.5°.。