当前位置：文档之家 › 晶格振动PPT课件

晶格振动PPT课件

  • 格式：ppt
  • 大小：2.09 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

第三章晶格振动和晶体的热学性质PPT

第三章晶格振动和晶体的热学性质PPT

(3)周期性边界条件、第一布里渊区中的模数
a
波恩-卡门边界条件
（周期性边界条件）
a
q的取值采用波恩-卡门边界条件（周期性边界条件）来定：
u1 u N 1
N为晶格中的原子个数（晶胞数 ）
即：
Ae Ae i(qat)
i[q( N 1)at ]
un Ae i(qnat)
u1 u N 1
Ae Ae i(qat)
i[q( N 1)at ]
eiqNa 1
得： qNa 2l l =0，±1，±2……等整数
q 2 l
Na
在第一布里渊区，q取值为
/a q /a
对应于 N / 2l N / 2 ( 只l 能取N个值----模数 )
结论：在第一布里渊区内的q值唯一地描述了所有的晶格 振动模式，这些值的数目等于晶格的自由度数N。
设 un,1、u是n,相2 应于原子M、m在沿链方向对其平衡位置的偏离
方程和解
和单原子链类似，若只考虑最近邻原子的相互作用，则有：
Mun,1 2un,1 un,2 un1,2 mun,2 2un,2 un1,1 un,1
类似于前面的讨论，可取解的形式为：
代入运动方程得：
(2 m 2 )A (2 cos qa)B 0
2 cos qa
2
2
2 M 2
0
Mm 4
2
(M
m) 2
4
2
sin 2
1 2
qa
0
Mm 4
2 (M
m) 2
4
2
sin 2
1 2
qa
0
解关于2的一元二次方程得：
2
(q)
mM mM

s第04章晶格振动PPT课件

s第04章晶格振动PPT课件

在3r支色散关系中，当q→0时（长波）：
➢ 有三支ω →0，且各原子的振幅趋于相同， 这三支为声学波。长声学波描述了原胞质 心的振动。
➢ 其余(3r-3)支有有限的振动频率，为光学 波。长光学波描述原胞内原子之间的相对 运动。
波矢的取值和波矢空间
q的值由周期性边界条件确定：
u
Rl
N1a1
s
u
Rl s
u
Rl
N2a2
s
u
Rl s
代入 u
l s
A ei(q•Rl t ) sa
得到：
u
Rl
N3a3
s
u
Rl s
q • N1a1 2h1, q • N2a2 2h2 , q • N3a3 2h3
把波矢q表示为倒格子空间中的一 个矢量： q x1b1 x2b2 x3b3
光学波
在布里渊区边界 q
a
声学波： A
B
光学波： A 0
B
5、振动模式数（频率数）
波矢限定在第一布里渊区中 q
a
a
周期性边界条件下
q 2 l
Na
N l N
2
2
一维双原子链：
晶格振动的波矢数目等于晶体的原胞数
一个波矢对应2个不同的频率，共有2N个振动频 率，这2N个振动频率分为2支。
f
d
d
(un1 un )
→弹性力
一维原子链的振动模型：被一个个弹簧连接 起来的一串质量为m的球
第n个原子受到的作用力为：
f p (un p un )
p
p 1， 2， 3，
2、一维单原子链的运动方程
f p (xn p xn )

第三章晶格振动与晶体的热学性质PPT课件

第三章晶格振动与晶体的热学性质PPT课件

4ed
0
e
2
1
CV 1254NkBTD3T3
德拜 T3 定律 ：CV 与 T3 成比例
注意：T3 定律一般只适用于大约
1 T 30 D
的范围
这表明，Debye模型可以很好地解释在很低 温度下晶格热容CV∝ T3的实验结果。
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
的色散关系，称为晶格振动的振动谱。 (q )
利用波与格波的相互作用，以实验的方法直接
测定 (q)
一、格波振动使中子流的非弹性散射 二、（可见光）光子与晶格的非弹性散射 三、X光的非弹性散射
只讨论单声子过程
因而，光散射只能和长波声子，即接近布里渊区 心的声子发生相互作用。
用可见光散射方法只能测定原点附近的很小一 部分长波声子的振动谱，而不能测定整个晶格振 动谱，这是光可见散射法的最根本缺点。
<<1
(1)★ 声学波
2m m M M 11m 4 m M M 2si2n aq 1/2
2m m M M 11m 4 mM M2sin2aq1/2
简化
m4mMM2sin2aq1 1m 4 m M 2 M si2a n 1 q /2 11 2m 4 m M 2 M si2a nq
32
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal

最新2019-三维晶格的振动-PPT课件

最新2019-三维晶格的振动-PPT课件

分布密度＝
1

b1 N1

b2 N2

b3 N3

N v0 (2 )3

V (2
)3
V 为晶体 的体积
从原子振动考查, q 的作用只在于确定不同原胞之间 振动位相的联系, 具体表现在格波解中的位相因子
ei R(l )q
如果 q 改变一个倒格子矢量 G n n 1 b 1 n 2 b 2 n 3 b 3 ,
由于边界条件允许的 q 分布密度为 V/(2π)³, 因此不同 q 的总数应当是
(倒 格 子 原 胞 体 积 ） V /(2)3 N
和晶体中包含的原胞数目相同. 对于每个 q 有 3 个
声学波, (3n－3) 个光学波, 所以不同的格波的总数是
N(33n3) 3nN
正好等于晶体 Nn 个原子的自由度。这表明, 上述的格波已概括了晶体的全部振动模
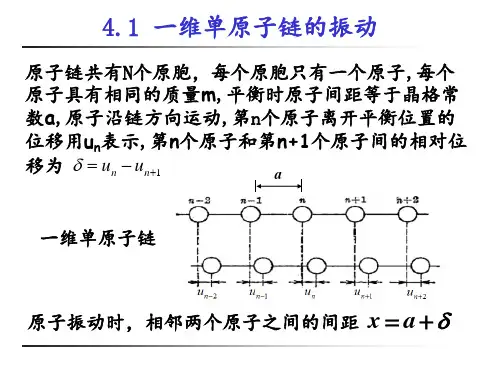
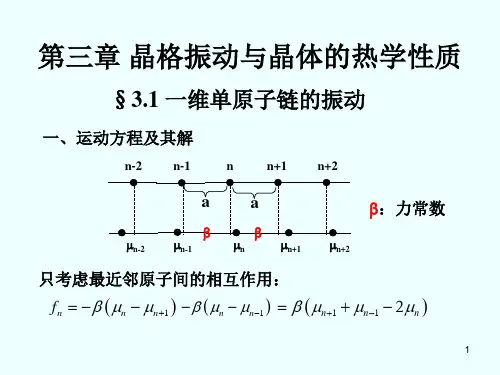
边界条件表示, 沿着 ai 方向, 原胞的标 数增加 Ni , 振动情况必须相同 (i=1,2,3)
边界条件要求
q N 1 a 1 h1 2 ,
x1

h1 N1
q N 2 a 2 h2 2 ,
x2

h2 N2
q N 3 a 3 h3 2 ,
q

指数函数表示各种原子的振动都具有共同的平面 波的形式, q 是其波数矢量
A1 (A1x, A1y, A1z), A2 (A2x, A2y, A2z), …可以是复数, 表示各原子的位移分量的振幅和位相可以有区别
上式实际上表示了三维晶格格波的一般形式
同样可证明, 代回运动方程后, 得到以 A1x , A1y , A1z , …, Anx , Any , Anz 为未知数的 3n 个线性齐次联立方程

固体物理--第三章 晶格振动ppt课件

固体物理--第三章 晶格振动ppt课件

5
2a
2
q2 q1 a
5
三、周期性边界条件（Born－Karman边界条件）
N+1
12
n
N N+2 N+n
N n
n
Aeit N naq Aeitnaq
eiNaq 1 ei2h 1
q 2 h
Na
h =整数
6
在q轴上，每一个q的取值所占的空间为 2
Na
q的分布密度：
q Na L
子数不守恒。
11
§3.2 一维双原子链的振动
考虑由P、Q两种原子等距相间排列的一维双原子链
一、运动方程及其解
a Mm
{
n-1 n n n+1
只考虑近邻原子间的弹性相互作用
{ 运动方程：
M n n n1 2n
m n n n1 2 n
试 解：
it naq
Ae n
{ Bei
q 0
光波： ＝c0q， c0为光速
对于实际晶体， ＋(0)在1013 ~ 1014Hz，对应于远 红外光范围。离子晶体中光学波的共振可引起对远红外 光在 ＋(0)附近的强烈吸收。
18
2. 声学波（acoustic branch）
n n
M
m
2m
cos
1 2
aqei
12aq
M 2 m2 2Mm cosaq
2 2
L＝Na ——晶体链的长度
简约区中波数q的取值总数 q 2 Na 2
a 2 a
＝N＝晶体链的原胞数
晶格振动格波的总数=N·1 =晶体链的自由度数
7
四、格波的简谐性、声子概念
晶体链的动能：

第04章晶格振动

第04章晶格振动
U(a)：平衡时两个原子
r 之间的相互作用势能
U(a ) ：有相对位移时
f
两个原子之间的相互作
r
用势能
R0
简谐近似
恢复力常数
微振动时，有：
U(x)

U a



U a

dU dx

a

1 2

d2 U d x2

a
2

简谐近似：势能展开式保留到二次项：
l l
s
u


s

恢复力常数
一个原胞中有3n个类似的方程,N个原胞共有3nN个
方程的解和一维原子链类似，可以写成:
u

l s



A e i(qRl t ) sa
三维晶格的振动
把试探解代入运动方程，得到以振幅Asa满足的3n个 线性齐次联立方程：

M
2 2

2M1M2
c os qa
12


M1 M2 M1M2
1

1


4M1M2 (M1 M2 )2
sin2
(
1 2
qa)

12
与单原子链的色散关系明显不同之处在于,双原
子链每个波矢q对应两个不同频率的格波：
声学波
2

三维晶格的振动
在3n支色散关系中，当q→0时（长波）： 有三支ω →0，且各原子的振幅趋于相 同，这三支为声学波。长声学波描述了 不同原胞之间的相对运动
其余3n－3支有有限的振动频率，为光 学波。长光学波描述n个格子之间的相 对振动。

第四章 晶格振动优秀PPT

第四章 晶格振动优秀PPT
lkAkei[tRlkq]
将方程解代回3n个运动方程
—— 3n个线性齐次方程 m k2Akk'Ck q,k'Ak'
m in00
m a x /2 a 2 k /M
光学波
m in /2 a 2 k/m
m a x 0 2 k m M /m M
声学波
A B
2kcosqa
2km2
0
相邻异类原子一般朝同一方向振动
在长波极限：相邻原子同向振动，而且振幅 相同，它们的振动(波动)行为好象是同一类原 子。反映的是晶格的整体振动 。
光学波
A B
2kcosqa
2km2
0
相邻异类原子一般朝相反方向振动
q0
在长波极限：A/B
M/m,
mA+MB=0，
晶胞质心不动。晶体并非整体呈刚体，其中
的轻原子与重原子分别构成刚性结构，而且
两类原子永远反向振动。
与一维单原子链主要结论的比较
共同特点：色散关系中，角频率都为波矢的周 期函数，都有极值。波矢都只能取分离的值， 取值数目都为晶体原胞的个数。 不同之处：
—— 一个格波表示的是所有原子同时做频率为 的振动
➢ 差别：格波的空间坐标是离散的。
➢联系：在长波极限下，常用连续介质弹性波代替
较复杂的格波。（证明）
例1
证明在长波极限下，可用连续介质弹性波代 替较复杂的格波。
2
k m
sin
qa 2
q0
a
k m
q
vq
v ka ，而Y ka， m a
m/a
u Aei[(n1)aqt] n1
格波
u Aei[(n1)aqt] n1

第4章 晶格振动

第4章 晶格振动

(
2π
a
− q)sa − ω
t
same as k= − q
= A exp[i(2π s − qsa − ω t)] = A exp[i(− qsa − ω t)]
λ=4a/3
λ=4a/7
λ=4a
λ1 = 4a,
λ2
=
4a 3
,
λ3 =
4a 5
,
λ4
=
4a 7
,
k1
=
2π 4a
=
π 2a
0.8
0.6
0.4
0.2
0.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
k [(2π /a) m-1]
For a small k (ka<<1) Long wavelength limit
ω≈
4C M
ka 2
=
C M
a k =
Ca M/a
k=
Ca k
λ
= vk continuum elastic wave limit
ω2
=
2C M
(1− cos(ka)) =
2C M

2
sin
2
(
ka 2
)

ω=
4C M
sin
ka 2
Dispersion relation
When k =
4C
±
π
a
ω= M
: maximum
set the boundary of first BZ
ω [(4C/M)1/2 sec-1]
1.0

第三章晶格振动1PPT课件

第三章晶格振动1PPT课件
在简谐近似下，我们实际处理的是晶格振动的低激发态问 题，晶格振动由简正模描述，这个简正模就是声子 （Phonon）。由此，我们把晶格振动这个多体问题转化为 单体问题，即对声子的描述。而非简谐项(Anharmonic term) 可以用涉及声子的相互作用来解决。如晶格热导率涉及声 子碰撞。
5.1 一维单原子链的振动
一、运动方程及其解
n-2 n-1 n n+1 n+2Βιβλιοθήκη 考虑由一同种原子组成的一维
a
单原子链的振动。设平衡时相邻
原子间距为a（即原胞大小），在 t 时刻第n个原子偏离其平衡位置
n-2 n-1
n
n+1 n+2
的位移为n，如只考虑最近邻原子间的弹性相互作用，有
f n n n 1 n n 1 n 1 n 1 2 n
把薛定谔方程分离变量得：
V T ( n R ) V ( V R n )( R m ( ) R ) n ( r ( ,R R ) n )V e( r n ,R ) V e( r n ,R n )( r ,R n ) d r
其中V(r)是离子实之间的相互作用势。除去离子实之间的库 仑相互作用外，还有电子的贡献
一个原子实静态的模型无法解释如下几种现象
1. 无法解释晶体的比热等一系列晶体平衡态物性 2. 无法解释电导等一系列输运特性 3. 无法解释固体同各种辐射波的相互作用
晶体平衡态物性：
比热：晶体中电子的比热与晶体实际比热差别非常大。同时， 按照经典热力学对晶体比热的估算也在低温段失效。
热膨胀系数：只是电子引起的变化不足以理解晶体的膨胀系 数。
其中为弹性恢复力系数。设原子质量为m，则第n个原
子的运动方程为 m n 1 n 1 2 n
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
16
德拜温度ΘD往往由实验确定，使在不同的温
度下，晶格热容CV的理论值与实验值相符，从而确
定ΘD。
17
• 实验和理论的比较
高温情况：固体实际热容和爱因斯坦模型比较
爱因斯坦模型热容表示式（3-71）中：
eE
e E T
T
1 2

1E / E /T
T
2


T
E
2
谐振子。根据经典理论的能量均分定理，每个简谐振
子的平均能量为kBT(kB为玻耳兹曼常数)，因而总晶
格振动能为：
相应的热容为：
U＝3NSkBT
CV＝3NSkB
CV,m=3NAkB=3R 5
其中，NA为阿伏伽德罗常数。摩尔热容与材料的
性质及温度无关，符合杜隆—泊替定律。固体热容在
低温下正比于T3是经典物理无法解释的难题。
10
• 爱因斯坦模型
假定晶体中所有原子都以相同频率独立地振动，则
晶体中的格波频率都相同。NS个原子组成的晶体
U T ＝3NS E(
,T
)＝3NS


1 2

e
1
kBT

1
则热容CV为：
（3-69）
2
Cv＝
U T
＝3NSkB v


kBT

15
引入德拜温度ΘD，设 D kBΘD
换：
x＝
kBT
d＝ kBT dx

则式（3-73）可改写成：
，作变量代
C
v＝
3V 2 2
3 p
D T
kB4T 3
x4
0
2
e x dx ex 1 2
＝9NkB
T3 D3
D T
0
x 4e x dx
ex
2
1
（3-76）
第三章 晶格振动
§3-4 晶体的热容
• 概述
在一般温度变化范围的过程中，固体的体积变化不大，
可近似地视为定容过程。定容热容定义:单位质量的
物质在定容过程中，温度升高1℃时，系统内能的增
量，即
C

lim T 0
U T
＝ V
U T
V
Volum 1 e
晶体的运动能量包括:
曲线尽可能地与实验曲线拟合，从而确定爱因斯坦
温度ΘE。对大多数固体，ΘE在100～300K之间。
12
• 德拜模型
把晶体视为各向同性的连续弹性媒质。设晶体是N 个初基原胞组成的三维单式格子(S＝1)，晶体中仅 有3支声学支格波，并设它们的相速vp都相同。因
而三支格波的色散关系均是线性的:
ω=vpq
则等频率面（等能面）为球面：
e / kBT e / kBT 1 2
（3-70）
11
式中的频率ω还是个待定的量。为了确定ω，引入 爱因斯坦温度ΘE，定义：
E kBE
则热容成为ΘE和温度T的函数：
2
Cv＝3NSkB

E T

eE /T
e E T
2
1
（3-71）
在声子热容CV显著变化的温度范围内，使热容理论
则定容热容为：
C＝
U T
＝ V T
m
0
gE,T d
8
把式（3-58′）代入上式，得到
C＝
m 0
kB


kBT
2

e kBT e kBT－1
2
g

d
（3-68）
格波态密度函数：
3s
g ＝
晶格振动能量Ul (Lattice) 电子运动能量Ue (Electron) 对热容的贡献分别用晶格热容CVl 和电子热容 CVe来表示。除极低温下金属中的电子热容相对较大， 通常CVl＞＞CVe，故晶格热容CVl简化为CV。
2
固体热容的实验定律：高温下的杜隆—珀替 （Dulong
-Petit）定律和低温下的德拜（Debye）定律。
量子理论热容的计算 然而，从量子论的观点出发，每个谐振子能量都是量
子化的，其平均能量不再是kBT，而成为：
6


E ＝ 1 ＋
1

2
exp

kBT


1



1

2

n



（3-58′）
晶格振动能量为3NS个量子谐振子能量之和，晶体的
m
0
kB2


kBT
2

e kBT e kBT 1
2
d
（3-73）
14
式中，截止频率ωm又称为德拜频率，记为ωD，它
由格波总数等于3N来确定：
D
0
g

d＝ 3V
2
2
3 p

0
D

2d＝3N
求得：
（3-74）
D3

6π2N p
V
（3-75）
杜隆—珀替定律：对确定的材料，高温下的热容为常 数，摩尔热容为3R，
R=8.314510±0.000070J/(3成正比。
3
图3-19 硅、锗的热容与温度的关系
4
经典理论热容的计算
设单位质量的晶体中有NS个原子，则其自由度数为
3NS。晶体中的格波可归结为3NS个相互独立的简

主要因为高温时ΘE/T＜＜1，又当x ＜＜ 1时，
ex≈1+x，那么（3-71）成为：
CV＝3NSkB
19
若所考查的晶体为1mol 同元素的物质，则
∣qω(q)∣＝ d
dq

vp
13
由式（3-48）可得格波态密度函数：
g()

3S

i 1
gi
()
3S

i 1
V (2π)3

dS
qi (q)
3 V 4πq2 3V
(2π)3 vp 2 2v3p
代入式（3-68），得：
（3-72）
Cv＝
3V
2 2
3 p
3NS个量子谐振子与3NS个格波一一对应，晶格振动
能也就是各个格波能量之和：
U
=
3NS
Ei
i 1

3NS 1
(
i1 2
+n
) ωi
（3-67）
7
由格波态密度函数g(ω)的定义，上式可写成：
U＝0m g()E(,T )d
其中，ωm为截止频率，且有：
m g()d() 3NS 0
i 1
gi
3s
＝
i 1
V
2
3
dS
qi q
（3-68′）
9
对于具体的晶体，求解g(ω)十分困难，式（3-68） 的积分也不容易。人们经常使用简化的模型来讨论晶 体热容问题。主要包括：爱因斯坦（Einsten）模型 和德拜(Debye) 模型，均建立在谐振子能量量子化 的基础上，得出了基本正确、超越经典物理的结论。 另一方面它们又都对格波的态密度函数作了不同程度 的近似。因而结论在定量上与实验有不同程度的偏差。