[工学]电路与模拟电子技术ppt 第2章 一阶动态电路的暂态分析

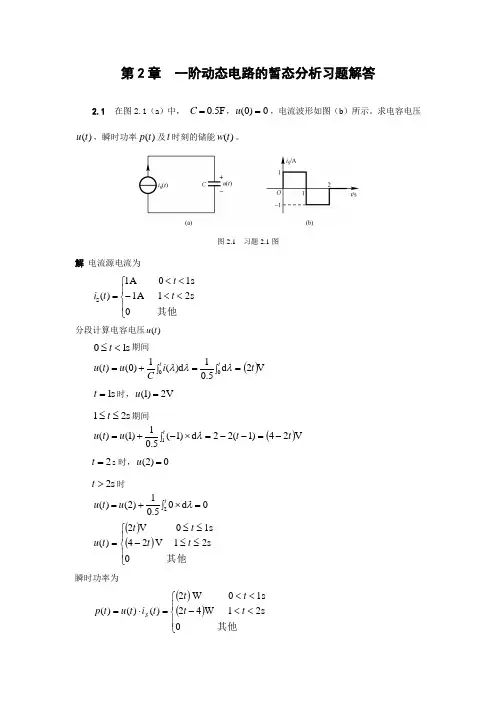
第2章 一阶动态电路的暂态分析习题解答2.1 在图2.1（a ）中， F 5.0=C ，0)0(=u ，电流波形如图（b ）所示。

求电容电压)(t u ，瞬时功率)(t p 及t 时刻的储能)(t w 。

图2.1 习题2.1图解 电流源电流为⎪⎩⎪⎨⎧<<-<<=其他 02s 11A 1s 0 1A)(S t t t i分段计算电容电压)(t us 10<≤t 期间()V 2d 5.01d )(1)0()(00⎰==⎰+=tt t i C u t u λλλs 1=t 时，V 2)1(=us 21≤≤t 期间()V 24)1(22d )1(5.01)1()(1t t u t u t-=⎰--=⨯-+=λ 2=t s 时，0)2(=u s 2>t 时⎰=⨯+=tu t u 20d 05.01)2()(λ ()()⎪⎩⎪⎨⎧≤≤-≤≤=其他 02s 1 V 241s 0V 2)(t t t t t u瞬时功率为()()⎪⎩⎪⎨⎧<<-<<=⋅=其他 02s 1W 421s 0 W2)()()(t t t t t i t u t p S电容的储能为()⎪⎪⎩⎪⎪⎨⎧<<-<<==其他 02s 1 J 21s 0 J )(21)(222t t t t t Cu t w2.2 在图2.2（a ）中，电感H 3=L ，电流波形如图（b ）所示，求电压u 、s 1=t 时电感吸收功率及储存的能量。

图2.2 习题2.2图解 由图2.2(b)可写出电流的函数()⎪⎩⎪⎨⎧≤≤-≤≤=其他 02s 1A 21s 0 A )(t t t t t i⎪⎩⎪⎨⎧<<-<<==其他 02s 1 V 31s 0 V 3)(t t dt di L t u1s =t 时3W )1()1()1(==i u p J 231321)1(21)1(22L =⨯⨯==Li w 2.3 在图2.3所示电路中，已知()V 4cos 8t t u =，()A 201=i ，()A 102=i ，求0>t 时的()t i 1 和()t i 2。

《电路与模拟电子技术基础 习题及实验指导答案 第二版》第1章 直流电路一、填 空 题1.4.1 与之联接的外电路；1.4.2 1-n ，)1(--n b ；1.4.3 不变；1.4.4 21W ，负载；1.4.5 Ω1.65A ，　； 1.4.6 1A 3A ，　； 1.4.7 3213212)(3)23(R R R R R R R +++=； 1.4.8 1A ；1.4.9 Ω4.0，A 5.12；1.4.10 电压控制电压源、电压控制电流源、电流控制电压源、电流控制电流源；1.4.11 3A ；1.4.12 3A ；1.4.13 Ω2；1.4.14 15V ，Ω5.4；1.4.15 V 6S =U 。

二、单 项 选 择 题1.4.16 C ； 1.4.17 B ； 1.4.18 D ； 1.4.19 A ；1.4.20 A ； 1.4.21 C ； 1.4.22 B ； 1.4.23 D 。

第2章一阶动态电路的暂态分析一、填 空 题2.4.1 短路，开路；2.4.2 零输入响应；2.4.3 短路，开路；2.4.4 电容电压，电感电流；2.4.5 越慢；2.4.6 换路瞬间；2.4.7 三角波；2.4.8 s 05.0，k Ω25； 2.4.9 C R R R R 3232+； 2.4.10 mA 1,V 2。

二、单 项 选 择 题2.4.11 B ； 2.4.12 D ； 2.4.13 B ；2.4.14 D ； 2.4.15 B ； 2.4.16 C 。

第3章 正弦稳态电路的分析一、填 空 题3.4.1 ︒300.02s A 10，　，　； 3.4.2 V )13.532sin(25)(︒+=t t u ；3.4.3 容性， A 44；3.4.4 10V ，2V3.4.5 相同；3.4.6 V 30，20V ；3.4.7 A 44，W 7744；3.4.8 A 5；3.4.9 减小、不变、提高；3.4.10 F 7.87μ；3.4.11 20kVA ，12kvar -；3.4.12 不变、增加、减少；3.4.13 电阻性，电容性； 3.4.14 LC π21，阻抗，电流；3.4.15 1rad/s ，4；3.4.16 Ω10；3.4.17 P L U U =，P L 3I I =，︒-30； 3.4.18 P L 3U U =，P L I I =，超前。

第
4章
一阶线性电路的暂态分析 67
图4.2.5 RC 电路的零状态响应
4.2.2 一阶动态电路暂态分析的三要素法
通过前面的分析可知，零输入响应和零状态响应可看成是全响应的特例。

直流电源激励下的一阶动态电路中的电压或电流，其全响应总是由初始值开始，按指数规律变化而接近于稳态值。

则全响应f (t )可表示为
()()[(0)()]e t
f t f f f τ−+=+−∞∞ （4.2.12）
只要知道了初始值f (0+)、稳态值f (∞)和时间常数τ 这三个要素，就可以通过式（4.2.12）直接写出直流电源激励下的一阶动态电路的全响应，这种方法称为三要素法。

时间常数 L RC R ττ⎛⎞==⎜⎟⎝
⎠或，其中R 为等效电阻，是换路后从储能元件C （或L ）两端看进去的除源网络外的入端电阻，即戴维宁或诺顿等效电路的等效电阻。

三要素法具有方便、实用和物理概念清楚等特点，是求解一阶电路常用的方法。

例4.2.1 在图4.2.6（a ）所示的电路中，U S =180 V ，R 1=30Ω，R 2=60Ω，C =100μF ，电容初始电压为0，t =0时开关S 合上。

试求换路后的u C (t )
、i
1(t
)。

图4.2.6 例4.2.1题图
解：利用三要素法求解。

（1）求初始值u C (0+)、i 1(0+)
由换路定律知
u C (0+) = u C (0-) = 0
由于u C (0+ ) = 0，此时电容可视为短路，因此有换路后t = 0+时的等效电路，如图4.2.6（b ）所示。

则有。