5电路的暂态分析PPT课件
- 格式:ppt
- 大小:2.22 MB
- 文档页数:91



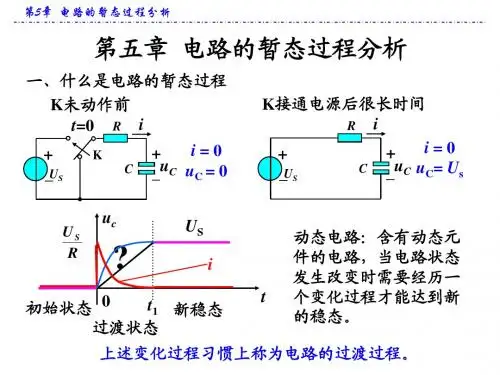
第五章电路的暂态过程分析初始状态过渡状态新稳态t 1U Su ct0?动态电路:含有动态元件的电路,当电路状态发生改变时需要经历一个变化过程才能达到新的稳态。
上述变化过程习惯上称为电路的过渡过程。
iRU SKCu C +_R i +_U S t =0一、什么是电路的暂态过程K 未动作前i = 0u C = 0i = 0u C = U s K 接通电源后很长时间C u C +_R i+_U S二、过渡过程产生的原因。
(1). 电路内部含有储能元件L 、M 、C能量的储存和释放都需要一定的时间来完成(2). 电路结构、状态发生变化支路接入或断开,参数变化(换路)三、动态电路与稳态电路的比较:换路发生后的整个变化过程动态分析微分方程的通解任意激励微分方程稳态分析换路发生很长时间后重新达到稳态微分方程的特解恒定或周期性激励代数方程一、电容元件§5-1 电容与电感元件uCi+_q i)()(t Cu t q =dtdu Cdt dq i ==任何时刻,通过电容元件的电流与该时刻的电压变化率成正比。
电荷量q 与两极之间电压的关系可用在q -u 平面上可用一条曲线表示,则称该二端元件称为电容元件。
二、电感元件+–u (t)i (t)Φ(t)N uLi+_()()()()t Li t d di t u t Ldt dtψψ===任何时刻,电感元件两端的电压与该时刻的电流变化率成正比。
Φi交链的磁通链与产生该磁通的电流的关系可用在Ψ-i 平面上可用一条曲线表示,则称该二端元件为电感元件。
§5-2 换路定则与初值的确定t = 0+与t = 0-的概念设换路在t =0时刻进行。
0-换路前一瞬间0+ 换路后一瞬间00(0)lim ()t t f f t -→<=00(0)lim ()t t f f t +→>=初始条件为t = 0+时u ,i 及其各阶导数的值。
0-0+0tf (t )基本概念:一、换路定则1()()d tC u t i C ξξ-∞=⎰0011()d ()d t i i C C ξξξξ---∞=+⎰⎰01(0)()d tC u i C ξξ--=+⎰t = 0+时刻001(0)(0)()d C C u u i C ξξ++--=+⎰当i (ξ)为有限值时u C (0+) = u C (0-)电荷守恒结论:换路瞬间,若电容电流保持为有限值,则电容电压(电荷)换路前后保持不变。




第五章电路的暂态分析第一节学习指导一、学习目的和要求1.稳态和暂态的概念2.换路定理与电压和电流初始值的确定。
3.一阶线性RC、RL电路零输入响应。
4.一阶线性RC、RL电路零状态响应。
5.一阶线性RC、RL电路全响应及三要素法求解。
6.微分电路与积分电路二、内容简介1.稳态和暂态的概念稳态是指电路中的电压和电流在给定的条件下已达到某一稳态值(对交流来讲是其幅值达到稳定)我们把直流电路、电压(电流)和呈周期性变化的交流电路称为稳态电路。
暂态是指电路在过渡过程(过渡过程的外部条件是换路即开关接通、断开,电路的参数变化,电源电压变化等。
电路产生过渡过程的根本原因系统中的能量不能发生跃变。
电路中的电场能和磁场能不能发生跃变是)中的工作状态即指两种稳定状态的中间转换过程。
2.换路定理与电压和电流初始值的确定。
(如表5-1所示)表5-1 换路定理与电压和电流初始值的确定1293.一阶线性RC、RL电路零输入响应、零状态响应、全响应及三要素法求解。
(如表5-2所示)表5-2 一阶线性RC、RL电路零输入响应、零状态响应、全响应及三要素法1301311321334.用“三要素法”求解一阶暂态电路的简要步骤如下:(1)稳态值)(∞f :取换路后的电路,将其中的电感元件视作短路,电容视作开路,获得直流电阻性电路,求出各支路电流和各元件端电压,即为它们的稳态值)(∞f 。
(2)初始值)0(+f :① 若换路前电路处于稳态,可用求稳态值的方法求出电感中的电流)0(-L i 或电容两端的电压)0(-C u ,其他元件的电压、电流可不必求解。
由换路定则有),0()0(),0()0(-+-+==L C L L u u i i 即为它们的初始值。
② 若换路前电路处于前一个暂态过程中,则可将换路时间0t 代入前一过程的)(t i L 或)(t u C 中,即得)(0-t i L 或)(0-t u C ,由换路定则有)()(00-+=t i t i L L 或)()(00-+=t u t u C C ,即为它们的初始值。


