下载文档原格式
牛顿法代数插值ndash 差商表的求法原文地址：牛顿法代数插值–差商表的求法作者：大关牛顿法代数插值–差商表的求法下面的求插商的方法并不是好的求插商的方式，因为他的效率并不是很高，不论是从空间效率还是时间效率，但是下面主要探讨的是一种将塔形的数据转换成一位数组的方式。
实际上求插商仅通过一个n个元素的一位数组就能解决，但本文强调的是一种思路，希望对大家有所借鉴。
牛顿插商公式：f[xi,xj]=(f(xj)– f(xi))/(xj– xi)f[xi,xj,xk]=(f[xj,xk]– f[xi,xj])/(xk– xi)….f[x0,x1,x2…,xn]=(f[x1,x2,…,xn]– f[x0,x1,…,xn-1])/(xn– x0)转换成均插表(或称差商表)形式如下：定义1：f[xi,xi+1,…xj]简记为f(i,j)其中i=0&&i=n&&j=0&&j=n&&i j；记f(xi)为f[xi,xi]即f(i,i)根据定义1可以推出：f[x0,x1]=f(0,1),f[x0,x1…xn]=f(0,n)….根据定义1：可以将插商表转换为如下形式。
根据上图，可以给出实际一维数组存储时的序列关系，如下图所示：此时f(0,0)位置是数组下标0，f(1,1)是数组下标为1….这样，我们从中找出相应的规律。
推论1：已知f(i,j)，n为变量的数目，令k=j– i。
当k不等于0时，f(i,j)在数组中的下标通过计算得：Index=k*n–((k-1)*k)/2+i当k等于0时Index=i。
推论1很容易证明(实际就是一个等差数列求和问题)这里证明略。
推论2：n为变量的数目，则一维数组的长度可以计算得((1+n)*n)/2推论2可以通过等差数列求和得以证明。
证明略。
推论3：各阶插商就是f(0,k)k=1,2….n.推论3：根据插商的定义和定义1可以直接推出。
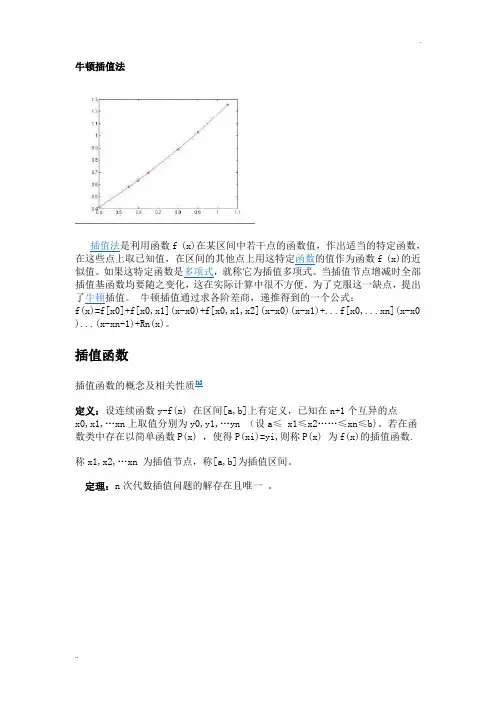
牛顿插值法插值法是利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
如果这特定函数是多项式，就称它为插值多项式。
当插值节点增减时全部插值基函数均要随之变化，这在实际计算中很不方便。
为了克服这一缺点，提出了牛顿插值。
牛顿插值通过求各阶差商，递推得到的一个公式：f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0 )...(x-xn-1)+Rn(x)。
插值函数插值函数的概念及相关性质[1]定义：设连续函数y-f(x) 在区间[a,b]上有定义，已知在n+1个互异的点x0,x1,…xn上取值分别为y0,y1,…yn （设a≤ x1≤x2……≤xn≤b)。
若在函数类中存在以简单函数P(x) ，使得P(xi)=yi,则称P(x) 为f(x)的插值函数.称x1,x2,…xn 为插值节点，称[a,b]为插值区间。
定理：n次代数插值问题的解存在且唯一。
牛顿插值法C程序程序框图#include<stdio.h>void main(){float x[11],y[11][11],xx,temp,newton;int i,j,n;printf("Newton插值:\n请输入要运算的值:x=");scanf("%f",&xx);printf("请输入插值的次数(n<11):n=");scanf("%d",&n);printf("请输入%d组值:\n",n+1);for(i=0;i<n+1;i++){ printf("x%d=",i);scanf("%f",&x[i]);printf("y%d=",i);scanf("%f",&y[0][i]);}for(i=1;i<n+1;i++)for(j=i;j<n+1;j++){ if(i>1)y[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-i]);elsey[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-1]);printf("%f\n",y[i][i]);}temp=1;newton=y[0][0];for(i=1;i<n+1;i++){ temp=temp*(xx-x[i-1]);newton=newton+y[i][i]*temp;}printf("求得的结果为:N(%.4f)=%9f\n",xx,newton);牛顿插值法Matlab程序function f = Newton(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等！');return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f); %将插值多项式展开f = vpa(f, 6);endend牛顿插值法摘要：值法利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
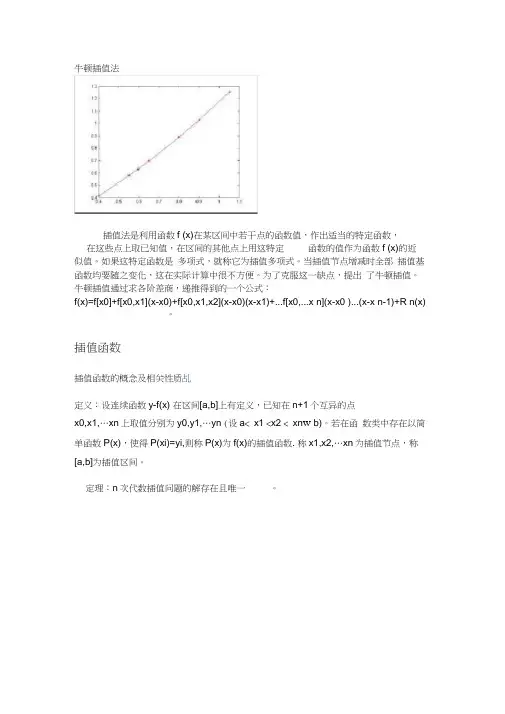
牛顿插值法插值法是利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
如果这特定函数是多项式，就称它为插值多项式。
当插值节点增减时全部插值基函数均要随之变化，这在实际计算中很不方便。
为了克服这一缺点，提出了牛顿插值。
牛顿插值通过求各阶差商，递推得到的一个公式：f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...x n](x-x0 )...(x-x n-1)+R n(x)。
插值函数插值函数的概念及相关性质乩定义：设连续函数y-f(x) 在区间[a,b]上有定义，已知在n+1个互异的点x0,x1,…xn上取值分别为y0,y1,…yn (设a< x1 <x2 < xn w b)。
若在函数类中存在以简单函数P(x)，使得P(xi)=yi,则称P(x)为f(x)的插值函数. 称x1,x2,…xn为插值节点，称[a,b]为插值区间。
定理：n次代数插值问题的解存在且唯一。
牛顿插值法C程序1,-Mt Cll. nilI frT-r-1■■』zJr1程序框图#include<stdio.h> void mai n(){float x[11],y[11][11],xx,temp, newto n;int i,j, n;printf("Newton 插值:\n请输入要运算的值:x=");sca nf("%f", &xx);printf(" 请输入插值的次数(n<11):n=");sca nf("%d",&n);printf("请输入％d组值:\n",n+1);for(i=0;i< n+1;i++){ prin tf("x%d=",i);sca nf("%f", &x[i]);prin tf("y%d=",i);sca nf("%f", &y[0][i]);XO=OMHUOW ①匚LHdlu9a巨A-」WL-qx-mxgD-mL'M-nKL'MHmuM①(LAW7 (++rL+uvrHD 」04 (+土=+u v ~ud 」04a -=x① s a)O O H(匚L o_(x )l l o)u ①-H u((A)£6U2H H(X )£6U①一)七】siuAs(oxsx)uoweN H 4 u o l o u a性胆 qewlAIw迴B犀<eo w① u-xx-=u\J6&Ha寸& )M灭<撫旨e ^=)匕 £」d宀CL l u ①&=二A +uo g ① u H u og ① u二 L.'vxxhdlu 晋 dlu2 〉(+土=+u v ~U_)」O 4disp('x 和y 的维数不相等！');return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f); % 将插值多项式展开f = vpa(f, 6);endend牛顿插值法摘要：值法利用函数f (x) 在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f(X)的近似值。
第8讲 牛顿插值公式§1.4 差商与差分及其性质 1 差商的概念:称10110)()(],[x x x f x f x x f --=为函数f (x )的一阶差商；称21021210],[],[],,[x x x x f x x f x x x f --=为函数f (x )的二阶差商；一般地，称010110],...,[],...,[],...,,[x x x x f x x f x x x f n n n n --=-为函数f (x )的n 阶差商；特别地，定义)(][00x f x f =为函数f (x )关于x o 的零阶差商。
由此可知，高阶差商总是由比它低一阶的的两个差商组合而成。
2（a ）n 阶差商可以表示成n +1个函数值01,,,n y y y 的线性组合,即∑-----==+-ki n i i i i i i i i k x x x x x x x x x x x f x x f 011100)())(())(()(],...,[该性质说明：k 阶差商],...,,[10n x x x f 计算是由函数值f (x 0),f (x 1),…f (x k )线性组合而。
如:],,[],,[],,[012201210x x x f x x x f x x x f ==；011100010110)()()()(],[x x x f x x x f x x x f x f x x f -+-=--=))(()())(()())(()()()()()()()()()()()(],[],[],,[120222101120100021221210111000111000201011212021021210x x x x x f x x x x x f x x x x x f x x x x x f x x x f x x x f x x x f x x x f x x x f x x x x x f x f x x x f x f x x x x f x x f x x x f --+--+--=--+------=-+-=------=--=对称性): 差商与节点的顺序无关。
即0110[,][,]f x x f x x =，012102021[,,][,,][,,]f x x x f x x x f x x x ==这一点可以从性质1看出。
3 利用差商表计算差商利用差商的递推定义,可以用递推来计算差商。
4 差分的概念定义设函数y=f (x )在等距节点),,1,0(0n i ih x x i =+=上的函数值f (x i )=f i ,其中，h 为常数称作步长。
称△f i =f i+1-f i ▽f i =f i -f i-1δf i =f (x i +h /2)-f (x i -h /2)=2121-+-i i ff分别为f (x )在i x处以h 为步长的一阶向前差分，一阶向后差分和一阶中心差分。
称符号△、▽、δ分别为向前差分算子，向后差分算子和中心差分算子。
⎪⎪⎩⎪⎪⎨⎧-=∇-∇=∇∆-∆=∆-+-+211-n 211-n n 11-n 1-n n 1-n 11-n n i i i i i i i i i ff f f f f f f f δδδ 在节点等距情况下，差商可用差分表示，设步长i i x x h -=+1，有 i i i i i i i y hx x x f x f x x f ∆=--=+++1)()(),(111i i i i i i i i i i i i y hy y h x x x x f x x f x x x f 221221212121)(21),(),(),,(∆=∆-∆=--=+++++++一般形式(数学归纳法可证)i kk k i i i y h k x x x f ∆=++!1),...,,(1§1.5 牛顿插值公式1. 牛顿插值公式的构造Lagrange 插值虽然易算，但若要增加一个节点时，全部基函数 l i (x ) 都需重新算过。
本节介绍另外一种方法-牛顿插值法，并用它解决上面所述问题。
由线性插值)()(0010101x x x x y y y x N ---+=，令)()(,,01010101100x x a a x N x x y y a y a -+=--== 二次插值能否写成))(()()(1020102x x x x a x x a a x N --+-+=由条件222112002)(,)(,)(y x N y x N y x N ===得120101020220101100,,x x x x y y x x y y a x x y y a y a ------=--== 推广得))...((...))(()()(10102010---++--+-+=n n n x x x x a x x x x a x x a a x N ,其中，n a a a ,,,10 为待定系数。
如何求n a a a ,,,10 ?解: 因为000()()[,]f x f x f x x x x -=-,所以000()()[,]()f x f x f x x x x =+-(0)又001011[,][,][,,]f x x f x x f x x x x x -=-,有001011[,][,][,,]()f x x f x x f x x x x x =+- (1)又010120122[,,][,,][,,,]f x x x f x x x f x x x x x x -=-010120122[,,][,,][,,,]()f x x x f x x x f x x x x x x =+- (2)一般地,nn n n x x x x x f x x x x f x x x x f --=-],...,,[],...,,,[],...,,,[1011010)](,...,,,[],...,,[],...,,,[1010110n n n n x x x x x x f x x x f x x x x f -+=- (n)将式(n)代入式(n-1), ...,式(2)代入式 (1),式(1)代入式 (0), 如此可得:0010()()[,]()f x f x f x x x x =+-01201[,,]()()f x x x x x x x +--+01011[,,,]()()()n n f x x x x x x x x x -+--- 0101[,,,,]()()()n n f x x x x x x x x x x +---尤为注意的是：最后一项中,差商部分含有x ,乃是余项部分,记作()n R x ;而前面n +1项中,差商部分都不含有x ,因而前面n +1项是关于x 的n 次多项式,记作()n N x ,这就是牛顿插值公式。
2 算例例1:当n=1时，0010()()[,]()f x f x f x x x x =+-0101[,,]()()f x x x x x x x +--,其中,10010()()[,]()N x f x f x x x x =+-010001()y y y x x x x -=+--。
这就是牛顿一次插值多项式，也就是点斜式直线方程。
当n=2时,0010()()[,]()f x f x f x x x x =+-01201[,,]()()f x x x x x x x +--012012[,,,]()()()f x x x x x x x x x x +---20010()()[,]()N x f x f x x x x =+-01201[,,]()()f x x x x x x x +--这就是牛顿二次插值多项式。
显然,200()()N x f x =,0121010101()()()()()()f x f x N x f x x x f x x x -=+-=-012202001()()()()()f x f x N x f x x x x x -=+--01122021020112()()()()1()()f x f x f x f x x x x x x x x x x x ⎛⎫--+--- ⎪---⎝⎭2()f x =。
即2()N x 满足二次插值条件。
0()0f x =,01[,]1f x x =,012[,,]4f x x x =,0123[,,,] 1.25f x x x x =-;则牛顿三次插值多项式为3()0(1)4(1)(3)N x x x x =+-+⨯--1.25(1)(3)(4)x x x -⨯---。
1 拉格朗日插值与牛顿插值的比较(1)()n P x 和()n N x 均是n 次多项式, 且均满足插值条件:()()(), 0,1,,n k n k k P x N x f x k n===。
由多项式的唯一性,()()n n P x N x ≡,因而,两个公式的余项是相等的,即(1)01()[,,,]()()(1)!n n n n f f x x x x x x n ξωω+=+(2)当插值多项式从n-1次增加到n 次时,拉格朗日型插值必须重新计算所有的基本插值多项式;而对于牛顿型插值,只需用表格再计算一个n 阶差商,然后加上一项即可。
4 等距牛顿插值公式 插值节点为等距节点：0k x x kh =+，0,1,,k n =,如下图：h h h ... h牛顿插值公式 设等距节点0k x x kh=+，记(),0,1,,k k y f x k n ==.当0[,]n x x x ∈，令0x x th =+，0t n ≤≤. 例如（下图）123x 在x 2，x 3的中点时，0 2.5x x h=+。
将牛顿插值公式中的差商用差分代替,而00()()(),k x x x th x kh t k h -=+-+=-从而,牛顿插值公式在等距插值节点下的形式为:00()n N x y t y =+∆+32000111(1)(2)(1)(1)(1)3!!2!n t t t y t t t n y t t y n +--∆++--+∆-∆余项为(1)(1)11()()()(1)!(1)!n n R x f x f n n n n ξω++==++1()(1)()n h t t t n ξ+-- 这是等距牛顿向前插值公式。
例4: 设()xy f x e ==插值节点为1,1.5,2,2.5,3x =,相应的函数值如下表,求f (2.2)。
此时[x k , x k+1],x =2.2=1+2.4h 故t=2.4,于是2200018.87232(2.2)(1)2!N y t y t t y ==+∆+-∆求3(2.2)N 时，在(.)2N 22后加一项：13(1)(2)03!t t t y--∆ ,12.4(2.41)(2.42)0.742100.166236=⨯⨯-⨯-⨯=，所以32(2.2)(2.2)0.166239.03855N N =+=求4(2.2)N 时，在3(2.2)N 后再加一项：401(1)(2)(3)4!t t t t y ---∆ 12.4(2.41)(2.42)(2.43)0.4814624=⨯⨯-⨯-⨯-⨯0.01618=-，所以43(2.2)(2.2)0.016189.02237N N =-=2320.15269 , 0.01354 , 0.00264R R R ==-=。
