扭转刚度计算.

箱形截面扭转刚度计算公式全文共四篇示例，供读者参考第一篇示例：箱形截面扭转刚度是指箱形截面在受扭作用下抵抗形变的能力，是结构工程中重要的性能指标之一。

在工程设计中，经常需要计算箱形截面的扭转刚度，以保证结构的稳定性和安全性。

本文将重点介绍箱形截面扭转刚度的计算公式及其应用。

一、箱形截面扭转刚度的定义箱形截面扭转刚度是指箱形截面在扭转作用下所抵抗的形变能力，通常用符号G表示。

在箱形截面中，扭转刚度主要由箱形截面的截面尺寸和材料的弹性模量等因素决定。

扭转刚度越大，表示箱形截面在扭转作用下的抵抗能力越强。

对于矩形截面的箱形截面，其扭转刚度可以通过以下公式计算：G = (bh^3)/3G表示箱形截面的扭转刚度，b表示箱形截面的宽度，h表示箱形截面的高度。

对于更复杂的箱形截面，可以通过适当简化模型，根据不同截面形状和尺寸，灵活选择不同的计算公式进行计算。

1. 结构设计中的应用：在结构设计中，常常需要对箱形截面的扭转刚度进行计算，以保证结构在扭转荷载作用下的稳定性和安全性。

根据箱形截面的扭转刚度计算结果，可以选择适当的截面尺寸和材料，进行结构设计和优化。

箱形截面的扭转刚度是一个重要的结构性能参数，对于结构的设计、分析和施工具有重要意义。

希望本文介绍的箱形截面扭转刚度的计算公式及其应用能够对相关领域的工程师和研究人员有所帮助，推动结构工程的发展和进步。

【End】第二篇示例：箱形截面扭转刚度是指材料在受到扭转力作用下，抵抗其扭转变形的能力。

在工程设计和结构分析中，掌握箱形截面扭转刚度的计算公式是十分重要的。

箱形截面是指由长方形梁和薄壁平板构成的截面形式，广泛应用于建筑结构和机械设备中。

在计算箱形截面扭转刚度时，需要考虑箱形梁的截面尺寸、材料性质以及扭转力的作用位置等因素。

箱形截面扭转刚度的计算公式可以通过结构力学和钢结构设计的理论推导得出。

首先，我们需要明确箱形梁的截面尺寸及材料性质。

假设箱形梁的截面尺寸为宽度为b，高度为h，厚度为t，材料的弹性模量为E，剪切模量为G。

12.3 扭转杆件的强度、刚度计算对受扭转的杆件，除了强度要求外，通常刚度也要同时考虑。

受扭杆件危险点均为纯剪切应力状态。

对纯剪切应力状态，可以证明，与第一强度理论对应的强度条件为≤（12-4）与第三、四强度理论对应的强度条件为≤（12-5）≤（12-6）式中，[τ]为许用切应力，它与许用正应力之间的关系为脆性材料[ τ ] = （0.8 ~ 1）[ σ ]塑性材料[ τ ] = （0.5 ~ 0.6）[ σ ]例12-4一钢传动轴如图12-4a所示，转速n = 208rpm，主动轮B的输入功率P=6kW，两个从动轮A、CB的输出功率分别为P A = 4kW，P c = 2kW。

已知：轴的许用应力[σ] = 60MPa，许用单位扭转角[ϕ]=1︒/m，切变模量G = 80GPa，试设计轴的直径d。

解：1．计算外力偶矩，绘扭矩图。

用截面法及扭矩符号的规定，得AB、BC段的扭矩分别为T AB = 183.6N·mT BC = -91.8N·m根据以上计算结果，作扭矩图如图12-4b所示2．按强度条件设计轴的直径由扭矩图可见，最大扭矩为T max = 183.6N·m，危险截面为AB段各横截面。

危险点在危险截面上周边各个点，处于纯剪切应力状态。

根据最大切应力理论，强度条件应为≤≤得 d ≥3．按刚度条件设计轴的直径由刚度条件式（12-2），扭转刚度条件为ϕmax = ≤[ ϕ]≤[ϕ]得d≥为了同时满足强度及刚度要求，应在以上两计算结果中取较大值作为轴的直径，即轴的直径应大于或等于34mm，可取d = 34mm。

例12-5实心圆轴横截面上的扭矩T = 5kN·m。

轴的许用应力[ ] = 87MPa，试按强度设计轴的直径D。

若将轴改为空心圆轴，且内外直径之比，试设计截面尺寸。

并比较实心圆轴和空心圆轴所需的材料用量。

解：本题按第四强度理论来设计。

对实心愿轴，由强度条件式（12-6）≤即≤得D≥取D = 80mm。

双膜片联轴器静态扭转刚度
双膜片联轴器是由两片膜片和两个半联轴器组成，膜片又由若干个单膜片与波形环、连接环和夹紧螺栓等元件组成。

对于双膜片联轴器的静态扭转刚度，首先需要明确的是，其刚度主要取决于螺栓的预紧力、膜片的刚度、螺栓与膜片的连接刚度以及螺栓的抗剪切刚度等因素。

在理论上，当考虑螺栓预紧力、膜片刚度和螺栓与膜片连接刚度时，双膜片联轴器的静态扭转刚度可以通过下面的公式进行计算：
K=Kb(1+αm+βm)
其中，K为静态扭转刚度，Kb为螺栓预紧力产生的刚度，αm为膜片刚度与螺栓抗弯刚度的比值，βm为螺栓与膜片连接刚度与膜片刚度的比值。

然而，由于在实际工况中，可能存在各种不确定因素和动态效应，因此计算结果可能与实际值存在一定的偏差。

因此，对于具体的扭转刚度数值，建议通过实验的方式进行测量。

此外，值得注意的是，双膜片联轴器的设计需要特别考虑其动平衡和阻尼特性等因素，以确保其在实际应用中的稳定性和可靠性。

以上内容仅供参考，如需更多信息，建议查阅双膜片联轴器相关文献或咨询机械工程专家。

方管计算公式表方管（也称为方钢管）是一种常见的钢管材料，广泛应用于建筑、机械制造等领域。

在使用方管进行设计和计算时，掌握一些基本的计算公式是非常重要的。

本文将为您介绍方管常用的计算公式，帮助您更好地应用方管。

一、截面面积计算公式方管的截面面积是一个重要的物理量，它用来描述方管的横截面积大小。

根据方管的尺寸，我们可以使用如下公式计算方管的截面面积：截面面积 = 边长1 ×边长2其中，边长1和边长2分别表示方管的两条边的长度。

通过测量方管的尺寸，将其代入上述公式，即可得到方管的截面面积。

二、体积计算公式方管的体积是指方管所占据的空间大小，用来描述方管的容积。

根据方管的尺寸，我们可以使用如下公式计算方管的体积：体积 = 长度 ×截面面积其中，长度表示方管的长度，截面面积表示方管的截面面积。

通过测量方管的尺寸，并代入上述公式，即可计算出方管的体积。

三、弯曲应力计算公式在使用方管进行弯曲时，方管会受到一定的弯曲应力。

为了确保方管在弯曲过程中不发生破裂或变形，我们需要计算弯曲应力。

根据方管的尺寸和力学性质，我们可以使用如下公式计算方管的弯曲应力：弯曲应力 = (M × y) / (W × I)其中，M表示弯曲力矩，y表示截面离中性轴的距离，W表示截面模量，I表示截面惯性矩。

通过确定方管的尺寸和力学性质，并代入上述公式，即可计算出方管的弯曲应力。

四、拉伸应力计算公式在拉伸过程中，方管会受到拉伸应力的作用。

为了确保方管在拉伸过程中不发生破裂或变形，我们需要计算拉伸应力。

根据方管的尺寸和力学性质，我们可以使用如下公式计算方管的拉伸应力：拉伸应力 = F / A其中，F表示拉伸力，A表示截面积。

通过确定方管的尺寸和力学性质，并代入上述公式，即可计算出方管的拉伸应力。

五、扭转刚度计算公式在方管进行扭转时，方管会受到一定的扭矩和扭转角度的作用。

为了计算方管的扭转刚度，我们可以使用如下公式：扭转刚度 = (G × J) / L其中，G表示剪切模量，J表示截面扭转常量，L表示方管的长度。

工字钢刚度计算公式(一)工字钢刚度计算公式1. 弹性刚度计算公式•工字钢的弹性刚度可以根据以下公式计算：K = E * A / L其中，K表示弹性刚度，E表示材料的弹性模量，A 表示截面的面积，L表示工字钢的长度。

例如：假设工字钢的弹性模量为200 GPa，截面面积为500 cm^2，长度为5 m，则工字钢的弹性刚度为：K = 200 GPa * 500 cm^2 / 5 m = 20 Nm^22. 弯曲刚度计算公式•工字钢的弯曲刚度可以根据以下公式计算：K = E * I / L^3其中，K表示弯曲刚度，E表示材料的弹性模量，I 表示工字钢截面的惯性矩，L表示工字钢的长度。

例如：假设工字钢的弹性模量为200 GPa，截面的惯性矩为500 cm^4，长度为5 m，则工字钢的弯曲刚度为：K = 200 GPa * 500 cm^4 / (5 m)^3 = Nm^23. 扭转刚度计算公式•工字钢的扭转刚度可以根据以下公式计算：K = G * J / L其中，K表示扭转刚度，G表示材料的剪切模量，J 表示工字钢截面的极惯性矩，L表示工字钢的长度。

例如：假设工字钢的剪切模量为80 GPa，截面的极惯性矩为200 cm^4，长度为5 m，则工字钢的扭转刚度为：K = 80 GPa * 200 cm^4 / 5 m = Nm^24. 总刚度计算公式•工字钢的总刚度可以根据以下公式计算：K_total = K_elastic + K_bending + K_torsion其中，K_total表示总刚度，K_elastic表示弹性刚度，K_bending表示弯曲刚度，K_torsion表示扭转刚度。

例如：假设工字钢的弹性刚度为20 Nm^2，弯曲刚度为 Nm^2，扭转刚度为 Nm^2，则工字钢的总刚度为：K_total = 20 Nm^2 + Nm^2 + Nm^2 = Nm^2 以上为工字钢刚度计算的相关公式及其解释。

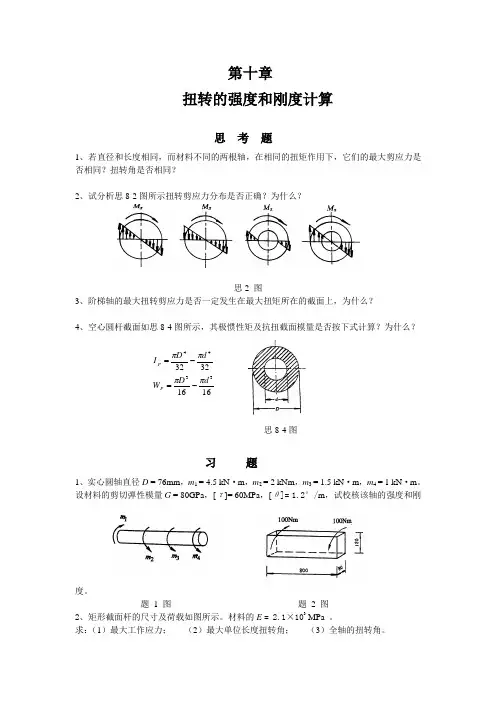
第十章扭转的强度和刚度计算思 考 题1、若直径和长度相同，而材料不同的两根轴，在相同的扭矩作用下，它们的最大剪应力是否相同？扭转角是否相同？2、试分析思8-2图所示扭转剪应力分布是否正确？为什么？思2 图3、阶梯轴的最大扭转剪应力是否一定发生在最大扭矩所在的截面上，为什么？4、空心圆杆截面如思8-4图所示，其极惯性矩及抗扭截面模量是否按下式计算？为什么？思8-4图习 题1、实心圆轴直径D = 76mm ，m 1 = 4.5 kN ·m ，m 2 = 2 kNm ，m 3 = 1.5 kN ·m ，m 4 = 1 kN ·m 。

设材料的剪切弹性模量G = 80GPa ，[τ]= 60MPa ，[θ]= 1.2°/m ，试校核该轴的强度和刚度。

题 1 图 题 2 图2、矩形截面杆的尺寸及荷载如图所示。

材料的E = 2.1×103 MPa 。

求：（1）最大工作应力； （2）最大单位长度扭转角； （3）全轴的扭转角。

161632323344d D W d D I P P ππππ-=-=3、图示一联接水轮机与发电机的实心圆轴 。

已知轴横截面的直径为650 mm ，长度为6000 mm ，水轮机的功率P = 10000 PS ，钢材的剪切弹性模量G = 79 GPa 。

问当水轮机的转速n = 57.7r/min 时,轴内的最大剪应力和轴两端的相对扭转角各为多大?4、有一受扭钢轴，已知其横截面直径d = 25 m m ，剪切弹性模量 G = 79 GPa ，当扭转角为6°时的最大剪应力为95 MPa ，试求此轴的长度。

习题答案：1. =max τ58.1Mpa2. =max τ0.56 Mpa0151.0max =ϑrad/m 3. =max τ22.6 Mpaϕ=0.302° 4. l =2.18m。