数列的极限

数列极限的定义与性质数列是由一系列按特定规律排列的数字组成的序列。

在数学中，了解数列的极限是非常重要的。

通过研究数列的极限，我们可以揭示数列的性质，并且可以应用到不同的领域中。

本文将探讨数列极限的定义与性质，帮助读者更好地理解和应用数列。

一、极限的定义数列的极限是指当数列中的项趋近于某个值时，数列的值也趋近于该值。

数列极限可以用以下方式进行定义：设有数列 {a_n}，其中 n 表示数列中的项的索引（在数列中的位置）。

若对于任意给定的正实数ε，都存在正整数 N，使得当 n > N 时，有|a_n - A| < ε 成立，则称数列 {a_n} 的极限为 A，记作lim(n→∞) a_n = A。

其中，|a_n - A| 表示 a_n 与 A 之间的差的绝对值。

ε (epsilon) 是一个任意小的正实数，N 是一个正整数。

二、极限的性质数列极限具有以下性质：1. 极限的唯一性：设数列 {a_n} 的极限为 A，则数列的极限是唯一的，即不存在另外的极限值。

2. 极限的有界性：若数列 {a_n} 的极限为 A，则对于任意给定的正实数ε，存在正整数 N，使得当 n > N 时，有|a_n| < |A|+ε 成立。

换句话说，当 n 足够大时，数列的值都在 A 的某个邻域内。

3. 极限的保号性：若数列 {a_n} 的极限为 A，且 A > 0 (或 A < 0)，则存在正整数 N，使得当 n > N 时，有 a_n > 0 (或 a_n < 0) 成立。

也就是说，当 n 足够大时，数列的值与其极限符号一致。

4. 极限的四则运算：设数列 {a_n} 和 {b_n} 的极限分别为 A 和 B，则有以下四则运算定理：- 两个数列的和的极限等于两个数列的极限的和，即lim(n→∞) (a_n + b_n) = A + B。

- 两个数列的差的极限等于两个数列的极限的差，即lim(n→∞) (a_n - b_n) = A - B。

数列极限方法一、引言数列极限是数学分析中的一个基本概念，它描述了一个数列当项数趋于无穷时的行为。

理解数列极限的概念是深入理解数学分析和其他数学领域的基础。

本文将介绍几种常用的数列极限的求解方法。

二、数列极限的基本概念一个数列 {an} 的极限定义为：对于任意小的正数ε，都存在一个正整数 N，使得当 n > N 时，|an - L| < ε恒成立，其中 L 为常数。

我们记作 lim(n→∞) an = L。

三、求解数列极限的方法1.直接观察法：对于一些简单的数列，我们可以通过观察它们的规律来直接得出极限。

例如，对于数列 {1, 1/2, 1/3, 1/4, ...}，显然有 lim(n→∞) 1/n = 0。

2.夹逼法：对于一个数列 {an}，如果存在两个常数 M 和 m，使得 m ≤ an ≤M 对于所有的 n 都成立，那么 lim(n→∞) an = M（或 lim(n→∞) an = m）。

这是因为对于任意的ε > 0，存在一个 N，使得当 n > N 时，M - ε≤ an ≤M + ε。

由于 m ≤ an ≤ M，我们可以得到 |an - M| < ε，即 lim(n→∞) an = M。

3.收敛的级数法：如果一个级数Σan 收敛到 S，那么其部分和 Sn 必定趋近于S。

因此，对于任何的 n，我们有 lim(n→∞) Sn = S。

特别地，如果级数的每一项都非负（或都非正），且级数收敛，那么该数列必定有界且单调。

4.洛必达法则：洛必达法则是求解极限的一种有效方法，特别适用于0/0型和∞/∞型的极限问题。

如果 f 和 g 在某点 a 的某邻域内可导，且 g' (a)≠0，那么 lim(x→a) f'(x)/g'(x) = f'(a)/g'(a)。

在数列的情境下，这可以被应用于求和公式的展开。

5.斯特林公式：斯特林公式给出了一个非负整数 n 的正整数次幂的阶乘与 n!的近似比。

数列极限的知识点总结一、数列极限的定义1.1 数列首先要了解数列的概念。

数列是由一系列按照一定顺序排列的数所组成的有序集合。

数列通常用符号{an}表示，其中an代表数列的第n个元素。

数列是数学中一种基本的数学概念，它在许多数学问题中都起着重要的作用。

1.2 数列极限接着要了解数列的极限。

数列{an}的极限是指当n趋向于无穷大时，数列中的元素an的值趋近于一个常数L，即lim(an) = L。

如果这样一个数L存在，那么我们就说数列{an}收敛，并且把L称为数列的极限，记作lim(an) = L。

如果这样一个数L不存在，那么我们就说数列{an}发散。

1.3 数列极限的形式化定义对于给定的数ε，如果存在一个正整数N，使得当n大于N时，|an - L| < ε恒成立，那么称L是数列{an}的极限。

这样的N存在的话，就称这N是数L和ε的函数。

1.4 无穷大数列如果数列{an}中的元素an当n趋向于无穷大时，它的绝对值|an|趋向于无穷大，那么就称数列{an}是无穷大的。

对于无穷大数列，我们通常用符号lim(an) = ±∞来表示。

1.5 注意事项在讨论数列极限的问题时，需要注意以下几点：1) 数列的极限可能是一个有限的常数，也可能是无穷大。

2) 一般来说，数列的极限不一定存在，也可能有多个极限（一般在不同n的取值范围内）。

3) 要特别注意当n趋于无穷大时，数列中的元素an的绝对值的行为，关系到数列是否是无穷大数列。

以上是数列极限的基本概念和定义，下面我们将介绍数列极限的相关性质。

二、数列极限的相关性质2.1 唯一性如果数列{an}收敛，那么它的极限是唯一的。

换句话说，如果lim(an) = L1和lim(an) = L2，那么L1 = L2。

2.2 有界性如果数列{an}收敛，那么它一定是有界的，即存在一个正实数M，使得|an| < M（n∈N）。

2.3 保号性如果数列{an}收敛到一个有限的极限L，那么当n充分大时，数列{an}的元素和L有相同的正负号。

数列极限的运算法则
数列是由一系列数字按照一定规律排列而成的序列，而数列的极限是指当数列中的项无限接近某个特定值时，该特定值就是该数列的极限。

数列的极限可以通过一些运算法则来求解，这些运算法则包括以下几个方面。

1. 线性运算法则：如果数列{an}和{bn}的极限分别为A和B，那么对于任意
实数c，数列{can}的极限为cA，数列{an+bn}的极限为A+B，数列{an-bn}的极限
为A-B。

2. 乘法运算法则：如果数列{an}和{bn}的极限分别为A和B，那么数列{anbn}的极限为AB。

3. 除法运算法则：如果数列{an}和{bn}的极限分别为A和B，且B不等于0，那么数列{an/bn}的极限为A/B。

4. 幂运算法则：如果数列{an}的极限为A，且m是一个正整数，那么数列{an^m}的极限为A^m。

5. 复合函数运算法则：如果函数f(x)在x=A处连续，并且数列{an}的极限为A，那么数列{f(an)}的极限为f(A)。

6. 夹逼准则：如果数列{an}，{bn}和{cn}满足an≤bn≤cn，并且数列{an}和{cn}的极限都为A，那么数列{bn}的极限也为A。

7. 极限的唯一性：如果数列{an}的极限存在，那么该极限是唯一的。

这些运算法则可以帮助我们计算数列的极限，使得我们能够更加方便地求解数列的极限问题。

但需要注意的是，这些运算法则只适用于满足一定条件的数列，例如乘法运算法则中要求乘积数列的每一项都存在，除法运算法则中要求除数数列的每一项都不为0等。

在应用运算法则时，我们需要仔细分析数列的性质，确保运算的合理性。

数列极限及其应用数列是数学中重要的概念之一，数列极限是数学分析中的重要内容。

在本文中，我们将探讨数列极限的定义、性质以及其在数学和现实生活中的应用。

一、数列极限的定义和性质数列是由一系列按照一定规律排列的数字组成的序列。

数列通常表示为{a₁,a₂, a₃, ......, aₙ}，其中a₁、a₂、a₃等是数列中的项。

数列的极限是指当n趋向于无穷大时，数列中的项趋近于确定的常数L。

这一定义可以表示为：lim{n→∞} aₙ = L数列极限的性质包括：1. 唯一性：数列的极限只有唯一的值。

2. 有界性：若数列存在极限，则数列必定有界，即存在上界和下界。

3. 保号性：若数列存在极限且其极限为正（或负）数，则数列从某项起，总是正（或负）号。

4. 夹挤性：若数列的每项均位于两个收敛数列的中间，则该数列也是收敛的，并有相同的极限。

二、数列极限的应用1. 数学分析中的应用：数列极限在微积分中有着重要的应用。

利用数列极限的概念，我们可以定义导数和积分，并研究函数的连续性和各种变化规律。

数列极限的概念是微积分的基础之一，它为我们理解和深入研究函数的性质提供了便利。

2. 数列极限在无穷级数求和中的应用：无穷级数是由无穷个项按照一定规律排列而成的数列。

利用数列极限的概念，我们可以判断无穷级数是否收敛，以及求出其和。

例如，经典的几何级数可以通过数列极限的方法求和，从而得到其和为有理数的结论。

3. 数列极限在金融投资中的应用：在金融投资中，数列极限可以用于计算投资回报率。

通过考察投资金额随时间增长的趋势，我们可以得到不同投资方案的回报率，并作出合理的投资决策。

4. 数列极限在物理学中的应用：在物理学中，数列极限可以用于描述物体运动的速度和加速度。

例如，通过分析质点在无穷小时间间隔内的位移变化，我们可以定义速度和加速度，并利用数列极限的概念来研究物体的运动轨迹和变化规律。

5. 数列极限在市场预测中的应用：数列极限可以用于分析市场行情和预测未来的趋势。

数列极限的解释
在数学中，数列极限是一种重要的概念，用来描述数列中的值如何无限接近某个特定的值。

数列是由一系列按照特定顺序排列的数所组成的列表。

数列极限的定义是：对于给定的数列，如果随着数列项的无限增多，数列中的值趋近于一个特定的值，我们就说这个特定的值是该数列的极限。

可以将这种趋近视为无限接近特定值的过程。

通常，数列的极限可以通过数学表达式或符号来表示。

当我们说数列{1，1/2，1/3，1/4，...}的极限为0时，可以用数学符号表示为lim(1/n) = 0，其中lim代表极限，n代表数列的索引。

数列极限的概念有助于我们研究数列中的趋势和性质。

在数学和应用领域中，数列极限的研究具有重要的意义。

它可以帮助我们预测数列的未来行为，解决各种实际问题，以及推导出其他数学定理。

数列极限的理解与实际生活中一些有趣的现象相似，当我们不断增加一个球的弹跳次数时，每一次弹跳的高度都会趋近于某个极限值。

这个极限值可以被视为数列的极限。

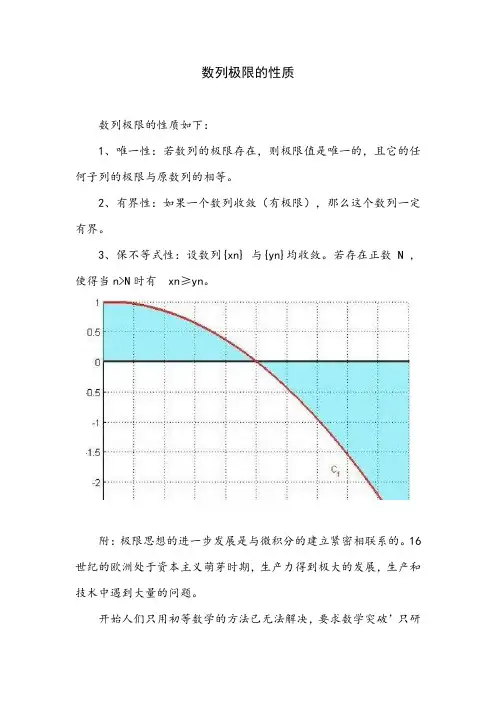
数列极限的性质
数列极限的性质如下：
1、唯一性：若数列的极限存在，则极限值是唯一的，且它的任何子列的极限与原数列的相等。

2、有界性：如果一个数列收敛（有极限），那么这个数列一定有界。

3、保不等式性：设数列{xn} 与{yn}均收敛。

若存在正数N ，使得当n>N时有 xn≥yn。

附：极限思想的进一步发展是与微积分的建立紧密相联系的。

16世纪的欧洲处于资本主义萌芽时期，生产力得到极大的发展，生产和技术中遇到大量的问题。

开始人们只用初等数学的方法已无法解决，要求数学突破’只研
究常量‘的传统范围，而寻找能够提供能描述和研究运动、变化过程的新工具，是促进’极限‘思维发展、建立微积分的社会背景。

起初牛顿和莱布尼茨以无穷小概念为基础建立了微积分，后来因遇到逻辑困难，所以在他们的晚期都不同程度地接受了极限思想。

数列极限存在的条件
1. 数列极限的定义：
数列极限是指当一组数的k项的取值趋向于一个值时，此数列的k项称为极限值。

2. 数列极限存在的条件：
(1) 数列项具有确定的规律性：求极限必须有一个已知的数列，该数列必须具有一个确定的规律性或者说，必须是数系。

(2) 导数存在：不存在极限的情况通常是由于数列函数无法在某一点求得它的导数，或者说导数为正无限大、负无限大或无穷大。

(3) 无穷多项式存在：无穷项数列的极限应存在，这样的函数往往可以简化为无穷多项式的形式。

(4) 左右极限存在：左右极限的存在是数列极限存在的充要条件，即对于任意一个数列，其任意一点处必须具有左右极限才能满足数列极限存在条件。

(5) 极限算法存在：若数列满足上述条件，那么就可以通过极限算法来计算极限的值。

(6) 原函数的准确性：在计算极限的值时，数列函数的准确性也非常重要，原函数需要能够准确的表达该数列的趋势。

数列的极限、数学归纳法、知识要点 (一) 数列的极限列中找到一项 aN,使得当n>N 时，|an-A|< 恒成立，则称常数 A 为数列｛a n ｝的极限，记作lim a n A .n2.运算法则：若lim a n 、lim b n 存在，则有lim(a n b n )lim a n lim ；lim( a n b n ) lim a n lim b nnnnnn na lim a nlim —— , (lim b n 0)nb n lim b n nn(a1)3.两种基本类型的极限<1> S= lima nn1(a 1)不存在(a诚a<2>设f (n)、g(n)分别是关于n 的一元多项式，次数分别是p 、q ，最高次项系数分别为 a p 、0 (p q)b p 且 g( n) 0(n N),则 limng(n )(二)数学归纳法①验证命题对于第一个自然数 n n 0成立。

②假设命题对 n=k(k > n o )时成立，证明n=k+1时命题也成立 则由①②，对于一切n > n o的自然数，命题都成立。

、例题(数学的极限)1.定义：对于无穷数列｛a n ｝，若存在一个常数 A,无论预选指定多么小的正数 ，都能在数 4.无穷递缩等比数列的所有项和公式：S「q E )无穷数列｛a n ｝的所有项和: a p- (p q) b q 不存在 (p q)S lim S n (当 lim S n 存在时)nn数学归纳法是证明与自然数 n 有关命题的一种常用方法，其证题步骤为:(4) lim( J-3Lnn 1 n 1(5) lim G. n 2 2n n)=;n例2 •将无限循环小数 0.12 ； 1.32 12 化为分数.『1例3•已知lim(an b) 1,求实数a, b 的值;nn 1例 4•数列{a n },{b n }满足 lim (2a n +b n )=1,lim (a n — 2tn)=1，试判断数列{a n },{b n }的极限是否nn存在，说明理由并求lim (a n b n )的值.n例5.设首项为a ，公差为d 的等差数列前-项的和为A,又首项为a,公比为r 的等比数列S例6.设首项为1,公比为q(q>0)的等比数列的前 -项之和为S n ,又设T n =— (n 1,2,L ),S- 1求 lim T n .n21 例7. ｛a n ｝的相邻两项a n ,a n+1是方程x —c -X +(—)n =0的两根，又a 1=2,求无穷等比C 1 ,c 2, (3)C n ,…的各项和.例8在半径为R 的圆内作内接正方形， 在这个正方形内作内切圆， 又在圆内作内接正方形,如此无限次地作下去，试分别求所有圆的面积总和与所有正方形的面积总和。